Abstract
Recently, high-order statistics have received more and more interest in the field of hyperspectral anomaly detection. However, most of the existing high-order statistics based anomaly detection methods require stepwise iterations since they are the direct applications of blind source separation. Moreover, these methods usually produce multiple detection maps rather than a single anomaly distribution image. In this study, we exploit the concept of coskewness tensor and propose a new anomaly detection method, which is called COSD (coskewness detector). COSD does not need iteration and can produce single detection map. The experiments based on both simulated and real hyperspectral data sets verify the effectiveness of our algorithm.
Similar content being viewed by others
Introduction
The research on the anomaly detection of hyperspectral data has drawn much attention recently in many fields1,2,3. The so-called anomaly detection is basically to find out “abnormal” pixels from an image where the targets and their associated background are both unknown. Many anomaly detection methods have been proposed, among which RX Detector (RXD)4,5,6 is the most typical one. It has been applied to both multi and hyper-spectral successfully in terms of anomaly detection. In fact, the expression of RXD is equivalent to the Mahalanobis distance. There are many anomaly detection operators derived from RXD, such as modified RX (MRX), normalized RX (NRX), weighted RX, Causal RX7 and adaptive causal anomaly detector algorithm (ACAD)8. The low probability detector (LPD)9 is another anomaly detector used frequently. LPD determines whether a pixel is abnormal or not according to the relationship between any pixel of the image and the unity vector multiplied by the inversion of the sample auto-correlation matrix. The uniform target detector (UTD) is an evolved version of LPD which has a translational shift of the origin of the image to the mean vector. Kwon10 proposed a new anomaly detection method, dual window-based eigen separation transform anomaly detector (DWEST). DWEST model involves two local windows, namely inner and outer windows, which are designed to maximize the separation between anomalies and background. The inner window is used to detect the anomalies presented in it, while the outer window is used to model the background of the anomalies. By moving these two local windows in an image, we can calculate the local mean and covariance matrix for each window and their differences. Consequently, anomalies can be extracted by projecting the differential mean between two windows onto the eigenvector associated with the largest positive eigenvalue of the differential covariance matrix. Similar to DWEST, nested spatial window-based target detector (NSWTD) is presented in11. NSWTD model involves three nested local windows, namely, inner, middle and outer windows. The first two windows are used to extract the smallest and largest anomalies respectively, while the outer window is used to model the local background. Moreover, the other key difference of this model from the DWEST and RX-based algorithms is to use the orthogonal projection divergence (OPD) instead of eigenvector projection or sample covariance matrix as a measurement. Based on a nonparametric model, the combined F-Test anomaly detector (CFT) is presented by Rosario12. The main assumption of this method has an asymptotic behavior of Fisher's F distribution for data sets which are examined by a common statistical test. Some other anomaly detection methods can be seen at13,14,15.
The anomaly detectors mentioned above are all basically conducted from the statistical perspective. The statistics used include first-order statistics (e.g., mean vector) and second-order statistics (e.g., covariance matrix). It is not sufficient to use the first-order and the second-order statistics since the distributions of scatter points in feature space for most real images are not normal distributions.
In this study, the third-order statistical tensor is introduced to extract anomalies. In fact, there are many approaches in existing literature for anomaly detection using high-order statistics16,17. However, all these approaches are the direct applications of the blind signal separation (BSS) methods (e.g., FastICA), which generally involve step-by-step iterations to reach the optimal solution. As a result, they are apt to be trapped in local minima. In order to address the convergence issue, Geng18 introduced the concept of coskewness tensor to hyperspectral data analysis and proposed a target detection method based on higher order singular value detection (HOSVD). Nevertheless, both the BSSS-based techniques and HOSVD are in the domain of feature extraction, aiming at the extraction of not only the anomalies but also the other independent components in the image.
In this paper, combining the concept of third-order statistical tensor and the idea of RXD, we present a new anomaly detection method termed coskewness tensor detector (COSD). The proposed method can directly get the distribution of the anomaly of a hyperspectral image without any iteration, which can therefore avoid problems of the BSS-based methods.
Results
Although there are many anomaly detection algorithms based on the 2nd-order statistic, they are all generally derived from RXD. Similarly, we can also derive corresponding algorithms based on COSD. Therefore, the experiments in this study only focus on comparing the performances between COSD, FastICA and RXD. In order to facilitate the comparison between COSD and FastICA, we used skewness as a measure of non-Gaussianity in FastICA. In addition, since FastICA can produce a lot of independent components, we just select the one with the greatest skewness as the detection result.
Evaluation with simulated data
The simulated image of two bands with 50 × 50 pixels was first used in this experiment. Simulation data consists of two parts, abnormal targets (8*8) and their background. The background pixels fit a Gaussian distribution. The target was located in the upper left corner of the image and randomly scattered outside the background in the feature space of the image (see Fig. 1).
The comparisons between RXD, FastICA and COSD are given in Fig. 2. By a visual comparative analysis, the performance of COSD is superior to that of RXD. Fig. 3 shows the receiver operating characteristic (ROC) curve of detection rate versus false alarm rate for the three algorithms (see reference [15] for their definitions of detection rate and false alarm rate). Clearly, the detection performance of COSD is comparable to that of FastICA and both are better than that of RXD.
Evaluation with real hyperspectral data
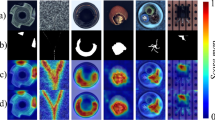
The hyperspectral data of 100*100 pixels from OMIS-II (Operational Modular Imaging Spectrometer) is used to test these methods. The hyperspectral imaging system was developed by Shanghai Institute of Technical Physic, Chinese Academy of Sciences (SITP). The data, which was acquired by the Aerial Photogrammetry and Remote Sensing Bureau in Xi'an, China in 2003, includes 64 bands from visible to thermal infrared with 3.6 m spatial resolution and 10 nm spectral resolution in the visible and near infrared region (60 bands). There were small man-made targets simulated as common objects within the scene, which were distributed at two locations around the top right corner of the image (marked by the rectangles in Fig. 4 a), consisting of tens of pixels. From the true color (approximately) composition image (see Fig. 4 a), it is hard to find any information of the targets in the rectangles.
From Fig. 4b, we can see two small bright blocks at the top right corner, which are the man-made targets. It indicates that RXD can distinguish them as the abnormal pixels from the background. Fig. 4c is the result of COSD, where the two man-made targets are highlighted significantly as the abnormal pixels while the rest is greatly suppressed as the background. The result of NCOSD in Fig. 4d indicates that it is good enough to extract anomalies by only using the skewness information. Fig. 5 shows the ROC (receiver operating characteristic) curve of detection rate versus the false alarm rate for both RXD and COSD. It illustrates that the detection capability of COSD has a significant advantage over that of RXD.
Now we turn to the comparison between FastICA and COSD. Usually, FastICA gets all the independent components through iterations and the one with the maximum skewness is chosen as the anomaly detection result. However, due to the local optimum, the first independent component of FastICA is not always corresponding to the global maximum skewness, thus different surface objects may be detected (see Fig. 6, which shows the inconsistency of anomaly detections. Besides, the skewness-based FastICA does not have a global convergence. Nevertheless, our COSD does not have these problems.
Discussion
In this study we proposed a new method of using high-order statistic tensor to detect the anomaly of a hyperspectral image and analyzed in detail the application of the skewness tensor in the anomaly detection. Compared to the traditional methods based on the second-order statistics, COSD has a better capacity to extract the abnormal objects. Moreover, COSD can directly get the distribution of the abnormal objects by using a higher-order statistic tensor, compared to the traditional methods based on blind signal separation methods. Since COSD does not need iteration, it can avoid the shortcomings of the blind signal separation methods. By the experiment with simulated data, it shows that the detection performance of the COSD is better than that of RXD. In the experiment using real hyperspectral data, it is illustrated that the COSD can highlight the man-made targets as the anomalies out of the image successfully. It is noteworthy that, the obtained abnormal pixels might not be the ones of interest due to the uncertainty of the abnormal pixels in an image. However, the introduction of a higher-order statistic tensor will benefit a lot in the anomaly detection for hyperspectral images.
Although the introduction of coskewness tensor benefits anomaly detection a lot, COSD may suffer from larger computational complexity. Figure 7 shows the computational complexity (measured by the required float operations, flops) for RXD and COSD. Assume the size of the hyperspectral data is N pixels and L bands. The flops required for RXD is  while that for COSD is
while that for COSD is  . We can see that from Fig. 7, COSD is more sensitive to the number of bands. When L is relatively large (for instance, >50), the computational complexity of COSD is about
. We can see that from Fig. 7, COSD is more sensitive to the number of bands. When L is relatively large (for instance, >50), the computational complexity of COSD is about  times of that of RXD.
times of that of RXD.
It is noticeable that since the COSD method can be considered as the extension of the RXD method in formula expression from the 2nd-order statistics (covariance matrix) to the 3rd-order statistics (coskewness tensor), all the other 2nd-order statistics based anomaly detection methods (such as modified RX, weighted RX, causal RX, DWEST, NSWTD) can be simply extended to those 3rd-order statistics based ones or even higher-order statistics based ones. The advantage of our COSD algorithm in detecting anomaly of hyperspectral image ensures a rationality of this extension.
In conclusion, the anomalies generally show strong features in the high-order statistics. Thus, this paper presents a new anomaly detection method COSD based on third-order statistical tensor. Formally, the COSD is the natural extension of RXD from second-order to third-order statistics. Essentially, the COSD take full advantage of angle information, which ensures the validity of COSD.
Methods
RXD
The RXD is a detector proposed by Reed and Yu4. For each pixel vector r in an image, RXD can be implemented by a operator specified by

where  is the mean vector of the image, K is the sample covariance matrix of the image and N is the number of pixels. δRXD(r) in Eq.(1) has the same form as Mahalanobis distance. The covariance matrix K can be decomposed as: K = EDET, where D = diag{λ1, λ2,…, λL}; E is the eigenvectors matrix of K. We denotes
is the mean vector of the image, K is the sample covariance matrix of the image and N is the number of pixels. δRXD(r) in Eq.(1) has the same form as Mahalanobis distance. The covariance matrix K can be decomposed as: K = EDET, where D = diag{λ1, λ2,…, λL}; E is the eigenvectors matrix of K. We denotes  as a whitening operator of the image. Then eq.(1) can be transformed as
as a whitening operator of the image. Then eq.(1) can be transformed as

From Eq. (2) we can see that, δRXD(r) is actually the Euclidean distance of r and μ of the whitened image.
Tensor introduction
A real m-order n-dimensional tensor  consists of nm real entries19, represented as
consists of nm real entries19, represented as  where ij = 1,…,n for j = 1,…, m. Fig. 8 shows an example of third-order 4-dimensional tensor. The tensor
where ij = 1,…,n for j = 1,…, m. Fig. 8 shows an example of third-order 4-dimensional tensor. The tensor  is supersymmetric if its entries are invariant under any permutation of their indices20, or mathematically, aijk = aikj = ajik = ajki = akij = akji.
is supersymmetric if its entries are invariant under any permutation of their indices20, or mathematically, aijk = aikj = ajik = ajki = akij = akji.
The tensor  defines an mth-degree homogeneous polynomial
defines an mth-degree homogeneous polynomial

where x = [x1, …, xn]T, xm is a tensor with m orders, n dimension and rank being 120 and its elements are respectively  where ij = 1, …, n for j = 1,…, m.
where ij = 1, …, n for j = 1,…, m.  is the tensor product of
is the tensor product of  and xm19. For example, when m = 2,
and xm19. For example, when m = 2,  is a matrix of n*n and
is a matrix of n*n and  . For m-order tensors,
. For m-order tensors,  can be decomposed in m steps as following:
can be decomposed in m steps as following:

where ×i denotes the i-mode product operator. Fig. 9 shows the explanation of the multiplication of a third-way tensor and a vector which yields a scalar. As will be seen later, that scalar is the corresponding skewness in the direction x if  is the coskewness tensor.
is the coskewness tensor.
For a hyperspectral image data set S = {r1,…, rN}, its m-order cumulant matrix (tensor) is defined as:

where ri is the spectral column vector of an image;  is a m-order L-dimensional tensor (where L is the number of bands in the image) with rank being 1. Obviously, the m-order statistical tensor
is a m-order L-dimensional tensor (where L is the number of bands in the image) with rank being 1. Obviously, the m-order statistical tensor  is a supersymmetric tensor. This paper will focus on the research of anomaly extraction for the hyperspectral image by using the high-order statistical tensor.
is a supersymmetric tensor. This paper will focus on the research of anomaly extraction for the hyperspectral image by using the high-order statistical tensor.
coskewness tensor detector (COSD)
For a hyperspectral image data set  , suppose that
, suppose that  and
and  , where I is L*L unit matrix. It means that each band of the image has a variance of 1 and the correlation coefficient between the bands is zero. That is to say, the hyperspectral data has been normalized. It is not difficult to reach these two conditions. If the mean vector of the image is not zero, it can be achieved by moving the origin of the image to the mean vector. Besides, the real hyperspectral image can meet the second condition by data whitening.
, where I is L*L unit matrix. It means that each band of the image has a variance of 1 and the correlation coefficient between the bands is zero. That is to say, the hyperspectral data has been normalized. It is not difficult to reach these two conditions. If the mean vector of the image is not zero, it can be achieved by moving the origin of the image to the mean vector. Besides, the real hyperspectral image can meet the second condition by data whitening.
Here, we propose a new anomaly detector, named high-order statistic detector (HOSD), which is defined as follows:

where  is a high-order statistic tensor of the image defined as Eq.(5); r is the pixel vector of the image. Similar to Eq.(3),
is a high-order statistic tensor of the image defined as Eq.(5); r is the pixel vector of the image. Similar to Eq.(3),  is a scalar which is the tensor product of the m-order statistic tensor
is a scalar which is the tensor product of the m-order statistic tensor  and
and  . In this paper, we will discuss a case where m = 3. And then Eq.(5) can be transformed as
. In this paper, we will discuss a case where m = 3. And then Eq.(5) can be transformed as

which can be called as coskewness tensor detector (COSD) and here  is the coskewness tensor. Apparently the coskewness tensor is a supersymmetric third-order tensor with the dimension of L × L × L.
is the coskewness tensor. Apparently the coskewness tensor is a supersymmetric third-order tensor with the dimension of L × L × L.
Like RXD, the coskewness tensor based anomaly detector also uses all pixels of the image by eq. (7) to get a gray image, where the anomalies of the image will appear to be very bright or dark. The dark pixels in the gray image are caused by the negative values from Eq. (7). Therefore, we usually determine anomaly pixel by using the absolute value of the gray image.
In Eq. (7), if  is a unit vector, then
is a unit vector, then  is the skewness of the image against the direction of
is the skewness of the image against the direction of  . Eq.(7) can be transformed as follows
. Eq.(7) can be transformed as follows

From Eq. (8), we can see that the anomaly extraction using Eq. (7) is mainly dependent on two indices: One is the skewness and the other is the cube of the 2-norms. If we eliminate the item  from Eq.(8), the COSD operator becomes a normalized COSD (NCOSD) operator
from Eq.(8), the COSD operator becomes a normalized COSD (NCOSD) operator

Practically,  is the skewness of image data against the direction of
is the skewness of image data against the direction of  .
.
Let us assume that hyperspectral image is composed of background and abnormal pixels,

where  is the whitened hyperspectral image;
is the whitened hyperspectral image;  is background (Nb is the number of background pixels); and
is background (Nb is the number of background pixels); and  is anomaly (Na is the number of abnormal pixels). It is obvious that N = Nb + Na. The coskewness tensor of the image can be transformed as
is anomaly (Na is the number of abnormal pixels). It is obvious that N = Nb + Na. The coskewness tensor of the image can be transformed as

where  is composed of background pixels and
is composed of background pixels and  is composed of abnormal pixels. In this study, we just discuss the case that only one class of anomaly lies in the image and denote the spectrum of anomaly as
is composed of abnormal pixels. In this study, we just discuss the case that only one class of anomaly lies in the image and denote the spectrum of anomaly as  , Then we have
, Then we have

and the coskewness tensor of the image can be transformed as:

In general, the number of abnormal pixels in an image is very small, thus μb ≈ μ = 0, where  is the mean vector of the background image. Accordingly,
is the mean vector of the background image. Accordingly,  can be approximately considered as the coskewness tensor of the background image. If we assume that the background image fits a Gaussian distribution, we can get
can be approximately considered as the coskewness tensor of the background image. If we assume that the background image fits a Gaussian distribution, we can get

It means that all the elements of  are close to zero. Thus the skewness of the image in the direction of
are close to zero. Thus the skewness of the image in the direction of  can be expressed as
can be expressed as

where θ is the angle between the vector  and
and  . Considering eq.(15), eq.(8) can be rewritten as
. Considering eq.(15), eq.(8) can be rewritten as

Since  is an image after centering and whitening, the RX operator can be expressed as
is an image after centering and whitening, the RX operator can be expressed as

From eq.(15–17), it can be seen that there are distinguished differences among RX, NCOSD and COSD. Specifically, RXD depends only on the distance between a pixel and the origin in the feature space of the whitened image. Only when abnormal pixels are far away from the origin and all the background pixels are relatively close to the origin, RXD can achieve a good anomaly detection result. NCOSD is based on the skewness of the image and its detection performance is dependent on angles between an abnormal pixel and all the background pixels. When all the angles are large, NCOSD can get a good detection result. As for COSD, it does not only take the distance into account, but also the angle. So it can overcome shortcomings of both RXD and NCOSD, both of which focus only on one single index.
References
Tan, K., Li, E., Du, Q. & Du, P. Hyperspectral Image Classification Using Band Selection and Morphological Profiles. IEEE J. Sel. Topics Appl. Earth Observ. 7, 40–48 (2014).
Chang, C.-I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification (Plenum Press, New York, 2003).
Manolakis, D. & Shaw, G. Detection algorithoms for hyperspectral imaging applications. IEEE Signal Process Mag 19, 29–43 (2002).
Reed, I. S. & Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust Speech Signal Process 38, 1760–1770 (1990).
Yu, X., Reed, I. S. & Stocker, A. D. Comparative performance analysis of adaptive multispectral detectors. IEEE Trans. Signal Process 41, 2639–2656 (1993).
Yu, X., Hoff, L. E., Reed, I. S., Chen, A. M. & Stotts, L. B. Automatic target detection and recognition in multiband imagery: A unified ML detection and estimation approach. IEEE Trans. Image Process 6, 143–156 (1997).
Chang, C. I. & Chiang, S. S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens 40, 1314–1325 (2002).
Hsueh, M. & Chang, C. I. Adaptive causal anomaly detection for hyperspectral imagery. In: IEEE International Geoscience & Remote Sensing Symposium 5, 3222–3224 (2004).
Harsanyi, J. C. Detection and classification of subpixel spectral signatures in hyperspectral image sequences Ph.D thesis, Baltimore, (1993).
Kwon, H. Adaptive anomaly detection using subspace separation for hyperspectral imagery. Opt Eng 42, 3342–3351 (2003).
Liu, W. & Chang, C. I. A nested spatial window-based approach to target detection for hyperspectral imagery. In: IEEE International Geoscience and Remote Sensing Symposium 20–24 (Alaska, 2004).
Rosario, D. A nonparametric F-distribution anomaly detector for hyperspectral imagery. In: Aerospace Conference, IEEE 2022–2029 (2005).
Schwerizer, S. M. & Moura, J. M. F. Efficient detection in hyperspectral imagery. IEEE Trans. Image Process 10, 584–597 (2001).
Gu, Y., Liu, Y. & Zhang, Y. A selective KPCA algorithm based on high-order statistics for anomaly detection in hyperspectral imagery. IEEE Geosci. Remote Sens Lett 5, 43–47 (2008).
Chiang, S.-S., Chang, C.-I. & Ginsberg, I. W. Unsupervised target detection in hyperspectral images using projection pursuit. IEEE Trans. Geosci. Remote Sens 39, 1380–1391 (2001).
Xun, L. & Fang, Y. Anomaly Detection Based on High-order Statistics in Hyperspectral Imagery. In: The Sixth World Congress on Intelligent Control and Automation 2, 10416–10419 (2006).
Ren, H. & Chang, Y.-L. A Parallel Approach for Initialization of High-Order Statistics Anomaly Detection in hyperspectral imagery. In: IEEE International Geoscience & Remote Sensing Symposium 2, II-1017-II-1020 (2008).
Geng, X., Ji, L., Zhao, Y. & Wang, F. A small target detection method for the hyperpectral image based on high-oder singular value decomposition (HOSVD). IEEE Geosci. Remote Sens Lett 10, 1305–1308 (2013).
Qi, L. Eigenvalues of a real supersymmetric tensor. J. Symbolic Comput. 40, 1302–1324 (2005).
Kofidis, E. & Regalia, P. On the best rank-1 approximation of higher-order supersymmetric tensors. SIAM J Matrix Anal A 23, 863–884 (2002).
Acknowledgements
We are very grateful to Dr. Suhong Liu from Beijing Normal University, China for her great help in language.
Author information
Authors and Affiliations
Contributions
X.G. conceived the idea. X.G., K.S., L.J. and Y.Z. designed and performed the experiments and analyzed the data. X.G., K.S. and L.J. wrote the main manuscript text. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Geng, X., Sun, K., Ji, L. et al. A High-Order Statistical Tensor Based Algorithm for Anomaly Detection in Hyperspectral Imagery. Sci Rep 4, 6869 (2014). https://doi.org/10.1038/srep06869
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06869
This article is cited by
-
Fast quantifying collision strength index of ethylene-vinyl acetate copolymer coverings on the fields based on near infrared hyperspectral imaging techniques
Scientific Reports (2016)
-
What’s Wrong with the Murals at the Mogao Grottoes: A Near-Infrared Hyperspectral Imaging Method
Scientific Reports (2015)
-
Joint Skewness and Its Application in Unsupervised Band Selection for Small Target Detection
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.