Abstract
Humans are fundamentally social. They form societies which consist of hierarchically layered nested groups of various quality, size and structure. The anthropologic literature has classified these groups as support cliques, sympathy groups, bands, cognitive groups, tribes, linguistic groups and so on. Anthropologic data show that, on average, each group consists of approximately three subgroups. However, a general understanding of the structural dependence of groups at different layers is largely missing. We extend these early findings to a very large high-precision large-scale internet-based social network data. We analyse the organisational structure of a complete, multi-relational, large social multiplex network of a human society consisting of about 400,000 odd players of an open-ended massive multiplayer online game for which we know all about their various group memberships at different layers. Remarkably, the online players' society exhibits the same type of structured hierarchical layers as found in hunter-gatherer societies. Our findings suggest that the hierarchical organisation of human society is deeply nested in human psychology.
Similar content being viewed by others
Introduction
Humans naturally organise in groups and societies. They have progressively dominated their environment by the strength and creativity that emerges as a consequence of organising within groups. It is well recognised that human groups are highly structured and the anthropological literature has loosely classified them according to their size and function, such as families, support cliques, sympathy groups, bands, cognitive groups, tribes, chiefdoms, linguistic groups and so on1,2,3,4,5,6,7,8. Recently, combining data on human grouping patterns in a comprehensive and systematic study, Zhou et al.9 identified a quantitative discrete hierarchy of group sizes with a preferred scaling ratio close to 3, which was later confirmed for hunter-gatherer groups10 and for other mammalian societies11. A hierarchy of nested groups was also found in an email communication network, the collaboration network of Jazz musicians and networks of scientific collaborations, with the bifurcation ratio between the number of branches with two successive values of the Strahler index between 3.0 and 5.712. Note that this bifurcation ratio quantifies a metric property of the branching network and is not the same as the scaling ratio between group sizes discussed here. In the literature the term ‘nesting’ is used with two different meanings. In ecology, this term is used for bipartite networks, like plant-animal pollination networks. In the idealised case, this situation resembles a Russian matryoshka doll: each group, i.e. the plants pollinated by a given pollinator species, has exactly one subgroup in the next lower layer, which are the plants pollinated by the next more specialist pollinator species and one super-group in the next higher layer, which are the plants pollinated by the next more generalist pollinator species. Various metrics exist to measure the agreement of a given bipartite network with the idealised case13. Nesting according to this notion has been observed in ecologic and economic networks14,15. In10 and in this paper, the term ‘nesting’ is used in a broader sense: groups may contain more than one subgroup and are not derived from a bipartite network. In the following we will use the term ‘hierarchy’ similar to16, referring to a system of nested groups, (i.e. groups containing subgroups, which in turn contain sub-subgroups and so on), not to a system of control or power. However, assuming that each group has a leader, the hierarchy (nesting relation) of groups directly corresponds to a hierarchy (power relation) of group leaders.
We analyse comprehensive data from a society, consisting of the players of the massive multiplayer online game (MMOG) Pardus (http://www.pardus.at). Such online platforms provide a new way of observing hundreds of thousands of interacting individuals who are engaged in social and economic activities, enabling quantitative socioeconomic research17,18,19,20,21,22,23,24,25. Complementing traditional methods of social science such as small-scale questionnaire-based approaches, MMOGs allow the study of complete societies, which are free of any interviewer bias or laboratory effects, since users are typically not aware that their actions are logged during playing.
Extensive previous studies on Pardus have shown remarkable similarities between this virtual world and real-world societies, in terms of network structure19,20,21, social behaviour22,23 and even mobility patterns24 and wealth inequalities25. Players in Pardus control characters (avatars) who ‘live’ in a virtual, futuristic universe. Every character is the pilot of a spacecraft, which he can use to roam the universe and transport goods for trade. Players can interact with others in many ways, cooperative or destructive. There is no explicit ‘winning’ in Pardus, but rather players are free to set their own goals.
Since the game went online in 2004, more than 400,000 people have played it. Pardus provides an internal one-to-one messaging system comparable to emails and players can express their sympathy toward other players by marking them as friend. There are no restrictions on these interactions and they are completely private, i.e. only those players that are involved in the interaction, know about it.
As a human society, even though being pure virtual, Pardus is a highly structured social system, that operates simultaneously on different levels and social scales. Players interact with each other in a multitude of ways, creating a superposition of dense social networks of different types, that are referred to as multiplex networks21. These social networks include friendship-, trade- and communication networks. On a low level, within the friendship and communication networks, small friendship- and support groups appear. On a slightly higher level people organise in bigger groups, or clubs. Players can explicitly create formal social groups and register these as alliances. The game provides a series of tools to facilitate administration of the groups. These groups can be thought of as clubs, or societies, that often form to express the common interests of its members. The size of the alliances is not restricted in any way. For the analysis, however, we excluded alliances with less than three members, assuming that they are in the process of being disbanded or created, or that they at least do not act as a social group in the usual way. Interestingly, even though there is no upper limit for the sizes of alliances, we find that the largest alliance has 136 members. This is remarkably close to the so-called Dunbar number8. Dunbar conjectured that humans could not form tight groups with more than about 150 members due to their limited cognitive capacity that is needed to maintain social links. It has been argued to be the maximal number of people with whom a personal relation can be maintained on one of the various layers of human society26. This number is not assumed to change by the use of digital communication media26. In fact Dunbar's number has been reported as an upper limit to the number for the friendship- and communication networks in Pardus19. A possible mechanism altering the structure of society and generating larger groups is communication with many people at once26. At the next level of organisation, the largest organized groups in the game are three ‘political’ factions, which are pre-defined by the game designers of Pardus. Factions contain about 2,000 members each. Although the number of factions in the game is limited to three, their relative sizes and numbers of memberships are variable, since players can freely decide whether to be member of a given faction or not. Also each alliance may decide to belong to one of the three factions. The average size of the total Pardus society is about 7,000 active players at any given time. Table I contains all group sizes at the various levels and the observed number of the groups within the game. Averages over five observations on different days are shown. In the following section we will assign level indices to these different ways of organisation into groups.
Ego-network of one particular player on day 1200 showing hierarchical organisation.
Blue ellipses depict the various layers of organisation. Dots represent players; dashed lines connect identical players across layers; crosses denote players that are not present in the next layer. Thick dark red lines represent strongest ties, forming  , green lines represent friendship links, forming
, green lines represent friendship links, forming  and dotted pink lines mark membership in a common alliance. The layers contain 1, 4, 12 and 24 individuals, respectively. Layer 3 (friends) is typically not a subset of layer 4 (alliance). For clarity, only links to the ego are drawn.
and dotted pink lines mark membership in a common alliance. The layers contain 1, 4, 12 and 24 individuals, respectively. Layer 3 (friends) is typically not a subset of layer 4 (alliance). For clarity, only links to the ego are drawn.
The possibility for diverse levels of organisation gives rise to a complex hierarchical structure of society, which in the following we quantify in two complementary ways, first using the Horton-Strahler measure of branching complexity and second by studying the structure of the distribution of group sizes directly.
Results
We use Horton-Strahler scaling to quantify the scaling of the nested social groups in Pardus. The Horton order, (also called Strahler number) as used originally, denotes the rank of streams and rivers, where smaller rivers with lower Horton order combine into larger rivers with higher Horton order. Here, we apply this idea to social groups: some groups of lower order together form a group of higher order. Figure 1 shows the social network of one particular player and the nested groups around him. The innermost layer, Horton order h = 1, is the trivial group consisting of one person, the ‘ego’. Layer 2 (h = 2) contains closest friends of the ego, defined by both a friendship marking and at least one communication event within the last 30 days. Layer 3 (h = 3) includes more casual relations, in particular all players that ego has marked as a friend, or by whom ego was marked as friend. Layer 4 (h = 4) contains the fellow alliance members of the ego. Layer 5 (h = 5), corresponding to the communication clusters, is obtained by applying a community detection algorithm (Louvain algorithm)27,28 to the communication network of the players (see Methods). We tested explicitly that layer 5 is an organisational layer in its own right, whose communities are predominantly subsets of the factions (h = 6) and supersets of the alliances (h = 4, see Methods). The communication clusters correspond to groups of cooperating alliances, but are not officially declared nor directly visible for the players. Layer 6 (h = 6) contains the three factions. Being members of the same faction can be compared to being compatriots in the real world, meaning this is a rather weak link. Finally, layer 7 (h = 7) is the entire society.
In the real world, it is known that the lower layers correspond to higher emotional closeness and more time invested in the respective relationships6,9,26. In the case of Pardus we know, by construction, that more time is invested in relationships on layer 2 than on layer 3. It seems plausible that the time spent on links in the higher layers is lower. However, we have no explicit knowledge of the time spent to establish and maintain these links. To keep the privacy of players, we do not have information on the content of messages between players and we are not able to measure emotional closeness. We assume that emotional closeness is generally low in the entire game since communication in the game is text-based, which has been identified as hardly satisfying emotionally26.
Following Hill et al.11, we calculate the average group size at Horton order h, G(h) (See Methods). We observe that group size follows an exponential increase as a function of the Horton order, see Fig. 2 a, which shows that G(h) ~ ph, with a scaling ratio of p = 4.4.
Analysis of group size scaling: (a) Horton plot: average size of groups per order. ln(p) is determined by a simple least squares fit of ln (G(h)) = C + h ln(p) to the data as p = 4.42 ± 0.08. (b) Estimated probability density of group sizes in Pardus, obtained as Gaussian kernel estimation with bandwidth σ = 0.14 acting on ln(s) (see Methods). (c) Generalized (H, q)-derivative of f(s) for H = 0.5 and q = 0.8 (see Methods). (d) Lomb periodogram of the (H, q)-derivative of f(s) for different values of H and q (see Methods). Peaks at ω = 4.3 ± 0.1 (7.7 ± 0.1) (marked with black vertical lines) correspond to scaling ratios p = exp(2π/ω) = 4.3 ± 0.2 (2.26 ± 0.03).
A second, independent way to affirm discrete scale invariant structure is obtained by directly analysing the distribution of group sizes, following the approach presented by Zhou et al.9. See Methods for details on the following concepts and variables. To this end we use a Gaussian kernel estimator of the probability density f(s) (shown in Fig. 2 b) of player group sizes in our data, obtaining a smoothed version of the histogram. We calculate the generalised (H, q)-derivative29,30 of f(s), which generalises the q-derivative31,32, for multiple values of H and q, see Fig. 2 c. The parameter H stands for the Hurst exponent used to rescale the derivative, while q controls the scale factor of the q-derivative. Coupled with the Lomb-periodogram33, which shows the contribution of given frequencies to a signal, the (H, q)-derivative has been shown to be very efficient for identifying log-periodicity in signals29,30. Log-periodicity is the observable signature of discrete scale invariance34. Our data do not allow us to precisely determine the value of H and q. Rather, we test for robustness of the presence of discrete scale invariance by sampling the parameter space by using values of H between 0.5 and 0.9 with a spacing of 0.08 and values of q between 0.65 and 0.95 with a spacing of 0.06 in Fig. 2 d. For all these values, the Lomb periodogram of the (H, q)-derivative of f(s) gives a highly significant peak35 at the angular log-frequencies ω = 4.3, corresponding to a scaling ratio p = exp(2π/ω) = 4.3. Further, one can clearly see the second and third harmonics, which gives additional support for the existence of log-periodicity36 and therefore hierarchical and discrete scale invariance.
Discussion
We have analysed comprehensive data of social organisation at different layers from the human society of a virtual world. In particular we quantified how and to what extent this society is organised in layers of hierarchically nested groups. Using two independent methods, the Horton-Strahler scaling and a second approach based on the generalised (H, q)-derivative of the size distribution, we found that the group sizes show discrete scale invariance with a preferred scaling ratio of 4.3–4.4.
The immediate question arises if the observed organisational structure is the result of humans self-organising into fractal structures or if these findings are consequences of the structure of the Pardus game environment. Communication and establishing and terminating friendship relations are not restricted in any way in the game, so that layers 2 and 3 emerge as a direct consequence of social interactions, unhindered by the game structure. We defined these layers in an attempt to capture the equivalent of ‘support cliques’ and ‘sympathy groups6’ in the virtual world. The alliances which form layer 4, are naturally formed social groups that are administered by tools provided by the game, but the game itself does in no way suggest alliance memberships to players. Memberships are established as a consequence of a decision of a player. The decision can be strongly influenced by the opinions of the players' friends and other sources of information, but not as a consequence of any ‘game mechanics’. In particular, the size of the alliances is not restricted in any way. For the analysis, however, we only counted alliances with at least three members. The communication clusters that constitute layer 5 are identified in the communication networks by standard community detection methods (see Methods). Since these are structural elements that are objectively found within a self-organised social network, again there is no direct influence by the game rules on the formation or definition of this layer. The factions, layer 6, are determined by the game mechanics in the sense that there are only three factions at any time. Other than this limitation, players decide if they want to be a member in one of factions or remain without such a membership. As a consequence of the limitation to three factions the scaling ratio between layers 6 and 7 (total population) can not be below 3. Excluding the factions from the analysis does not change the results much: Acknowledging that an additional layer with unknown group sizes exists above the communication clusters, the Horton-Strahler scaling gives p = 4.3. In the Lomb periodogram, omitting the factions shifts the first peak to ω = 3.9 and p = 5.0, while the second peak hardly changes to ω = 7.8 and p = 2.2.
Hierarchical organisation showing discrete scale invariance has been observed in real-world societies before. Measured scaling ratios have been reported to be 3.2 in9 and 3.77 in10. It has been suggested in26 that the different results in9 and10 originate from different methodology, but since we find nearly the same scaling ratios using both methodologies, this seems unlikely. In14,15, a different notion of nesting is assumed. Therefore, group sizes are not studied and no scaling ratio is measured. The scaling ratio of 4.3–4.4 presented here for the Pardus data clearly is above these values, however it falls nicely within the range of the bifurcation ratio found in12. There the scaling ratio between the number of branches with two successive values of the Strahler index has been computed, which can not be mapped exactly onto the scaling ratio between group sizes. The highest bifurcation ratio, 5.7, was found for an email communication network. This might suggest that digital communication media slightly change the structure of human society as speculated in26, in particular fostering larger groups containing more subgroups. In summary we present clear further evidence for the fractal nature of hierarchical organisation of human society. Remarkably this organisational principle that has been found to apply in so many different settings and contexts, is also found in societies that are completely detached from constraints of the real, physical world. The existence of this social organisational principle in virtual societies is an indication of how deeply it is rooted in human psychology.
Methods
Data
Pardus is partitioned into three independent games, called ‘universes’. Here, we focus on one of them, the ‘Artemis’ universe. In the game, we have complete information on a multitude of temporal social networks, including the friendship-, communication- and trading networks21. Data are available over 1238 days. We take snapshots of the friendship- and communication network and of group affiliations on days 240, 480, 720, 960 and 1200 since the opening of the ‘Artemis’ universe on June 12, 2007. In more formal terms, we have a multiplex  , where α indicates the type of the link, here friendship and communication.
, where α indicates the type of the link, here friendship and communication.  if i has marked j as friend before t (and has not revoked this marking since) and zero otherwise.
if i has marked j as friend before t (and has not revoked this marking since) and zero otherwise.  if i has sent a message to j in the time [t − 30d, t] and zero otherwise. Further, we consider the symmetrisation of the multiplex:
if i has sent a message to j in the time [t − 30d, t] and zero otherwise. Further, we consider the symmetrisation of the multiplex:  if
if  or
or  . Groups are defined at seven layers, starting with the ego (h = 1), where
. Groups are defined at seven layers, starting with the ego (h = 1), where  is the group of layer h to which i belongs. Support cliques (h = 2) are defined as the set of an individual's friends with whom he has communicated at least once within the last month:
is the group of layer h to which i belongs. Support cliques (h = 2) are defined as the set of an individual's friends with whom he has communicated at least once within the last month:  . Sympathy groups (h = 3) are defined as the set of an individual's friends:
. Sympathy groups (h = 3) are defined as the set of an individual's friends:  . Layer 4 consists of the so-called ‘alliances’ (h = 4), which are clubs that can be created in the game and where all memberships are known. The same is true for the ‘factions’ (h = 6). An additional layer of grouping (h = 5) is found by applying the Louvain algorithm27,28 to
. Layer 4 consists of the so-called ‘alliances’ (h = 4), which are clubs that can be created in the game and where all memberships are known. The same is true for the ‘factions’ (h = 6). An additional layer of grouping (h = 5) is found by applying the Louvain algorithm27,28 to  . Note that the Louvain algorithm confirms the other lower layers h = 1 to h = 4. The last layer is the whole society (h = 7). We consider only alliances and communication clusters with at least three members.
. Note that the Louvain algorithm confirms the other lower layers h = 1 to h = 4. The last layer is the whole society (h = 7). We consider only alliances and communication clusters with at least three members.  might be empty for h > 1. For the layers 2 and 3, we define the average group size G(h, t) by taking the mean group size of all players having a (non-empty) support clique or sympathy group, respectively:
might be empty for h > 1. For the layers 2 and 3, we define the average group size G(h, t) by taking the mean group size of all players having a (non-empty) support clique or sympathy group, respectively:  . For layers 4 to 6, the average runs over all distinct groups in this layer.
. For layers 4 to 6, the average runs over all distinct groups in this layer.
Layer 5: communication clusters
Layer 5 is obtained by applying the Louvain algorithm27,28 to the communication network of the players. The Louvain algorithm finds communities, i.e. densely linked parts of the network, by heuristically maximising modularity. In an iterative way, nodes are grouped in communities, which are treated as nodes of a ‘coarse-grained’ network in the next iteration, thereby finding multiple layers of communities. We find that the lower layers found by the Louvain algorithm roughly agree with the layers defined above. The communities in the highest layer found by the Louvain algorithm are the communication clusters and contain 294 players each (ignoring communities with less than three members). Results for every day in our data set are obtained from averages over five runs of the algorithm. When comparing the communication clusters to the factions, we find that about 76% of the members of a communication cluster are in the same faction. Comparing communication clusters to the alliances we find that about 84% of the members of an alliance are in the same communication cluster on average. To further quantify the similarity between communities found by the Louvain algorithm and the factions and alliances, we calculate the Fowlkes-Mallows index37,38 (see below). We compare layer 5 with the factions (layer 6) and the alliances (layer 4). As a null model we generate random communities of the same sizes as those found by the Louvain algorithm: each community labelling (as found in any of the five runs of the Louvain algorithm) is reshuffled ten times and the respective Fowlkes-Mallows indices for layer 5 – factions and layer 5 – alliances are computed.
(see below). We compare layer 5 with the factions (layer 6) and the alliances (layer 4). As a null model we generate random communities of the same sizes as those found by the Louvain algorithm: each community labelling (as found in any of the five runs of the Louvain algorithm) is reshuffled ten times and the respective Fowlkes-Mallows indices for layer 5 – factions and layer 5 – alliances are computed.  is defined as the average over the five iterations of the Louvain algorithm, the ten shuffled versions and the five days of observation. For layer 5 – factions, we find
is defined as the average over the five iterations of the Louvain algorithm, the ten shuffled versions and the five days of observation. For layer 5 – factions, we find  , with
, with  , which suggests that the detected communities are predominantly subsets of the factions. For the layer 5 – alliances case we get
, which suggests that the detected communities are predominantly subsets of the factions. For the layer 5 – alliances case we get  and
and  , implying that the layer 5 communities are also mainly supersets of the alliances. These results indicate that layer 5 is indeed an organisational layer in its own right, located between the factions (layer 6) and the alliances (layer 4).
, implying that the layer 5 communities are also mainly supersets of the alliances. These results indicate that layer 5 is indeed an organisational layer in its own right, located between the factions (layer 6) and the alliances (layer 4).
Fowlkes-Mallows index 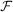
 is a metric to evaluate the similarity of two clusterings (i.e. results of community labelling). For identical clusterings,
is a metric to evaluate the similarity of two clusterings (i.e. results of community labelling). For identical clusterings,  , while for totally unrelated clusterings,
, while for totally unrelated clusterings,  , given the number of clusters is large.
, given the number of clusters is large.  is defined as37,38:
is defined as37,38:

where TP (“true positives”) is the number of pairs of elements that are in a common community in both compared clusterings, FP (“false positives”) is the number of pairs that are in a common community in clustering 1, but belong to two different communities in clustering 2. FN (“false negatives”) is the number of pairs that are found in a common community in clustering 2, but belong to two different communities in clustering 1.
Gaussian kernel estimator
The Gaussian kernel estimator is a tool to estimate the probability density f(s) to observe one particular group size s from N data points si. In other words, it could be described as a smoothed histogram. The Gaussian kernel estimator in the way we use it is defined as  , where
, where  is a zero-mean Gaussian distribution with standard deviation σ = 0.14. Varying σ by a factor of two in either direction does not shift the position of the peaks in the Lomb periodogram significantly, but for the case of 2σ, the high frequencies are filtered out.
is a zero-mean Gaussian distribution with standard deviation σ = 0.14. Varying σ by a factor of two in either direction does not shift the position of the peaks in the Lomb periodogram significantly, but for the case of 2σ, the high frequencies are filtered out.
Generalized (H, q)-derivative
The (H, q)-derivative is a generalisation of the q-derivative Dqf(s), defined in31,32 as  , into29,30
, into29,30

The q-derivative Dqf(s) recovers the standard definition of a derivative in the limit q → 1 with the difference that the increment δs of the argument s of the function is proportional to s according to δs = (1 − q)s. The q-derivative Dqf(s) is thus a natural metric to detect scaling properties in the function f(s). Scanning q provides information on the possible existence of preferred scaling ratios associated with some discrete scale invariance of the function. The (H, q)-derivative  provides a very powerful generalisation of the q-derivative Dqf(s) for functions that are not smooth but rather characterised by a large stochasticity with local scaling characterised by a local Hurst exponent H ≠ 1 (the ballistic or smooth case). The choice H = 1/2 allows one to analyse stochastic functions that scale like a random walk, while H > 1/2 (resp. H < 1/2) is suitable for persistent (resp. anti-persistent) random walks. Previous synthetic tests and real-life applications have shown that the (H, q)-derivative
provides a very powerful generalisation of the q-derivative Dqf(s) for functions that are not smooth but rather characterised by a large stochasticity with local scaling characterised by a local Hurst exponent H ≠ 1 (the ballistic or smooth case). The choice H = 1/2 allows one to analyse stochastic functions that scale like a random walk, while H > 1/2 (resp. H < 1/2) is suitable for persistent (resp. anti-persistent) random walks. Previous synthetic tests and real-life applications have shown that the (H, q)-derivative  allows for an adaptive de-trending and enhances possible discrete scale structures while testing for robustness29,30.
allows for an adaptive de-trending and enhances possible discrete scale structures while testing for robustness29,30.
Lomb periodogram
The Lomb periodogram is a method for spectral analysis, i.e. for quantifying the contribution of each frequency to a given signal, based on the least squares fit of sine functions to the data33. Compared to the better known Fourier transform, it has the advantage that it can be applied to unevenly sampled data, as occurs when using the logarithm of sizes. See Fig. 3 that illustrates the whole process of recovering the preferred scaling ratio using the Lomb periodogram applied to the (H, q)-derivative of the kernel estimation of the density distribution of a noisy log-periodic signal.
Detection of log-periodicity (illustration): (a) Data points with factor three between each other (blue), log-periodic function cos(ω0 ln(s)) with ω0 = 2π/ln(3) ≈ 5.72 (black). (b) Same as a, but with logarithmic x-axis to visualise the log-periodicity. (c) ln(s) is perturbed, i.e. drawn from a (sum of) normal distribution(s) with mean ln(3) and variance 0.1 (blue). Black: Analytical probability density for the data. (d) Probability density as inferred from the data by Gaussian kernel estimation of ln(s) with bandwidth 0.1. (e) Generalized (H, q)-derivative of f(s), with q = 0.8 and H = 0.5. (f) Lomb periodogram of  as a function of ln(f(s)). The main peak is close to the expected value ω0 (marked in black). Additionally, a peak close to the second harmonic 2ω0 is visible.
as a function of ln(f(s)). The main peak is close to the expected value ω0 (marked in black). Additionally, a peak close to the second harmonic 2ω0 is visible.
References
Kottak, C. P. Mirror for Humanity: A Concise Introduction to Cultural Anthropology (McGraw-Hill, Boston, 2007), 6th edn.
Binford, L. R. Constructing frames of reference: an analytical method for archaeological theory building using ethnographic and environmental data sets (University of California Press, Berkeley, 2001).
Steward, J. H. Theory of Culture Change: The Methodology of Multilinear Evolution (University of Illinois Press, Champaign, 1972).
Lee, R. B. The !Kung San: men, women and work in a foraging society (Cambridge University Press, Cambridge, 1979).
Knauft, B. M. Reconsidering violence in simple human societies: homicide among the Gebusi of New Guinea. Curr. Anthropol. 28, 457–500 (1987).
Dunbar, R. I. M. & Spoors, M. Social networks, support cliques and kinship. Hum. Nat. 6, 273–290 (1995).
Hill, R. A. & Dunbar, R. I. M. Social network size in humans. Hum. Nat. 14, 53–72 (2003).
Dunbar, R. I. M. Co-evolution of neocortex size, group size and language in humans. Behavi. and Brain Sci. 16, 681–735 (1993).
Zhou, W.-X., Sornette, D., Hill, R. A. & Dunbar, R. I. M. Discrete hierarchical organisation of social group sizes. Proc. R. Soc. B 272, 439–444 (2005).
Hamilton, M. J., Milne, B. T., Walker, R. S., Burger, O. & Brown, J. H. The complex structure of hunter- gatherer social networks. Proc. R. Soc. B 274, 2195–2202 (2007).
Hill, R. A., Bentley, R. A. & Dunbar, R. I. Network scaling reveals consistent fractal pattern in hierarchical mammalian societies. Biol. Lett. 4, 748–751 (2008).
Arenas, A., Danon, L., Daz-Guilera, A., Gleiser, P. & Guimer, R. Community analysis in social networks. Eur. Phys. J. B 38, 373–380 (2004).
Almeida-Neto, M., Guimarães, P., Guimarães, P. R., Loyola, R. D. & Ulrich, W. A consistent metric for nestedness analysis in ecological systems: reconciling concept and measurement. Oikos 117, 1227–1239 (2008).
Saavedra, S., Reed-Tsochas, F. & Uzzi, B. A simple model of bipartite cooperation for ecological and organizational networks. Nature 457, 463–466 (2008).
Saavedra, S., Stouffer, D. B., Uzzi, B. & Bascompte, J. Strong contributors to network persistence are the most vulnerable to extinction. Nature 478, 233–235 (2011).
Ravasz, E. & Barabási, A.-L. Hierarchical organization in complex networks. Phys. Rev. E 67, 026112 (2003).
Bainbridge, W. S. The scientific research potential of virtual worlds. Science 317, 472 (2007).
Castronova, E. Synthetic Worlds: The Business and Culture of Online Games (University of Chicago Press, Chicago, 2005).
Szell, M. & Thurner, S. Measuring social dynamics in a massive multiplayer online game. Soc. Networks 32, 313–329 (2010).
Klimek, P. & Thurner, S. Triadic closure dynamics drives scaling laws in social multiplex networks. New J. Phys. 15, 063008 (2013).
Szell, M., Lambiotte, R. & Thurner, S. Multirelational organisation of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 107, 13636–13641 (2010).
Thurner, S., Szell, M. & Sinatra, R. Emergence of good conduct, scaling and Zipf laws in human behavioral sequences in an online world. PLoS ONE 7, e29796 (2012).
Szell, M. & Thurner, S. How women organize social networks different from men. Sci. Rep. 3, 1214; 10.1038/srep01214 (2013).
Szell, M., Sinatra, R., Petri, G., Thurner, S. & Latora, V. Understanding mobility in a social petri dish. Sci. Rep. 2, 457; 10.1038/srep00457 (2012).
Fuchs, B. & Thurner, S. Behavioral and network origins of wealth inequality: Insights from a virtual world. PLoS ONE 9, e103503 (2014).
Dunbar, R. I. M. Social cognition on the internet: testing constraints on social network size. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 2192–2201 (2012).
Blondel, V., Guillaume, J.-L., Lambiotte, R. & Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, P10008 (2008).
Rubinov, M. & Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52, 1059–1069 (2010).
Zhou, W.-X. & Sornette, D. Generalized q-Analysis of Log-Periodicity: Applications to Critical Ruptures. Phys. Rev. E 6604, 046111 (2002).
Zhou, W.-X. & Sornette, D. Non-Parametric Analyses of Log-Periodic Precursors to Financial Crashes. Int. J. Mod. Phys. C 14, 1107–1126 (2003).
Erzan, A. & Eckmann, J.-P. q-analysis of fractal sets. Phys. Rev. Lett. 78, 3245–3248 (1997).
Erzan, A. Finite q-differences and the discrete renormalization group. Phys. Lett. A 225, 235–238 (1997).
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical Recipes (Cambridge University Press, New York, 2007), 3rd edn.
Sornette, D. Discrete scale invariance and complex dimensions. Phys. Rep. 297, 239–270 (1998).
Zhou, W.-X. & Sornette, D. Statistical Significance of Periodicity and Log-Periodicity with Heavy-Tailed Correlated Noise. Int. J. Mod. Phys. C 13, 137–170 (2002).
Zhou, W.-X. & Sornette, D. Evidence of Intermittent Cascades from Discrete Hierarchical Dissipation in Turbulence. Physica D 165, 94–125 (2002).
Fowlkes, E. B. & Mallows, C. L. A method for comparing two hierarchical clusterings. J. Am. Stat. Assoc. 78, 553–569 (1983).
Halkidi, M., Batistakis, Y. & Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 17, 107–145 (2001).
Acknowledgements
S.T. and B.F. acknowledge support from the Austrian Science Fund FWF P23378 and the EU FP7 Project MULTIPLEX, No. 317532.
Author information
Authors and Affiliations
Contributions
B.F., D.S. and S.T. devised the concept. B.F. analysed the data. B.F., D.S. and S.T. interpreted the results and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Fuchs, B., Sornette, D. & Thurner, S. Fractal multi-level organisation of human groups in a virtual world. Sci Rep 4, 6526 (2014). https://doi.org/10.1038/srep06526
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06526
This article is cited by
-
Evidence of the persistence and consistency of social signatures
Applied Network Science (2022)
-
Contagion of network products in small-world networks
Journal of Economic Interaction and Coordination (2019)
-
Skill complementarity enhances heterophily in collaboration networks
Scientific Reports (2016)
-
Social density processes regulate the functioning and performance of foraging human teams
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.