Abstract
The phenomenon of chimera states in the systems of coupled, identical oscillators has attracted a great deal of recent theoretical and experimental interest. In such a state, different groups of oscillators can exhibit coexisting synchronous and incoherent behaviors despite homogeneous coupling. Here, considering the coupled pendula, we find another pattern, the so-called imperfect chimera state, which is characterized by a certain number of oscillators which escape from the synchronized chimera's cluster or behave differently than most of uncorrelated pendula. The escaped elements oscillate with different average frequencies (Poincare rotation number). We show that imperfect chimera can be realized in simple experiments with mechanical oscillators, namely Huygens clock. The mathematical model of our experiment shows that the observed chimera states are controlled by elementary dynamical equations derived from Newton's laws that are ubiquitous in many physical and engineering systems.
Similar content being viewed by others
Introduction
Chimera states correspond to the spatiotemporal patterns in which synchronized and phase locked oscillators coexist with desynchronized and incoherent ones1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,19. Dynamically, it represents a sort of spatially extended symmetry breaking which develops in networks of identical oscillators, surprisingly without any evidence of asymmetry or external perturbation. Furthermore, this surprising hybrid behavior obeys a substantial reserve of robustness surviving at different kind of perturbations9. The experimental proof of chimeras' existence has only recently been provided for optical20, chemical21, mechanical22 and electronic18 systems.
Here, we show that other pattern, the so-called imperfect chimera state, which is characterized by a certain, small number of oscillators (solitary states23) which escape from the synchronized chimera's cluster or behave differently than the most of uncorrelated pendula can be observed in the networks of identical oscillators. As a proof of concept we use the network of coupled Huygens clocks24, i.e., the system of coupled pendula which are excited by the escapement clock's mechanism25,26.
We consider the system of n pendula which hung from the unmovable disc as shown in Figure 1(a). Pendula of length l and mass m are coupled through the linear spring with stiffness coefficient kx and linear dampers with damping coefficient cx. Pendula's displacements are given by the angles φi. Springs and dampers are connected to each pendulum at distance ls from the pivot. Each pendulum is connected with the nearest neighbor (green spring) and the second nearest neighbor (red springs). Additionally, the motion of each pendulum is damped by the linear damper characterized by damping coefficient cφ. The pendula are excited by the escapement mechanism which for φI > γN generate excitation torque MN25,26. This system can be implemented experimentally using the metronomes with the pendula connected by the spring elements as shown in Figure 1(b). The metronomes' parameters and details about coupling and measurements are given in the Methods.
The dynamics of the system of Figure 1(a) can be analyzed using the equations of motion which are derived from Newton's laws of dynamics (see Methods). We present the results for two different coupling schemes, (i) each pendulum is coupled with the nearest neighbor (local coupling), (ii) each pendulum is coupled with two nearest neighbors (nonlocal coupling).
Results
Numerical simulations show that the state of complete synchronization of all pendula co-exists with the state of phase synchronization in which there exists the constant phase shift between neighboring pendula and various chimera states illustrated in Figure 2(a–d). Left and right plots present respectively snapshots and time (t = NT, where N = 1,2,…) evolutions of n = 100 pendula. Typical chimera states obtained for the same parameters' values but different initial conditions (see Methods) are shown in Figure 2(a–d). Figure 2(a) presents one-headed chimera in which the cluster of the synchronized pendula co-exists with the cluster of pendula which are at rest (chimera death19). In Figure 2(b) one can observe two clusters of synchronized pendula which are separated by the groups of pendula at rest (two-headed chimera state). The synchronized clusters are in the anti-phase to each other.
Snapshots and time (t = NT, where N = 1,2,…) evolutions of chimera states of system (1), m = 1.0, l1 = g/4π2 = 0.2485 (i.e., the period of uncoupled pendulum is equal to T = 1.0), cφ = 0.01, MN = 0.0375, γN = 10° (escapement mechanism generates oscillations of uncoupled pendulum with amplitude A ≈ 0.25rad ≈ 15°), cx = 0.075 [Ns/m], (a–c) local coupling; kx = 0.25 [N/m], nonlocal coupling; kx = 0.125 [N/m], (a) perfect one headed chimera state, (b) perfect two headed chimera state, (c) imperfect chimera state, (d) imperfect chimera state, (during the time evolution the position of the particular pendula moves along the blue intervals shown at the snapshots).
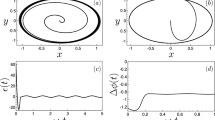
In Figure 2(c,d) we observe imperfect chimera states in which a small number of pendula behave differently to other pendula. Notice pendulum 9 in Figure 2(c). It oscillates periodically with different frequency than the pendula in the synchronized cluster. The phase portrait and frequency spectrum of this pendulum shown in Figure 3(a) indicate period 7 motion. Neighboring pendula, e.g. pendulum 10 behaves chaotically as can be predicted from Figure 3(b). The largest Lyapunov exponent estimated from time series is equal to 0.02.
Phase portraits and frequency spectra of pendula 9 - (a) and 10 - (b) during the imperfect chimera state of Figure 2(c).
To confirm experimentally the existence of imperfect chimera states we consider the set of 20 metronomes coupled as shown in Figure 1(b). We use Wittner Maelzel metronomes (Model No. 802K) covering a frequency range of 40 (largo) to 208 (prestissimo) tics per minute, with a standard deviation of relative frequencies of ~1%. When fully wound up, each metronome ticks for a duration of ~25 min (depending on the adjusted frequency), corresponding to ~1,500 oscillation cycles. In our experiment the frequency of each metronomes has been set to 200 tics per minute. To explore the complex behavior of the coupled metronomes quantitatively we measure the angular displacement of metronomes' pendula φi. The results of our experiments are summarized in Figure 4(a–g). For nonzero spring coupling, kx > 0, we observe a broad range of parameters in which imperfect chimeras (Figure 4(a–c,g)) and Movies S1 and S2) emerge both for local and nonlocal coupling. The procedure of generating chimera states is described in Methods. The example of imperfect chimera is shown in Figure 4(a–c) and the phase displacements of individual oscillators are illustrated in Figure 4(g). The group of metronomes at the background of Figure 4(a) is synchronized. Their escapement mechanisms are switched on and they oscillate with the frequency equal to the nominal frequency of 200 tics per minute. The metronomes on the first plane of Figure 4(a) are either at rest or oscillate with smaller amplitudes. The escapement mechanisms of most of them are permanently switched off but metronome 15 (see Figure 4(c)) oscillates with larger amplitude and different frequency (approximately 23 tics per minute). Its escapement mechanism is intermittently switched on. The yellow arrows in Figure 4(b,c) indicate the actual positions of the pendula (snapshot). The imperfect chimera states coexist with the state of complete (Figure 4(d)) and phase (Figure 4(e)) synchronization and perfect chimeras (Figure 4(f)). Imperfect chimera states are easily observed for both local and nonlocal coupling and the wide range of initial conditions (moreover, in our experiment it is easier to observe imperfect chimera states than the perfect ones).
(a) imperfect chimera state, the metronomes at the foreground of the photo are at rest or oscillate with a small amplitude (their escapement mechanisms are switched off), the metronomes at the background are synchronized, metronome 15 oscillates with different period than the rest of metronomes, its escapement mechanism is intermittently switched on, (d–g) experimental snapshots of pendula's displacements, (d) compete synchronization of all metronomes, (e) phase synchronization with the phase shift equal to 2π/20, (f) perfect chimera state, metronomes 3–12 are either at rest or oscillate with small amplitudes (during the time evolution they move along the blue intervals), (g) imperfect chimera state, metronomes 4 and 11 oscillate with different period (during the time evolution they move along the blue intervals).
The plots of the metronomes' displacements φi at the time when the first metronome has the largest positive displacement are shown in Figure 4(d–g). Figure 4(d) presents the state of complete synchronization. Synchronized metronomes oscillate with frequency ω = 1[s−1] (period equal to 2π) and constant amplitude approximately equal to 0.25. The phase synchronization with the phase shifts between pendula equal to 2π/20 is shown in Figure 4(b) (traveling wave moving around the ring). The perfect chimera state is presented in Figure 4(c). Pendula 1,2 and 13–20 are synchronized. Pendula 3–12 are either at rest or oscillate irregularly with small amplitudes (during the time evolution they move along the blue intervals). Figure 4(d) illustrates the state of imperfect chimera. As in the previous case pendula 1,2 and 13–20 are synchronized. The pendula of metronomes 4 and 11 oscillate with different period (7 times larger). Metronomes 3,5,10 and 12 demonstrate chaotic behavior (irregular behavior of these pendula is clearly visible in Movies S3).
Note that chimera states can be related to the driven intrinsic localized modes, i.e., highly localized responses to a spatially extended harmonic driving force observed in one-dimensional periodic lattices of oscillators28,29. The appearance of the driven intrinsic localized mode in the network of coupled oscillators29 is a qualitatively similar phenomenon as the creation of the solitary state24 and can lead to the formation of a chimera state in system (1). However, the imperfect chimera state which we have discovered is a completely new phenomenon where solitary oscillators appear within the chimera state and can demonstrate chaotic dynamics.
Typically, chimera states are observed in the networks of nonlocally coupled nodes. In system (1) they can be observed for both local and nonlocal cases. We use the examples of local and nonlocal coupling to show that in both cases the observed phenomena are qualitatively the same.
In summary we have constructed the simple experimental setup to explore the spatio-temporal dynamics of the network of the coupled pendula. The nodes in the network are locally and nonlocally coupled pendula (Huygens' clocks realized by metronomes). We observe the formation of coexisting coherent and incoherent domains in which the newly discovered pattern of imperfect chimera state is the most typical one. This behavior is observed experimentally and confirmed in numerical simulations.
Methods
The dynamics of the system of coupled pendula shown in Figure 1(a) is given by:

where i = 1,2,…,n, φ0 = φn, φn + 1 = φ1. System (1) is symmetrical on the ring, i.e., pendulum i is coupled with pendula i + 1 and i − 1 (local coupling) and in addition, with i − 2 and i + 2 (nonlocal coupling).
Numerical simulations: We used the following parameter values: m = 1.0, l1 = g/4π2 = 0.2485 (i.e., the period of uncoupled pendulum is equal to T = 1.0), cφ = 0.01, MN = 0.0375, γN = 10° (the escapement mechanism generates oscillations of the uncoupled pendulum with amplitude A ≈ 0.25rad ≈ 15°), cx = 0.075 [Ns/m], kx = 0.25 [N/m] (the case of local coupling (Figure 2(a–c))) and kx = 0.125 [N/m] (the case of nonlocal coupling (Figure 2(d))). The initial conditions are given by angle β0i describing the phase of pendulum oscillations, i.e., the initial pendula's displacements and velocities are as follow:  (one headed chimera in Figure 2(a)),
(one headed chimera in Figure 2(a)),  (two headed chimera in Figure 2(b)),
(two headed chimera in Figure 2(b)),  (im-perfect chimeras of Figure 2(c,d)). Eqs (1) have been integrated by the 4th order Runge-Kutta method. The largest Lyapunov exponent has been calculated from time series obtained by the numerical integration of eq.(1). We use the method introduced by Wolf et al.27. (Direct calculation of Lyapunov exponents is impossible as eq.(1) is discontinuous due to the model of the escapement mechanism.)
(im-perfect chimeras of Figure 2(c,d)). Eqs (1) have been integrated by the 4th order Runge-Kutta method. The largest Lyapunov exponent has been calculated from time series obtained by the numerical integration of eq.(1). We use the method introduced by Wolf et al.27. (Direct calculation of Lyapunov exponents is impossible as eq.(1) is discontinuous due to the model of the escapement mechanism.)
Experimental visualization
Metronomes have been placed on two rings as shown in Figure 1(b). The inner ring has the radius of 0.43 [m] and the outer one the radius of 0.65 [m]. As the spring elements we use the rubber bands (with the cross section radius 0.0001 [m]) of the length 0.27 [m] connecting the nearest neighbors and 0.74 [m] connecting the second nearest neighbors. The estimated stiffness coefficient is equal to 5 [N/m].
To generate the chimera state we start from the state of complete synchronization when all metronomes oscillate with the same amplitude and phase while all escapement mechanisms are switched on. The system has been perturbed in such a way that the pendulum of one of the metronomes has been stopped in the vicinity of the equilibrium position so the escapement mechanism of this metronome has been switched off. In the case of strong coupling due to the energy transfer from the neighboring pendula25,26 this pendulum starts to oscillate and when its amplitude increases the value of γN, its escapement mechanism is switched on and after short transient time the system goes back to the state of complete synchronization (in our experiments for the spring elements of stiffness coefficient equal to 20[N/m] – local coupling and 10[N/m] – nonlocal coupling). For the case of smaller coupling (in our experiments for the spring elements of stiffness coefficient equal to 5[N/m])the perturbed pendulum starts to oscillate but its amplitude does not increase the value of γN and its escapement mechanism is not switched on. Due to the energy transfer to this pendulum the amplitudes of the neighboring pendula decrease and reach the values smaller than γN so their escapement mechanisms are switched off. The system is divided into two groups of synchronized metronomes with the escapement mechanisms permanently switched on and the metronomes which pendula oscillate with small amplitude or are at rest.
The set of coupled metronomes has been located in the dark room and has been lit by 3 ultraviolet lamps situated symmetrically around the rig at the distance of 2π/3. The ultraviolet light accentuated the image ends' tips installed on the metronomes' pendula in order to identify pendula's displacements on the photographs. The camera has been located on a rotating platform in the centre of the rig. Due to the long exposure time (1 s) to reduce the camera oscillations generated at the moment of shutter release we use the self-timer. Exposure time of 1 [s] allows the estimation of the pendula's amplitude as the trace of motion on the picture includes several periods of pendula's oscillations. At the end of the exposure the flash has been released which allows the identification of the specific position of the pendulum on the trace of oscillations.
Movie S1. General view of the state of imperfect chimera.
Movie S2. The state of imperfect chimera shown in ultraviolet light.
Movie S3. Irregular oscillations of a few metronomes.
References
Kuramoto, Y. Chemical Oscillations, Waves and Turbulence., (Springer, New York, 1984).
Kuramoto, Y. & Battogtokh, D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlinear Phen. Complex Syst. 5, 380–385 (2002).
Abrams, D. M. & Strogatz, S. H. Chimera states for coupled oscillators. Phys. Rev. Lett. 93, 174102 (2004).
Abrams, D. M., Mirollo, R., Strogatz, S. H. & Wiley, D. A. Solvable model for chimera states of coupled oscillators. Phys. Rev. Lett. 101, 084103 (2008).
Martens, E. A., Laing, C. R. & Strogatz, S. H. Solvable model of spiral wave chimeras. Phys. Rev. Lett. 104, 044101 (2010).
Motter, A. E. Nonlinear dynamics: Spontaneous synchrony breaking. Nature Phys. 6, 164–165 (2010).
Omelchenko, I., Maistrenko, Y. L., Hövel, P. & Schöll, E. Loss of coherence in dynamical networks: Spatial chaos and chimera states. Phys. Rev. Lett. 106, 234102 (2011).
Omelchenko, I., Riemenschneider, B., Hövel, P., Maistrenko, Y. L. & Schöll, E. Transition from spatial coherence to incoherence in coupled chaotic systems. Phys. Rev. E 85, 026212 (2012).
Laing, C. R. The dynamics of chimera states in heterogeneous Kuramoto networks. Physica D 238, 15691588 (2009).
Laing, C. R. Chimeras in networks of planar oscillators. Phys. Rev. E 81, 066221 (2010).
Laing, C. R. Fronts and bumps in spatially extended Kuramoto networks. Physica D 240, 1960–1971 (2011).
Martens, E. A. Bistable chimera attractors on a triangular network of oscillator populations. Phys. Rev. E 82, 016216 (2010).
Martens, E. A. Chimeras in a network of three oscillator populations with varying etwork topology. Chaos 20, 043122 (2010).
Wolfrum, M. & Omel'chenko, O. E. Chimera states are chaotic transients. Phys. Rev. E 84, 015201 (2011).
Sethia, G. C., Sen, A. & Atay, F. M. Clustered chimera states in delay-coupled oscillator systems. Phys. Rev. Lett. 100, 144102 (2008).
Sen, A., Dodla, R., Johnston, G. L. & Sethia, G. C. in Understanding Complex Systems. (ed. Atay F. M.) 141 (Springer, 2010).
Waller, I. & Kapral, R. Spatial and temporal structure in systems of coupled nonlinear oscillators. Phys. Rev. A 30, 20472055 (1984).
Zakharova, A., Kapeller, M. & Scholl, E. Chimera death: Symmetry breaking in dynamical networks. Phys. Rev. Lett. 112, 154101 (2014).
Hagerstrom, A. M. et al. Nature Physics 8, 658 (2012).
Tinsley, M. R., Nkomo, S. & Showalter, K. Nature Physics 8, 662 (2012).
Martens, E. A., Thutupalli, S., Fourriere, A. & Hallatschek, O. Proc. Nat. Acad. Sciences 110, 10563 (2013).
Larger, L., Penkovsky, B. & Maistrenko, Y. L. Phys. Rev. Lett. 111, 054103 (2013).
Maistrenko, Yu., Penkovsky, B. & Rosenblum, M. Solitary state at the edge of synchrony in ensembles with attractive and repulsive interaction. Phys. Rev. E 89, 060901(R) (2014).
Huygens, C. [Letter to de Sluse]. Oeuveres Completes de Christian Huygens. (letters; no. 133 of 24 February 1665, no. 1335 of 26 February 1665, no. 1345 of 6 March 1665), (Societe Hollandaise DesSciences, Martinus Nijhor, La Haye, 1665).
Kapitaniak, M., Czolczynski, K., Perlikowski, P., Stefanski, A. & Kapitaniak, T. Synchronization of clocks. Phys. Rep. 517, 1–67 (2012).
Czolczynski, K., Perlikowski, P., Stefanski, A. & Kapitaniak, T. Clustering and Synchronization of Huygens' Clocks. Physica A 388, 5013–5023 (2009).
Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. Determining Lyapunov exponents from a time series. Physica D 16, 285–317 (1985).
Rossler, T. & Page, J. B. Intrinsic localized modes in driven anharmonic lattices with realistic potentials. Phys. Lett. A 204, 418–426 (1995).
Basu Thakur, R., English, L. Q. & Sievers, A. J. Driven Intrinsic Localized Modes in a Coupled Pendulum Array. J. Phys. D: Appl. Phys. 41, 015503 (2008).
Acknowledgements
We thank B. Jagiello for the technical assistance in the experiments and M. Wojewoda for producing photographs and movies. This work has been supported by the Foundation for Polish Science, TEAM Programme -- Project No TEAM/2010/5/5 and by the Polish National Science Centre, MAESTRO Programme - Project No 2013/08/A/ST8/00/780.
Author information
Authors and Affiliations
Contributions
Yu.M. and T.K. initiated this work, P.K. and K.C. performed the modeling and simulations, K.C. and T.K. designed the experiment, J.W. build experimental set up and performed experiments. P.K., J.W., K.C., Yu.M. and T.K. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Kapitaniak, T., Kuzma, P., Wojewoda, J. et al. Imperfect chimera states for coupled pendula. Sci Rep 4, 6379 (2014). https://doi.org/10.1038/srep06379
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06379
This article is cited by
-
Weakly nonlinear analysis on synchronization and oscillation quenching of coupled mechanical oscillators
Scientific Reports (2024)
-
Chimera patterns in conservative Hamiltonian systems and Bose–Einstein condensates of ultracold atoms
Scientific Reports (2023)
-
Synchronization patterns in heterogeneous ensembles of coupled pendula
Indian Journal of Physics (2023)
-
Mathematical Framework for Breathing Chimera States
Journal of Nonlinear Science (2022)
-
Collective Dynamics and Bifurcations in Symmetric Networks of Phase Oscillators. II
Journal of Mathematical Sciences (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.