Abstract
Nash equilibrium is widely present in various social disputes. As of now, in structured static populations, such as social networks, regular and random graphs, the discussions on Nash equilibrium are quite limited. In a relatively stable static gaming network, a rational individual has to comprehensively consider all his/her opponents' strategies before they adopt a unified strategy. In this scenario, a new strategy equilibrium emerges in the system. We define this equilibrium as a local Nash equilibrium. In this paper, we present an explicit definition of the local Nash equilibrium for the two-strategy games in structured populations. Based on the definition, we investigate the condition that a system reaches the evolutionary stable state when the individuals play the Prisoner's dilemma and snow-drift game. The local Nash equilibrium provides a way to judge whether a gaming structured population reaches the evolutionary stable state on one hand. On the other hand, it can be used to predict whether cooperators can survive in a system long before the system reaches its evolutionary stable state for the Prisoner's dilemma game. Our work therefore provides a theoretical framework for understanding the evolutionary stable state in the gaming populations with static structures.
Similar content being viewed by others
Introduction
In the past half century, the concept of Nash equilibrium is widely accepted and applied to analyze the possible outcomes in game theory if several strategists are making decisions at the same time. Their applications on arms races1, currency crises, environmental regulations2, auctions, even football matches3 are well known. In the evolutionary game theory4,5,6, Nash equilibrium5,6,7 actually is a stable mixed strategy. The mixed strategy represents a distribution of pure strategies in the evolutionary stable state. Indeed, this class of Nash equilibrium is composed of all the individuals. Instead, in the classical two-person two-strategy games, Nash equilibrium is only composed of two individuals. The Nash equilibrium is interpreted as that once two individuals are in this equilibrium, they can not gain more payoff by adjusting their own pure strategy unilaterally.
In a structured population as social networks, individuals don't normally interact with strangers. Their opponents are relatively stable, which are called neighbors in complex networks8,9,10,11. In this scenario, a new strategy equilibrium emerges in the system, which unevenly exists in two connected individuals with other neighbors. We define this class of strategy equilibrium as a local Nash equilibrium. In this paper, we present an explicit definition of the local Nash equilibrium in networks for the two-strategy games12,13,14,15,16. We investigate the condition that a system reaches the evolutionary stable state. For the Prisoner's dilemma game (PDG)17,18,19,20,21,22,23 and snow-drift game (SG)4,5,24,25, we will show that the Local Nash equilibrium is a typical feature of the cooperative structured populations.
In a structured population, the equilibrium between two strategies is actually composed of the two strategists and all their other neighbors. The change on the strategy equilibrium leads to a completely different evolutionary stable state4. This evolutionary stable state is composed of a set of strategies with different frequencies. The frequencies of the strategies in this state must be statistically stable. In the evolutionary stable state of the games with cooperators and defectors, the frequency of cooperators in the structured populations has attracted a lot of attention12,13,24,26,27,28. Researchers are interested in how the cooperators can survive in a circumstance with a large temptation to defect. To clarify this point, one has to understand the generation of the evolutionary stable state at first.
In the evolutionary game theory, previous studies discussed the evolutionary stable state in the unstructured populations from a replicator dynamics perspective6,29,30,31. In the structured populations, for example, spatial24,26 and social12,13,27,28 networks, because of the difficulty of formulating the replicator dynamics, the discussions are relatively restricted. In the structured populations except the fully connected population, the folk theorem of evolutionary game theory does not stand6, since the strategy equilibrium only exists locally. To get the evolutionary stable state, there is no need to get all the connected individuals in the local Nash equilibrium. A certain number of the local Nash equilibrium suffice to lead the system into the stable state, since balancing the gap of payoffs between different strategies is not so difficult in the structured populations. In what follows, we will discuss what the local Nash equilibrium in structured populations is. We will present extensive numerical evidences that it is a typical feature of cooperative populations.
Local Nash equilibrium
In a structured population, such as the spatial networks24,26, random graphs (network)32, Watts and Strogatz small-world networks (WS)32 and Barabási and Albert scale-free networks (BA)33, an individual normally plays with its nearest neighbors in one round. The links among them are relatively stable in the whole evolution process. In one round, a game is played by every pair of individuals connected by a link. For an individual i, it plays with ki neighbors, where ki = Σj Aij denotes i's degree or connectivity. Aij is an entry of the adjacency matrix of the network, taking values Aij = 1 (i = 1, 2, …, N) whenever node i and j are connected and Aij = 0 otherwise.
In a two-strategy evolutionary game, we define i's strategy as

Xi(n) can only take 1 or 0 at the nth round. For Xi(n) = 1, i is a cooperator denoted by C. For Xi(n) = 0, i is a defector denoted by D.
For i's local gaming environment, we define i's local frequency of C at the nth round as

In this scenario, keeping i's neighbors' strategies unchanged is equivalent to keeping Wi(n) unchanged. For the global gaming environment, we define the global frequency of C at the nth round as

where N denotes the size of network. We take the PDG4,5 for example. As a heuristic framework, the PDG describes a commonly identified paradigm in many real-world situations. It has been widely studied as a standard model for the confrontation between cooperative and selfish behaviors. The selfish behavior here is manifested by a defective strategy, aspiring to obtain the greatest benefit from the interaction with others. This PDG game model considers two prisoners who are placed in separate cells. Each prisoner must decide to confess (defect) or keep silence (cooperate). A prisoner may receive one of the following four different payoffs depending on both its own strategy and the other prisoner's strategy. It gains T (temptation to defect) for defecting a cooperator, R (reward for mutual cooperation) for cooperating with a cooperator, P (punishment for mutual defection) for defecting a defector and S (sucker's payoff) for cooperating with a defector. Normally, the four payoff values follow the following inequalities: T > R > P ≥ S and 2R > T + S. Here, 2R > T + S makes mutual cooperation the best outcome from the prospective of the interest of these two-person group.
In the PDG, the payoff table is a 2 × 2 matrix. Considering equation (1), i's payoff at the nth round reads as

Given equation (2), Σj AijΩj(n) can be rewritten as

Insert equation (1) and equation (5) into equation (4), we have

where ki denotes the individual i's degree or connectivity. Δi(n) = S − P + (R − T + P − S)Wi(n), where Wi(n) denotes i's local frequency of C at the nth round.
The maximum of Gi(n) can be obtained by the best strategy, which is denoted by

If two connected individuals i and j choose Xi,max(n) and Xj,max(n) as their strategies at the nth round, respectively, the individual i and j are in a special situation, which is defined as the local Nash Equilibrium. We call these two individuals “Nash pair”. If all the individuals in the system are in the local Nash Equilibrium, we define that these individuals are in a global Nash Equilibrium. If Δi(n) = 0 or Δj(n) = 0, this local equilibrium is classified as a weak local Nash equilibrium. Otherwise, it is classified as a strict local Nash equilibrium. Note that the local Nash equilibrium defined here is not a mixed strategy but a pure strategy's local combination. The mixed strategy, instead, represents the distribution of pure strategies in the population.
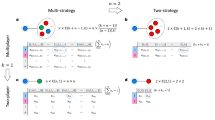
Notably, not only two D players can form a Nash pair, C and D or two C can also form a Nash pair under a proper condition. Five typical examples are shown in Fig. 1. In this scenario, we define

where Nω denotes the number of the Nash pairs in a network and E denotes the number of edges in the network. In another word, α represents the fraction of Nash pairs in the connected individuals. When ki = kj = 1, the local Nash equilibrium is equal to Nash equilibrium in the classical game theory. In the following, we will show that α can be considered as a tool to judge whether the evolutionary system is in an evolutionary stable state.
Illustrations of Nash pairs for the PDG and SG.
The two individuals in the yellow eclipses form a Nash pair. For the PDG, the sequence of payoffs follows T > R > P ≥ S. (a-1) shows a defector-defector Nash pair, where Δi(n) = Δj(n) < 0; (a-2) shows a defector-cooperator Nash pair, where Δi(n) < 0 and Δj(n) = 0; For the SG, the sequence of payoff changes to T > R > S ≥ P. (b-1) shows a cooperator-cooperator Nash pair, where Δi(n) = Δj(n) > 0 for S − P > 7(T − R). (b-2) shows a cooperator-defector Nash pair, where Δi(n) ≥ 0 and Δj(n) < 0. (b-3) shows a defector-defector Nash pair, where Δi(n) = Δj(n) < 0 for S − P < 7(T − R).
Results
In the well-mixed population, everybody interacts with everybody else with an identical probability. The system reaches the evolutionary stable state when all the defectors are in Nash equilibrium, in which no cooperators can survive5,31. But, real populations are not well mixed. Some have an explicit social12,13,27,28 or spatial properties24,26. In these populations, a large number of previous studies12,13,24,26,27,28 concentrated on explaining why the cooperators can survive in the evolutionary stable state. For a population with a fixed topological structure and updating rule, various cooperative patterns are generated by different initial conditions and randomness. When the updating rule is deterministic, the system is rather sensitive to the initial condition, which can thus be regarded as a topological chaos26 in a sense. In the evolution process, β, the frequency of cooperators in the network, fluctuates dramatically. In terms of β, one can hardly predict whether it will decay to 0 before the system is stable. The evolutions of β in different systems exhibit different pictures. However, these systems have one feature associated with α in common.
Global and local Nash equilibrium
In the structured population, α keeps evolving with time. If α grows with time, the system is approaching the global Nash equilibrium. If α reaches 1, the system reaches the global Nash equilibrium, where all the defectors are in Nash pairs. In this scenario, no cooperators can survive. If α decays with time, the payoff of the individuals with Xmax(n) grows, since the restriction from their neighbors with Xmax(n) decays. The system reaches its evolutionary stable state until their payoffs are close to their neighbors' payoffs.
To further understand the evolution process of the gaming system, we trace the evolution process of the Nash pairs in the PDG. Interestingly, once α decays with time, the cooperators can always survive in the evolutionary stable state. The system gets relatively stable when α reaches its minimum. One can find that Δ (n) ≤ 0 in equation (7), since T > R > P ≥ S. This ranking of the game parameters indicates that the Nash pairs in the PDG is either a defector-defector pair or a defector-cooperator pair. As mentioned above, the formation of the defector-defector Nash pair limits the payoff of these defectors. Thus these defector-defector Nash pairs become a breakthrough of their cooperative neighbors. This is why we can predict the existence of cooperators in the evolutionary stable state by the fraction of Nash pairs, since the number of defectors normally decays with time when the Nash pairs are invaded.
Clearly, this way can hardly be generalized to other games. For instance, there is no direct connection between the number of defectors and α in the snow-drift game (also known as the hawk-dove or chicken game)4,5,24,25, thus one can not predict the existence of cooperator by α any more. However, one can still identify the evolutionary stable state by α.
Numerical experiments
To confirm our conclusion above, we test two typical updating rules on two classes of typical social networks. The first updating rule is proposed by Nowak and May26, while the second one is proposed by Karl H. Schlag34. Since Santos and Pacheco find that the second updating rule can highly promote cooperation in the networks with a power-law degree distribution27,35,36, the rule is extensively employed in the following works28,35,36,37,38,39. In terms of topological structures, we choose the well-known Watts and Strogatz (WS) small-world networks32 and Barabási and Albert (BA) scale-free networks33. The details about the updating rules, network models and simulation settings are shown in section Methods.
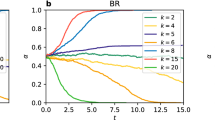
In Fig. 2 and 3, we measure the average of α and β over extensive simulations. All the networks are composed of 1, 024 identical individuals with average degree 6. We run ten simulations for each of the parameter values for the game on each of the ten networks. Thus, each plot in the figures corresponds to 100 simulations. For the PDG, in Fig. 2, one can observe the decay of α for the temptation to defect T < 1.5 in (a), T < 1.3 in (b), T ≤ 2.0 in (c) and T ≤ 2.0 in (d) (T is an entry of the payoff matrix in equation 4). In these cases, our simulation results show that cooperators can survive in the corresponding evolutionary stable states. For the SG, in Fig. 3, for the simulation parameter r < 1, the systems get their evolutionary stable state when α decays to its minimum. Instead, for r = 1, one can derive T = 1, R = 0.5, S = P = 0, since P = 0,  ,
,  and
and  . Given Δi(n) = S − P + (R − T + P − S)Wi(n), one can derive Δi(n) = −0.5Wi(n) ≤ 0. Thus, Xi,max(n) = 0 is a solution of equation 7 when Wi(n) = 0. If and only if r = 1 and Wi(n) = 0, the systems can reach the global Nash equilibrium, where the defectors dominate the population.
. Given Δi(n) = S − P + (R − T + P − S)Wi(n), one can derive Δi(n) = −0.5Wi(n) ≤ 0. Thus, Xi,max(n) = 0 is a solution of equation 7 when Wi(n) = 0. If and only if r = 1 and Wi(n) = 0, the systems can reach the global Nash equilibrium, where the defectors dominate the population.
The evolution of  and
and  for the PDG in social networks.
for the PDG in social networks.
We measure the evolution of α and β for a series of the temptation to defect T = 1.1, 1.2, …, 2.0. The other parameters of the PDG are set as P = S = 0 and R = 1. (a) and (c) show the simulation results obtained by the updating rule proposed by Nowak and May26 on the WS small-world networks and BA scale-free networks, respectively. (b) and (d) show the simulation results obtained by the updating rule proposed by Santos and Pacheco27 on both networks, respectively. Note that (a), (b), (c) and (d) are semilog graphs. For (e), (f), (g) and (h), we show the average frequency of cooperators  (dotted lines) and distribution of frequencies of cooperators for each value of T (the squares with gray scale are used to describe the value of β distribution), corresponding to (a), (b), (c) and (d). These squares are the binned data of β. For example, a decimal in (0.25, 0.34) is approximated with 0.3.
(dotted lines) and distribution of frequencies of cooperators for each value of T (the squares with gray scale are used to describe the value of β distribution), corresponding to (a), (b), (c) and (d). These squares are the binned data of β. For example, a decimal in (0.25, 0.34) is approximated with 0.3.
The evolution of  and
and  for the snow-drift game in social networks.
for the snow-drift game in social networks.
We keep the same simulation parameter r as that in the reference24. r is a parameter controlling the level of the temptation to play D. We test the cases of r = 0.1, 0.2, …, 1.0. The four payoff parameters are set as P = 0,  ,
,  and,
and,  . The other the simulation settings are the same as Fig. 2.
. The other the simulation settings are the same as Fig. 2.
Temporary and permanent evolutionary stable state
Naturally, we come back to a key issue, ‘Why do we choose the Nash pairs to judge the evolutionary stable state?’ In terms of the current criteria12,13,24,26,27,28, it seems to be, in a sense, ambiguous. We currently rely on measuring the fraction of cooperators (or defectors) to check whether it is stabilized at a particular value with minimum fluctuation. This method may lead to a misleading conclusion in some conditions. For instance, β may be stabilized at a particular value with a small fluctuation before the system reaches the evolutionary stable state.
In Fig. 4, one can observe two long temporary stable states in the black rectangles. The previous definition in the literatures may take them as a permanent evolutionary stable state. This drawback originates from that the definition can hardly tell the difference between the temporary stable state and permanent stable state in few time steps. From the prospective of the local Nash equilibrium, it is clear that the system doesn't reach its evolutionary stable state, since α neither reaches its maximum 1 nor decays with time. This state conflicts with the polarized feature of α. In another word, α can only be stabilized at the maximum 1 or a certain minimum. If cooperators can survive in the system, one should observe that the Nash pairs are invaded by the cooperators and α decays with time. After the system reaches its evolutionary stable state, α would be stabilized at its minimum with a slight fluctuation. If not, α is growing with time to 1.
Comparison between the evolution processes of α and β in a single simulation for T = 1.2 of the PDG and r = 0.8 of the SG.
In this figure, the cyan and black solid lines denote the simulation results obtained by the updating rule proposed by Nowak and May26 on the WS small-world networks and BA scale-free networks, respectively. The olive and red solid lines denote the simulation results obtained by the updating rule of Santos and Pacheco27 on both networks, respectively. Note that α doesn't reach 1 or decays with time before entering the black rectangles, while β is stabilized at a certain value. This observation indicates the system doesn't reach its evolutionary stable state. On the other hand, one can observe that the green solid line in (a) is still decaying at the time step 51, 000, which indicates the cooperators is growing after the time step 51, 000. These conclusions can hardly be obtained by the observations in (b). For SG, we can't predict whether cooperators can survive in the systems by α, but we can still judge whether the systems reach their evolutionary stable states by it. In (d), one can observe the cyan, black and olive lines become rather stable when α reaches its minimum in (c). One can also observe that the red line in (c) decays slowly at the end of our simulation, which indicates the system is still evolving. These ‘long temporary stable states’ observed in (b) and (d) originate from the topological feature of scale-free networks. Once an individual with a large degree changes his/her strategy, β will vary drastically36,40.
In addition, the evolution of α also provides a general way to measure the self-organizing ability of the system in another sense. The ability is governed by the strategy updating rule. In the semilog graph Fig. 2(a) and (c) (Nowak and May's rule), one can observe that the decay rate of α is much higher than that in Fig. 2(b) and (d) (Santos and Pacheco's rule). If one takes the evolutionary rate as the self-organizing ability of system, this observation indicates that the self-organizing ability of system governed by Nowak and May's updating rule is much higher than that governed by Santos and Pacheco's rule.
Briefly, the local Nash equilibrium is a typical feature of evolutionary games in the structured populations. In a unstructured population, the system can reach its evolutionary stable state only if everyone defects. In a structured population, the local Nash equilibrium can also lead the system to its evolutionary stable state. This feature finally differs the evolutionary games in the structured populations from that in the unstructured populations. For the PDG, it has an extra application, which can help to predict the tendency of evolution before the system reaches its stable state.
To clarify the connection between the local Nash equilibrium and the system stability, we discuss the function of the Nash pairs. For convenience, we define

where DΩ denotes the number of defectors in Nash pairs in a network and ND denotes the number of defectors in the network. In another word, γ represents the fraction of defectors in the local Nash equilibrium. Fig. 5 shows the evolution process of γ in the PDG. For the two classes of networks, (a) and (b) show the cases of T = 1.2 for the WS small-world networks, (c) and (d) show the cases of T = 1.9 for the BA scale-free networks, both of which are not dominated by cooperators (red plots) or defectors (blue plots). One can observe that almost all the defectors (blue plots in the second row) are in the Nash pairs (yellow plots in the third row). This observation indicates almost all the defectors are in the local Nash equilibrium, which confirms the observations in the panels shown in the first row.
The evolution of γ for the PDG.
The first row shows the evolution process of γ. The second row shows the roles of individuals at step 10, 001. The third row highlights the defectors in Nash equilibrium, corresponding to the second row. Column (a) and (c) show the simulation results obtained by a updating rule proposed by Nowak and May26 on the WS small-world networks and BA scale-free networks, respectively. Column (b) and (d) show the simulation results obtained by the updating rule of Santos and Pacheco27 on both networks, respectively. In this figure, solid red circles denote the cooperators, blue circles denote the defectors and yellow circles denote the defectors in the local Nash equilibrium. In column (a) and (b), T = 1.2. In column (c) and (d), T = 1.9.
Fig. 6 shows the evolution process of γ in the SG. One can observe that γ is neither close to 1 nor 0, which indicates that SG is a co-existence dilemma41. Comparing the second row with the third row, one can find that the two individuals in the local Nash equilibrium can be two cooperators, two defectors and one cooperator and one defector. This feature of the local Nash equilibrium is clearly different from the classical Nash equilibrium in the SG.
The evolution of γ for the SG.
The first row shows the evolution process of γ. The second row shows the roles of individuals at step 10, 001. The third row highlights the defectors in Nash equilibrium, corresponding to the second row. Column (a) and (c) show the simulation results obtained by a updating rule proposed by Nowak and May26 on the WS small-world networks and BA scale-free networks, respectively. Column (b) and (d) show the simulation results obtained by the updating rule of Santos and Pacheco27 on both networks, respectively. In this figure, solid red circles denote the cooperators, blue circles denote the defectors and yellow circles denote the defectors in the local Nash equilibrium. In this figure, the simulation parameter r is uniformly set to 0.8.
In addition to these two classes of networks and two updating rules discussed above, we also test the influence of other topological structures on the function of Nash pairs for the PDG. We run extensive simulations on random graphs32, regular graphs and regular lattices. All the observations are consistent with the results we show here (see the supplementary information for details).
Discussion
Inspired by the Nash equilibrium in the classical game theory, we have presented an explicit definition of local Nash equilibrium in structured populations. Here, we add the word ‘local’ to emphasize that the Nash equilibrium mentioned in this paper is in the structured populations. The local Nash equilibrium proposed in this paper is an extension of the Nash equilibrium in the classical game theory, shown in Fig. 7(a). Briefly, if both two connected individuals can not gain more payoff by adjusting their pure strategies when their neighbors' strategies are fixed, they are in the local Nash equilibrium, shown in Fig. 7(c). For convenience, we call these two individuals “Nash pair”. Notably, the local Nash equilibrium is not directly relevant to the updating rules, since it is based on the local pattern of pure strategies.
Illustrations of Nash equilibrium for the PDG in (a) two persons, (b) unstructured population and (c) structured population.
The individuals in the yellow eclipses are in the different types of Nash equilibrium. Solid lines denote the real links in the structured populations, while dotted lines denote the possible links in the unstructured populations. The classical two-person game shown in (a) is the simplest structured population, where ki = kj = 1 and the size of network equals 2.
Based on the definition of the local Nash equilibrium, we observe that the local Nash equilibrium is a typical feature of the cooperative structured populations. Unlike in the unstructured population, this concept is not built on the replicator dynamics6, since the mixed strategy7 is normally not allowed in the structured populations as of now. Even if the mixed strategy is allowed, the present updating rules can hardly be formulated as well. Although much efforts are devoted to formulate the updating rules, while the corresponding results are relatively limited42. On top of this, the Nash equilibrium in the unstructured populations is composed of all the individuals, shown in Fig. 7(b). This equilibrium is a global behavior, while it is a local behavior in the structured populations.
For the PDG, we accidentally find that once the fraction of Nash pairs in the connected individuals decays with time, cooperators can survive in its evolutionary stable state. If cooperators can survive in the system, the system reaches its evolutionary stable state when the fraction of Nash pairs reaches its minimum. In this scenario, one can find that the cooperative behavior is actually protected by these Nash pairs. The fact that almost all the defectors are in Nash pairs cuts these defectors' payoffs and enables cooperation to survive in a circumstance with a large temptation to defect. If the fraction of Nash pairs grows constantly, the system is approaching the global Nash equilibrium. From the prospective of the local Nash equilibrium, the emergence of the cooperative cluster actually originates from the self-organization of the Nash pairs, which confirms the previous explanation28 in a sense.
To check the influence of the network size, we also run extra simulations on the networks with 256, 4 196 and 16 384 individuals with respect to that the sizes must satisfy n2 ( ) in a regular lattice. We observe that the size of networks have an apparent influence on the value of α and β, while it doesn't change the evolution of Nash pairs, namely, growing to 1 or decaying to the minimum. In addition, we also test the influence of the payoff memory, defined in the references39,42. Again, the influence is confined to the level of cooperation. The Nash pairs can still be used to judge the system stability and predict the existence of the cooperative cluster. Unlike the smooth decay in Figs. 2 and 3, the number of Nash pairs decays suddenly when the payoff memory is large. Respecting the details of updating rules have a crucial influence on the result in structured population12,13,41, we also test the function of Nash pairs in the population governed by the ‘death-birth’ rule13 and Moran process12. For the ‘death-birth’ rule with a weak selection (the intensity of selection equals 0.01) and Moran process when all the link weights are identical, it is likewise valid. Acknowledgedly, there are many other interesting updating rules41,42, while we can't cover all of them in one paper. Our coming work probably can provide more evidences.
) in a regular lattice. We observe that the size of networks have an apparent influence on the value of α and β, while it doesn't change the evolution of Nash pairs, namely, growing to 1 or decaying to the minimum. In addition, we also test the influence of the payoff memory, defined in the references39,42. Again, the influence is confined to the level of cooperation. The Nash pairs can still be used to judge the system stability and predict the existence of the cooperative cluster. Unlike the smooth decay in Figs. 2 and 3, the number of Nash pairs decays suddenly when the payoff memory is large. Respecting the details of updating rules have a crucial influence on the result in structured population12,13,41, we also test the function of Nash pairs in the population governed by the ‘death-birth’ rule13 and Moran process12. For the ‘death-birth’ rule with a weak selection (the intensity of selection equals 0.01) and Moran process when all the link weights are identical, it is likewise valid. Acknowledgedly, there are many other interesting updating rules41,42, while we can't cover all of them in one paper. Our coming work probably can provide more evidences.
In a nutshell, the self-organization of Nash pairs forms the final dynamical complex patterns of evolutionary games in structured populations. The concept of the local Nash equilibrium provides a way to judge whether a gaming structured population reaches the evolutionary stable state. For the PDG, the concept can also be used to predict whether cooperation can exist in a system long before the system reaches its evolutionary stable state. In the evolutionary stable state, the minimal amount of local Nash equilibriums form the smallest interface between the pure strategy clusters. This may be the reason why the system exhibits a relatively stable state when the number of local Nash equilibrium reaches the minimum. Our observations provide a different prospective for understanding the evolutionary stable state in gaming structured populations. It may also help to analytically model the evolutionary games in structured populations.
Methods
Two-person two-strategy game
Two-person two-strategy game model is a heuristic framework, which describes a basic paradigm in many real-world situations. The well-known examples are the PDG17,18,19,20,21,42 and SG (also known as the hawk-dove or chicken game)4,5,24,25. The two-strategy game has been widely studied as a standard model for the confrontation between two different behaviors, for example, to cooperate or to defect. For convenience, the two strategies are denoted by C and D.
In a round of two prisoners' game, an individual i may receive one of the following four different payoffs depending on both its own strategy and the other individual j's strategy. With D, it gains T and P in the cases that j plays C and D, respectively. With C, it gains R and S in the cases that j plays C and D, respectively. For the PDG, C and D denote staying silent and betraying, respectively. In this scenario, the following condition must hold for the payoffs T > R > P ≥ S. For the snow-drift game, the sequence of payoff changes to T > R > S ≥ P. No matter which game the population plays, at the next round, all the individuals will know the strategy of their opponents in the previous round. They can then adjust their strategies simultaneously according to a certain updating rule of strategy.
Updating rules
The updating rules we adopt in this paper are Darwinian, but the ways to select a strategy with higher payoff are quite different. The first updating rule is proposed by Nowak and May26, which describes a local deterministic evolution. In this process, each individual chooses the neighbor gaining the highest payoff in the last round as its reference. If the payoff of the reference is higher than the individual, they will play the reference's strategy in the next round. Otherwise, it will keep its own strategy. The second updating rule27 describes a local random evolution. In one round, an individual i chooses a randomly picked neighbor j as its reference. If j's payoff is higher than that of i, i will play j's strategy in the next round with a probability directly proportional to the difference between their payoffs Gj − Gi and inversely proportional to Max{ki, kj} · T, where ki and kj denote the connectivity of i and j, respectively. T denotes the temptation to defect. Based on the previous definition12,13,24,26,27,28, an evolutionary game in structured populations continues until the system reaches a dynamical equilibrium, where the fraction of cooperators (or defectors) is stabilized at the particular value with minimum fluctuation.
Network models
We test two typical networks in this paper. One is the WS small world network32, while the other is the BA scale-free network33. The WS small-world networks are generated by randomly rewiring 10% of the links in the regular graph, which are composed of 1, 024 identical individuals of degree 6. The BA scale-free networks are generated by m0 = m = 333, where m0 denotes the size of the initial fully connected network and m denotes the number of links among a new node and the existing individuals in the network.
Simulation settings
The simulation results were obtained by ten random assignments of 512 defectors and cooperators on ten different realizations of the same type of network specified by the appropriate parameters. We run 11, 000 time steps for each simulation (except Fig. 4), in which 10, 000 steps to guarantee that the system is in a dynamical equilibrium in which the number of cooperators (or defectors) is stabilized at the particular value with minimum fluctuation. Next, we measure β from 10, 000 to 11, 000 steps to derive  .
.
References
Schelling, T. C. Elements of theory of strategy. The Strategy of Conflict. 74–77. (Harvard University Press, Cambridge, 1980).
Ward, H. Game Theory and the Politics of Global Warming: the State of Play and Beyond. Political Studies 44, 850–871 (1996).
Chiappori, P., Levitt, S. & Groseclose, T. Testing Mixed-Strategy Equilibria When Players Are Heterogeneous: The Case of Penalty Kicks in Soccer. American Economic Review 92, 1138–1151 (2002).
Smith, J. M. Evolution and the theory of games. American Scientist 64, 41–45 (1976).
Gintis, H. Game theory evolving: A Problem-Centered Introduction to Modeling Strategic Interaction. Journal of Economic Literature 39, 572–573 (2001).
Hofbauer, J. & Sigmund, K. Evolutionary game dynamics. Bulletin. (new series) of the american mathematical society 40, 479–519 (2003).
Nash, J. F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 36, 48–49 (1950).
Albert, R. & Barabási, A. L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
Dorogvtsev, S. N. & Mendes, J. F. F. Evolution of networks. Adv. Phys. 51, 1079–1187 (2002).
Newman, M. E. J. The structure and function of complex networks. SIAM Rev. 45, 167–256 (2003).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D. U. Complex networks: Structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Lieberman, E., Hauert, C. & Nowak, M. A. Evolutionary dynamics on graphs. Nature 433, 312–316 (2005).
Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006).
Perc, M. & Szolnoki, A. Coevolutionary games - A mini review. BioSystems 99, 109–125 (2010).
Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M. & Moreno, Y. Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10, 20120997 (2013).
Szabó, G. & Fáth, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Axelrod, R. & Hamilton, W. D. The Evolution of Cooperation. Science 211, 1390–1396 (1981).
Axelrod, R. More Effective Choices in the Prisoner's Dilemma. J. Conflict Resolut. 24, 379–403 (1980).
Hammerstein, P. The strategy of affect. Genetic and Cultural Evolution of Cooperation. (ed. Hammerstein, P.) 16–16 (MIT, Cambridge, MA 2003).
Axelrod, R. & Hamilton, W. D. The Evolution of Cooperation. Science (London) 211, 1390–1396 (1981).
Turner, P. E. & Chao, L. Prisoner's dilemma in an RNA virus. Nature (London) 398, 441–443 (1999).
Gracia-Lázaro, C., Ferrer, A., Ruiza, G., Tarancón, A., Cuesta, J. A., Sánchez, A. & Moreno, Y. Heterogeneous networks do not promote cooperation when humans play a Prisoner's Dilemma. Proc. Natl. Acad. Sci. USA 109, 12922–12926 (2012).
Semmann, D. Conditional cooperation can hinder network reciprocity. Proc. Natl. Acad. Sci. USA 109, 12846–12847 (2012).
Hauert, C. & Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428, 643–646 (2004).
Doebeli, M. & Hauert, C. Models of cooperation based on the Prisoners Dilemma and the Snowdrift game. Ecol. Lett. 8, 748–766 (2005).
Nowak, M. A. & May, R. M. Evolutionary game and spatial chaos. Nature 359, 826–829 (1992).
Santos, F. C. & Pacheco, J. M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95, 098104 (2005).
Góez-Gardeñs, J., Campillo, M., Floría, L. M. & Moreno, Y. Dynamical organization of cooperation in complex topologies. Phys. Rev. Lett. 98, 108103 (2007).
Taylor, P. D. & Jonker, L. Evolutionarily stable strategies and game dynamics. Math Biosci. 40, 145–156 (1978).
Schuster, P. & Sigmund, K. Replicator dynamics. J. Theor. Biology 100, 533–538 (1983).
Hofbauer, C., Holmes, M. & Michael, D. Evolutionary Games and Population Dynamics: Maintenance of Cooperation in Public Goods Games. Proc. Biol. Sci. 273, 2565–2570 (2006).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature (London) 393, 440–442 (1998).
Barabási, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Schlag, K. H. Why Imitate and If So, How? A Boundedly Rational Approach to Multi-armed Bandits. J. Econ. Theory 78, 130–156 (1998).
Santos, F. C., Pacheco, J. M. & Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 103, 3490–3494 (2006).
Santos, F. C. & Pacheco, J. M. A new route to the evolution of cooperation. J. Evol. Biol. 19, 726–733 (2006).
Santos, F. C., Rodrigues, J. F. & Pacheco, J. M. Epidemic spreading and cooperation dynamics on homogeneous small-world networks. Phys. Rev. E 72, 056128 (2005).
Szolnoki, A. & Szabó, G. Cooperation enhanced by inhomogeneous activity of teaching for evolutionary prisoner's dilemma games. Europhys. Lett. 77, 30004 (2007).
Zhang, Y., Aziz-Alaoui, M. A., Bertelle, C., Zhou, S. & Wang, W. Fence-sitters protect cooperation in complex networks. Phys. Rev. E 88, 032127 (2013).
Szolnoki, A., Perc, M. & Danku, Z. Towards effective payoffs in the prisoner's dilemma game on scale-free networks. Physica A 387, 2075–2082 (2007).
Pinheiro, F. L., Santos, F. C. & Pacheco, J. M. How selection pressure changes the nature of social dilemmas in structured populations. New J. Phys. 14, 073035 (2012).
Zhang, Y., Aziz-Alaoui, M. A., Bertelle, C., Zhou, S. & Wang, W. Emergence of Cooperation in Non-scale-free Networks. J. Phys. A: Math. Theor. 47, 225003 (2014).
Acknowledgements
Y.Z., M.A.A. and C.B. are supported by the region Haute Normandie and the ERDF RISC. J.G. is supported by the National Natural Science Foundation of China, grant Nos. 61173118, 61373036.
Author information
Authors and Affiliations
Contributions
Y.Z., M.A.A. and C.B. designed the experiments together. Y.Z. implement the experiments and prepared all the figures. All authors wrote the main manuscript text together. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Zhang, Y., Aziz-Alaoui, M., Bertelle, C. et al. Local Nash Equilibrium in Social Networks. Sci Rep 4, 6224 (2014). https://doi.org/10.1038/srep06224
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06224
This article is cited by
-
Divide-and-conquer Tournament on Social Networks
Scientific Reports (2017)
-
Emergence of scale-free characteristics in socio-ecological systems with bounded rationality
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.