Abstract
The practical untenability of the quasi-static assumption makes any realistic engine intrinsically irreversible and its operating time finite, thus implying friction effects at short cycle times. An important technological goal is thus the design of maximally efficient engines working at the maximum possible power. We show that, by utilising shortcuts to adiabaticity in a quantum engine cycle, one can engineer a thermodynamic cycle working at finite power and zero friction. Our findings are illustrated using a harmonic oscillator undergoing a quantum Otto cycle.
Similar content being viewed by others
Introduction
THermodynamics is the study of heat and its interconversion to mechanical work. It successfully describes the “equilibrium” properties of macroscopic systems ranging from refrigerators to black holes1. The revolution potentially embodied by the implementation of quantum technologies is motivating the consideration of quantum devices going all the way down to the micro- and nano-scale2. This has forced us to revise our interpretation of thermodynamics to include ab initio both quantum and thermal fluctuations. The former, indeed, become quite prominent at such scales. In fact, far from equilibrium, quantum fluctuations become dominant and cannot be neglected. In turn, thermodynamic quantities such as work and heat become inherently stochastic and should be reformulated accordingly.
Recently discovered work fluctuation theorems (FTs) and the corresponding framework, which is known to hold both in quantum and classical systems, are extremely useful for the task of setting up a quantum apparatus for thermodynamics3,4,5,6,7. FTs set fundamental constraints on the energy fluctuations of a general thermodynamic system and embody useful tools to understand the thermodynamic implications of finite-time transformations8,9. Whether or not FTs can help us shedding light on the limitations or possible advantages of a quantum device operating in finite-time is a very important point to address, that goes beyond the scopes of this paper. However, it is sensible to expect that a convenient platform for the provision of quantitative answers in this sense could come from the study of quantum engines, for which the thermodynamic laws must be recast appropriately10,11,12,13. In fact, although the working principles of a reversible engine might well be quantum mechanical, its efficiency would always be limited by the second law, thus making the quantum version of cycles similar to their classical counterparts.
The assumed reversibility (quasi-stationarity) of an engine cycle, which implies an infinitely long cycle-time, determines its inevitable zero-power nature. This clearly crashes with the reality of any practical machine, either quantum or classical. However, the finite-time operation of a machine working in finite-time exposes it to the effects of friction-induced losses. The key engineering goal in this context is thus to find the maximum efficiency allowed at the maximum possible power15,16. Noticeably, in Ref. 17 an ultra-fast cycle has been discussed that nevertheless attains Carnot efficiency.
Classical approaches to the maximization of the power output of thermal engines have been proposed and developed in the past18,19. While Ref. 14 proposes the use of systematic noise to suppress friction in the expansion and compression stages of a quantum Otto cycle, here we devise an innovative way to run a finite-time, finite-power quantum cycle based on the use of quantum shortcuts to adiabaticity20,21,22,23,24. Such techniques have been employed to show that the Hamiltonian of a quantum system can be manipulated in a way to mimic an adiabatic process via a non-adiabatic shortcut20,21,22,23,24. In this context, the term “adiabatic” should be interpreted as “slow” and will be used, unless the context is evidently different (such as in the description of the cycle), as synonymous of “quasi-static”. A few experiments have demonstrated several of such proposals25,26,27. In this paper we show that such Hamiltonian-engineering techniques allow us to drive the expansion and compression stages of a cycle, which are prone to frictional effects, virtually without any loss affecting the performance of a quantum engine within the finite-time of its cycle. Inspired by a recent ion-trap proposal13, we will provide an example of a finite-time, fully frictionless quantum Otto cycle where the working medium is a quantum harmonic oscillator. Remarkable examples of recent works along the lines of our investigation have been reported recently28,29, although they both address classical analogs of quantum shortcuts to adiabaticity with Deng et al. studying the performance of an Otto cycle from such perspective29.
Results
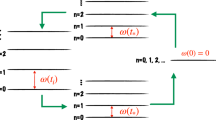
Quantum Otto Cycle. In an Otto engine, a working medium (coupled alternatively to two baths at different temperatures Ti, i = 1, 2) undergoes a four-stroke cycle. In its quantum version, the state of the working medium is described by a density operator ρ(λ(t)) that is changed by the Hamiltonian  . Here, λ(t) is a work parameter, typical of the specific setting used to implement
. Here, λ(t) is a work parameter, typical of the specific setting used to implement  , whose value determines the equilibrium configuration of the system. As illustrated in Fig. 1, the cycle steps are as follows:
, whose value determines the equilibrium configuration of the system. As illustrated in Fig. 1, the cycle steps are as follows:
-
1
An adiabatic expansion performed by the change λ0 ≡ λ(0) → λ1 ≡ λ(τ1), where τ1 is the time at which this step ends. As a result of this transformation, work is extracted from the medium due to the change in its internal energy.
-
2
A cold isochore where heat is transferred from the working medium to the cold bath. This is associated with a heat flow from the medium to the cold reservoir.
-
3
An adiabatic compression performed by the reverse change of the work parameter λ1 → λ0 and during which work is done on the medium.
-
4
A hot isochore during which heat is taken from the hot reservoir by the working medium.
Pressure-volume diagram of a (quantum) Otto cycle.
The numbers relate the processes to the description of each step given in the main text. We identify the steps where heat enters (exits) the working medium and those where work is performed by (done onto) it as a result of a corresponding change in the work parameter λ (t).
If the engine is run in a finite-time, i.e. we abandon the usual quasi-static assumption, friction is generated along the expansion and compression steps. We will elucidate the nature of this friction later on. In addition, one may (realistically) assume imperfect heat conduction during the isochores. Under such conditions, the work W done by/on the engine and the heat Q exchanged by the medium with the baths, become stochastic quantities. The efficiency of the engine is then defined as the ratio between the average total work per cycle and the average heat received from the hot bath, that is

where 〈K〉j (for K = Q, W) is evaluated during step j = 1, …, 4. The power of the engine is then

where τj is the time needed for step j. Here we consider the case where friction only occurs along the adiabatic transformations and neglect fluctuations in the heat flow. On the other hand, we should not forget about the thermalisation process inherent in the isochores, which are associated with the production of entropy. We thus assume to have identified a regime such that the entropy produced by such thermalisation steps is negligible and associated with finite values of τ2,4 (see Supplementary Information for the determination of such a working point and an estimate of both the order of magnitude of such time intervals and of the corresponding production of entropy). Needless to say, the entropy produced during the isochores is the same regardless of the way we perform the adiabats. Moreover, as we will describe in the second part of this paper, the strategy based on shortcuts to adiabaticity that we propose makes 〈W〉i independent of τi. In these conditions, the maximisation of Eq. (2) is achieved by minimizing τ1,3. We now describe our protocol to reduce the time needed for the adiabats and keep the associated friction at bay.
Finite-time thermodynamics. Before we quantify the efficiency of the engine, we need to define the probability distribution of work of which 〈W〉 is the first moment. We consider a Hamiltonian  applied to a system prepared into the Gibbs state
applied to a system prepared into the Gibbs state  . with inverse temperature β and λ(t ≤ 0) = λ0. Here,
. with inverse temperature β and λ(t ≤ 0) = λ0. Here,  is the partition function. At t = 0, the system-reservoir coupling is removed and λ is changed from its initial value λ0 to λ1 at t = τ. Such process could be the expansion/compression step of the Otto cycle, represented by a change of λ in
is the partition function. At t = 0, the system-reservoir coupling is removed and λ is changed from its initial value λ0 to λ1 at t = τ. Such process could be the expansion/compression step of the Otto cycle, represented by a change of λ in  , where |n(λ)〉 is the nth eigenstate with eigenvalue εn(λ). In this context, work should be reformulated in a way to account for both the statistics of the initial state of the system and the non-deterministic nature of quantum measurements30. Under the assumption
, where |n(λ)〉 is the nth eigenstate with eigenvalue εn(λ). In this context, work should be reformulated in a way to account for both the statistics of the initial state of the system and the non-deterministic nature of quantum measurements30. Under the assumption  , the corresponding work distribution P(W;t) reads
, the corresponding work distribution P(W;t) reads

Here we use the notation shortcut |n(t)〉 = |n(λ(t))〉 and call  the probability that, under the action of the evolution operator
the probability that, under the action of the evolution operator  associated with
associated with  , the system goes from the initial state |n(0)〉 to the final one |k(t)〉. Finally,
, the system goes from the initial state |n(0)〉 to the final one |k(t)〉. Finally,  is the occupation probability of the initial state |n(0)〉, which for a Gibbs ensemble reads
is the occupation probability of the initial state |n(0)〉, which for a Gibbs ensemble reads  . For
. For  , this expression needs to be modified31. However, regardless of the value of such commutator, the first two moments of the work distribution read
, this expression needs to be modified31. However, regardless of the value of such commutator, the first two moments of the work distribution read  .
.
For finite systems, the statistical nature of work requires the second law of thermodynamics to be revised to 〈W〉 ≥ ΔF, with ΔF the change in free energy and the equality holding for a quasi-static isothermal process (the inequality holding strictly for all quasi-static processes performed without the coupling to a thermal reservoir). For non-ideal processes, the deficit between 〈W〉 and ΔF can be accounted for by the introduction of the average irreversible work 〈Wirr〉 as 〈W〉 = 〈Wirr〉 + ΔF. The behavior of 〈W〉 will be later compared with the average work 〈Wad〉 performed onto (or made by) the system in an adiabatic process. For such quantity, in the absence of a heat bath, we have 〈Wad〉 > ΔF. For a closed quantum system, the incoming heat flow is null and the irreversible entropy is ΔSirr = β(〈W〉 − ΔF) = β〈Wirr〉, which can be recast as  32 with S(ρA||ρB) = Tr(ρAlnρA − ρAlnρB) the relative entropy between two density matrices ρA and ρB33, ρt the time-evoluted state and
32 with S(ρA||ρB) = Tr(ρAlnρA − ρAlnρB) the relative entropy between two density matrices ρA and ρB33, ρt the time-evoluted state and  the corresponding equilibrium state at the temperature 1/β. Here, 〈Wirr〉 quantifies the degree of friction caused by the finite-time protocol on the expansion or compression stage of the engine cycle. When a bath is reconnected, such friction results in dissipation and hence the decrease in the overall efficiency of the motor. For the point of demonstration we allow only this form of irreversibility in our cycle, although in principle the same analysis can be done for fluctuating heat flows34,35.
the corresponding equilibrium state at the temperature 1/β. Here, 〈Wirr〉 quantifies the degree of friction caused by the finite-time protocol on the expansion or compression stage of the engine cycle. When a bath is reconnected, such friction results in dissipation and hence the decrease in the overall efficiency of the motor. For the point of demonstration we allow only this form of irreversibility in our cycle, although in principle the same analysis can be done for fluctuating heat flows34,35.
Friction-free finite-time engine. Recently, substantial work has been devoted to the design of super-adiabatic protocols, i.e. shortcuts to states which are usually reached by slow adiabatic processes20,21,22,24. A typical approach for shortcuts to adiabaticity is to use ad hoc dynamical invariants to engineer a Hamiltonian model that connects a specific eigenstate of a model from an initial to a final configuration determined by a dynamical process. Here we will rely on an approach based on engineered non-adiabatic dynamics achieved using self-similar transformations23,36.
Let us consider a quantum harmonic oscillator with time-dependent frequency ω(t) as the working medium of the engine cycle23. The Hamiltonian model that we consider is thus  , where
, where  and
and  are the position and momentum operators of an oscillator of mass m. Inspired by the scheme in Ref. 13, we will use the tuneable harmonic frequency to implement the compression and expansion steps of the Otto cycle. In line with such proposal, the frequency of the harmonic trap embodies the volume of the chamber into which the working medium is placed, while the corresponding pressure is defined in terms of the change of energy per unit frequency.
are the position and momentum operators of an oscillator of mass m. Inspired by the scheme in Ref. 13, we will use the tuneable harmonic frequency to implement the compression and expansion steps of the Otto cycle. In line with such proposal, the frequency of the harmonic trap embodies the volume of the chamber into which the working medium is placed, while the corresponding pressure is defined in terms of the change of energy per unit frequency.
Clearly, in the compression or expansion stage of the Otto cycle, the frequency of the trap will have to be varied, so that ω(t) takes here the role of a work parameter. We now suppose to subject the working medium to a change in the work parameter occurring in a time τ and corresponding to one of the friction-prone steps of the Otto cycle. Our goal is to design an appropriate shortcut to adiabaticity to arrange for a fast, frictionless evolution between the configurations of the working medium at t = 0 and that at t = τ. In order to do this, we remind that the wavefunction ϕn(x, t = 0) = 〈x|n(0)〉 of an initial eigenstate |n(0)〉 of  is known to follow the self-similar evolution23
is known to follow the self-similar evolution23

where  , εn(0) is the energy of the eigenstate being considered at t = 0 and the scaling factor b is the solution of the Ermakov equation
, εn(0) is the energy of the eigenstate being considered at t = 0 and the scaling factor b is the solution of the Ermakov equation

with the initial conditions b(0) = 1 and  . Needless to say, while the physically relevant parameter is the time-dependent frequency ω(t), the determination of the exact scaling parameter b(t) is key for the engineering of the correct shortcut to adiabaticity. This is found by inverting the Ermakov equation and complementing the previous set of boundary conditions with
. Needless to say, while the physically relevant parameter is the time-dependent frequency ω(t), the determination of the exact scaling parameter b(t) is key for the engineering of the correct shortcut to adiabaticity. This is found by inverting the Ermakov equation and complementing the previous set of boundary conditions with  and
and  with ω0 = ω(0) and ωf = ω(τ). An instance of the solution to this problem can be found in the Methods, where we give the explicit form of b(t) such that the finite-time dynamics taking the initial state ϕn(x, t = 0) = 〈x|n(0)〉 to the final one
with ω0 = ω(0) and ωf = ω(τ). An instance of the solution to this problem can be found in the Methods, where we give the explicit form of b(t) such that the finite-time dynamics taking the initial state ϕn(x, t = 0) = 〈x|n(0)〉 to the final one  mimics the wanted adiabatic evolution (albeit for any t ∈ (0, τ), ϕn(x, t) is in general different from the eigenstate |n(t)〉 of
mimics the wanted adiabatic evolution (albeit for any t ∈ (0, τ), ϕn(x, t) is in general different from the eigenstate |n(t)〉 of  ). The choice of a harmonic oscillator is not a unique example as analogous self-similar dynamics can be induced in a large family of many-body systems36 and other trapping potentials, such as a quantum piston37. The resilience of the shortcuts to adiabaticity approach to imperfections in the engineering of the exact functional form of the time-dependent protocol embodied by ω(t) is an important point to address. Overall, shortcuts to adiabaticity are known to be robust against perturbations, as discussed in Ref. 23 for the case of an approximately harmonic trap and in Ref. 36 for other trapping potentials.
). The choice of a harmonic oscillator is not a unique example as analogous self-similar dynamics can be induced in a large family of many-body systems36 and other trapping potentials, such as a quantum piston37. The resilience of the shortcuts to adiabaticity approach to imperfections in the engineering of the exact functional form of the time-dependent protocol embodied by ω(t) is an important point to address. Overall, shortcuts to adiabaticity are known to be robust against perturbations, as discussed in Ref. 23 for the case of an approximately harmonic trap and in Ref. 36 for other trapping potentials.
Let us consider the fluctuations induced in the expansion and compression stages of the Otto cycle when the above shortcut to adiabaticity is implemented. Let us consider a driving Hamiltonian with instantaneous eigenstates |n(t)〉 and eigenvalues εn(t). In the adiabatic limit, the corresponding transition probabilities  tend to |〈n(t)|k(t)〉|2 = δk,n(t) for all t ∈ [0, τ]. The average work is then
tend to |〈n(t)|k(t)〉|2 = δk,n(t) for all t ∈ [0, τ]. The average work is then  . On the other hand, in a shortcut to adiabaticity, only the weaker condition
. On the other hand, in a shortcut to adiabaticity, only the weaker condition  holds. For the time-dependent harmonic oscillator, it follows that
holds. For the time-dependent harmonic oscillator, it follows that

In the adiabatic limit  and
and  .
.
Fig. 2(a) shows 〈W〉 along a shortcut to an adiabatic expansion in comparison with the corresponding adiabatic process 〈Wad(t)〉 (the behavior observed during a shortcut to a compression is mirrored in time). We stress that 〈W〉 is the work done on either adiabat until the reconnection with the bath, i.e. just prior to the isochoric heating/cooling stage. Fig. 2(b) displays the standard deviation ΔW = [〈W2〉 − 〈W〉2]1/2, which provides a further characterisation of the work fluctuations along the shortcut through the width of P(W;t). Interestingly, upon completion of the stroke, the non-equilibrium deviation of both the average work and the standard deviation from the adiabatic trajectory disappear.
Work fluctuations along a shortcuts to an adiabaticity expansion.
(a) Average work; (b) Standard deviation of the work; (c) Non-equilibrium deviations from the adiabatic average mean work; (d) We show  (
( and
and  ) and
) and  (
( and
and  ) [cf. Eq. (7)] for the same processes shown in the other panels. All quantities are plotted in units of ħω0(β = 1).
) [cf. Eq. (7)] for the same processes shown in the other panels. All quantities are plotted in units of ħω0(β = 1).
We shall now analyse the non-equilibrium deviation δW = 〈W〉 − 〈Wad(t)〉 with respect to 〈Wad(t)〉. This is equivalent to the deviation of the mean energy of the motor along the super-adiabats from its (instantaneous) adiabatic expression. For a reversible isothermal process 〈Wad〉 = ΔF and δW = 〈Wirr〉. Differently, for the adiabatic dynamics of stages 1 and 3 of the Otto cycle, conservation of the population in |n(t)〉 is satisfied provided that βt = βεn(0)/εn(t), as it is the case for a large-class of self-similar processes, as discussed in Refs. 23,36,37 and remarked in the Supplementary Information. Here, βt is introduced by noticing that the physical adiabatic state at time t is characterised by the occupation probabilities  . Therefore, the reference state
. Therefore, the reference state  is not the physical instantaneous equilibrium state
is not the physical instantaneous equilibrium state  resulting from the adiabatic dynamics and we find
resulting from the adiabatic dynamics and we find

Therefore, in general δW ≠ 0. However, one can check that at the end of the process we have  , which implies δW = 0 and thus the frictionless nature of the process [cf. Fig. 2(c)]. The time-evolution of the different contribution to δW, i.e.
, which implies δW = 0 and thus the frictionless nature of the process [cf. Fig. 2(c)]. The time-evolution of the different contribution to δW, i.e. and
and  , are displayed in Fig. 2(d). This result is remarkable in the context of the quantum Otto cycle: If the baths are reconnected at time τ after both the compression and expansion stages, then the efficiency of an ideal reversible engine can be reached in finite-time, thus implementing a frictionless finite-time cycle. As friction is the only source of irreversibility in our scheme, the super-adiabatic engine reaches the maximum efficiency of an ideal quasi-static engine in a finite-time only.
, are displayed in Fig. 2(d). This result is remarkable in the context of the quantum Otto cycle: If the baths are reconnected at time τ after both the compression and expansion stages, then the efficiency of an ideal reversible engine can be reached in finite-time, thus implementing a frictionless finite-time cycle. As friction is the only source of irreversibility in our scheme, the super-adiabatic engine reaches the maximum efficiency of an ideal quasi-static engine in a finite-time only.
Let us address a final point: The efficiency in Eq. (1) diminishes with the breakdown of adiabaticity13. In contrast, our super-adiabatic engine achieves the maximum possible value  . Clearly, if unlimited resources are available, there is no fundamental lower-bound on the running time of the adiabats. However, we take a pragmatic approach and quantify the energy cost associated with the implementation of our super-adiabatic engine, which would provide a significant cost function for such part of the cycle. We have thus considered the time-averaged dissipated work
. Clearly, if unlimited resources are available, there is no fundamental lower-bound on the running time of the adiabats. However, we take a pragmatic approach and quantify the energy cost associated with the implementation of our super-adiabatic engine, which would provide a significant cost function for such part of the cycle. We have thus considered the time-averaged dissipated work  , ensuring ω2(t) > 0 for t ∈ [0, τ]. The cut-off time τc was taken as the maximum running time along the shortcut of each super-adiabat before the trap is inverted (cf. Methods section). When this occurs, the adiabatic eigen-energies are not well defined and our formalism breaks down. For the shortcut to adiabaticity discussed here, such inversion occurs when the expansion time is smaller than the inverse of the initial frequency of the trap36. The exact value of such critical running time, which depends on the expansion factor and can be found numerically, is different for expansion and compression stages, being larger in the former case. While the steps necessary for the calculation of 〈δW〉 are reported in the Supplementary Information, here is enough to mention that the cost of running the super-adiabatic engine exhibits a 〈δW〉 ~ 1/τ behavior for a wide range of parameters, as shown in Fig. 3. This demonstrates the existence of a trade-off between the running time of the super-adiabatic transformations and the corresponding amount of time-averaged dissipated work, in line with the analogous compromise between the irreversible entropy produced along the isochores and the running time of the transformations. An upper bound for the power of an engine run can be calculated using the fundamental limitations set by quantum speed limit. The key steps of such calculations are discussed in the Supplementary Information.
, ensuring ω2(t) > 0 for t ∈ [0, τ]. The cut-off time τc was taken as the maximum running time along the shortcut of each super-adiabat before the trap is inverted (cf. Methods section). When this occurs, the adiabatic eigen-energies are not well defined and our formalism breaks down. For the shortcut to adiabaticity discussed here, such inversion occurs when the expansion time is smaller than the inverse of the initial frequency of the trap36. The exact value of such critical running time, which depends on the expansion factor and can be found numerically, is different for expansion and compression stages, being larger in the former case. While the steps necessary for the calculation of 〈δW〉 are reported in the Supplementary Information, here is enough to mention that the cost of running the super-adiabatic engine exhibits a 〈δW〉 ~ 1/τ behavior for a wide range of parameters, as shown in Fig. 3. This demonstrates the existence of a trade-off between the running time of the super-adiabatic transformations and the corresponding amount of time-averaged dissipated work, in line with the analogous compromise between the irreversible entropy produced along the isochores and the running time of the transformations. An upper bound for the power of an engine run can be calculated using the fundamental limitations set by quantum speed limit. The key steps of such calculations are discussed in the Supplementary Information.
Quantum cost of running the super-adiabatic expansion stage of the quantum Otto cycle.
We plot the time-averaged deviation 〈δW〉 of the mean energy of the system from the adiabatic eigen-energies for three values of β and  . In all cases there is an effective power-law scaling of the form 〈δW〉 ~ 1/τ. The cut-off time is such that the confining potential remains a trap along the process, without the need for transiently inverting it to achieved the required speed up.
. In all cases there is an effective power-law scaling of the form 〈δW〉 ~ 1/τ. The cut-off time is such that the confining potential remains a trap along the process, without the need for transiently inverting it to achieved the required speed up.
Discussion
We have demonstrated the possibility to perform a fully frictionless quantum cycle in a finite-time. Our proposal exploits the idea of shortcuts to adiabaticity, which allowed us to bypass the effects of friction on the compression and expansion stages in an important cycle such as Otto's. Our study embodies one example of the potential brought about by the combination of shortcuts to adiabaticity and the framework for out-of-equilibrium dynamics of a quantum system. The possibility to achieve maximum efficiency of a quantum engine at finite time with virtually no friction is tantalizing in the perspective of designing micro- and nano-scale motors operating at the verge of quantum mechanics.
Methods
Driving protocol of the super-adiabats
Here we illustrate the formal procedure for the determination of the scaling factor b(t) used in the super-adiabatic steps of our proposal. The simplest interpolation of the actual solution of the Ermakov equation in the main body of the paper with the boundary conditions stated in the main text is found to be the polynomial

with s = t/τ. This solution guarantees that, in the adiabatic limit, b·(t) → 0 and b(t) → bad, while more generally the eigenstates of the initial oscillator will evolve according to the scaling law in Eq. (4). The modulation of ω(t) is the responsible for the speed-up of the transformations performed along the super-adiabats. In turn, the implementation of such modulation is the price to pay for the achievement of such advantage. The explicit form ω(t) can be extracted from the Ermakov equation,  , using Eq. (8) for b(t), see Fig. (4). For sufficiently small values of ω0τ, ω(t) can become purely imaginary (requiring the inversion of the trap into an expelling barrier). The condition ω2(t) > 0 provides the cut-off time τc used in Fig. 3.
, using Eq. (8) for b(t), see Fig. (4). For sufficiently small values of ω0τ, ω(t) can become purely imaginary (requiring the inversion of the trap into an expelling barrier). The condition ω2(t) > 0 provides the cut-off time τc used in Fig. 3.
References
Goldstein, M. & Gloldstein, F. I. The Refrigerator and the Universe (Harvard Univ. Press, 1993).
Wolf, E. L. & Medikonda, M. Understanding the Nanotechnology Revolution (Wiley-VCH, 2012).
Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 78, 2690 (1997).
Crooks, G. E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 60, 2721 (1999).
Tasaki, H. Jarzynski Relations for Quantum Systems and Some Applications. arXiv.org.:cond-mat/0009244 (2000).
Kurchan, J. A Quantum Fluctuation Theorem. arXiv.org.:cond-mat/0007360v2 (2000).
Mukamel, S. Quantum Extension of the Jarzynski Relation: Analogy with Stochastic Dephasing. Phys. Rev. Lett. 90, 170604 (2003).
Jarzynski, C. Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 3, 329 (2011).
Campisi, M., Hänggi, P. & Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 83, 771 (2011).
Gemmer, J., Michel, M. & Mahler, G. Quantum Thermodynamics (Springer, 2004).
Scovil, H. E. D. & Schulz-DuBois, E. O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 2, 262 (1959).
Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A 12, L103 (1979).
Abah, O. et al. Single-Ion Heat Engine at Maximum Power. Phys. Rev. Lett. 109, 203006 (2012).
Feldman, T. & Kosloff, R. Quantum lubrication: Suppression of friction in a first-principles four-stroke heat engine. Phys. Rev. E 73, 025107(R) (2006).
Curzon, F. & Ahlborn, B. Endoreversible thermodynamics. Am. J. Phys. 43, 22 (1975).
Esposito, M., Kawai, R., Lindenberg, K. & Van den Broeck, C. Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Phys. Rev. Lett. 105, 150603 (2010).
Gelbwaser-Klimovsky, D., Alicki, R. & Kurizki, G. Minimal universal quantum heat machine. Phys. Rev. E 87, 012140 (2013).
Orlov, V. N. & Berry, R. S. Power and efficiency limits for internal combustion engines via methods of finite-time thermodynamics. J. Appl. Phys. 74, 4317 (1993).
Feldmann, T. & Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 61, 4774 (2000).
Demirplak, M. & Rice, S. A. Adiabatic population transfer with control fields. J. Chem. Phys. A 107, 9937 (2003).
Demirplak, M. & Rice, S. A. Assisted adiabatic passage revisited. J. Chem. Phys. B 109, 6838 (2005).
Berry, M. V. Transitionless quantum driving. J. Phys. A: Math. Theor. 42, 365303 (2009).
Chen, X. et al. Fast Optimal Frictionless Atom Cooling in Harmonic Traps: Shortcut to Adiabaticity. Phys. Rev. Lett. 104, 063002 (2010).
Torrontegui, E. et al. Shortcuts to adiabaticity Adv. At. Mol. Opt. Phys. 62, 117 (2013).
Schaff, J.-F., Song, X.-L., Vignolo, P. & Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 82, 033430 (2010).
Schaff, J.-F., Song, X.-L., Capuzzi, P., Vignolo, P. & Labeyrie, G. Shortcut to adiabaticity for an interacting Bose-Einstein condensate. EPL 93, 23001 (2011).
Bason, M. G. et al. High-fidelity quantum driving. Nature Phys. 8, 147 (2012).
Jarzynski, C. Generating shortcuts to adiabaticity in quantum and classical dynamics. Phys. Rev. A 88, 040101(R) (2013).
Deng, J., Wang, Q.-h., Liu, Z., Hänggi, P. & Gong, J. Boosting work characteristics and overall heat-engine performance via shortcuts to adiabaticity: Quantum and classical systems. Phys. Rev. E 88, 062122 (2013).
Talkner, P., Lutz, E. & Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 75, 050102R (2007).
Suomela, S., Solinas, P., Pekola, J. P., Ankerhold, J. & Ala-Nissila, T. arXiv,1404.0610 (2014).
Deffner, S. & Lutz, E. Generalized Clausius Inequality for Nonequilibrium Quantum Processes. Phys. Rev. Lett. 105, 170402 (2010).
Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 74, 197 (2002).
Jarzynski, C. & Wojcik, D. K. Classical and Quantum Fluctuation Theorems for Heat Exchange. Phys. Rev. Lett. 92, 230602 (2004).
Jennings, D. et al. arXiv,1204.3571 (2012).
del Campo, A. Frictionless quantum quenches in ultracold gases: A quantum-dynamical microscope. Phys. Rev. A, 84, 031606(R) (2011).
del Campo, A. & Boshier, M. G. Shortcuts to adiabaticity in a time-dependent box. Sci. Rep. 2, 648 (2012).
Acknowledgements
We are grateful to G. De Chiara, B. Damski, S. Deffner, R. Dorner, R. Fazio, C. Jarzynski, E. Passemar and N. Sinitsyn for discussions and comments on this work. AdC is supported by the U.S. Department of Energy through the LANL/LDRD Program and a LANL J. Robert Oppenheimer fellowship. JG acknowledges funding from IRCSET through a Marie Curie International Mobility fellowship. MP thanks the UK EPSRC for a Career Acceleration Fellowship and a grant under the “New Directions for EPSRC Research Leaders” initiative (EP/G004579/1) the John Templeton Foundation (grant 43467), the EU Collaborative project TherMiQ (Grant Agreement 618074) and the COST Action MP1209.
Author information
Authors and Affiliations
Contributions
A.d.C. and J.G. developed the calculation for the concept proposed by M.P. All authors interpreted the results and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Campo, A., Goold, J. & Paternostro, M. More bang for your buck: Super-adiabatic quantum engines. Sci Rep 4, 6208 (2014). https://doi.org/10.1038/srep06208
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06208
This article is cited by
-
Identifying optimal cycles in quantum thermal machines with reinforcement-learning
npj Quantum Information (2022)
-
Quantum acceleration by an ancillary system in non-Markovian environments
Quantum Information Processing (2021)
-
Construction of a quantum Carnot heat engine cycle
Quantum Information Processing (2020)
-
Quantum Carnot cycle with inner friction
Quantum Information Processing (2020)
-
An interaction-driven many-particle quantum heat engine and its universal behavior
npj Quantum Information (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.