Abstract
The Jackiw-Rebbi model describes a one-dimensional Dirac field coupled to a soliton field and can be equivalently thought of as a model describing a Dirac field with a spatially dependent mass term. Neglecting the dynamics of the soliton field, a kink in the background soliton profile yields a topologically protected zero-energy mode for the field, which in turn leads to charge fractionalisation. We show here that the model, in the first quantised form, can be realised in a driven slow-light setup, where photons mimic the Dirac field and the soliton field can be implemented–and tuned–by adjusting optical parameters such as the atom-photon detuning. Furthermore, we discuss how the existence of the zero-mode and its topological stability can be probed naturally by studying the transmission spectrum. We conclude by analysing the robustness of our approach against possible experimental errors in engineering the Jackiw-Rebbi Hamiltonian in this optical setup.
Similar content being viewed by others
Introduction
Quantum simulators first and foremost offer a promising alternative when analytical and numerical methods fail in analysing models with strong correlations. On the other hand, they can also be used in probing exotic physical phenomena such as those predicted by relativistic theories. To date, a collection of effects in different fields ranging from condensed matter physics to relativistic quantum theories and material science have been simulated1, using different platforms such ion traps2 and cold atoms in optical lattices3.
More recently, the ability to controllably manipulate photons and their interactions with atomic systems resulted in the birth of a new direction in quantum simulations using photons and polaritons to mimic strongly correlated phenomena. Coupled cavity QED arrays (CCAs) were initially considered, where photons trapped in resonators interfaced with two level atoms (real or artificial ones) were shown to be able to reproduce many-body dynamics4,5,6. The so-called photon blockade effect was exploited and polariton Mott transitions and effective spin-models were proposed, introducing what is now known as the Jaynes-Cummings-Hubbard (JCH) model7. Simultaneously and independently, the possibility for strongly correlated polariton dynamics in CCAs with four-level atoms and external fields was proposed8, followed soon after by the JCH's phase diagram9,10 and the Fractional Hall effect11. More recently one dimensional highly nonlinear waveguides with slow-light nonlinearities12,13,14 have been considered where effects characterising Tonks-Girardeau gas, Luttinger liquids physics, or even interacting relativistic theories have been shown to be simulable15,16,17. The possibility to probe out-of-equilibrium phenomena has also been explored in driven setups18,19
Quantum simulation has also shown great development in bringing the exotic physics of single particle relativistic effects into laboratory. These range from numerous theoretical works studying the Dirac equation and emerging effects such as the trembling motion of the electron (Zitterbewegung) or Klein tunneling to experimental implementations of those in different platforms covering all three mentioned above. More specifically in ion technologies the Dirac equation in 1 + 1 dimensions has been realised20,21,22,23 followed by an implementation with photons in waveguide arrays, including the random mass Dirac model24,25,26. Seminal proposals for the realisation in slow-light systems also exist27,28,29,30. Going beyond the Dirac equation, recent works have proposed to simulate the Majorana equation31,32 and neutrino oscillations33 in trapped ions.
The purpose of this article is to propose a quantum simulation of a historically important relativistic model known as the Jackiw-Rebbi (J-R) model34 with slow-light. The model describes a one-dimensional Dirac field coupled to a static background soliton field and can be equivalently thought of as the model describing a massless Dirac particle under a Lorentz scalar potential. The same model has been studied independently by Su, Schrieffer and Heeger (SSH), while studying electron-phonon coupling arising in polyacetylene, in the continuum limit35. The model is well known for predicting charge fractionalisation36, well before fractional quantum Hall effect was discovered and also for the topological nature of its zero-energy solution and can be thought of as a precursor to topological insulators, a topic that is being hotly pursued37,38.
There have been proposals to realise the model and observe charge fractionalisation in an optical lattice setup39,40 and experimental observation of the soliton which follows the model in a fermionic superfluid41. Also, there have been proposals to observe topological bound states analogous to that arising in the model, in quantum walk and graphene setups42,43,44,45. A topological bound state has also been observed in optically-induced dimer lattices46, where the latter is closely related to the SSH model. Here, we follow a different route and propose a photonic implementation of the model in a slow-light polaritonic setup and show that the topological properties can be probed straightforwardly in an optical transmission experiment. We would like to highlight here that the usual experimental difficulties, in realising the photonic nonlinear interaction in slow-light systems for more complex many body simulations, do not exist in this case. Therefore we believe the proposal is a good candidate for directly realising the J-R model and could allow the efficient probing of its topological properties for the first time.
The Jackiw-Rebbi model and the related model studied by Su, Schrieffer and Heeger35 share many features similar to those studied in topological insulators and might indeed be classified as an AIII-type chiral topological Dirac insulator under a suitable regularisation47. Here we describe the Jackiw-Rebbi model and point out the topological properties and similarities to topological insulators. The equation of motion considered by Jackiw and Rebbi reads

where α and β are the Dirac matrices which in this case can be chosen to be proportional to two Pauli matrices. For concreteness, we take them to be α = σz and β = σy. The real scalar field ϕ(z) is assumed to obey the Klein-Gordon equation of the form

The ground state of the scalar field is degenerate at ϕ(z) = ±κ, which implies the existence of a soliton that interpolates between −κ at z = −∞ and κ at z = ∞ and corresponding anti-soliton. The soliton localised at z = 0 is described by

When the Dirac field is coupled to such a soliton, a zero-mode (zero energy state) appears which is localised around the soliton. The unnormalised spinor wave function of this zero-mode reads

where αβχ = −iχ and is shown in Fig. 1 (solid red curve). Note that the dynamics of the scalar field is neglected in the above argument, i.e., the scalar field is treated as a constant background field.
Far away from the kink, the particle and hole bands have an energy gap m, whereas this gap must close at the point ϕs(z) = 0. This resembles the gap closing at the boundary of a topological insulator where the bound surface mode develops. The resulting bound state, the zero-mode, is protected by the topology of the scalar field, whose existence, irrespective of the local profile of the kink, is guaranteed by the so-called index theorem34,48. This phenomenon is similar to the emergence of edge modes in the quantum Hall effect49,50 or topological insulators37,38, where edge modes appear at the boundary of two topologically different domains.
Another interesting aspect of the model (when second quantisation is taken into account) is charge fractionalisation, which we briefly describe before moving on to a proposal for a photonic implementation. The ground state of the Dirac field (the vacuum) in the soliton background may or may not include the zero-mode. Because of the charge conjugation symmetry of the system, the two degenerate ground states must have opposite charges. Moreover, the charge difference between the two must be 1, as there can be only one electron occupying the state. The result is that the filled or unfilled states must have charges 1/2 and −1/2, respectively. This result can be confirmed by constructing the formal charge operator in terms of creation and annihilation operators of the eigenmodes. The vacuum states are the eigenstates of the charge operators which means that the observed fractional charges are sharp and are not just a trivial realisation of a distributed charge.
Results
Slow-light realisation of J-R dynamics
The spinor slow-light setup we employ to realise the J-R model and subsequently observe the zero-mode is depicted in Fig. 2. This setup was first proposed by Ruseckas et al.30, to which we refer the reader for a detailed explanation. The system comprises of a waveguide system coupled to an ensemble of atoms, which could be realised either in a tapered fiber51,52 or a hollow-core waveguide53,54,55,56,57. The atoms are characterised by the three hyperfine ground levels; one populated state |g〉 and two unpopulated states |s1〉 and |s2〉. These ground states are coupled to the two excited states |e1〉 and |e2〉 by the probe and control fields. The counter-propagating probe beams are described by the electric field amplitudes E1 and E2, with the respective central frequencies ω1 and ω2 and drive the transitions |g〉 → |e1〉 and |g〉 → |e2〉. The propagation of the probe beams is controlled by two pairs of counter-propagating control lasers with Rabi frequencies Ωj1 and Ωj2 (with j = 1, 2), driving the transitions from the excited states to the unpopulated states. A slowly varying amplitude  is associated with the electric field strength Ej of the jth probe field:
is associated with the electric field strength Ej of the jth probe field:

with k1 = ω1 and k2 = −ω2, where the speed of light in an empty waveguide is taken to be 1.
(a), Schematic diagram of the optical waveguide system, interfaced with an ensemble of atoms where propagating light fields  and
and  play the role of Dirac spinor components. By adjusting the relevant optical couplings and detunings, the J-R model can be simulated and its topological aspects probed by looking at the transmission spectrum. (b), The level structure of the interfaced atoms.
play the role of Dirac spinor components. By adjusting the relevant optical couplings and detunings, the J-R model can be simulated and its topological aspects probed by looking at the transmission spectrum. (b), The level structure of the interfaced atoms.
The propagation of the slowly varying amplitudes is such that they follow the 1 + 1 dimensional Dirac-like equation

v0 = Ω2/g2n is the group velocity much smaller than 1, where  is the Rabi frequency of the control fields, g is the atom-light coupling strength and n is the atomic density. The complex Rabi frequencies are tuned so that S11 = S22 = 0 and S12 = S21 = S where
is the Rabi frequency of the control fields, g is the atom-light coupling strength and n is the atomic density. The complex Rabi frequencies are tuned so that S11 = S22 = 0 and S12 = S21 = S where  .
.  is a column vector of two slowly-varying field components
is a column vector of two slowly-varying field components  and
and  , i.e.,
, i.e.,  and δ is the two-photon detuning. In the limit S = π/2, the above equation reduces to the Dirac equation in 1 + 1 dimension
and δ is the two-photon detuning. In the limit S = π/2, the above equation reduces to the Dirac equation in 1 + 1 dimension

which is equal to the Dirac equation introduced in the previous section with the identifications c = v0 and mc2/κ = δ.
The connection with the J-R model is obvious once we let δ be spatially varying as δ(z) = δ0 tanh(λz). This is possible, for example, by introducing additional lasers and states to induce AC Stark shift in the metastable states |s1〉 and |s2〉. Spatial variations in the lasers can then induce an arbitrary mass profile, including the desired soliton profile. A similar model has been studied in Ref. 29 with a slightly different atomic level scheme and the existence of zero-mode has been briefly commented on, although no connection with the J-R model has been made nor the topological nature of the zero-mode mentioned. By making the connection, it is easily seen that there is interesting physics to be explored in the slow-light system, namely the topologically protected zero-mode. In the following, we discuss how the zero-mode and its topological stability can be observed experimentally.
Probing the zero-mode and its topological stability
Broadly speaking, there are two possible ways to observe the zero-mode in this optical setup. The first is an adiabatic method, where a photonic wave packet is adiabatically loaded to prepare an initial state that resembles the zero-mode whose evolution is then observed. In this method, the initial state is prepared by capturing a pulse in the medium via the usual electromagnetically induced transparency (EIT) technique, i.e., by slowly turning off the forward-traveling control fields which are initially on12. Then, all the control fields are slowly turned on again, including the coupling fields Ω12 and Ω21. At this point, the pulses are trapped as stationary light and go through the effective evolution governed by the Dirac equation. The dynamics of the spinor fields then differ significantly, depending on the initial condition of the wave packets as shown in Fig. 3, where we have solved the Dirac equation with the initial gaussian wave packet  with σ = 1.2 and χ = (1, 1)T to mimic the zero-mode spinor. In the case of the J-R model, i.e., under the soliton mass profile, the wave packet is trapped around the kink (upper row of Fig. 3), while under the normal case of constant mass, the wave packet spreads out (bottom row of Fig. 3).
with σ = 1.2 and χ = (1, 1)T to mimic the zero-mode spinor. In the case of the J-R model, i.e., under the soliton mass profile, the wave packet is trapped around the kink (upper row of Fig. 3), while under the normal case of constant mass, the wave packet spreads out (bottom row of Fig. 3).
Dynamics of an optical gaussian wave packet mimicking the zero-mode wave function (4) in the J-R model (top row), compared with its evolution under the Dirac equation (bottom row).
The overlap between the zero-mode and the gaussian wave functions is ≈ 0.997. In the first case the coupling to the background soliton forces the initial wave packet to be trapped, while the second case shows the expected wave function spreading for a Dirac particle of mass δ0.  and
and  corresponds to the top and bottom parts of the spinor, respectively.
corresponds to the top and bottom parts of the spinor, respectively.
The second method, better suited for this particular experimental realisation, is to look at the transmission and reflection of an incident probe field  . Similar studies have been carried out quite recently, using transmission to probe strongly interacting effects in similar polaritonic systems58,59,60. Consider a monochromatic probe field
. Similar studies have been carried out quite recently, using transmission to probe strongly interacting effects in similar polaritonic systems58,59,60. Consider a monochromatic probe field  impinging from the left, while
impinging from the left, while  where L is the length of the system. One can study the transmission and reflection spectrum of this field where the transmitted field will come out to the right of the waveguide as
where L is the length of the system. One can study the transmission and reflection spectrum of this field where the transmitted field will come out to the right of the waveguide as  , whereas the reflected part is
, whereas the reflected part is  as shown in Fig. 2a. The constant mass case can be solved analytically30 and shows the behaviour depicted in Fig. 4a. There is a finite window of perfect reflection due to the well known band gap proportional to the mass energy. Upon introducing the spatially dependent mass term discussed earlier, i.e. tanh(λz), transmission reappears at the center of the bandgap as shown in Fig. 4b, which can be attributed to the presence of the zero-mode. Here and below, we follow Ref. 30 and assume that the length of the atomic cloud interacting with the propagating light is L = 300 μm and the latter's group velocity v0 = 17 m/s. For these values, the maximum two photon detuning δ0 = 0.25v0/L lies well within the EIT transparency window.
as shown in Fig. 2a. The constant mass case can be solved analytically30 and shows the behaviour depicted in Fig. 4a. There is a finite window of perfect reflection due to the well known band gap proportional to the mass energy. Upon introducing the spatially dependent mass term discussed earlier, i.e. tanh(λz), transmission reappears at the center of the bandgap as shown in Fig. 4b, which can be attributed to the presence of the zero-mode. Here and below, we follow Ref. 30 and assume that the length of the atomic cloud interacting with the propagating light is L = 300 μm and the latter's group velocity v0 = 17 m/s. For these values, the maximum two photon detuning δ0 = 0.25v0/L lies well within the EIT transparency window.
The reflection |R|2 (black) and transmission |T|2 (red) curves for the effective Dirac particle (a), without the soliton background and (b), with a soliton field whose profile is 0.25 tanh(0.02z).
(a) shows the Dirac mass bandgap whereas (b) shows near-unity transmission near the zero-energy due to the bound zero-mode.
Using this second method, the topological nature of the zero-mode can be readily probed by looking at the transmission spectrum while perturbing the mass profile. The latter can be done by tuning the two photon detunings using standard optical methods, like AC stark shifting used in slow-light experiments12,13. Changing the hyperbolic tangent function to the sine function while preserving the topology of the profile, i.e., the mass term takes the value of −δ0 and +δ0 at z = −L/2 and z = L/2 respectively and crosses 0 only once at the origin, has little effect on the transmission at the center of the bandgap as shown in Fig. 5a. The extreme limit where the ‘kink’ has been straightened out such that the background profile is linear is also shown in Fig. 5b. The zero-mode persists in this extreme case, clearly demonstrating the topologically protected robustness. The zero-mode is also protected from random fluctuations in the mass profile as shown in Fig. 5c and d, where we have assumed random fluctuations within 20% and 50% of δ(z), i.e.,  where
where  is a uniform random with the resolution of 0.1 μm. Such topological protection holds as long as the fluctuations do not destroy the topology (two distinct values at the infinity and one zero-crossing only) of the soliton background. Unusually large fluctuations that changes the topology could destroy the zero-mode, but are unlikely in experimental implementations.
is a uniform random with the resolution of 0.1 μm. Such topological protection holds as long as the fluctuations do not destroy the topology (two distinct values at the infinity and one zero-crossing only) of the soliton background. Unusually large fluctuations that changes the topology could destroy the zero-mode, but are unlikely in experimental implementations.
(a), (b), Stability of the zero-mode under changes in the background profile and (c), (d), random fluctuations in the soliton profile, implemented via the two photon detunings. (a), Background profile changed to the sine function δ(z) = 0.25 sin(0.01z). (b), Soliton profile changed to the linear function going from −0.25 to 0.25. In both cases, the response of the system around resonance remains similar to Fig. 4b. (c), (d), Added random fluctuations where the maximum value of the random fluctuation  is 0.2 and 0.5. We see that the zero-mode persists in spite of the relatively large values of fluctuation although the maximum possible transmission is gradually reduced from roughly 95% to 85%.
is 0.2 and 0.5. We see that the zero-mode persists in spite of the relatively large values of fluctuation although the maximum possible transmission is gradually reduced from roughly 95% to 85%.
Experimentally, it might be difficult to set the phases of the control fields exactly to the required value of the mixing angle S = π/2 in Eq. (6), in which case the resulting equation deviates from the Dirac equation. To study the effect of this imperfection, we have set S = π/2 + ΔS where ΔS takes 10% and 40% of the desired value, the result of which is depicted in Fig. 6a and b, respectively. The presence of the zero-mode persists upon experimental errors in creating the exact Hamiltonian. Another experimental imperfection that can affect the transmission spectrum is the loss. The loss from the excited states can be easily incorporated into the equation of motion by introducing an extra term −iγeff into Eq. (7)30, where γeff = γδ2/Ω2 with γ the decay rate from the excited states. Effects of photon losses are shown in Fig. 6c and d, where we have used δ(z) = δ0 tanh[0.02z] and  and 0.01, respectively. The transmission peak at the zero-mode reduces in size with increasing loss rate, but the peak is still visible at
and 0.01, respectively. The transmission peak at the zero-mode reduces in size with increasing loss rate, but the peak is still visible at  . Under normal EIT condition,
. Under normal EIT condition,  , which along with our numerical analysis indicates that the effect of the loss should not obstruct the detection of the zero-mode.
, which along with our numerical analysis indicates that the effect of the loss should not obstruct the detection of the zero-mode.
Discussion
In this work, we have shown that it is possible to simulate the Jackiw-Rebbi model and probe its topological nature in a driven slow-light system using current technology. By introducing spatially-dependent optical detunings, it is possible to simulate the Dirac equation with a spatially dependent static soliton field and allows one to directly probe the topologically protected zero-mode. The robustness of this zero-mode can be tested by changing the spatial profile of the detunings, while continuously observing the optical transmission spectrum of the system. We have also analysed the effects of experimental imperfections such as deviations from the ideal model and losses and showed that the observation of zero-mode survives these imperfections.
Before closing we would like to briefly comment on other types of models that might be studied in the same system in future works. Firstly, adding interactions in the system through EIT photon nonlinearities could allow the study of interesting strongly correlated physics. Intra-species repulsion would make the bosons behave like fermions in many ways and it would be interesting to think about how this affects the (lack of) charge fractionalisation effect in bosons. Interacting random mass Dirac model is another interesting possibility as studying the interplay between interactions and randomness is an important field being actively studied. Yet another possibility is to think of the mass term as the Lorentz-scalar potential which can act as a confining potential, given a proper spatial dependence61,62. This model has been shown to act as a phenomenological model of quark confinement motivated by the ‘MIT-bag’ model63.
References
Cirac, I. & Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 8, 264–266 (2012).
Blatt, R. & Roos, C. Quantum simulations with trapped ions. Nat. Phys. 8, 277–284 (2012).
Bloch, I., Dalibard, J. & Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267–276 (2012).
Hartmann, M., Brandão, F. G. S. L. & Plenio, M. B. Quantum many-body phenomena in coupled cavity arrays. Laser Photonics Rev. 2, 527 (2008).
Tomadin, A. & Fazio, R. Many-body phenomena in QED-cavity arrays. J. Opt. Soc. Am. B. 27, A130–A136 (2010).
Houck, A. Tureci, H. & Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 8, 292–299 (2012).
Angelakis, D. G., Santos, M. F. & Bose, S. Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays. Phys. Rev. A 76, 031805(R) (2007).
Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nat. Phys. 2, 849–855 (2006).
Greentree, A. D., Tahan, C., Cole, J. H. & Hollenberg, L. C. L. Quantum phase transitions of light. Nat. Phys. 2, 856–861 (2006).
Rossini, D. & Fazio, R. Mott-Insulating and Glassy Phases of Polaritons in 1D Arrays of Coupled Cavities. Phys. Rev. Lett. 99, 186401 (2007).
Cho, J., Angelakis, D. G. & Bose, S. Fractional Quantum Hall State in Coupled Cavities. Phys. Rev. Lett. 101, 246809 (2008).
Lukin, M. D. Colloquium: Trapping and manipulating photon states in atomic ensembles. Rev. Mod. Phys. 75, 457 (2003).
Fleischhauer, M., Imamoglu, A. & Marangos, J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633 (2005).
Bajcsy, M. et al. Efficient All-Optical Switching Using slow-light within a Hollow Fiber. Phys. Rev. Lett. 102, 203902 (2009).
Chang, D. E. et al. Crystallization of strongly interacting photons in a nonlinear optical fibre. Nat. Phys. 4, 884–889 (2008).
Angelakis, D. G., Huo, M.-X., Kyoseva, E. & Kwek, L. C. Luttinger Liquid of Photons and Spin-Charge Separation in Hollow-Core Fibers. Phys. Rev. Lett. 106, 153601 (2011).
Angelakis, D. G., Huo, M.-X., Chang, D., Kwek, L. C. & Korepin, V. Mimicking Interacting Relativistic Theories with Stationary Pulses of Light. Phys. Rev. Lett. 110, 100502 (2013).
Carusotto, I. et al. Fermionized Photons in an Array of Driven Dissipative Nonlinear Cavities. Phys. Rev. Lett. 103, 33601 (2009).
Grujic, T., Clark, S. R., Jaksch, D. & Angelakis, D. G. Non-equilibrium many-body effects in driven nonlinear resonator arrays. New J. Phys. 14, 103025 (2012).
Lamata, L., León, J., Schätz, T. & Solano, E. Dirac Equation and Quantum Relativistic Effects in a Single Trapped Ion. Phys. Rev. Lett. 98, 253005 (2007).
Gerritsma, R. et al. Quantum simulation of the Dirac equation. Nature 463, 68–71 (2010).
Casanova, J., García-Ripoll, J. J., Gerritsma, R., Roos, C. F. & Solano, E. Klein tunneling and Dirac potentials in trapped ions. Phys. Rev. A 82, 020101(R) (2010).
Gerritsma, R. et al. Quantum Simulation of the Klein Paradox with Trapped Ions. Phys. Rev. Lett. 106, 060503 (2011).
Longhi, S. Klein tunneling in binary photonic superlattices. Phys. Rev. B 81, 075102 (2010).
Dreisow, F. et al. Classical Simulation of Relativistic Zitterbewegung in Photonic Lattices. Phys. Rev. Lett. 105, 143902 (2010).
Keil, R. et al. The random mass Dirac model and long-range correlations on an integrated optical platform. Nature Comm. 4, 1368 (2012).
Juzellūnas, G., Ruseckas, J., Lindberg, M., Santos, L. & Öhberg, P. Quasirelativistic behavior of cold atoms in light fields. Phys. Rev. A 77, 011802(R) (2008).
Otterbach, J., Unanyan, R. G. & Fleischhauer, M. Confining Stationary Light: Dirac Dynamics and Klein Tunneling. Phys. Rev. Lett. 102, 063602 (2009).
Unanyan, R. G. et al. Spinor Slow-Light and Dirac Particles with Variable Mass. Phys. Rev. Lett. 105, 173603 (2010).
Ruseckas, J. et al. Photonic-band-gap properties for two-component slow-light. Phys. Rev. A 83, 063811 (2011).
Casanova, J. et al. Quantum Simulation of the Majorana Equation and Unphysical Operations. Phys. Rev. X 1, 021018 (2011).
Noh, C., Rodríguez-Lara, B. M. & Angelakis, D. G. Proposal for realization of the Majorana equation in a tabletop experiment. Phys. Rev. A 87, 040102(R) (2013).
Noh, C., Rodríguez-Lara, B. M. & Angelakis, D. G. Quantum simulation of neutrino oscillations with trapped ions. New J. Phys. 14, 033028 (2012).
Jackiw, R. & Rebbi, C. Solitons with fermion number . Phys, Rev. D 13, 3398 (1976).
Su, W. P., Shrieffer, J. R. & Heeger, A. J. Soliton excitations in polyacetylene. Phys. Rev. B 22, 2099 (1980).
Niemi, A. J. & Semenoff, G. W. Fermion number fractionization in quantum field theory. Phys. Rep. 135, 99–193 (1986).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Ruostekoski, J., Dunne, G. V. & Javanainen, J. Particle Number Fractionalization of an Atomic Fermi-Dirac Gas in an Optical Lattice. Phys. Rev. Lett. 88, 180401 (2002).
Javanainen, J. & Ruostekoski, J. Optical Detection of Fractional Particle Number in an Atomic Fermi-Dirac Gas. Phys. Rev. Lett. 91, 150404 (2003).
Yefsah, T. et al. Heavy solitons in a fermionic superfluid. Nature 499, 426–430 (2013).
Kitagawa, T. et al. Observation of topologically protected bound states in photonic quantum walks. Nat. Comm. 3, 882 (2012).
Hou, C.-Y., Chamon, C. & Mudry, C. Electron Fractionalization in Two-Dimensional Graphenelike Structures. Phys. Rev. Lett. 98, 186809 (2007).
Seradjeh, B. & Franz, M. Fractional Statistics of Topological Defects in Graphene and Related Structures. Phys. Rev. Lett. 101, 146401 (2008).
Romanonsky, I., Yannouleas, C. & Landman, U. Topological effects and particle physics analogies beyond the massless Dirac-Weyl fermion in graphene nanorings. Phys. Rev. B 87, 165431 (2013).
Malkova, N., Hromada, I., Wang, X., Bryant, G. & Chen, Z. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 34, 11, 1633–1635 (2009).
Ryu, S., Schnyder, A. P., Furusaki, A. & Ludwig, A. W. W. Topological insulators and superconductors: tenfold way and dimensional hierarchy. New J. Phys. 12, 065010 (2010).
Callias, C. Axial anomalies and index theorems on open spaces. Commun. math. Phys. 62, 213–234 (1978).
Prange, R. E. & Girvin, S. M. (eds.) The Quantum Hall Effect, 2nd ed. (Springer, Berlin, 1990).
Sarma, S. & Pinczuk, A. (eds.) Perspectives in Quantum Hall Effects (Wiley, New York, 1997).
Nayak, K. P. et al. Optical nanofiber as an efficient tool for manipulating and probing atomic Fluorescence. Opt. Express 15, 5431–5438 (2007).
Vetsch, E. et al. Optical Interface Created by Laser-Cooled Atoms Trapped in the Evanescent Field Surrounding an Optical Nanofiber. Phys. Rev. Lett. 104, 203603 (2010).
Ghosh, S., Sharping, J. E., Ouzounov, D. G. & Gaeta, A. L. Resonant Optical Interactions with Molecules Confined in Photonic Band-Gap Fibers. Phys. Rev. Lett. 94, 093902 (2005).
Takekoshi, T. & Knize, R. J. Optical Guiding of Atoms through a Hollow-Core Photonic Band-Gap Fiber. Phys. Rev. Lett. 98, 210404 (2007).
Christensen, C. A. et al. Trapping of ultracold atoms in a hollow-core photonic crystal fiber. Phys. Rev. A 78, 033429 (2008).
Vorrath, S., Möller, S. A., Windpassinger, P., Bongs, K. & Sengstock, K. Efficient guiding of cold atoms through a photonic band gap fiber. New J. Phys. 12, 123015 (2010).
Bajcsy, M. et al. Laser-cooled atoms inside a hollow-core photonic-crystal fiber. Phys. Rev. A 83, 063830 (2011).
Shahmoon, E., Kurizki, G., Fleischhauer, M. & Petrosyan, D. Strongly interacting photons in hollow-core waveguides. Phys. Rev. A 83, 033806 (2011).
Hafezi, M., Chang, D. E., Gritsev, V. Demler, E. A. & Lukin, M. D. Quantum transport of strongly interacting photons in a one-dimensional nonlinear waveguide. Phys. Rev. A 85, 013822 (2012).
Das, P., Noh, C. & Angelakis, D. G. Realization of the driven nonlinear Schrdinger equation with stationary light. Europhys. Lett. 103, 34001 (2013).
Critchfield, C. L. Scalar binding of quarks. Phys. Rev. D 12, 923 (1975).
Fishbane, P. M., Gasiorowicz, S. G., Johannsen, D. C. & Kaus, P. Vector and scalar confining potentials and the Klein paradox. Phys. Rev. D 27, 2433 (1983).
Chodos, A., Jaffe, R. L., Johnson, K., Thorn, C. B. & Weisskopf, V. New extended model of hadrons. Phys. Rev. D 9, 3741 (1974).
Acknowledgements
We would like to acknowledge the financial support provided by the National Research Foundation and Ministry of Education Singapore (partly through the Tier 3 Grant “Random numbers from quantum processes”) and travel support by the EU IP-SIQS.
Author information
Authors and Affiliations
Contributions
D.G.A. and C.N. developed the concept of the work. P.D. and C.N. have carried out numerical calculations. All authors have contributed to analysing the results and writing up the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Angelakis, D., Das, P. & Noh, C. Probing the topological properties of the Jackiw-Rebbi model with light. Sci Rep 4, 6110 (2014). https://doi.org/10.1038/srep06110
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06110
This article is cited by
-
Probing Chern number of quasicrystals with disorders in optical lattices
Quantum Information Processing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


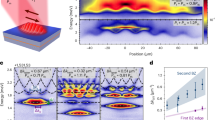






 and 0.01. The zero-mode peak survives all these experimental imperfections.
and 0.01. The zero-mode peak survives all these experimental imperfections.