Abstract
State of the art variable composition structure prediction based on density functional theory demonstrates that two new stoichiometries of PN, PN3 and PN2, become viable at high pressure. PN3 has a skutterudite-like Immm structure and is metastable with positive phonon frequencies at pressures between 10 and 100 GPa. PN3 is metallic and is the first reported nitrogen-based skutterudite. Its metallicity arises from nitrogen p-states which delocalise across N4 rings characteristic of skutterudites and it becomes a good electron-phonon superconductor at 10 GPa, with a Tc of around 18 K. The superconductivity arises from strongly enhanced electron-phonon coupling at lower pressures, originating primarily from soft collective P-N phonon modes. The PN2 phase is an insulator with P2/m symmetry and is stable at pressures in excess of 200 GPa.
Similar content being viewed by others
Introduction
High pressure synthesis offers a route to new materials with promising technological applications such as superconductors1,2,3,4 as well as to compounds with unexpected stoichiometries5. New theoretical structure prediction techniques6,7,8,9 have been used to identify novel superconductors by applying pressure to stoichiometries that form phases without the properties of superconductivity, metallicity or even stability at atmospheric pressure10,11,12,13,14,15. In spite of their great potential, nitride-based materials remain relatively unexplored due to the high stability of nitrogen molecules at ambient pressure; the strong N≡N triple bond results in a high kinetic barrier to polymerisation, thus extreme temperatures and pressures are required to synthesise many nitrides. However, at high pressures, the physical and chemical properties of nitrogen change substantially, allowing the formation of new polymeric crystalline phases16 and the possibility of forming new nitrogen-based superconducting crystals.
Nitride-based superconductors were among the first discovered and include examples with remarkably high superconducting critical temperatures (Tc), such as NbN (14.7 K)17 and β-HfNCl (25.5 K)18. However, in both instances, the superconductivity does not originate from the nitrogen atoms19 and the XNCl family of layered compounds have been proposed to be unconventional superconductors20.
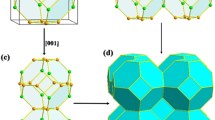
Another important example of superconductivity in pnictogen-based compounds involves the skutterudites, though, as far as we know, no nitrogen-based skutterudite has been found yet. They have the empirical formula TX3, where T is typically a transition metal and X is a pnictogen. They form a low density body-centred cubic  lattice consisting of dodecahedral cages (Fig. 1). This cage can be filled with a guest atom to form MT4X12,potentially changing the properties of the material, making it semiconducting21, paramagnetic22,superconducting23 or even thermoelectric24.They are also characterised by square X44− groups connecting the cages, which are thought to influence electrical conductivity and superconductivity25. Filled skutterudite superconducting materials have been synthesised under pressure26 and found to have high Tc values, for example LaRu4As12 with Tc = 10.3 K26 and La0.6Rh4P12 with Tc = 17 K, the highest known among metal phosphides27. It has been shown that although the guest atom in filled skutterudites stabilises the lattice, the superconductivity is an intrinsic property of the T4X12 framework28,29.
lattice consisting of dodecahedral cages (Fig. 1). This cage can be filled with a guest atom to form MT4X12,potentially changing the properties of the material, making it semiconducting21, paramagnetic22,superconducting23 or even thermoelectric24.They are also characterised by square X44− groups connecting the cages, which are thought to influence electrical conductivity and superconductivity25. Filled skutterudite superconducting materials have been synthesised under pressure26 and found to have high Tc values, for example LaRu4As12 with Tc = 10.3 K26 and La0.6Rh4P12 with Tc = 17 K, the highest known among metal phosphides27. It has been shown that although the guest atom in filled skutterudites stabilises the lattice, the superconductivity is an intrinsic property of the T4X12 framework28,29.
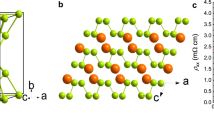
The skutterudite-like Immm structure of PN3 in its body-centred orthorhombic conventional cell.
The skutterudite structure has  symmetry, but the PN3 phase is characterised by an orthorhombic distortion. Phosphorus atoms are six-coordinated in both cases. Phosphorus atoms are yellow and nitrogen atoms purple.
symmetry, but the PN3 phase is characterised by an orthorhombic distortion. Phosphorus atoms are six-coordinated in both cases. Phosphorus atoms are yellow and nitrogen atoms purple.
In this article we perform a systematic search for thermodynamically stable phosphorus nitrides under pressure using evolutionary structure prediction and density functional theory (DFT). Beyond the only known stable phosphorus nitride, P3N5, which forms a variety of pressure-dependent phases30,31,32,33, we find that a novel phosphorus nitride skutterudite (PN3) containing six-coordinated phosphorus can be formed at undemanding pressures (~10 GPa). PN3 is the first reported nitrogen-based skutterudite. It is metallic, metastable and dynamically stable between 10 and 100 GPa. Although it is unstable at ambient pressure, it may be possible to stabilise it using off-stoichiometry doping with a guest species at the centre of the cage, as with other skutterudite superconductors. PN3 is a good superconductor with a Tc of around 18 K at 10 GPa, higher than for any known skutterudite. We also report the discovery of a new insulating phase with PN2 stoichiometry, which is stable above 200 GPa.
Results
High pressure phosphorus nitride structures
In the first instance, fixed composition searches were performed using one and two formula units of P3N5 at pressures of 25 GPa, 50 GPa, 100 GPa and 200 GPa, yielding the Imm2 γ-phase at lower pressures and the previously predicted C2/c oxyvanite phase at high pressures, in agreement with the findings of Dong et al.34 The recovery of an experimentally verified phase in addition to a structure predicted through chemical intuition is a reassuring vindication of the USPEX code. According to the results presented in Fig. 2, the α phase, which is stable at ambient pressure, undergoes a transition to the γ phase at around 7 GPa, which transforms to the oxyvanite phase at 34 GPa. The previously predicted δ′ phase35 is at least 0.2 eV higher in enthalpy than γ.
Variable composition searches were performed at 100 GPa in order to identify potential stable stoichiometries; these were followed by fixed composition searches for the best stoichiometries at pressures of 25 GPa, 50 GPa, 100 GPa and 200 GPa using PN3, PN2, P3N4, P3N5 and PN. The resulting convex hull is shown in the upper panel of Fig. 3, illustrating the most stable compositions: PN3, PN2 and P3N5. The enthalpies of the most interesting structures are plotted at different pressures in the lower panel. A new insulating P2/m phase of PN2 (structure in Fig. 4 and electronic density of states in Fig. 5) becomes stable with respect to N and P3N5 at pressures in excess of 200 GPa, while the best PN3 structure (Immm) is very close to the hull below 100 GPa. It is noteworthy that both new structures consist of octahedral PN6 units, containing octahedral six-coordinated phosphorus atoms; this was unprecedented until a pressure induced transition to six-coordinated phosphorus was observed in AlPO4 as a densification mechanism36. The structural parameters for these two new structures are listed in Table I.
Convex hull for the PxN1−x system at 100 GPa (top) and at different pressures (bottom).
H is the enthalpy per atom of the generated structure, H[P] the enthalpy per atom of the stable phosphorus phase (simple hexagonal phosphorus at 100 GPa) and H[N] is the enthalpy per atom of the stable nitrogen phase (cubic gauche nitrogen at 100 GPa). The lower panel only includes the Immm-PN3, P2/m-PN2 and oxyvanite-P3N5 structures.
The Immm-PN3 skutterudite
The skutterudite-like PN3 is formed from dodecahedral cages (Fig. reffig:Immm-structure) consisting of six-coordinated phosphorus atoms at the vertices of a cuboid, with the faces occupied by N2 pairs, forming pentagonal rings. In contrast with all other known and predicted PN structure, the nitrogen atoms are all three-coordinated, compared with the γ, oxyvanite and new P2/m phases, which contain both three- and four-coordinated nitrogens. Surprisingly, the N–N bonds are extremely short; at 100 GPa, they are 1.28 Å, increasing to 1.30 Å at 10 GPa. No other structures were found with such a short bond length. As the pressure decreases, the orthorhombic distortion in the Immm cell becomes more pronounced in the b direction, causing the structure to break down; it is likely that this is thermodynamically favourable since the N2 units are very close in geometry to their configuration in the gas phase. However, the structure is dynamically stable with well-defined positive phonons at pressures as low as 10 GPa. Thus the possibility remains that the skutterudite structure may be synthesised at moderate pressures.
MX3 skutterudites are also characterised by six square X4 rings in the conventional 32-atom cell. In PN3, these rings are rectangular rather than square as a result of the orthorhombic distortion, but can be discerned as pairs of N2 units separated by 1.9 Å at 100 GPa, which could be either a weak bond or a non-bonding contact. A Bader analysis reveals that the nitrogens have little ionic character, with a charge of 0.065 to 0.075e. These X4 rings have been shown to give rise to conduction and superconductivity in other skutterudites, namely CoP3 and NiP337 and LaFe4P1225.
PN3 is metallic throughout its stable pressure range. There is a distinct set of three bands (Fig. 6) dispersing from approximately 1 eV below  to 2 eV above
to 2 eV above  responsible for the conductivity. The partial density of states (Fig. 6) demonstrates that the dominant contribution to the conducting bands arises from nitrogen 2p atomic orbitals. It is interesting to note that in electronic structure calculations of other metallic skutterudites, namely CoP3 and NiP3, the highest occupied bands consist of phosphorus centred p-orbitals37, which occupy analogous positions to nitrogen in PN3, phosphorus being isoelectronic to nitrogen.
responsible for the conductivity. The partial density of states (Fig. 6) demonstrates that the dominant contribution to the conducting bands arises from nitrogen 2p atomic orbitals. It is interesting to note that in electronic structure calculations of other metallic skutterudites, namely CoP3 and NiP3, the highest occupied bands consist of phosphorus centred p-orbitals37, which occupy analogous positions to nitrogen in PN3, phosphorus being isoelectronic to nitrogen.
The three bands around the Fermi level were projected onto maximally localised Wannier functions (MLWF), as illustrated in Fig. 7. The Wannier projections have p-orbital-like symmetry, but are delocalised across N2 pairs which form adjacent skutterudite N4 rings, accounting for the conductivity.
Phonon spectra and electron-phonon coupling in the Immm-PN3 skutterudite
The phonon spectra of PN3 (Fig. 8) are characterised by two groups of modes; firstly dispersive low-energy modes that involve collective vibrations of P and N atoms. These modes are separated from the second group, high-energy Einstein-like modes, primarily corresponding to vibrations of the short N−N bonds, by a distinct gap. As the pressure is lowered, the acoustic modes and some low-energy optical modes related to distortions of the whole dodecahedral cage are softened. This gives rise to a structural instability at ambient pressure as the lowest energy mode at the X and R point acquire an imaginary frequency. The instability is related to the decomposition of PN3 and the formation of N2 pairs. Structurally, this is manifested as the formation of PN “sheets” enclosing N2 molecules and is reflected by significant changes in the phonon dispersion. However, at 10 GPa the phonon spectrum does not display any imaginary frequencies and the crystal structure is dynamically stable.
The electron-phonon coupling constant λ, calculated from equation (3), scales linearly with the density of states at the Fermi level and is inversely proportional to the square of the phonon frequencies. Its calculated values are presented in Table II and the Eliashberg functions are plotted in Fig. 9. At all pressures studied, the eDOS at  remains high due to the presence of weakly dispersive bands in the vicinity of the Fermi level (Fig. 6). This ensures a large electronic contribution to the Eliashberg functions coming from the double electronic Dirac delta in equation (1). Thus, the evolution of λ under pressure is mostly determined by the evolution of the phonon spectra.
remains high due to the presence of weakly dispersive bands in the vicinity of the Fermi level (Fig. 6). This ensures a large electronic contribution to the Eliashberg functions coming from the double electronic Dirac delta in equation (1). Thus, the evolution of λ under pressure is mostly determined by the evolution of the phonon spectra.
At 10 GPa the electron-phonon coupling constant reaches a remarkable value of 1.05. The low-energy modes (<400 cm−1) contribute more strongly to λ due to their low frequencies. This is evidenced by the strong contribution of the low-energy part of the Eliashberg function to λ, demonstrated in Fig. 9. The contribution to λ of the lowest energy acoustic mode at the R special point is particularly large. At 20 GPa, the electron-phonon coupling decreases as low-frequency modes gain energy. This causes the strong peaks in α2F(ω) at low energy to shift to higher frequencies and thus reduces their contribution to λ. At higher pressures, the energy of the lowest energy acoustic mode at R is strongly increased and, consequently, its contribution to λ is strongly suppressed, inducing a considerable reduction of the electron-phonon coupling constant.
Using the computed values of the electron-phonon coupling constant, we estimated the superconducting Tc using the standard values of μ* = 0.10 and μ* = 0.13 for the Coulomb pseudopotential in equation (2). These values are summarised in Table II. Tc reaches 18.6 K for μ* = 0.10 at 10 GPa, a high value for an electron-phonon coupling superconductor. Using μ* = 0.13, a slightly lower but similar 16.1 K value is obtained, showing that for large values of λ Tc is weakly dependent on μ*. The evolution of Tc is consistent with the pressure dependence of λ and both are suppressed at high pressures.
Inclusion of a guest atom in the skutterudite lattice
Filled skutterudites are of particular interest for their potential thermoelectric properties. If the void in a skutterudite cage is significantly larger than the guest atom, then the vibrational modes of the guest atom are expected to be strongly anharmonic, resulting in “rattling modes”24. These modes tend to reduce thermal conductivity by scattering the phonons responsible for heat transport38 and, consequently, enhance the figure of merit of thermoelectric materials39. We now turn to the question of whether the skutterudite remains stable when it hosts such a guest atom.
It should be noted that the cage in PN3 is considerably smaller than for other skutterudites, which are large enough to hold atoms such as barium, which has a covalent radius of 2.53 Å. PN3 has a body-centred orthorhombic lattice at lower pressures, in contrast with most skutterudites which are body-centred cubic; the distance between the body centre of the cage and the closest point on the surface of the cage (specifically, the midpoint of a N2 bond) is 1.81 Å, compared with 2.79 Å for CoAs3. This greatly limits the choice of guest atom to smaller species such as hydrogen, lithium and beryllium.
A beryllium atom proved to be too large, resulting in imaginary frequencies throughout the Brillouin zone. A lone hydrogen atom was too thermodynamically unstable to occupy the body centre of the lattice, drifting towards a phosphorus atom during geometry optimisation and breaking the Immm symmetry. The phonon dispersion for PN3 with a lithium guest has a soft mode at the X special point and is therefore not stable; this was the case through the pressure range 10–100 GPa. In conclusion, it seems there is no stable XP4N12 filled skutterudite.
The inclusion of a guest atom and a reduction of the external pressure have a similar effect on the atomic structure: the guest atom forces the cage to expand, just as the structure loses its dynamical stability as the lattice parameter increases at pressures below 10 GPa. It may be possible to stabilise the structure by doping the system with, for example, one lithium atom per eight conventional cells (i.e. a 2 × 2 × 2 supercell), although this would necessitate phonon calculations that would be prohibitively expensive.
Discussion
In conclusion, we used density functional theory coupled with evolutionary structure prediction to explore the variable composition configuration space of phosphorus nitride. We identified a new stable stoichiometry, insulating PN2 with P2/m symmetry, at pressures in excess of 200 GPa and a fascinating new metastable structure, PN3, which is dynamically stable between approximately 10 and 100 GPa.
The PN3 structure has Immm symmetry, belongs to the  skutterudite class of compounds and is the first to contain nitrogen as pnictogen. It is characterised by an orthorhombic distortion, the extent of which increases as the pressure is decreased. Skutterudite-PN3 is metallic throughout the range of pressures examined, 10–100 GPa, its electrical conductivity arising from the delocalisation of nitrogen p-states across N4 rings. Most significantly, it becomes a good electron-phonon superconductor with a Tc of around 18 K at 10 GPa due to strong electron-phonon coupling with low-frequency phonon modes. At higher pressures the superconducting Tc is suppressed as low-energy acoustic modes gain energy. The superconducting behavior of PN3 is comparable to other high-pressure superconductors such as Te, Li and S, where the evolution of Tc under pressure is determined by the behavior of low-energy phonon modes and is enhanced close to dynamical instabilities40,41,42.
skutterudite class of compounds and is the first to contain nitrogen as pnictogen. It is characterised by an orthorhombic distortion, the extent of which increases as the pressure is decreased. Skutterudite-PN3 is metallic throughout the range of pressures examined, 10–100 GPa, its electrical conductivity arising from the delocalisation of nitrogen p-states across N4 rings. Most significantly, it becomes a good electron-phonon superconductor with a Tc of around 18 K at 10 GPa due to strong electron-phonon coupling with low-frequency phonon modes. At higher pressures the superconducting Tc is suppressed as low-energy acoustic modes gain energy. The superconducting behavior of PN3 is comparable to other high-pressure superconductors such as Te, Li and S, where the evolution of Tc under pressure is determined by the behavior of low-energy phonon modes and is enhanced close to dynamical instabilities40,41,42.
The phonon dispersion at 10 GPa shows no sign of instability, opening the door to the possibility of its synthesis, perhaps by chemical synthesis from precursors in the correct ratio, or thin film deposition on a substrate with a similar lattice parameter. Furthermore, although the dodecahedral cage is too small to host one guest atom (H, Li, Be) per primitive cell, it may be possible to stabilise the PN3 lattice at ambient pressure using off-stoichiometry doping with a guest species.
Methods
The USPEX code6,7 was used in conjunction with DFT to determine the most thermodynamically stable PN crystal structures for several different compositions. USPEX employs evolutionary algorithms to find the atomic structure with the lowest enthalpy at a given pressure, given knowledge only of the chemical composition of the unit cell. It has been employed with great success with many other systems at high pressure43,44,45,46.
All structures were optimised with the CASTEP DFT code47 at the GGA level, using the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional48. All lattice parameters and atomic positions were relaxed without constraints until forces varied by less than 0.05 eV Å−1 and energies by less than 1 × 10−5 eV between BFGS steps. SCF steps were considered to be converged when the total energy varied by less than 1 × 10−6 eV between steps. Electronic wavefunctions were expanded using a plane wave basis set with a cutoff of 350 eV and core electrons (1s2 in the case of N and 1s22s22p6 in the case of P) were represented with ultrasoft pseudopotentials. Monkhorst-Pack grids were generated per cell, using a spacing of 2π × 0.05 Å−1. Ultrasoft pseudopotentials were employed with the intention of minimising calculation times; the nitrogen potential in particular had a core radius of 1.4 a0, which may have resulted in core overlap in the case of structures with extremely short N−N bonds; however, enthalpies were compared with a hard reference pseudopotential with a 1.0 a0 core radius and the results found to be consistent.
Phonon and electron-phonon calculations were performed on the 16-atom primitive cell of the Immm skutterudite structure using density-functional perturbation theory (DFPT)49 as implemented in the Quantum Espresso code50. Ultrasoft pseudopotentials, a plane wave cutoff of 60 Ry, a density cutoff of 600 Ry and a 4 × 4 × 4 Monkhorst-Pack grid for the electronic integrations were used throughout. The cell was fully reoptimised using the new pseudopotentials and selected conduction bands were projected onto maximally localised Wannier functions (MLWF) using the wannier90 code51,52. Phonon frequencies and electron-phonon coefficients were calculated on a 2 × 2 × 2 q-point grid.
The Eliashberg functions of the electron-phonon coupling were calculated as

In Eq. (1) is the electron-phonon matrix element, where |kn〉 is a Kohn-Sham state with energy
is the electron-phonon matrix element, where |kn〉 is a Kohn-Sham state with energy  measured from the Fermi level (
measured from the Fermi level ( ), Nk and Nq are the number of electron and phonon momentum points used for the Brillouin zone sampling, N(0) is the density of states per spin at
), Nk and Nq are the number of electron and phonon momentum points used for the Brillouin zone sampling, N(0) is the density of states per spin at  , V is the self-consistent Kohn-Sham potential, usα(q) is the Fourier transformed displacement from equilibrium of atom s along Cartesian direction α, Ms is the mass of atom s and ωμ(q) and
, V is the self-consistent Kohn-Sham potential, usα(q) is the Fourier transformed displacement from equilibrium of atom s along Cartesian direction α, Ms is the mass of atom s and ωμ(q) and  are respectively phonon frequency and polarisations with momentum q. A finer 12 × 12 × 12 mesh was used in the sum over k-points in Eq. (1). Superconducting Tc values were estimated from the Allen-Dynes modified McMillan equation53:
are respectively phonon frequency and polarisations with momentum q. A finer 12 × 12 × 12 mesh was used in the sum over k-points in Eq. (1). Superconducting Tc values were estimated from the Allen-Dynes modified McMillan equation53:

where the electron-phonon coupling constant is calculated as

the logarithmic frequency average is  and μ* is the Coulomb pseudopotential parameter.
and μ* is the Coulomb pseudopotential parameter.
References
McMillan, P. F. New materials from high-pressure experiments. Nature Mater 1, 19 (2002).
Solozhenko, V. L. & Gregoryanz, E. Synthesis of superhard materials. Mater. Today 8, 44 (2005).
McMillan, P. F. High-pressure synthesis of materials. In: High-Pressure Crystallography: from fundamental phenomena to technological applications, 373 (Springer, 2010).
Zerr, A., Miehe, G. & Riedel, R. Synthesis of cubic zirconium and hafnium nitride having Th3P4 structure. Nature Mater. 2, 185 (2003).
Zhang, W. et al. Unexpected stable stoichiometries of sodium chlorides. Science 342, 1502 (2013).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys. 124, 244704 (2006).
Oganov, A. R. & Glass, C. W. Evolutionary crystal structure prediction as a tool in materials design. J. Phys.: Condens. Matter 20, 064210 (2008).
Pickard, C. J. & Needs, R. J. Ab initio random structure searching. J. Phys.: Condens. Matter 23, 053201 (2011).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Buzea, C. & Robbie, K. Assembling the puzzle of superconducting elements: a review. Supercond. Sci. Technol. 18, R1 (2005).
Xie, Y., Oganov, A. R. & Ma, Y. Novel high pressure structures and superconductivity of CaLi2 . Phys. Rev. Lett. 104, 177005 (2010).
Martinez-Canales, M. et al. Novel structures and superconductivity of silane under pressure. Phys. Rev. Lett. 102, 087005 (2009).
Gao, G. et al. Dissociation of methane under high pressure. Proc. Natl. Acad. Sci. USA 107, 1317 (2010).
Zhu, L. et al. Substitutional alloy of bi and te at high pressure. Phys. Rev. Lett. 106, 145501 (2011).
Errea, I., Martinez-Canales, M. & Bergara, A. Ab initio study of superconducting hexagonal Be2Li under pressure. Phys. Rev. B 78, 172501 (2008).
Raza, Z., Pickard, C. J., Pinilla, C. & Saitta, A. M. High energy density mixed polymeric phase from carbon monoxide and nitrogen. Phys. Rev. Lett. 111, 235501 (2013).
Matthias, B. T. & Hulm, J. K. A search for new superconducting compounds. Phys. Rev. 87, 799 (1952).
Yamanaka, S., Hotehama, K. & Kawaji, H. Superconductivity at 25.5 k in electron-doped layered hafnium nitride. Nature Lett. 392, 580 (1998).
Wang, C. et al. First-principles calculations on the mechanical properties of niobium nitrides. Solid State Commun. 149, 725 (2009).
Taguchi, Y., Kitora, A. & Iwasa, Y. Increase in tc upon reduction of doping in LixZrNCl superconductors. Phys. Rev. Lett. 97, 107001 (2006).
Sofo, J. O. & Mahan, G. D. Electronic structure of CoSb3: a narrow-band-gap semiconductor. Phys. Rev. B 58, 620 (1998).
Möchel, A. et al. Lattice dynamics in the FeSb3 skutterudite. Phys. Rev. B 84, 064302 (2011).
Meisner, G. P. Superconductivity and magnetic order in ternary rare earth transition metal phosphides. Physica B + C 108, 763 (1981).
Slack, G. A. & Tsoukala, V. G. Some properties of semiconducting IrSb3 . J. Appl. Phys. 76, 1665 (1994).
Jung, D., Whangbo, M. & Alvarex, S. Importance of the X4 ring orbitals for the semiconducting, metallic, or superconducting properties of skutterudites MX3 and RM4X12 . Inorg. Chem. 29, 2252 (1990).
Shirotani, I. et al. Superconductivity of filled skutterudites LaRu4As12 and PrRu4As12 . Phys. Rev. B 56, 7866 (1997).
Shirotani, I. et al. Superconductivity of the new skutterudite compound LaxRh4P12 at high pressure. J. Phys.: Condens. Matter 17, 7353 (2005).
Bauer, E. et al. Superconductivity in novel ge-based skutterudites: {Sr,Ba}Pt4Ge12 . Phys. Rev. Lett. 99, 217001 (2007).
Bauer, E. et al. Superconductivity and spin fluctuations in {Th,U}Pt4Ge12 skutterudites. Phys. Rev. B 78, 064516 (2008).
Bettermann, G., Krause, W., Riess, G. & Hofmann, T. Phosphorus compounds, inorganic. Ullman's Encyclopedia of Industrial Chemistry 27, 1 (2012).
Schnick, W., Lu, J. & Krumeich, F. Phosphorus nitride P3N5: synthesis, spectroscopic and electron microscopic investigations. Chem. Mater. 8, 281 (1996).
Horstmann, S., Irran, E. & Schnick, W. Synthesis and crystal structure of phosphorus (v) nitride α-P3N5 . Angew. Chem. Int. Ed. 36, 1873 (1997).
Landskron, K., Huppertz, H., Senker, J. & Schnick, W. High-pressure sysnthisis of γ-P3N5 at 11 gpa and 1500°c in a multianvil assembly: a binary phosphorus (v) nitride with a three-dimensional network structure from PN4 tetrahedra and tetragonal PN5 pyramids. Angew. Chem. Int. Ed. 40, 2643 (2001).
Dong, J., Kinkhabwala, A. A. & McMillan, P. F. High-pressure polymorphism in phosphorus nitrides. Phys. Status Solidi (B) 241, 2319 (2004).
Kroll, P. & Schnick, W. A density functional study of phosphorus nitride P3N5: refined geometries, properties and relative stability of α-P3N5 and γ-P3N5 and a further possible high-pressure phase δ-P3N5 with kyanite-type structure. Chem. Eur. J. 8, 3530 (2002).
Pellicer-Porres, J., Saitta, A. M., Polian, A., Itié, J. P. & Hanfland, M. Six-fold-coordinated phosphorus by oxygen in AlPO4 quartz homotype under pressure. Nature Mater. 6, 698 (2007).
Llunell, M., Alemany, P., Alvarez, S., Vernes, A. & Zhukov, V. P. Electronic structure and bonding in skutterudite-type phosphides. Phys. Rev. B 53, 10605 (1996).
Vining, C. B. Half-full glasses: the new black. Nature Mater. 7, 765 (2008).
Mihaly, L. Crystal cages for clean coolers. Nature 395, 839 (1998).
Mauri, F., Zakharov, O., de Gironcoli, S., Louie, S. G. & Cohen, M. L. Atomic structure of icosahedral B4C boron carbide from a first principles analysis of nmr spectra. Phys. Rev. Lett. 77, 1151 (1996).
Profeta, G. et al. Superconductivity in lithium, potassium and aluminium under extreme pressure: a first-principles study. Phys. Rev. Lett. 96, 047003 (2006).
Degtyareva, O. et al. Competition of charge-density waves and superconductivity in sulfur. Phys. Rev. Lett. 99, 155505 (2007).
Oganov, A. R. et al. Ionic high-pressure form of elemental boron. Nature 457, 863 (2009).
Ma, Y. et al. Transparent dense sodium. Nature 458, 182 (2009).
Oganov, A. R. et al. Exotic behavior and crystal structures of calcium under pressure. Proc. Natl. Acad. Sci. USA 107, 7646 (2010).
Oganov, A. R., Glass, C. W. & Ono, S. High-pressure phases of CaCO3: crystal structure prediction and experiment. Earth Planet Sci. Lett. 241, 95 (2006).
Clark, S. J. et al. First principles methods using castep. Z. Kristall. 220, 567 (2005).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Giannozzi, P. et al. Quantum Espresso: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised wannier functions. Comp. Phys. Comm. 178, 685 (2008).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905 (1975).
Acknowledgements
Z.R. and A.M.S. acknowledge the GENCI IDRIS French National supercomputing facility for CPU time (Project Grant No. 91387) and thank the French Agence Nationale de la Recherche (ANR) for support through Project No. ANR-2011-BS08-018. I.E. would like to acknowledge financial support from the Department of Education, Language Policy and Culture of the Basque Government (Grant No. BFI-2011-65). A.R.O. thanks the National Science Foundation (EAR-1114313, DMR-1231586), DARPA (Grants No. W31P4Q1210008 and W31P4Q1310005), the Government (No. 14.A12.31.003) and the Ministry of Education and Science of the Russian Federation (Project No. 8512) for financial support and Foreign Talents Introduction and Academic Exchange Program (No. B08040).
Author information
Authors and Affiliations
Contributions
Z.R. and I.E. performed the calculations, A.R.O. and A.M.S. contributed to the analysis. Z.R. and I.E. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Raza, Z., Errea, I., Oganov, A. et al. Novel superconducting skutterudite-type phosphorus nitride at high pressure from first-principles calculations. Sci Rep 4, 5889 (2014). https://doi.org/10.1038/srep05889
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05889
This article is cited by
-
Rich stoichiometries of stable Ca-Bi system: Structure prediction and superconductivity
Scientific Reports (2015)
-
Pressure-induced zigzag phosphorus chain and superconductivity in boron monophosphide
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

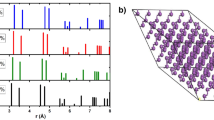







 at 100 GPa The orbital is spread over skutterudite N4 rings, giving rise to electronic conductivity.
at 100 GPa The orbital is spread over skutterudite N4 rings, giving rise to electronic conductivity.

 for the Immm phase at 10 GPa, 20 GPa, 50 GPa and 100 GPa.
for the Immm phase at 10 GPa, 20 GPa, 50 GPa and 100 GPa.