Abstract
In high-transition-temperature superconducting cuprates and iron arsenides, chemical doping plays an important role in inducing superconductivity. Whereas in the cuprate case, the dominant role of doping is to inject charge carriers, the role for the iron arsenides is complex owing to carrier multiplicity and the diversity of doping. Here, we present a comparative study of the in-plane resistivity and the optical spectrum of doped BaFe2As2, which allows for separation of coherent (itinerant) and incoherent (highly dissipative) charge dynamics. The coherence of the system is controlled by doping and the doping evolution of the charge dynamics exhibits a distinct difference between electron and hole doping. It is found in common with any type of doping that superconductivity with high transition temperature emerges when the normal-state charge dynamics maintains incoherence and when the resistivity associated with the coherent channel exhibits dominant temperature-linear dependence.
Similar content being viewed by others
Introduction
High-transition-temperature (high-Tc) superconductivity in iron arsenides is induced by various doping (chemical substitution) processes into metallic parent compounds showing an antiferromagnetic-orthorhombic (AFO) order. For a representative parent iron arsenide BaFe2As2, the superconducting (SC) phase is attained by doping into all the three different lattice sites1,2,3 and even by isovalent atomic substitution, e.g., P for As3 and Ru for Fe4. Notably, both electron and hole doping can generate superconductivity, in stark contrast to the case of high-Tc cuprates, in which only one type of carrier doping can induce superconductivity for one parent compound and superconductivity is not achieved by substituting Ni or Zn for Cu in Mott insulating parent compounds.
The mechanism of various doping processes leading to the emergence of superconductivity is a matter of debate. Charge carriers appear to be supplied as revealed by the study of angle-resolved photoemission spectroscopy (ARPES), which demonstrates that the electron Fermi surface (FS) expands (the hole FS shrinks) for electron doping (e.g., Co substitution for Fe)5,6 and vice versa for hole doping (e.g., K substitution for Ba)7. However, how this contrasting doping evolution of the FS is reflected in charge transport has not been seriously studied. More fundamentally, the question of how a change in electron/hole density in already metallic parent compounds alters the electronic environment to favor superconductivity or whether the change in carrier density is really an important ingredient for superconductivity is nontrivial. In addition to the change in carrier density, a chemical-pressure effect also has a significant influence on the electronic structure8,9,10. To gain a deeper understanding of the physics of doping in iron-based superconductors, it is of fundamental importance to extract universal natures such as the necessary ingredients for superconductivity among different doping processes. Because doping into BaFe2As2 covers the entire doping range from the AFO to the SC phase and further to the metallic non-SC end compounds, it is a suitable system for investigating the physical implications of doping.
Optical spectroscopy is a bulk-sensitive and energy-resolved probe and turns out to be a powerful tool to study charge dynamics and its evolution with doping in a multi-carrier system, particularly iron pnictides. The optical conductivity spectrum of iron arsenides is characterised by a small zero-energy peak, corresponding to a relatively coherent carrier dynamics and a long tail extending to a high-energy region, indicative of the presence of an incoherent charge dynamics with large spectral weight11,12,13,14,15. Such a spectral feature is also seen in the spectrum of the high-Tc cuprates and characterises the normal-state charge dynamics in high-Tc superconductors. The combination of resistivity and optical conductivity makes it possible to separate the contribution of multiple carriers or to separate a coherent component from an incoherent one in charge dynamics by disentangling the carrier scattering rate from the carrier density. Indeed, the decomposition of the spectrum for Codoped BaFe2As2 explains the temperature and doping dependence of the charge dynamics well12.
Here, we show how the magnitude and the temperature (T) dependence of the in-plane resistivity ρ(T) evolve with doping (chemical substitution) into the three different sites in the parent compound BaFe2As2: Ba(Fe1−xCox)2As2, BaFe2(As1−xPx)2 and Ba1−xKxFe2As2 (abbreviated as Co-Ba122, P-Ba122 and K-Ba122, respectively). In the present study, we focus on the effect of doping in the high-temperature paramagnetic-tetragonal (PT) phase. The results of the doping evolution of resistivity and optical conductivity spectrum indicate that a dominant effect is to control coherence/incoherence in charge dynamics in different ways depending on the dopant sites/species. Superconductivity is found to emerge when the normal-state charge dynamics maintains incoherence. It is also found from the analysis of the T dependence of resistivity that, in the region of superconductivity showing fairly high Tc values, the normal-state resistivity is dominated by the T-linear scattering term.
Results
Doping evolution of in-plane resistivity
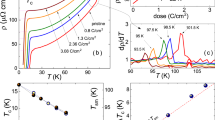
Figure 1 shows the doping evolution of ρ(T) for the three systems, Co-, P- and K-Ba122. The undoped parent compound BaFe2As2, the quality of which is remarkably improved by annealing, shows very low residual resistivity (< 10 µΩcm) at low temperatures in the AFO phase and the AFO-PT transition temperature Ts is 143 K, the highest among the temperatures so far reported16,17. Nevertheless, the resistivity at 300 K is fairly high, ~340 µΩcm and is comparable with that for unannealed crystals. The T dependence is weak in the PT phase above Ts, suggesting that the charge carriers are highly incoherent. The resistivity in the PT phase rapidly decreases with Co and P doping, in sharp contrast with that in the AFO phase, where the resistivity increases with doping, indicating that doping plays different roles in the two phases. In contrast, the change in magnitude is moderate in the case of K doping.
The evolution of ρ(T) with Co doping is basically the same as that reported by Rullier-Albenque et al.18, except for a significantly lower resistivity in the AFO phase in the present result. With Co doping, the temperature dependence changes from T linear to T2 in the overdoped non-SC region. Note that a fairly large residual resistivity remains up to x = 0.24, indicating that a doped Co atom works as a relatively stronger scattering center. The substitution of P for As corresponds to chemically isovalent doping. The number of electrons and holes is expected to be balanced over the entire range of doping. Controversially, as in the case of Co-Ba122, the magnitude of the resistivity in the PT phase monotonically decreases with P doping and the T dependence gradually changes from T-linear to T2, in agreement with the result obtained by Kasahara et al.3. A difference is that a doped P atom is a weaker scattering center as evidenced by a smaller residual-resistivity component. The doping evolution of ρ(T) in K-Ba122 is in sharp contrast to the Co- and P-doping cases19,20. Chemically, K doping corresponds to hole doping, but both the magnitude and T dependence of the resistivity only weakly change with doping. At low temperatures and at any doping level, the resistivity rapidly decreases with decreasing temperature, showing the T2 dependence typical of a Fermi liquid, whereas it shows a clear tendency for saturation in the high-temperature PT phase. As far as the high-T region is concerned, even the end compound KFe2As2 with Tc ~ 3.5 K is not a good metal. Although a finite residual resistivity appears for the compounds showing the AFO order (x ≤ 0.23), the magnitude of the residual resistivity for the K-doped compounds is considerably small compared with the Co- and P-doping cases, probably because a doped K atom is located farthest away from the Fe plane.
Doping evolution of optical conductivity spectrum
Figure 2(a) displays the optical conductivity spectrum of BaFe2As2. The spectrum shows a small peak at ω = 0 and a long tail merging into a broad peak in the higher-energy region. Using the Drude–Lorentz model, we decompose the spectrum as shown in Fig. 2(a). Because a single Drude component cannot reproduce the low-energy spectrum well, we decomposed the spectrum using two Drude components12,14,15,21,22,23. Given that iron pnictides are multiband systems, the presence of multiple Drude components is a valid result. The black and orange lines indicate the experimental and fitting results, respectively. The low-energy conductivity is dominated by two Drude components with distinct characteristics: one is narrow with a small spectral weight (in blue) and the other is broad with a much larger spectral weight (in gray). A higher-energy component approximated by a Lorentzian function (in green) corresponds to an interband excitation.
The width of the broad Drude component (the scattering rate 1/τ) is ~2000 cm−1, corresponding to τ = 1.7 × 10−14 s. From the band dispersions of BaFe2As2 obtained by ARPES measurements24, it is seen that the Fermi velocity vF of the band with a heavier effective mass is much less than 1.0 × 106 cm/s. From this, the mean free path l ( = vFτ) for the broad Drude component is estimated to be less than 1.7 Å, which is significantly shorter than the shortest interatomic spacing (2.4 Å). On the other hand, for the narrow Drude component with a width of ~200 cm−1, we estimate the Fermi velocity to be  and hence the mean free path to be
and hence the mean free path to be  . It is considerably longer than the lattice parameter (
. It is considerably longer than the lattice parameter ( ), which indicates relatively coherent charge dynamics. Hereafter, we call the narrow and broad Drude components the coherent and incoherent components (σD and σin), respectively. The incoherent component turned out to be nearly T independent as was previously pointed out12,21,23 and the low-energy conductivity can be written as
), which indicates relatively coherent charge dynamics. Hereafter, we call the narrow and broad Drude components the coherent and incoherent components (σD and σin), respectively. The incoherent component turned out to be nearly T independent as was previously pointed out12,21,23 and the low-energy conductivity can be written as

The evolution of each component with x for Co-Ba122 is shown in Figs. 2(b)–2(d)12. With Co doping, the weight of the narrow Drude component (coherent Drude weight) increases, whereas that of the broad Drude component shows no appreciable change. Figures 2(e)–2(h) show the evolution of the spectrum with P doping. The substitution of isovalent P for As supplies neither extra electrons nor holes. However, the coherent Drude weight remarkably increases with P doping without changing the total low-energy spectral weight below 6000 cm−1; the spectral weight is transferred to the coherent component from the higher-energy region10. As a result, the narrow Drude component dominates in the low-energy spectrum of BaFe2P2 [Fig. 2(h)].
The decomposition of the spectrum of KFe2As2 [Fig. 2(i)] is nearly the same as that of BaFe2As2, in which the fraction of the coherent Drude weight remains small, or even smaller and hence the low-energy conductivity spectrum is also dominated by the incoherent component. In view of the spectrum presented in Ref. 25 for the K content x = 0.4, the highly incoherent spectrum seems to persist over the entire doping range of K-Ba122 without showing any appreciable spectral change.
Discussion
Here, we discuss the resistivity and optical conductivity results for the three doped BaFe2As2 systems in the context of the available results for the Hall coefficient and the FS observed by ARPES. In the high-temperature PT phase of BaFe2As2, there are two electron FS pockets near the Brillouin zone boundary and three hole FS pockets around the zone center. Co doping makes the hole FS shrink and the electron FS expand5,6. The Hall coefficient, indeed, decreases in magnitude with a negative sign as doping proceeds18. Hence, the increase in the coherent Drude weight with Co doping is associated predominantly with the increase in electron carriers supplied by the dopant Co atoms and introduced electrons are not localised on the Co atom26.
On the other hand, the hole FS expands (the electron FS shrinks) with K doping and eventually the electron FS disappears in the highly doped region7,27. However, the resistivity does not decrease appreciably with K doping and the coherent Drude weight remains small over the entire doping range. These observations are in contrast to the electron-doped Co-Ba122 system. To reconcile these results with the doping evolution of the FS observed by ARPES, it is necessary to assume that quasiparticle states on a substantial part of the hole FS pockets remain incoherent in the hole-doped system.
The result for the isovalent P doping gives additional evidence for the electron–hole asymmetry. With P doping, the numbers of the electron and hole FS pockets do not change and thus the FS topology does not significantly change over the entire range of P content, although one of the hole FS pockets is more warped along the c-axis direction as x increases24. Nevertheless, the P doping significantly increases the coherent Drude weight and decreases the resistivity, which transforms the bad metallic BaFe2As2 into a good metal as in the case of Co doping. The coherent Drude weight is affected by the carrier density and the effective mass (the influence of the effective mass will be discussed later). In view of the negative Hall coefficient, the magnitude of which decreases with increasing P content3, it follows that, as doping proceeds, the coherent region in the momentum space, which is originally restricted to a portion of the electron FS pockets, gradually expands within the electron FS pockets, while the states on the hole FS pockets remain incoherent. This agrees with the conclusion drawn from the contrasting evolution of coherence/incoherence for electron- and hole-doped BaFe2As2. Earlier, it was reported that holes are subject to stronger scattering than electrons18,19,28. The result of P-Ba122 is reminiscent of the hole-doped high-Tc cuprates, in which an increase in the hole doping level from the underdoped to the optimally doped region makes the coherent states extend from the nodal to the antinodal region on the FS above the pseudogap temperature.
In Fig. 3(a), we plot the weight of the narrow Drude component ND as a function of the dopant concentration x for the three systems. ND is calculated with

where m0 and V are the free electron mass and the cell volume containing one Fe atom, respectively. ND is proportional to the coherent carrier density nD and inversely proportional to the carrier effective mass m*:  . Open symbols indicate the data compiled from Refs. 10, 12 and 25. Strikingly different evolutions of ND are seen, despite the similar phase diagram for each system. For Co-Ba122, an initial increase in ND with x is very steep. The ND of P-Ba122 shows a superlinear increase with x, a gradual increase followed by a rapid increase for x > 0.6. The much faster increase in ND with Co doping indicates that electron carriers are involved in the coherent charge dynamics. By contrast, the ND for K-Ba122 weakly decreases with increasing x. Compared with the doping evolution of resistivity shown in Fig. 1, it is clear that the magnitude of resistivity follows ND in the high-T region in each system. Note that, in the case of K doping, the resistivity only slightly decreases with x, but the hole density steadily increases with x, as evidenced by the increase in the volume of the hole FS observed by ARPES. The measurement of quantum oscillations for KFe2As2 revealed an enhancement in m*29,30, indicating that the decrease in ND is partly due to the increase in m*. Probably, the coherent hole carrier density nD would increase with a rate of increase slower than that of m*. Unlike the K doping, a decrease in m* with x (for x > 0.3) is reported for P doping by quantum oscillations31. m* decreases by a factor of 2–3 from x = 0.3 to 1. In this respect, the increase in ND for P-Ba122 may, in most part, be due to a decrease in m*.
. Open symbols indicate the data compiled from Refs. 10, 12 and 25. Strikingly different evolutions of ND are seen, despite the similar phase diagram for each system. For Co-Ba122, an initial increase in ND with x is very steep. The ND of P-Ba122 shows a superlinear increase with x, a gradual increase followed by a rapid increase for x > 0.6. The much faster increase in ND with Co doping indicates that electron carriers are involved in the coherent charge dynamics. By contrast, the ND for K-Ba122 weakly decreases with increasing x. Compared with the doping evolution of resistivity shown in Fig. 1, it is clear that the magnitude of resistivity follows ND in the high-T region in each system. Note that, in the case of K doping, the resistivity only slightly decreases with x, but the hole density steadily increases with x, as evidenced by the increase in the volume of the hole FS observed by ARPES. The measurement of quantum oscillations for KFe2As2 revealed an enhancement in m*29,30, indicating that the decrease in ND is partly due to the increase in m*. Probably, the coherent hole carrier density nD would increase with a rate of increase slower than that of m*. Unlike the K doping, a decrease in m* with x (for x > 0.3) is reported for P doping by quantum oscillations31. m* decreases by a factor of 2–3 from x = 0.3 to 1. In this respect, the increase in ND for P-Ba122 may, in most part, be due to a decrease in m*.
(a) Spectral weight of the narrow Drude component ND as a function of element substitution content x. Co-Ba122, P-Ba122 and K-Ba122 are indicated as blue, orange and red curves, respectively. Open symbols show the data from Refs. 10, 12 and 25. (b) ω = 0 value of the broad Drude component as a function of x. Open and closed symbols show the values obtained from the decomposition of the optical conductivity spectrum (Fig. 2) and from the analysis of the temperature dependence of resistivity, respectively.
A bad metallic behavior in the iron arsenides manifests in the high-T region, where the magnitude of resistivity is fairly high and the resistivity shows a tendency for saturation. This signals a dominant contribution of the broad (incoherent) Drude component at high temperatures in equation (1). σin is only weakly dependent on the temperature, which is found to reproduce the low-energy σ(T, ω) well12,23. The resistivity saturation is understood in terms of conductivity in two channels at ω = 0,

where σin is the ω = 0 value of the incoherent conductivity term. For iron arsenides, σin is comparable with σD. The resistivity from the coherent component is expressed by the sum of the contributions from T-independent elastic and T-dependent inelastic scattering (ρ0 and ρε, respectively);  . With increasing temperature, σD decreases and consequently the contribution of σin becomes dominant.
. With increasing temperature, σD decreases and consequently the contribution of σin becomes dominant.
Equation (2) happens to be similar to a simple parallel resistor formula empirically describing the resistivity saturation, in which σin is replaced by  , ρsat being the maximum resistivity corresponding to the carrier mean free path equal to the lattice spacing32:
, ρsat being the maximum resistivity corresponding to the carrier mean free path equal to the lattice spacing32:  . The present σin is not such a universal quantity but is dependent on the material and the doping level as shown in Fig. 3(b). This is distinct not only from the case of conventional resistivity saturating metals but also from the non-saturating resistivity of the known bad metals, many of which are in close proximity to a Mott insulating state, such as high-Tc cuprates33,34. The non-saturating resistivity is thought to arise from a reduction in low-frequency conductivity with increasing temperature, the spectral weight of which is transferred to higher frequencies involving transitions to the upper Hubbard band34,35. In iron arsenides, the presence of multiple carriers with distinct characteristics is responsible for the apparent resistivity saturation and the highly incoherent hole carriers with a mean free path shorter than the lattice spacing14 are mainly responsible for the bad metallic behavior.
. The present σin is not such a universal quantity but is dependent on the material and the doping level as shown in Fig. 3(b). This is distinct not only from the case of conventional resistivity saturating metals but also from the non-saturating resistivity of the known bad metals, many of which are in close proximity to a Mott insulating state, such as high-Tc cuprates33,34. The non-saturating resistivity is thought to arise from a reduction in low-frequency conductivity with increasing temperature, the spectral weight of which is transferred to higher frequencies involving transitions to the upper Hubbard band34,35. In iron arsenides, the presence of multiple carriers with distinct characteristics is responsible for the apparent resistivity saturation and the highly incoherent hole carriers with a mean free path shorter than the lattice spacing14 are mainly responsible for the bad metallic behavior.
The result shown in Fig. 3(a) demonstrates that doping controls ND in quite different ways depending on dopant sites and/or species. It is surprising that any of the different doping processes leads to the emergence of superconductivity. The critical doping level above which superconductivity appears more or less depends on the suppression rate of the AFO order, but it is an open question as to what conditions should be fulfilled for superconductivity to appear. On the other hand, the result indicates that the SC phase persists as long as ND is sufficiently small [ND < 0.02–0.03, shaded region in Fig. 3(a)] and that the system cannot sustain superconductivity when ND becomes larger or the charge dynamics becomes more coherent. ND rapidly increases with Co doping and soon reaches ~0.02 at x ~ 0.10. In the case of P doping, ND increases slowly and exceeds 0.03 at approximately x = 0.6. This seems to corroborate the fact that the SC phase terminates at x ~ 0.15 and ~ 0.7 for Co and P doping, respectively. Unlike these two systems, the ND of K-Ba122 maintains small values up to x = 1, consistent with the persistent superconductivity to KFe2As2. The incoherent normal-state charge dynamics is therefore a prerequisite for superconductivity.
Finally, we analyse the T dependence of the resistivity in the PT phase predominantly arising from the coherent component and search for a correlation with superconductivity. Assuming the two parallel (inelastic) scattering channels, we adopt a dual-component analysis for the T-dependent part of resistivity, ρε(T) = α1T + α2T2. The T2 term is typical of a conventional Fermi liquid and the T-linear term usually results from electron–boson interactions such as antiferromagnetic spin fluctuations. This dual-component analysis was applied to fit the resistivity of cuprates36 and iron pnictides37. However, this formula does not reproduce the trend for saturation observed for most iron arsenides at high temperatures. Therefore, we have to incorporate the incoherent channel σin explicitly and use the formula

where ρ0 represents the elastic scattering component adding to the inelastic scattering processes. σin can be estimated from the ω → 0 value of the broad (incoherent) Drude component in the present optical conductivity spectrum. For K-Ba122, larger values of σin are required to fit the resistivity curves than the experimentally extracted values. This might indicate that the decomposition of optical conductivity underestimates the contribution from the incoherent component, pointing towards the more incoherent charge dynamics inherent in K-Ba122 at high temperatures. Figure 4 shows the fitting results of the resistivity curves in the PT phase for the three systems under consideration. For undoped and underdoped compounds showing the AFO order, in-plane resistivity anisotropy is observed even in the PT phase above Ts, but the anisotropy is strongly suppressed by annealing16,38, which guarantees the present fitting down to near Ts. Equation (3) with σin reproduces well the resistivity curves over a wide temperature and doping range.
Figures 5(a)–5(c) show the doping dependences of the coefficients of the T-linear and square terms multiplied by ND, α1·ND and α2·ND, respectively, for the three doping systems obtained using the best-fit parameters, α1 and α2, to reproduce the resistivity curves (Fig. 4). For the compositions we did not measure the optical spectrum, ND is estimated by assuming smooth variation with x, shown as the dashed curves in Fig. 3(a). In the framework of the present two-fluid and dual-channel analysis, α1·ND and α2·ND are more directly related to the scattering rate of the coherent carriers 1/τD (σD = NDe2τD/m0). In common with the three systems, α1·ND is largest near the AFO-SC phase boundary where Tc is highest, whereas it becomes vanishingly small in the overdoped regime where superconductivity disappears in Co- and P-Ba122. Superconductivity in K-Ba122 persists up to x = 1, but α1·ND remarkably decreases on going from x = 0.69 to 0.88. This probably corresponds to the disappearance of the electron FS pockets7 and/or the change in the SC gap function on FS from a nodeless39 to a nodal one40,41. Unlike α1·ND, α2·ND remains finite over a wide range of doping regardless of the Tc value and does not show any noteworthy feature at the phase boundary. As shown in Fig. 3(a), the weight of the coherent Drude component ND varies monotonically with x. Therefore, the non-monotonic change in α1·ND certainly arises from that of α1, the T-linear channel of the carrier scattering rate.
Doping evolution of the coefficients of the T-linear and T2 components (α1·ND and α2·ND, respectively) for (a) Co-Ba122, (b) P-Ba122 and (c) K-Ba122 determined from the fitting shown in Fig. 4.
The T = 0 electronic phases are colour-coded: AFO in blue, SC in yellow, AFO-SC coexisting region in gradation and non-SC metallic in white. Lower panels show the electronic phase diagrams for each system.
The predominance of the T-linear term implies stronger inelastic scattering of carriers and the observed correlation between α1·ND and Tc strongly suggest that the scattering mechanism giving rise to the T-linear resistivity has an intimate connection with the SC-pair formation. Cooper et al. attempted to fit the temperature dependence of the in-plane resistivity of highly doped La2−xSrxCuO4 (x > 0.15) using a similar formula36. They found that α1 is largest at x = 0.19, which does not coincide with the composition showing the highest Tc and decreases with an increase or a decrease in the doping level, whereas α2 is only weakly dependent on the hole concentration down to x = 0.19. It should be noted that the T-linear resistivity in the hole-doped cuprates is different in nature. T-linearity in the cuprates persists up to very high temperatures, ~1000 K or even higher without showing resistivity saturation and originates from highly incoherent quasiparticle states. The quasiparticle scattering rate (1/τ) in the cuprates is strongly momentum (and frequency) dependent and is extremely high at momenta near the antinodes,  , which is near the so-called Planckian dissipation limit36,42. This is in contrast to the present iron pnictide case, in which the T-linear term arises from the coherent channel in parallel to the incoherent one and the resistivity exhibits a tendency for saturation due to the nearly T-independent incoherent term. The width of the narrow Drude component is ~200 cm−1 at T = 300 K for every system near the doping level that produces the highest Tc value. This corresponds to
, which is near the so-called Planckian dissipation limit36,42. This is in contrast to the present iron pnictide case, in which the T-linear term arises from the coherent channel in parallel to the incoherent one and the resistivity exhibits a tendency for saturation due to the nearly T-independent incoherent term. The width of the narrow Drude component is ~200 cm−1 at T = 300 K for every system near the doping level that produces the highest Tc value. This corresponds to  , which is by a factor of ~6 lower than that in La2–xSrxCuO4.
, which is by a factor of ~6 lower than that in La2–xSrxCuO4.
The T-linear resistivity is often invoked in relation to enhanced scattering from critical fluctuations near a quantum critical point (QCP). For P-Ba122, the presence of a magnetic QCP at x ~ 0.3 was suggested31,43. The T-linear resistivity coefficient α1 peaks at x ~ 0.3 and the effective mass m* estimated from de Haas oscillations increases from the overdoped region towards x ~ 0.3. Unfortunately, it is not clear whether the QCP scenario is applicable to Co and K doping because there have been no reports of the evolution of m* for Co- and K-Ba122. For every doped system, the SC phase is not confined to a region where α1 (or α1·ND) shows a peak and persists to x = 1 in the case of K-Ba122. Therefore, the present results support the scenario that superconductivity in the iron arsenides arises, irrespective of the presence or otherwise of a QCP, from strongly x-dependent coupling with some bosonic excitations, which is a source of the T-linear carrier scattering in the coherent component. For the incoherent component, the temperature dependence is very weak. This component experiences extremely strong scattering, which is presumably related to strong electronic correlations working orbital-selectively, already at low temperatures and additional scattering channels, such as electron–boson scattering, would be no more visible at elevated temperatures.
The facts that α1 and Tc attain large values near the AFO-SC phase boundary and that they steeply decrease farther away from the boundary suggest that the bosonic excitations originate from the fluctuations of the AFO order. As we discussed in the preceding study of the anomalous response of the AFO phase to dopant impurities38,44, the AFO phase is a unique spin-charge-orbital complex. Hence, inelastic scattering from short-range dynamical spin-charge-orbital correlations is a candidate of the T-linear resistivity and hence pairing interactions.
Methods
Single crystals of Co-, P- and K-doped BaFe2As2 were grown by the self-flux method12,45,46 and were post-annealed to improve the sample quality. Resistivity measurements were performed on the ab plane using the four-terminal method. Optical reflectivity was measured at T = 300 K with the incident light almost normal to the ab plane in the frequency range 50–40000 cm−1 using a Fourier transform infrared spectrometer (Bruker IFS113v) and a grating monochromator (JASCO CT-25C). The optical conductivity was derived from the Kramers–Kronig transformation of the reflectivity spectrum. The Hagen–Rubens or Drude–Lorentz formula was used for the low-energy extrapolation in order to smoothly connect to the spectrum in the measured region and to fit the measured resistivity value at ω = 0.
References
Rotter, M., Pangerl, M., Tegel, M. & Johrendt, D. Superconductivity and crystal structures of (Ba1–xKx)Fe2As2 (x = 0–1). Angew. Chem. Int. Ed. 47, 7949–7952 (2008).
Nandi, S. et al. Anomalous suppression of the orthorhombic lattice distortion in superconducting Ba(Fe1–xCox)2As2 single crystals. Phys. Rev. Lett. 104, 057006 (2010).
Kasahara, S. et al. Evolution from non-Fermi- to Fermi-liquid transport via isovalent doping in BaFe2(As1–xPx)2 superconductors. Phys. Rev. B 81, 184519 (2010).
Thaler, A. et al. Physical and magnetic properties of Ba(Fe1–xRux)2As2 single crystals. Phys. Rev. B 82, 014534 (2010).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nature Phys. 6, 419–423 (2010).
Ideta, S. et al. Carrier doping versus impurity potential effect in transition metal-substituted iron-based superconductors. Phys. Rev. Lett. 110, 107007 (2013).
Malaeb, W. et al. Abrupt change in the energy gap of superconducting Ba1–xKxFe2As2 single crystals with hole doping. Phys. Rev. B 86, 165117 (2012).
Miyake, T., Kosugi, T., Ishibashi, S. & Terakura, K. Electronic structure of novel superconductor Ca4Al2O6Fe2As2 . J. Phys. Soc. Jpn. 79, 123713 (2010).
Usui, H. & Kuroki, K. Maximizing the Fermi-surface multiplicity optimizes the superconducting state of iron pnictide compounds. Phys. Rev. B 84, 024505 (2011).
Nakajima, M. et al. Crossover from bad to good metal in BaFe2(As1–xPx)2 induced by isovalent P substitution. Phys. Rev. B 88, 094501 (2013).
Hu, W. Z. et al. Origin of the spin density wave instability in AFe2As2 (A = Ba, Sr) as revealed by optical spectroscopy. Phys. Rev. Lett. 101, 257005 (2008).
Nakajima, M. et al. Evolution of the optical spectrum with doping in Ba(Fe1–xCox)2As2 . Phys. Rev. B 81, 104528 (2010).
Hancock, J. N. et al. Strong coupling to magnetic fluctuations in the charge dynamics of iron-based superconductors. Phys. Rev. B 82, 014523 (2010).
Tu, J. J. et al. Optical properties of the iron arsenic superconductor BaFe1.85Co0.15As2 . Phys. Rev. B 82, 174509 (2010).
Barišić, N. et al. Electrodynamics of electron-doped iron pnictide superconductors: Normal-state properties. Phys. Rev. B 82, 054518 (2010).
Nakajima, M. et al. Unprecedented anisotropic metallic state in undoped iron arsenide BaFe2As2 revealed by optical spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 108, 12238–12242 (2011).
Ishida, S. et al. Manifestations of multiple-carrier charge transport in the magnetostructurally ordered phase of BaFe2As2 . Phys. Rev. B 84, 184514 (2011).
Rullier-Albenque, F., Colson, D., Forget, A. & Alloul, H. Hall effect and resistivity study of the magnetic transition, carrier content and Fermi-liquid behavior in Ba(Fe1–xCox)2As2 . Phys. Rev. Lett. 103, 057001 (2009).
Shen, B. et al. Transport properties and asymmetric scattering in Ba1–xKxFe2As2 single crystals. Phys. Rev. B 84, 184512 (2011).
Ohgushi, K. & Kiuchi, Y. Doping dependence of Hall coefficient and evolution of coherent electronic state in the normal state of the Fe-based superconductor Ba1–xKxFe2As2 . Phys. Rev. B 85, 064522 (2012).
Wu, D. et al. Optical investigations of the normal and superconducting states reveal two electronic subsystems in iron pnictides. Phys. Rev. B 81, 100512(R) (2010).
Lucarelli, A. et al. Charge dynamics of Co-doped BaFe2As2 . New J. Phys. 12, 073036 (2010).
Dai, Y. M. et al. Hidden T-linear scattering rate in Ba0.6K0.4Fe2As2 revealed by optical spectroscopy. Phys. Rev. Lett. 111, 117001 (2013).
Ye, Z. R. et al. Doping dependence of the electronic structure in phosphorus-doped ferropnictide superconductor BaFe2(As1–xPx)2 studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 86, 035136 (2012).
Li, G. et al. Probing the superconducting energy gap from infrared spectroscopy on a Ba0.6K0.4Fe2As2 single crystal with Tc = 37 K. Phys. Rev. Lett. 101, 107004 (2008).
Wadati, H., Elfimov, I. & Sawatzky, G. A. Where are the extra d electrons in transition-metal-substituted iron pnictides? Phys. Rev. Lett. 105, 157004 (2010).
Nakayama, K. et al. Universality of superconducting gaps in overdoped Ba0.3K0.7Fe2As2 observed by angle-resolved photoemission spectroscopy. Phys. Rev. B 83, 020501(R) (2011).
Muschler, B. et al. Band- and momentum-dependent electron dynamics in superconducting Ba(Fe1–xCox)2As2 as seen via electronic Raman scattering. Phys. Rev. B 80, 180510(R) (2009).
Terashima, T. et al. Fermi surface and mass enhancement in KFe2As2 from de Haas-van Alphen effect measurements. J. Phys. Soc. Jpn. 79, 053702 (2010).
Terashima, T. et al. Complete Fermi surface in BaFe2As2 observed via Shubnikov-de Haas oscillation measurements on detwinned single crystals. Phys. Rev. Lett. 107, 176402 (2011).
Shishido, H. et al. Evolution of the Fermi surface of BaFe2(As1–xPx)2 on entering the superconducting dome. Phys. Rev. Lett. 104, 057008 (2010).
Wiesmann, H. et al. Simple model for characterizing the electrical resistivity in A-15 superconductors. Phys. Rev. Lett. 38, 782 (1977).
Gunnarsson, O., Calandra, M. & Han, J. E. Colloquium: Saturation of electrical resistivity. Rev. Mod. Phys. 75, 1085–1099 (2003).
Hussey, N. E., Takenaka, K. & Takagi, H. Universality of the Mott-Ioffe-Regel limit in metals. Phil. Mag. 84, 2847–2864 (2004).
Deng, X. et al. How bad metals turn good: Spectroscopic signatures of resilient quasiparticles. Phys. Rev. Lett. 110, 086401 (2013).
Cooper, R. A. et al. Anomalous criticality in the electrical resistivity of La2–xSrxCuO4 . Science 323, 603–607 (2009).
Doiron-Leyraud, N. et al. Correlation between linear resistivity and Tc in the Bechgaard salts and the pnictide superconductor Ba(Fe1–xCox)2As2 . Phys. Rev. B 80, 214531 (2009).
Ishida, S. et al. Anisotropy of the in-plane resistivity of underdoped Ba(Fe1–xCox)2As2 superconductors induced by impurity scattering in the antiferromagnetic orthorhombic phase. Phys. Rev. Lett. 110, 207001 (2013).
Ding, H. et al. Observation of Fermi-surface-dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2 . Europhys. Lett. 83, 47001 (2008).
Fukazawa, H. et al. Possible multiple gap superconductivity with line nodes in heavily hole-doped superconductor KFe2As2 studied by 75As nuclear quadrupole resonance and specific heat. J. Phys. Soc. Jpn. 78, 083712 (2009).
Okazaki, K. et al. Octet-line node structure of superconducting order parameter in KFe2As2 . Science 337, 1314–1317 (2012).
Zaanen, J. Why the temperature is high. Nature 430, 512–513 (2004).
Hashimoto, K. et al. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1–xPx)2 . Science 336, 1554–1557 (2012).
Nakajima, M. et al. Effect of Co doping on the in-plane anisotropy in the optical spectrum of underdoped Ba(Fe1–xCox)2As2 . Phys. Rev. Lett. 109, 217003 (2012).
Nakajima, M. et al. Growth of BaFe2(As1–xPx)2 single crystals (0 ≤ x ≤ 1) by Ba2As3/Ba2P3-flux method. J. Phys. Soc. Jpn. 81, 104710 (2012).
Kihou, K. et al. Single crystal growth and characterization of the iron-based superconductor KFe2As2 synthesized by KAs flux method. J. Phys. Soc. Jpn. 79, 124713 (2010).
Acknowledgements
M.N. and S.I. thank the Japan Society for the Promotion of Science (JSPS) for the financial support. Discussions with T. Misawa, M. Imada and A. Fujimori were helpful in preparing this manuscript. This work was supported by the Japan-China-Korea A3 Foresight Program and Grant-in-Aid for JSPS Fellows from JSPS, Grant-in-Aid for Scientific Research from JSPS and the Ministry of Education, Culture, Sports, Science and Technology, Japan and the Strategic International Collaborative Research Program (SICORP) from Japan Science and Technology Agency.
Author information
Authors and Affiliations
Contributions
M.N. and T.T. conducted the optical spectroscopy measurements and analysed the data. M.N., K.K., T.S., C.H.L., H.F., Y.K. and A.I. synthesised the single crystals. M.N., S.I., Y.T., T.K. and T.I. carried out the resistivity measurements. H.E. and S.U. designed and coordinated the experiment. All authors contributed to and discussed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Nakajima, M., Ishida, S., Tanaka, T. et al. Normal-state charge dynamics in doped BaFe2As2: Roles of doping and necessary ingredients for superconductivity. Sci Rep 4, 5873 (2014). https://doi.org/10.1038/srep05873
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05873
This article is cited by
-
The breakdown of both strange metal and superconducting states at a pressure-induced quantum critical point in iron-pnictide superconductors
Nature Communications (2023)
-
Doping-dependent superconducting physical quantities of K-doped BaFe\(_2\)As\(_2\) obtained through infrared spectroscopy
Scientific Reports (2022)
-
Role of the orbital degree of freedom in iron-based superconductors
npj Quantum Materials (2017)
-
High-temperature superconductivity in iron pnictides and chalcogenides
Nature Reviews Materials (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.