Abstract
The mechanisms that underlie fascinating inter-individual interactions among animal groups have attracted increasing attention from biologists, physicists and system scientists. There are two well-known types of interaction patterns: hierarchical and egalitarian. In the former type, individuals follow their leaders, whereas they follow their neighbors in the latter. Using high-resolution spatiotemporal data derived from the free flights of a flock of pigeons, we show that pigeon flocks actually adopt a mode that switches between the two aforementioned strategies. To determine its flight direction, each pigeon tends to follow the average of its neighbors while moving along a smooth trajectory, whereas it switches to follow its leaders when sudden turns or zigzags occur. By contrast, when deciding how fast to fly, each pigeon synthesizes the average velocity of its neighbors. This switching mechanism is promising for possible industrial applications in multi-robot system coordination, unmanned vehicle formation control and other areas.
Similar content being viewed by others
Introduction
Over the last decade, scientists have been investigating common, possibly universal, features of the collective behaviors of animals, bacteria, cells, molecular motors and driven granular matter1. Biological social organisms form striking aggregation patterns, displaying cohesion, polarization and collective intelligence2. The most interesting characteristic of biological groups, such as bird flocks3,4, fish schools7,8,9, insect swarms10, bacterial colonies11 and metastasizing cancer cells12, is the emergence of ordered states where the agents move in the same direction13,14,15,16,17,18. The pursuit for an ordered state is also the focus of many closely related problems, such as consensus19, rendezvous20, synchronization21 and cooperation22. This type of distributed collective system has direct implications for sensor network data fusion23, load balancing24, unmanned air vehicles20, attitude alignment of satellite clusters25, multi-robot formation control26, human population behavior evolution analysis27, evacuation strategies for emergency escapes during panics28, etc.
Among the numerous examples of collective biological movement, many studies have attempted to understand the flocking of birds. For example, wild geese try to synchronize their velocities during migration to keep the rigidity of the V-shaped formation29, which can save the kinetic energy for the whole flock. As another paradigm of birds' collective phenomena, during landing procedure, it is shown by30 that birds arrive at a decision resulting in their synchronized position and velocity. Cavagna et al.31 obtained high resolution spatial data of thousands of starlings and detected a power-law decay in the behavioral correlation. Dell'Ariccia et al.32 found that the homing performance of a flock of birds flying was significantly better than that of the birds when they were released individually. Extensive studies have identified various features of bird flocks, including the initiation of movement and the mode of propagation33, anti-predatory positional effects on vigilance34,35, flock positional effects and intra-specific aggression in European starlings36 and three-dimensional congregation37.
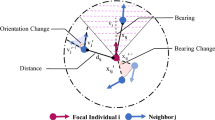
There are two well-known types of interaction pattern. The first is called the egalitarian pattern, where a representative model called the fixed neighborhood region (FNR) model, assumes a ball-shaped eyesight range with a fixed radius13,38, as shown in Figure 1a. A recent large-scale study of 2,600 individual starlings suggested another egalitarian pattern3, where each agent merely interacts with a fixed number of nearest neighbors, instead of individuals within a specific distance. This is known as the fixed number of neighbors (FNN) model and it is illustrated in Figure 1b. The FNN mechanism is supported by a theoretical model39 as well as empirical observations of mosquitofish schools40.
In addition to the pairwise leader-follower relationship7,8, Nagy et al.4 proposed a hierarchical leadership network (HLN) model where each pigeon follows its leaders and is followed by some other pigeons, as illustrated in Figure 1c. Earlier experiments by Biro et al.41 also support the existence of HLN among homing pigeon flocks. Very recently, Xu et al.5,6 improved the HLN model by introducing reciprocal relationships and distance-dependent attraction/repulsion interactions.
These two seemingly contradictory interaction patterns suggest a significant question: which pattern determines the real collective dynamics of pigeon flocks? In the present study, we extend the previous understanding of this system and demonstrate the existence of a switching mechanism, i.e., each pigeon synthesizes the velocities of its neighbors and adopts the average direction of its neighbors while moving along a smooth trajectory, whereas it switches to follow its leaders when sudden turns or zigzags occur.
Results
Quantitative inter-agent movement relationship analysis
We analyzed real GPS data recordings of the three-dimensional positions and velocities of 11 free flights by 10 pigeons. The trajectories and an HLN topology of a typical experiment (labeled as ff5 in Figure 5) are shown in Figures S1 and S2, respectively, of Supporting Information(SI) and more details of the data and experiments are presented in the Methods and Materials. In addition to the results presented in Figure 5 and Figure S7 of SI, all of the other experimental results were derived from experiment ff5. To evaluate the interaction mechanisms that control the collective motions of pigeon flocks, we quantified the synchronization intensity and rigidity of the overall flock using a direction synchronization error index ϕ and a velocity synchronization error index ψ, respectively (see Methods and Materials). There are no clear biological results to demonstrate that “birds exhibit maximal synchronization,” but previous studies assume the use of a synchronization intensity as an index for collective bird behavior analysis1,3,4,5,6, thus it was also employed in the present investigation. Moreover, we did not aim to propose a dynamic model to accurately estimate the overall trajectory of the pigeon flock, as shown in Figure S1 of SI. Indeed, the flock trajectory is too complex to be modeled precisely using machining learning methods. Instead, we aimed to extract the switching mechanism between two well-accepted inter-agent interaction patterns, i.e., hierarchical and egalitarian patterns, based on quantitative data analysis.
The direction synchronization error ϕi(a) and velocity synchronization error ψi (b) for pigeons B to L.
In (a), there is no clear difference between HLN-min and FNR/FNN except for pigeon G, in which case HLN-min evidently outperforms FNN/FNR. However, this is not the case in (b). Instead, the advantages of FNR/FNN compared with HLN are quite significant when considering the velocity modulus. In this case, the indices ϕi and ψi are the average values of ϕi(t) and ψi(t) for the entire temporal evolution period, respectively, such as  and
and  with T = 120s. The error bars indicate the standard deviations during the temporal evolution period. Note that pigeons A and M act as the highest and the second highest leaders of HLN, thus their movements are generally not influenced by those of others. Therefore, they have not been taken into consideration.
with T = 120s. The error bars indicate the standard deviations during the temporal evolution period. Note that pigeons A and M act as the highest and the second highest leaders of HLN, thus their movements are generally not influenced by those of others. Therefore, they have not been taken into consideration.
(a) Curvatures of the trajectories of pigeons A, M, D, H, G. A and M are leaders, thus they have sharper curvatures than those of D, H, G. Moreover, it can be seen that pigeon G generally has a larger curvature than D and H, thereby indicating that it experienced more sudden turns. Without any loss of generality, we select pigeons D and H because they are followers in different levels. More precisely, D is lower than G and H is lower than D, as shown in Figure S2 of SI. (b) Percentages of the sudden turn points larger than η0 for different pigeons. The aforementioned observation is supported by (b) because the sudden turns percentage is significantly higher for G than those for D and H, which also helps to explain why HLN outperforms FNR/FNN only for pigeon G.
Temporal evolution of the average direction modeling errors ϕ with FNR/FNN and HLN patterns.
Clearly, some HLN-dominating temporal segments match the local maxima of the average curvature curve η* quite well. This figure suggests that pigeons tend to follow the directions of their leaders, rather than their neighbors, when experiencing sudden turns.
(a) Probability density function showing the dominating probabilities of HLN and FNR. The peaks of the HLN and FNR curves are at η = 0.022 (1/m) (vertical dashed line) and 0.033 (1/m) (vertical solid line), respectively. These two peaks are the typical dominating curvatures of HLN and FNR. (b) The typical dominating curvatures of HLN and FNR in the 11 free flight datasets. The typical dominating curvatures of HLN are all much higher than those of FNR.
The two indices ϕi and ψi are shown in Figures 2a and 2b, respectively. In the HLN pattern, some pigeons have more than one direct leaders and the best matching leader takes the lowest synchronization errors  and
and  , which is referred as HLN-min. Analogously, the average value of the matching errors of all the leaders
, which is referred as HLN-min. Analogously, the average value of the matching errors of all the leaders  and
and  is denoted as HLN-avg. As shown in Figure 2a, there is no obvious difference between FNR/FNN and HLN-min except for pigeon G, where HLN outperforms FNR/FNN. For conciseness, we use the abbreviation HLN to denote HLN-min. However, as shown in Figure 2b, the advantages of FNR/FNN are significant compared with HLN when considering the velocity modulus. The effects of a different neighborhood radius r on FNR and a different neighborhood size n on FNN are respectively shown in Figure S3 of SI, which indicate the robustness of the observations.
is denoted as HLN-avg. As shown in Figure 2a, there is no obvious difference between FNR/FNN and HLN-min except for pigeon G, where HLN outperforms FNR/FNN. For conciseness, we use the abbreviation HLN to denote HLN-min. However, as shown in Figure 2b, the advantages of FNR/FNN are significant compared with HLN when considering the velocity modulus. The effects of a different neighborhood radius r on FNR and a different neighborhood size n on FNN are respectively shown in Figure S3 of SI, which indicate the robustness of the observations.
Extraction of factors
Figure 3a shows the curvature η (see Materials and Methods for the definition of the curvature) of the trajectories for some of the pigeons in Figure S1 of SI. We define sudden turns as those with a curvature greater than a threshold η0. Figure 3b shows the percentage of sudden turns among all pigeons for η0 = 0.09, 0.10, 0.11 and 0.12 (1/m) (all points with η > 0.09 (1/m) are marked in Figure S1). Pigeon G always exhibited more sudden turns or zigzags than the other pigeons, except the two leaders A and M. Thus, we suggest that when facing sudden turns, a pigeon may not have sufficient time to synthesize its direction with its neighbors, so it will follow its direct leaders instead. This is why HLN outperforms FNR/FNN for pigeon G. By contrast, a pigeon tends to adopt the average direction of its neighbors when moving along a smooth trajectory. However, each pigeon should consider the velocities of its neighbors to determine its flight speed, otherwise it will be too far in front or lag behind the rest of the flock. Figure 2b suggests that FNR/FNN performs better in maintaining the rigidity of pigeon flocks.
Figure 4 shows the change in the average direction modeling error,  , with time. Sometimes the HLN exhibits significant advantages in modeling precision (i.e., lower synchronization errors). We compare HLN-dominating segments with the temporal evolutions of the average curvature,
, with time. Sometimes the HLN exhibits significant advantages in modeling precision (i.e., lower synchronization errors). We compare HLN-dominating segments with the temporal evolutions of the average curvature,  , for all eight followers. Indeed, there are 37 local minima of the HLN curve and 22 local maxima of the η-curve, where 12 segments agree well, which are defined as
, for all eight followers. Indeed, there are 37 local minima of the HLN curve and 22 local maxima of the η-curve, where 12 segments agree well, which are defined as  with threshold δ = 0.4s and i is the sequential number of the matching segments. Thereby, it is implied that pigeons tend to follow the directions of their leaders instead of their neighbors when experiencing sudden turns. To test the generality of this observation, Figure S4 of SI also shows the temporal curvature evolutions ηA, ηM, ηG, ηD of the two leaders A, M and the two followers G and D at different hierarchical levels. Again, some HLN-dominating segments match the peaks of the four curvature curves well, thereby supporting our conclusion.
with threshold δ = 0.4s and i is the sequential number of the matching segments. Thereby, it is implied that pigeons tend to follow the directions of their leaders instead of their neighbors when experiencing sudden turns. To test the generality of this observation, Figure S4 of SI also shows the temporal curvature evolutions ηA, ηM, ηG, ηD of the two leaders A, M and the two followers G and D at different hierarchical levels. Again, some HLN-dominating segments match the peaks of the four curvature curves well, thereby supporting our conclusion.
With respect to the temporal evolution of the velocity error index ψ (see Figure S5 of SI), there is no clear correlation between the HIN-dominating segments and the peaks of the curvature curve. By contrast, FNN/FNR generally has lower synchronization errors, which shows that the egalitarian pattern can describe the change in velocity better. We also show the temporal evolution of the modeling errors ϕ and ψ with different parameters for FNR/FNN patterns in Figure S6 of SI. Moderate changes in the parameters do not affect the main results.
Figure 5 shows the probability density functions for the HLN-dominating and FNR-dominating cases, respectively. The dotted curve (i.e., the highest curve) in Figure 5a is the curvature distribution. Given a curvature (e.g., η = 0.05 (1/m)), a probability of 1.8% indicates that 1.8% of the data points have a curvature of 0.05. If 60% of these data points with η = 0.05, HLN performs better than FNR, whereas the reverse is true for the other 40%. Thus, the HLN-dominating probability is 1.08% and the FNR-dominating probability is 0.72%. Note that due to the discretization resolution of η, in our numerical analysis, η = 0.05 means that η ∈ (0.05 − σ, 0.05 + σ] with a resolution of σ = 0.005. The peaks of the HLN-dominating and FNR-dominating density functions are emphasized by a solid vertical line and a dashed vertical line, respectively. These two values are the typical dominating curvatures for HLN and FNR, respectively. Figure 5 shows two statistical features: (i) the typical dominating curvature of HLN is larger than that of FNR; (ii) FNR typically works better for small-curvature cases whereas HLN performs better for large-curvature cases. These two features are also verified by the frequency maps for all 11 free flights, which are shown in Figure S7 of SI. Moreover, Figure 5 shows that HLN dominates some time instants, but also some time segments that correspond to large trajectory curvatures, which are highlighted by diamonds in Figure S1 of SI.
Theoretical model
We use a theoretical flocking model with a leader A and m followers  to further verify our results. Initially, as shown in Figure 6a, their positions pi = [xi, yi]T, (
to further verify our results. Initially, as shown in Figure 6a, their positions pi = [xi, yi]T, ( ) are distributed evenly as
) are distributed evenly as  and their initial movement directions are all upward as θi = π/2. The leader A moves along some predetermined ellipsoidal trajectories with decreasing curvatures at the upper peaks and the angular velocity of A, ω, is a constant that is not influenced by others. All of the followers adopt either FNR or HLN rules and they move in an L × L square with a periodical boundary condition. According to the FNR rules, each follower's movement direction is determined by the average direction of the instantaneous neighbors in a sphere with a radius r that has this follower at its center and its speed is set to the same as that of A so all individuals have the same speed at the same time. This type of alignment mechanism represents the interaction process of FNR well and FNN operates in a similar manner. For HLN, we arrange the individuals in a sequence as
and their initial movement directions are all upward as θi = π/2. The leader A moves along some predetermined ellipsoidal trajectories with decreasing curvatures at the upper peaks and the angular velocity of A, ω, is a constant that is not influenced by others. All of the followers adopt either FNR or HLN rules and they move in an L × L square with a periodical boundary condition. According to the FNR rules, each follower's movement direction is determined by the average direction of the instantaneous neighbors in a sphere with a radius r that has this follower at its center and its speed is set to the same as that of A so all individuals have the same speed at the same time. This type of alignment mechanism represents the interaction process of FNR well and FNN operates in a similar manner. For HLN, we arrange the individuals in a sequence as  and set an interaction topology as
and set an interaction topology as  , where the former is the direct leader of the latter. To focus on the sequential nature of the hierarchical effects, we ignore the movement direction mismatches between each leader-follower pair. Thus, with a time delay τ, the movement directions are iterated as
, where the former is the direct leader of the latter. To focus on the sequential nature of the hierarchical effects, we ignore the movement direction mismatches between each leader-follower pair. Thus, with a time delay τ, the movement directions are iterated as  .
.
(a) Illustration of the theoretical model where the leader A moves along smoother trajectories as the sizes of the ellipsoids increase. The hierarchical leadership network is  . Moreover, due to the periodical boundary condition, no agent other than the leader A can completely escape the influence of others. (b), (c) The synchronization index Ja of HLN and FNR increases with the trajectory curvature η. The parameters were set as: (b) L = 2.2, r = 1.3, m = 2, d = 0.7 and ω = π/50; (c) L = 2.2, r = 0.9, m = 6, d = 0.4 and ω = π/200. The initial speed was set to 0.03L and we tested different time delays. In this model, FNN is equivalent to FNR, e.g., FNR with r = 0.9 is equal to FNN with n = 4 and FNR with r = 1.3 is equal to FNN with n = 1. Each point is the average of 200 samples around the ellipse peak. According to the synchronization index Ja, HLN outperforms FNR for large curvatures beyond a specified threshold ηc, as indicated by the vertical lines in (b) and (c). Note that the displacements in (a) do not have a unit, thus the curvatures in (b) and (c) also have no unit.
. Moreover, due to the periodical boundary condition, no agent other than the leader A can completely escape the influence of others. (b), (c) The synchronization index Ja of HLN and FNR increases with the trajectory curvature η. The parameters were set as: (b) L = 2.2, r = 1.3, m = 2, d = 0.7 and ω = π/50; (c) L = 2.2, r = 0.9, m = 6, d = 0.4 and ω = π/200. The initial speed was set to 0.03L and we tested different time delays. In this model, FNN is equivalent to FNR, e.g., FNR with r = 0.9 is equal to FNN with n = 4 and FNR with r = 1.3 is equal to FNN with n = 1. Each point is the average of 200 samples around the ellipse peak. According to the synchronization index Ja, HLN outperforms FNR for large curvatures beyond a specified threshold ηc, as indicated by the vertical lines in (b) and (c). Note that the displacements in (a) do not have a unit, thus the curvatures in (b) and (c) also have no unit.
Figures 6b and 6c show that, depending on the synchronization index Ja (see Materials and Methods, the higher the better), HLN outperforms FNR for large curvatures beyond a specified threshold ηc, which is related to the time delay τ. In brief, the theoretical model again supports our conclusion that HLN is more likely to be adopted upon sudden turns, whereas FNR/FNN is applied in smooth conditions.
Discussion
Inter-individual interactions in collective biological groups are considered to involve two well-known mechanisms: following leaders or following neighbors. In the former mechanism, leadership can be hierarchical4 or mono-level12,27, whereas the neighbor-hood can be defined by geometry13,38 or topology3 in the latter. The controversy between the leadership-dominating and egalitarian strategies has lasted for years and it can be further generalized to monarchical and democratic ruling systems in socialized animal groups42. In the present study, we propose a more sophisticated system where pigeons switch between the two aforementioned strategies to facilitate the fine regulation of their movements in a variable environment. Each pigeon employs a hybrid strategy when deciding the direction of movement: it follows the leaders during sudden turns but synthesizes its neighbors movements when the trajectory is smooth. To determine its speed of flight, each pigeon also synthesizes its instantaneous neighbors to avoid potential lagging. To some extent, this is similar to how group decisions are made in other animal groups43. In addition, a pigeon flock is a sophisticated self-organized system, which could inspire the design of multi-agent systems. For example, the switchable hybrid strategy may improve the performance of multi-robot system coordination, particularly by reducing communication costs because HLN generally requires the transmission of much less information compared with FNR/FNN.
The present study only considers small pigeon flocks, thus these results still require further verification using real experimental data for other animal groups (e.g., starlings3,31, surf scoters2, wild geese29, insect colonies10 and fish schools9). Cross-species comparisons will determine the universality of the conclusions presented in this study, i.e., does this general switching mechanism underlie the behavior of many disparate animal flocks or is it only applicable to bird flocks (possibly even pigeons)? Another open question that requires further investigation is whether this switchable interaction mechanism operates in large-scale pigeon flocks and, if this is the case, how pigeons organize a large-scale hierarchical leadership network and whether the leader-follower relationships depend on the actual distance.
Methods
Data acquisition and description
Ten pigeons aged 1–5 years were used in the experiments conducted by Nagy et al.4. These experiments were permitted and supported by the Hungarian Racing Pigeon Sports Federation4. All of the birds had previous homing experience and most had competed previously in races (100 km) for young pigeons. The pigeons were normally allowed to fly freely outside the loft twice each day. Initially, each pigeon was equipped with a Plasticine dummy weight (16 g, i.e., the same size and weight as the GPS logger), which was fixed to their back with an elastic harness, so it could become habituated to flying and living with a load. The distance between the starting and ending point of the free flight was 14.8 km. The data analyzed comprised 11 free flights around the home loft. An average flight comprised 12 min in the air. In total, the GPS devices logged 32 h of flight time with 580,000 data points, each of which comprised x–, y– and z–coordinates based on the flat earth model4 with a temporal resolution of 0.2 s.
Quantification of movement synchronization
To quantify the direction synchronization performance of an arbitrary individual i with FNR/FNN, we define the synchronization indices as  and
and  . In this case, t is time variable,
. In this case, t is time variable,  is the set of neighbors of i where
is the set of neighbors of i where  is the number of neighbors, the movement angle
is the number of neighbors, the movement angle  and the symbol “.” denotes “inner product.” Hence,
and the symbol “.” denotes “inner product.” Hence,  represents the difference between the direction of individuals i and its neighbor j (i.e., smaller is better). Specifically,
represents the difference between the direction of individuals i and its neighbor j (i.e., smaller is better). Specifically,  and 2 for a completely synchronized couple and for a couple with opposite movements, respectively.
and 2 for a completely synchronized couple and for a couple with opposite movements, respectively.  and
and  denote the average and minimal values, respectively, of the differences in the movement directions between individual i and all its neighbors.
denote the average and minimal values, respectively, of the differences in the movement directions between individual i and all its neighbors.
Analogously, we define the velocity synchronization error indices as  and
and  . Clearly, if the velocity of i is perfectly synchronized with that of its neighbors, then ψij = 0. By contrast, if the velocities of i and its neighbors are very different, then ψij will be a large positive number. Similar to the notations of the direction synchronization indices,
. Clearly, if the velocity of i is perfectly synchronized with that of its neighbors, then ψij = 0. By contrast, if the velocities of i and its neighbors are very different, then ψij will be a large positive number. Similar to the notations of the direction synchronization indices,  and
and  denote the average and minimal values, respectively, of the velocity differences between individual i and all its neighbors.
denote the average and minimal values, respectively, of the velocity differences between individual i and all its neighbors.
In the same manner, we define the direction and velocity synchronization indices of HLN as  ,
,  ,
,  ,
,  . In this case,
. In this case,  denotes all the leaders of i and τij is the time delay between individual i and its leader j.
denotes all the leaders of i and τij is the time delay between individual i and its leader j.
The average velocity synchronization index is defined as  . We use this index rather than the order parameter in13 because the velocity modulus varies throughout the time evolution. Clearly, Ja = 1 implies complete velocity synchronization, whereas Ja = 0 represents a totally disordered state.
. We use this index rather than the order parameter in13 because the velocity modulus varies throughout the time evolution. Clearly, Ja = 1 implies complete velocity synchronization, whereas Ja = 0 represents a totally disordered state.
Trajectory curvature definition
The sudden turns and smooth points of the moving trajectories are differentiated quantitatively based on the curvature44:

where xi(t) and yi(t) are the xi– and yi–axis positions during the temporal evolution of pigeon i, respectively,  and
and  . Clearly, different points along the trajectory have different curvatures and a larger curvature indicates a higher likelihood that the corresponding point is part of a sudden turn. Note that the unit of pigeon displacements is m (meter), thus the curvature unit is 1/m in the present study.
. Clearly, different points along the trajectory have different curvatures and a larger curvature indicates a higher likelihood that the corresponding point is part of a sudden turn. Note that the unit of pigeon displacements is m (meter), thus the curvature unit is 1/m in the present study.
References
Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).
Lukeman, R. & Li, Y. X. Edelstein-Keshet L. Inferring individual rules from collective behavior. Proc. Natl. Acad. Sci. U.S.A. 107, 12576–12580 (2010).
Ballerini, M. et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Natl. Acad. Sci. U.S.A. 105, 1232–1237 (2008).
Nagy, M., Ákos, Z., Biro, D. & Vicsek, T. Hierachical group dynamics in pigeon flocks. Nature 464, 890–893 (2010).
Xu, X. K., Kattas, G. D. & Small, M. Reciprocal relationships in collective flights of homing pigeons. Phys. Rev. E 85, 026120 (2012).
Kattas, G. D., Xu, X. K. & Small, M. Dynamical modeling of collective behavior from pigeon flight data: flock cohesion and dispersion. PLoS. Comput. Biol. 8, e1002449 (2012).
Partridge, B. L. Effects of school size on the structure and dynamics of minnow schools. Anim. Behav. 28, 68–77 (1980).
Partridge, B. L., Pitcher, T., Cullen, J. M. & Wilson, J. The three-dimensional structure of fish schools. Behav. Ecol. Sociobiol. 6, 277–288 (1980).
Katz, Y., Tunstrom, K., Loannou, C. C., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. U.S.A. 108, 18720–18725 (2011).
Buhl, J. et al. From disorder to order in marching locusts. Science 312, 139–142 (2006).
Budrene, E. O. & Berg, H. Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature 376, 49–53 (1995).
Deisboeck, T. S. & Couzin, I. D. Collective behavior in cancer cell populations. BioEssays 31, 190–197 (2009).
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
D'Orsogna, M. R., Chuang, Y. L., Bertozzi, A. L. & Chayes, L. S. Self-propelled particles with soft-core interactions: patterns, stability and collapse. Phys. Rev. Lett. 96, 104302 (2006).
Chaté, H., Ginelli, F. & Montagne, R. Simple model for active nematics: quasi-long- range order and giant fluctuations. Phys. Rev. Lett. 96, 180602 (2006).
Hernandez-Ortiz, J. P., Stoltz, C. G. & Graham, M. D. Transport and collective dynamics in suspensions of confined swimming particles. Phys. Rev. Lett. 95, 204501 (2005).
Grégoire, G. & Chaté, H. Onset of collective and cohesive motion. Phys. Rev. Lett. 92, 025702 (2004).
Aldana, M., Dossetti, V., Huepe, C., Kenkre, V. M. & Larralde, H. Phase transitions in systems of self-propelled agents and related network models. Phys. Rev. Lett. 98, 095702 (2007).
Olfati-Saber, R. & Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Automat. Contr. 49, 1520–1533 (2004).
Martinez, S., Cortes, J. & Bullo, F. Motion coordination with distributed information. IEEE Contr. Syst. Mag. 27, 75–88 (2007).
Arenasa, A., Díaz-Guilerac, A., Kurths, J., Morenob, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep. 469, 93–153 (2008).
Guttal, V. & Couzin, I. D. Social interactions, information use and the evolution of collective migration. Proc. Natl. Acad. Sci. U.S.A. 107, 16172–16177 (2010).
Akyildiz, I. F., Su, W., Sankarasubramaniam, Y. & Cayirci, E. Wireless sensor networks: a survey. Comput. Netw. 38, 393–422 (2002).
Ogren, P., Fiorelli, E. & Leonard, N. E. Cooperative control of mobile sensor networks: adaptive gradient climbing in a distributed environment. IEEE Trans. Automat. Contr. 49, 1292–1302 (2004).
Arai, T., Pagello, E. & Parker, L. E. Guest editorial advances in multirobot systems. IEEE Trans. Robot. Autom. 18, 655–661 (2002).
Jadbabaie, A., Lin, J. & Morse, A. S. Coordination of groups of mobile agents using nearest neighbor rules. IEEE Trans. Automat. Contr. 48, 988–1001 (2003).
Torney, C. J., Levin, S. A. & Couzin, I. D. Specialization and evolutionary branching within migratory populations. Proc. Natl. Acad. Sci. U.S.A. 107, 20394–20399 (2010).
Helbing, D., Farkas, I. & Vicsek, T. Simulating dynamical features of escape panic. Nature 407, 487–490 (2000).
Portugal, S. J., Hubel, T. Y., Fritz, J., Heese, S., Trobe, D., Voelkl, D., Hailes, S., Wilson, A. M. & Usherwood, J. R. Upwash exploitation and downwash avoidance by flap phasing in ibis formation flight. Nature 505, 399–402 (2014).
Bhattacharya, K. & Vicsek, T. Collective decision making in cohesive flocks. New J. Phys. 12, 093019 (2010).
Cavagna, A. et al. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. U.S.A. 107, 11865–11870 (2010).
Dell'Ariccia, G., Dell'Omo, G., Wolfer, D. P. & Lipp, H. P. Flock flying improves pigeons' homing: GPS-track analysis of individual flyers versus small groups. Anim. Behav. 76, 1165–1172 (2008).
Potts, W. K. The chorus-line hypothesis of coordination in avian flocks. Nature 24, 344–345 (1984).
Elgar, M. A. Predator vigilance and group size in mammals and birds: a critical review of the evidence. Biol. Rev. 64, 13–33 (1989).
Beauchamp, G. Group-size effects on vigilance: a search for mechanisms. Behav. Process. 63, 111–121 (2003).
Keys, G. C. & Dugatkin, L. A. Flock size and position effects on vigilance, aggression and prey capture in the European starling. Condor 92, 151–159 (1990).
Parrish, J. K. & Hamner, W. H. Animal groups in three dimensions: how species aggregates (Cambridge University Press, Cambridge, 1997).
Couzin, I. D., Krause, J., James, R., Ruxton, G. D. & Franks, N. R. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11 (2002).
Bode, N. W. F., Franks, D. W. & Wood, A. J. Limited interactions in flocks: relating model simulations to empirical data. J. R. Soc. Interface 8, 301–304 (2011).
Herbert-Read, J. E., Perna, A., Mann, R. P., Schaert, T. M., Sumpter, D. J. T. & Ward, A. J. W. Inferring the rules of interaction of shoaling fish. Proc. Natl. Acad. Sci. U.S.A. 108, 18726–18731 (2011).
Biro, D., Sumpter, D., Meade, J. & Guilford, T. From compromise to leadership in pigeons homing. Curr. Biol. 16, 2123–2128 (2006).
Conradt, L. & Roper, T. J. Group decision-making in animals. Nature 421, 155–158 (2003).
Couzin, I. D., Krause, J., Franks, N. R. & Levin, S. A. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516 (2005).
Greub, W. H., Halperin, S. & Vanstone, R. Connections, curvature and cohomology (Academic Press INC, New York, 1972).
Acknowledgements
This research was supported partially by the National Natural Science Foundation of China under Grant Nos. 61322304, 51121002, 51120155001 and 11222543, the Program for New Century Excellent Talents in University under Grant No. NCET-11-0070 and the National Basic Research Program of China (973 Program) under Grant No. 2011CB013005. The authors acknowledge M. Nagy for providing and discussing the data.
Author information
Authors and Affiliations
Contributions
H.-T.Z., Z.S., T.V. and T.Z. wrote the main manuscript and designed the experiments; Z.S., L.S., G.F. and R.S. performed the experiments; H.-T.Z., G.F. and L.S. designed the data evaluation; H.-T.Z. and Z.C. performed the analysis and the data visualization. All of the authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supporting Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Zhang, HT., Chen, Z., Vicsek, T. et al. Route-dependent switch between hierarchical and egalitarian strategies in pigeon flocks. Sci Rep 4, 5805 (2014). https://doi.org/10.1038/srep05805
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05805
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.