Abstract
Gas hydrates are systems of prime importance. In particular, hydrogen hydrates are potential materials of icy satellites and comets and may be used for hydrogen storage. We explore the H2O–H2 system at pressures in the range 0–100 GPa with ab initio variable-composition evolutionary simulations. According to our calculation and previous experiments, the H2O–H2 system undergoes a series of transformations with pressure and adopts the known open-network clathrate structures (sII, C0), dense “filled ice” structures (C1, C2) and two novel hydrate phases. One of these is based on the hexagonal ice framework and has the same H2O:H2 ratio (2:1) as the C0 phase at low pressures and similar enthalpy (we name this phase Ih-C0). The other newly predicted hydrate phase has a 1:2 H2O:H2 ratio and structure based on cubic ice. This phase (which we name C3) is predicted to be thermodynamically stable above 38 GPa when including van der Waals interactions and zero-point vibrational energy and explains previously mysterious experimental X-ray diffraction and Raman measurements. This is the hydrogen-richest hydrate and this phase has a remarkable gravimetric density (18 wt.%) of easily extractable hydrogen.
Similar content being viewed by others
Introduction
Molecular compounds (cocrystals) of water ice (H2O) and hydrogen (H2) are known to form clathrate structures with hydrogen molecules encapsulated as guests in the host sublattice formed by water molecules. Hydrogen hydrates, as environmentally clean and efficient hydrogen storage materials, have excited significant interest. Extensive literature exists from both experimental1,2,3,4,5,6,7,8,9,10,11,12 and theoretical13,14 sides. Aside from the H2 molecules, many other small molecules can be encapsulated as guests in clathrates at elevated pressure (e.g., noble gases, nitrogen, oxygen, methane, chlorine). (See Ref. [15] and references therein) Hydrogen hydrates are important as potentially major materials of icy satellites and comets and hydrogen storage materials.
Twenty years after the first report of the formation of two filled-ice hydrogen hydrates by Vos et al.1, four hydrogen hydrate forms are known to exist at elevated pressures. Two of the hydrogen hydrates are clathrates, denoted as clathrate structure II (sII)3,5 and compound 0 (C0)12, the other two are filled ice hydrates, compound 1 (C1) and compound 2 (C2)1,2. The sII clathrate hydrate was synthesized under pressures of 180 to 220 MPa at 300 K and its structure was shown to contain 48 hydrogen molecules and 136 water molecules in the unit cell3. The C0 clathrate was recently found to be stable near 0.5 GPa and to have the composition 2H2O:1H2 and a trigonal quartz-like structure12. The water molecules in the C0 structure are arranged in a totally new way, different from the known ices or ice sublattices in hydrates structures. This structure has space group P3221, but this could possibly go as low as P32, depending on how the hydrogens are arranged12.
At higher pressures, clathrates give way to denser structures of the filled ice type. The C1 and C2 phases are formed at 0.36–0.9 GPa and ~2.4 GPa, respectively1,2,11. The C1 hydrate has a water host framework based on ice-II and a 6:1 water to hydrogen ratio. C2 has a 1:1 ratio of water to hydrogen and is composed of water molecules in the “cubic ice” (ice-Ic) framework and rotationally disordered hydrogen molecules15. Recent experiments7,8,9,10 indicate that the C2 hydrate undergoes a structural transformation from cubic to tetragonal phase at around 10–20 GPa, with an increasing difference in the unit cell axes and then transforms to another high-pressure phase near ~45 GPa. This high-pressure phase is maintained up to at least 80 GPa but its structure is not fully resolved. Given the difficulties in characterization of the chemical composition and crystal structure of these hydrates and believing that new phases are likely to exist, we decided to perform a computational search to revisit the H2O–H2 system under pressure.
Results
Using the evolutionary algorithm USPEX16,17,18,19,20, we explored all possible stable phases in the H2O–H2 system (See Methods). Remarkably, we have found two novel filled ice hydrogen hydrates and all known hydrogen hydrates (except the sII structure, because of the very large number of molecules in its unit cell). Thus, at pressures in the range 0–2 GPa, the sII structure was input separately in order to calculate stability ranges of phases in the H2O-H2 system. Fig. 1 shows the convex hull diagram for the H2O-H2 system.
Convex hull diagram for H2O-H2 system at selected pressures and zero temperature.
This figure shows the enthalpy of formation (in eV/molecule) of molecular compounds from pure H2O ice and H2. The red and yellow circles represent the C0 and Ih-C0 phases, respectively. The green star represents the sII structure.
With including the van der Waals (vdW) dispersion forces (See Methods), our results are generally in very good agreement with experiments, but with several novel aspects. At 0 GPa, the C0, C1 and a novel hydrogen hydrate phase are found stable or nearly stable in the H2O–H2 system, while the sII phase is metastable (~0.013 eV/molecule less stable than the mixture of stable compounds C0 and C1). The structure of the novel hydrogen hydrate is based on the framework of hexagonal ice (ice-Ih), with two hydrogen molecules hosted inside channels running along the hexagonal axis (Fig. 2a). It has a 2:1 ratio of water to hydrogen, same as C0 and space group Cc. We name it Ih-C0 to distinguish from C0. The enthalpy of the Ih-C0 phase is close to C0 and is slightly lower at pressures above ~0.4 GPa (Fig. S2 in Supplementary Information). At 1.5 GPa, in addition to the C0, Ih-C0 and C1 phases, the hydrate phase C2 with an ice-Ic framework structure becomes stable.
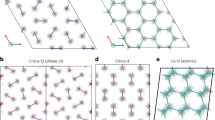
Crystal structures of Ih-C0 and C3 phases, cage structures in C2 and C3 phases.
(a) Ih-C0 structure at 0.5 GPa, (b) C3 structure at 30 GPa, (c) cages formed by water molecules in C3 at 100 GPa, the hydrogen molecules are located at the center of each chair-like H-O ring, (d) cages in “filled ice-Ic” C2, hydrogen molecules are in the center of the cage. Large red and small blue spheres are O and H atoms in water molecules, respectively; the yellow spheres represent the H2 molecules in (a) and (b) and represent H atoms in (c) and (d). Red dashed lines represent hydrogen bonds.
At pressures above 2 GPa, the C0 and Ih-C0 phases are calculated to be above the convex hull, indicating that these phases become unstable against decomposition into C1 and C2. Above 3.5 GPa, the C1 phase will also become unstable and the C2 phase will remain the only stable hydrate. For hydrate C2, USPEX calculations uncovered at least four typical energetically favorable candidate structures at different pressures, P41212, I41/amd, Pna21 and I41md (Fig. S3. in Supplementary Information). These structures differ in the orientations of water and hydrogen molecules, which is similar to Ref. [15]. The C2 phase will lose stability at ~14 GPa, which is much lower than 40 GPa suggested in the previous study7,10. We explain this by metastable persistence of C2 up to the pressure of 40 GPa. Between 14–28 GPa, there are, unexpectedly, no thermodynamically stable hydrates.
Near 30 GPa, another novel H2O–H2 phase is found to be stable at zero temperature. It has a 1:2 water to hydrogen ratio and net composition H6O. This novel hydrogen hydrate, which we name C3, has the highest hydrogen concentration among all hydrogen hydrates. If it can be synthesized at low pressures, it would be an attractive hydrogen storage material, having 18 wt.% concentration of easily separable (non-water) hydrogen. The C3 structure has space group P41 and is also based on the framework of ice-Ic (Fig. 2b), similar to low-pressure hydrate C2. The unit cell of C3 contains four water molecules, the H2 molecules are located at the center of chair-like H-O rings (formed by six oxygen and six hydrogen atoms) that form faces of the cage, as shown in Fig. 2c. Differently, in the C2 hydrate, the H2 molecules are in the center of the water cages (Fig. 2d). According to our calcualtions, the C3 phase will remain stable up to at least 120 GPa.
Our theoretical calculations indicate that the H2O–H2 system contains several stable phases, including open-network clathrate structures (C0) and dense filled ice phases (Ih-C0, C1, C2 and C3). The C0 phase is predicted to be stable at pressures below 1.5 GPa, which is close to the experimental result (below 0.8 GPa12). The C1 phase is predicted to be stable at pressures below 3.5 GPa, also close to the experimentally determined transition pressure of 2.5 GPa1. The zero-point vibration energy (ZPE) significantly affects the relative stability of hydrogen-rich structures21. We have estimated the ZPE within the quasi-harmonic approximation22 to refine the stability ranges of C2 and C3 phases above 10 GPa. When considering the ZPE, the stability field of the C2 phase expands up to ~19 GPa, but this phase remains dynamically stable and thus can exist as a metastable material at pressures of at least 60 GPa (Fig. S9 and Fig. S10 in Supplementary Information).
The C3 phase starts to be energetically favorable above ~38 GPa when including ZPE, as shown in Fig. 3. Thus, the novel C3 phase can be synthesized in hydrogen-rich conditions at pressures starting from 38 GPa. This theoretical value agrees well with the experimentally observed formation at 45–50 GPa of a mysterious phase of unknown composition7,10. As shown in Fig. 4, calculations of the Raman shift23 reveal differences between the C2 and C3 phases in the H2-D2O system. The Raman shift of C3 phase, rather than an amorphous phase, agrees very well with the lower Raman frequencies of the vibron for the hydrogen molecules observed in Ref. [9]. The black rhombi in Fig. 4 indicate that some of the H2-D2O C3 sample encountered decomposition when quenched to low pressure. The variation of lattice parameters of the ice host structure in hydrates with pressure, revealed by our theoretical calculations, also agrees well with experimental XRD results10. At 55 GPa, our calculation gives lattice parameter of C3 phase a = b = 4.00 Å and c = 5.67 Å, corresponding to cubic ice sublattice with periodicity 5.67 Å, whereas experiment gives ~5.5 Å10.
Variations of the Raman shift of the vibron for the H2 molecules with pressure from experimental data in Ref. [9] and our theoretical calculations.
The red and black symbols are the experimental data for H2 vibrons in the H2-D2O sample. The blue open circles and squares indicate the Raman shift calculation for C2 and C3 phases of H2-D2O system, respectively.
At low pressure, the C2 adopts a “cubic ice” host structure and then transforms to a “tetragonal” one at ~20 GPa10 (Fig. S4 in Supplementary Information). When forming the C3 phase at increased pressure and in excess of H2, the ice host structure transforms to the “cubic ice” again. The change from tetragonal to “cubic” structure occurs before H-bond symmetrization transition happens in “tetragonal” type C2 at ~55 GPa. Thus, such structural transformation is unrelated to symmetrization of the H-bonds, but comes from the emergence of the C3 phase. For the hydrate C3, the H-bond symmetrization is predicted to occur at ~120 GPa (Fig. S5 in Supplementary Information), which is close the theoretical H-bond symmetrization pressure in ice-VII14.
Discussion
The C2 and C3 hydrates have a similar ice host framework, but the different numbers of hydrogen molecules and their different locations and orientations bring huge differences in phase stability range. In the C2 phase, hydrogen molecules stay in the centers of cages formed by water molecules in contrast to C3 phase, where they are located at the faces of the cages. To clarify the causes of stability of hydrogen hydrates, we used Bader analysis24,25 and focused on the C2 and C3 phases (Fig. S6 in Supplementary Information). We found a very small charge transferred from H2 to water molecules, so that the H2 molecules are slightly positively charged and H2O molecules carry a slight negative charge. The magnitudes of these charges are ~10−3–10−2 per molecule. This suggests that interactions between these molecules are almost purely steric, mainly related to packing density and shapes of the molecules. Comparing Bader volumes of the H2O and H2 molecules in the hydrates and in pure H2O and H2, we see that water molecules occupy slightly larger volume in the hydrates, whereas hydrogen molecules occupy much less space in C3 hydrate than in pure H2 – this leads to net densification, stabilizing this phase in a wide pressure range. For the C2 hydrate, the H2 molecules have lower volume than in pure H2 only at pressures below ~10 GPa, which explains its instability at higher pressures.
Having considered the PV -term in the enthalpy (H = E + PV), to get additional insight, we turned to the internal energy E and its changes when the H2 and H2O molecules are placed from the hydrate into pure H2 and H2O phases, while keeping molecular volumes fixed at their values in the hydrate (Fig. 5). This energy characterizes the net balance of the vdW attraction and steric repulsion between the molecules: this net effect is very small in the C3 phase (slightly destabilizing below ~30 GPa and slightly stabilizing above ~30 GPa). The remarkably wide stability field of the C3 phase is therefore mostly due to its high density and only to a small extent to more favorable intermolecular interactions. A much more interesting picture is observed for the C2 phase (Fig. 5a): we find its slight energetic stabilization below ~15 GPa and an increasingly large destabilization at higher pressures. This explains why C2 is unstable at high pressures and furthermore, it is clear that the increasing energetic instability of the C2 phase is responsible for the displacive phase transition, metastably occurring on overcompression and transforming the cubic H2O host sublattice into tetragonal, to enable better packing of the molecules.
Our calculations found that a C3-type phase is stable in the H2O–He system at 8–75 GPa (without including zero-point energy) and this phase is denser than the mixture of H2O and He. On the other hand, no such phase was found in the H2O-Ne system and indeed the C3 phase is not packing-efficient in this system (Fig. S7 and Fig. S8 in Supplementary Information). He and Ne are both chemically extremely inert, their almost only differences are size and (here insignificant) mass. Stability of He-C3 and instability of Ne-C3 hydrates reinforce our conclusion made for the H2O–H2 system, that stability of this novel phase comes not from specific bonding interactions between the molecules and not even their shapes, but is mostly due to their very efficient packing.
In summary, using the evolutionary algorithm USPEX, we explored the H2O–H2 system at pressures of up to 100 GPa. Stoichiometries and stability fields of H2O–H2 hydrate phases have been studied. A series of pressure-induced transformations found by theory closely coincides with experimental data, but also new insight was obtained. A novel Ih–C0 structure is predicted to have a very close enthalpy to the recently discovered C0 structure. At pressures above 38 GPa, novel hydrogen hydrate C3, based on cubic ice Ic, is predicted to be stable. With stoichiometry H2O:2H2, this is the hydrogen-richest hydrate known to date. With gravimetric density of easily removable hydrogen (18 wt.%), this is a promising hydrogen storage material that can find practical applications if its synthesis pressure can be decreased.
Methods
Crystal structure prediction
Predictions were done using the USPEX code in its variable-composition mode at several pressures (0, 1, 2, 5, 10, 20, 50 and 100 GPa) and zero temperature. A number of studies illustrate the power of the USPEX method26,27,28. We have done two types of variable-composition structure predictions in searching for all stable phases in the H–O system: (1) In the H–O system, assembling the structures from atoms and (2) In the H2O–H2 system with giving H2O and H2 molecules as structure building blocks. We have found that, even in the H–O system, all low-enthalpy states at pressures of our interest (<120 GPa) are actually made of well-defined H2O and H2 molecules. This allowed us to focus on molecular-type calculations, capable of efficiently dealing with large systems, without loss of rigor.
Given molecular nature of all stable and nearly stable compounds in this system, we searched for the packing of well-defined H2O and H2 molecules (rather than H and O atoms), by applying the specially designed constrained global optimization algorithm, considering structures with up to 24 molecules (i.e. up to 72 atoms) per primitive unit cell.
DFT calculations
Structure relaxations were done using density functional theory (DFT) within van der Waals (vdW) functional optB88-vdW29 in the framework of the all-electron projector augmented wave (PAW)30 method as implemented in the VASP31 code. The plane wave kinetic energy cutoff of 600 eV and Gamma-centered k-point meshes with the reciprocal space resolution of 2π × 0.05 Å were used. Having identified the most stable compositions and candidate structures, we relaxed them at pressures from 1 atm to 120 GPa with an even higher cutoff of 800 eV to refine their thermodynamic properties and stability fields. Structure relaxations proceeded until net forces on atoms were below 1 meV/Å, which gave us enthalpies converged to better than 1 meV/atom.
It is expected that the relative contribution of hydrogen bonding (H-bonding) and van der Waals (vdW) dispersion forces has a significant impact on the phase transition pressures and cohesive properties of the various crystalline ice phases32. This is also confirmed by our calculations for the phase transition pressures of ice phases from optB88-vdW, GGA33 calculations and experiments (Fig. S1 in Supplemental Information). Thus, all calculations included the vdW functional to treat the vdW forces, unless stated otherwise.
References
Vos, W. L., Finger, L. W., Hemley, R. J. & Mao, H.-K. Novel H2 - H2O clathrates at high pressures. Phys. Rev. Lett. 71, 3150–3153 (1993).
Vos, W. L., Finger, L. W., Hemley, R. J. & kwang Mao, H. Pressure dependence of hydrogen bonding in a novel H2O - H2 clathrate. Chem. Phys. Lett. 257, 524–530 (1996).
Mao, W. L. et al. Hydrogen clusters in clathrate hydrate. Science 297, 2247–2249 (2002).
Mao, W. L. & Mao, H.-K. Hydrogen storage in molecular compounds. Proc. Natl. Acad. Sci. USA 101, 708–710 (2004).
Lokshin, K. A. et al. Structure and dynamics of hydrogen molecules in the novel clathrate hydrate by high pressure neutron diffraction. Phys. Rev. Lett. 93, 125503 (2004).
Hirai, H., Ohno, S., Kawamura, T., Yamamoto, Y. & Yagi, T. Changes in vibration modes of hydrogen and water molecules and in lattice parameters with pressure for filled-ice hydrogen hydrates. J. Phys. Chem. C 111, 312–315 (2007).
Machida, S.-I., Hirai, H., Kawamura, T., Yamamoto, Y. & Yagi, T. Structural changes of filled ice ic structure for hydrogen hydrate under high pressure. J. Chem. Phys. 129, 224505 (2008).
Machida, S.-I., Hirai, H., Kawamura, T., Yamamoto, Y. & Yagi, T. Structural changes and intermolecular interactions of filled ice ic structure for hydrogen hydrate under high pressure. J. Phys.: Conf. Ser. 215, 012060 (2010).
Machida, S.-I., Hirai, H., Kawamura, T., Yamamoto, Y. & Yagi, T. Isotopic effect and amorphization of deuterated hydrogen hydrate under high pressure. Phys. Rev. B 83, 144101 (2011).
Hirai, H. et al. Structural changes of filled ice ic hydrogen hydrate under low temperatures and high pressures from 5 to 50 GPa. J. Chem. Phys. 137, 074505 (2012).
Strobel, T. A., Somayazulu, M. & Hemley, R. J. Phase behavior of H2 + H2O at high pressures and low temperatures. J. Phys. Chem. C 115, 4898–4903 (2011).
Efimchenko, V. et al. New phase in the water–hydrogen system. J. Alloy. Comp. 509, Supplement 2, S860–S863 (2011).
Lenz, A. & Ojamäe, L. Structures of the I-, II- and H-methane clathrates and the Icemethane clathrate phase transition from quantum-chemical modeling with force-field thermal corrections. J. Phys. Chem. A 115, 6169–6176 (2011).
Zhang, J., Kuo, J.-L. & Iitaka, T. First principles molecular dynamics study of filled ice hydrogen hydrate. J. Chem. Phys. 137, 084505 (2012).
Loveday, J. S. & Nelmes, R. J. High-pressure gas hydrates. Phys. Chem. Chem. Phys. 10, 937–950 (2008).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, – (2006).
Oganov, A. R., Ma, Y., Lyakhov, A. O., Valle, M. & Gatti, C. Evolutionary crystal structure prediction as a method for the discovery of minerals and materials. Rev. Mineral. Geochem. 71, 271–298 (2010).
Oganov, A. R., Lyakhov, A. O. & Valle, M. How evolutionary crystal structure prediction works—and why. Acc. Chem. Res. 44, 227–237 (2011).
Zhu, Q., Oganov, A. R., Glass, C. W. & Stokes, H. T. Constrained evolutionary algorithm for structure prediction of molecular crystals: methodology and applications. Acta Crystallogr., Sect. B: Struct. Sci 68, 215–226 (2012).
Zhu, Q. et al. Stability of xenon oxides at high pressures. Nat. Chem. 5, 61–65 (2012).
Pickard, C. J. & Needs, R. J. Structure of phase III of solid hydrogen. Nat. Phys. 3, 473–476 (2007).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Lazzeri, M. & Mauri, F. First-principles calculation of vibrational raman spectra in large systems: Signature of small rings in crystalline SiO2 . Phys. Rev. Lett. 90, 036401 (2003).
Bader, R. F. W. Atoms in Molecules - A Quantum Theory (Oxford University Press, 1990).
Henkelman, G., Arnaldsson, A. & Jonsson, H. A fast and robust algorithm for bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006).
Hu, C.-H. et al. Pressure-induced stabilization and insulator-superconductor transition of bh. Phys. Rev. Lett. 110, 165504 (2013).
Zhu, Q., Oganov, A. R. & Lyakhov, A. O. Novel stable compounds in the Mg-O system under high pressure. Phys. Chem. Chem. Phys. 15, 7696–7700 (2013).
Zhang, W. et al. Unexpected stable stoichiometries of sodium chlorides. Science 342, 1502–1505 (2013).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Santra, B. et al. Hydrogen bonds and van der waals forces in ice at ambient and high pressures. Phys. Rev. Lett. 107, 185701 (2011).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
We thank the National Science Foundation (EAR-1114313, DMR-1231586), DARPA (Grants No. W31P4Q1210008 and No. W31P4Q1310005) and the Government (No. 14.A12.31.0003) of Russian Federation (Project No. 8512) for financial support and Foreign Talents Introduction and Academic Exchange Program (No. B08040). We also thank Purdue University Teragrid and TACC Stampede system for providing computational resources and technical support for this work (Charge No.: TG-DMR110058).
Author information
Authors and Affiliations
Contributions
G.R.Q., A.O.L., Q.Z., A.R.O. and X.D. designed research, performed simulations, analyzed data and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Novel Hydrogen Hydrate Structures under Pressure
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Qian, GR., Lyakhov, A., Zhu, Q. et al. Novel Hydrogen Hydrate Structures under Pressure. Sci Rep 4, 5606 (2014). https://doi.org/10.1038/srep05606
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05606
This article is cited by
-
Significance of the high-pressure properties and structural evolution of gas hydrates for inferring the interior of icy bodies
Progress in Earth and Planetary Science (2023)
-
Emergence of superconductivity in doped H2O ice at high pressure
Scientific Reports (2017)
-
Diverse Chemistry of Stable Hydronitrogens, and Implications for Planetary and Materials Sciences
Scientific Reports (2016)
-
Novel Stable Compounds in the C-H-O Ternary System at High Pressure
Scientific Reports (2016)
-
New porous water ice metastable at atmospheric pressure obtained by emptying a hydrogen-filled ice
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.