Abstract
Despite the extensive use of in-vitro models for neuroscientific investigations and notwithstanding the growing field of network electrophysiology, all studies on cultured cells devoted to elucidate neurophysiological mechanisms and computational properties, are based on 2D neuronal networks. These networks are usually grown onto specific rigid substrates (also with embedded electrodes) and lack of most of the constituents of the in-vivo like environment: cell morphology, cell-to-cell interaction and neuritic outgrowth in all directions. Cells in a brain region develop in a 3D space and interact with a complex multi-cellular environment and extracellular matrix. Under this perspective, 3D networks coupled to micro-transducer arrays, represent a new and powerful in-vitro model capable of better emulating in-vivo physiology. In this work, we present a new experimental paradigm constituted by 3D hippocampal networks coupled to Micro-Electrode-Arrays (MEAs) and we show how the features of the recorded network dynamics differ from the corresponding 2D network model. Further development of the proposed 3D in-vitro model by adding embedded functionalized scaffolds might open new prospects for manipulating, stimulating and recording the neuronal activity to elucidate neurophysiological mechanisms and to design bio-hybrid microsystems.
Similar content being viewed by others
Introduction
Several studies have been devoted to the introduction of in-vitro 3D neuronal systems but the use of such experimental models is still limited and, as far as we know, no attempt of functional multisite electrophysiological measurements of 3D neuronal networks has been presented in the literature. The potential advantages of 3D engineered constructs are evident as they can be used as a more accurate investigational in-vitro platform or as the basis for developing living bio-hybrid neuro-electronic microsystems in-vitro or in-vivo1. Thus the design and implementation of 3D engineered neuronal networks with embedded sensors and recording-stimulating electrodes, would give new opportunities for investigations and applications in the neuroscientific domain. On the other hand, the development of such 3D network architectures and the possibility of chronic and functional electrophysiological recordings pose new challenges in terms of integration between scaffolds and recording-stimulating devices, long-term cell survival, exchange of nutrients, cell coupling with micro-electrodes and micro-sensors, etc. Till now, most of the efforts have been devoted to the development of new materials2, passive3,4 and active scaffolds5 and new experimental procedures to guarantee the development of 3D cultured networks; however, multi-site electrophysiological recordings in such 3D neuronal preparations are still lacking.
Nowadays, the standard and well-accepted experimental model for neurophysiological studies is constituted by cultured networks grown onto (stiff) planar substrates also with embedded micro-electrode arrays (MEAs)6. As recently pointed out, besides clear advantages related to controllability and observability, such 2D neuronal model systems have major limitations, as they might be inherently unable to exhibit characteristics of in-vivo systems. For example, soma and growth cones in 2D are unrealistically flattened and the axons-dendrites outgrowth cannot occur in all directions1. Nevertheless, such in-vitro 2D experimental models have been used to investigate mechanisms of coding and information transmission7, network plasticity and functional connectivity8,9 and memory10. Although these model systems are somehow widely accepted, one of the raised major issues has often been related to the dynamics exhibited by such networks, which are often dominated by bursting activity encompassing most of the neurons in the network11. Under this perspective the development of a true 3D engineered in-vitro neuronal model can certainly be seen as a complementary-alternative and interesting tool for neurophysiological investigations.
In this work we report a first study about the spontaneous and electrically evoked electrophysiological activity in 3D hippocampal neuronal cultures coupled to substrate with embedded planar MEAs. 3D neuronal constructs were developed and implemented by using glass microbeads12 to design engineered in-vitro systems where thickness of the preparation, cell density and network connectivity are partly controlled to resemble brain tissue while enabling, at the same time, optical observation, environmental control and multisite electrical recording-stimulation. The culturing method and coupling with MEAs is simple, reliable and efficient and it can be easily extended to other brain areas (e.g., cortex) and tailored to other types of planar MEAs (e.g., high-density micro-electrode array13,14) or integrated with 3D multi-electrodes.
Results
We anticipate that the main result is a true 3D neuronal network model coupled to planar MEA that shows a wide range of activity patterns. These recorded patterns are variable and present striking differences from the dynamics of homogeneous-uniform sister cultures grown onto the planar MEA substrate both during spontaneous and electrically stimulated activity.
3D neuronal network construction
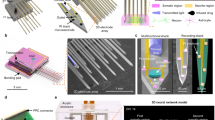
Layers of glass microbeads of a selected dimension constitute the basic structure for designing and implementing 3D neuronal networks. In order to build the hippocampal assembly, we used microbeads of 40 μm in diameter that self-assembled in a compact hexagonal geometry and that provided both a reasonable growth surface for neurites and a large enough interstitial space for cell bodies12. The microbeads were sterilized and pre-treated with a mixture of adhesion factors, Laminin and Poly-D-Lysine (both 0.05 μg/ml), at 37°C for 12 hours. At this stage, about 30·103 microbeads were placed onto a Transwell® porous membrane where they self-assembled forming a uniform layer. For the direct coupling with neurons, we then seeded dissociated hippocampal cells (concentration of 700 cells/μl) on the coated monolayer of microbeads (Figure 1b, first panel) and cultured them in Neurobasal medium (see Methods). The cell seeding concentration was chosen in order to obtain a final density of about 1,500 cells/mm2 covering the microbeads surface and approaching a confluent monolayer. Meanwhile, we plated the hippocampal neurons onto the MEA surface, which was previously pre-coated with adhesion factors (Laminin and Poly-Lysine both at 0.05 μg/ml), in a delimited area obtained by coupling a Poly-dimethyl-siloxane (PDMS) structure to the MEA substrate. The confinement (Figure 1a, first panel) was used to allow cell plating preferentially onto the active electrode area of the device and subsequently to accommodate for the glass microbeads stacks with adherent neurons (Figure 1b). The PDMS structure was constituted of a simple cylinder (built with the molder shown in Figure 1a, second panel), with an external and internal diameter of 22.0 and 3.0 mm respectively and with a height of 650 μm. The final configuration, composed of MEA device, PDMS structure, microbeads and neurons layers, is shown in the third panel of Figure 1a. We wish to underline that the 2D neural network (cell density of 1,800–2,000 cells/mm2) directly coupled to the active area of the MEA was fundamental to ensure a good communication between the substrate embedded micro-electrodes and the 3D assembly.
Construction of 3D neural networks.
(a). From left to right: PDMS structure allowing to confine microbeads and neurons on the recording site area; molder used to build the confinement structure; cartoon that illustrates the final configuration (multi-layers of microbeads and neurons confined by a PDMS structure onto the active area of the Micro-Electrode Array). (b). Main steps for building a 3D neural network. Microbeads were placed onto a porous Transwell® membrane where they self-assembled in a hexagonal geometrical structure; dissociated hippocampal cells were plated on such coated microbeads. To obtain a 3D structure, the suspension of neurons and microbeads was then moved from the membrane to the MEA surface several times (details can be found in the Results Sec.). The last sketch depicts the recording/stimulation configuration: the electrophysiological activity of the 3D network is recorded from the substrate MEA electrodes (bottom layer); the network is stimulated by using both MEA and tungsten electrodes (bottom and top layers). (c). Experimental configurations: 3D neural network; 2D neural network; Control 1 i.e., network constructed among beads plated on MEA; Control 2 i.e., 2D network plated onto MEA with bare beads on top.
After 8–10 hours, the suspension of neurons and microbeads was moved from the Transwell® membrane and deposited over the 2D neuronal network previously plated onto the area defined by the PDMS structure (Figure 1b, second panel). With respect to the original density, we estimated a loss of about 20–30% of cells due to mechanical manipulations and to cell bodies that remained on the surface of the Transwell® membrane. Once the first layer was deposited, we repeated the same operation to obtain a packed 3D assembly (Figure 1b, third panel). The resulting 3D structure rearranged itself to form a colloidal crystal, which self-assembled in a (theoretically) hexagonal structure composed, on average, by 5–8 layers of microbeads and cells. Once all the layers were spontaneously assembled, neuronal processes grew over the microbead scaffold resulting in a high-density physically connected 3D neural network, with an estimated (on the basis of the actual volume and total number of transferred neurons) final cell density of about 80·103 cells/mm3, a value in the range of the interstitial density computed for glass microbeads of 40 μm in diameter (1·105 mm−3). It is worth noting that this value is not far from 92·103 cells/mm3, the average neuronal density reported for the mouse brain cortex15. Indeed, by adjusting the microbeads dimensions, we could change-control the density of the neurons and partly control the average connectivity degree of the network12.
The final configuration is represented in the cartoon of the last panel of Figure 1b, where it can be observed that the electrophysiological activity of the bottom (i.e., read out) layer can be easily recorded by the electrodes of the MEA substrate. In addition, the developed set-up allowed us to deliver an electrical stimulation both from the bottom layer through the MEA electrodes and from the top layers by using a conventional tungsten electrode (see Methods).
To characterize the electrophysiological activity of the 3D network (Figure 1c, first panel) and to demonstrate how the 3D structure modulates the network dynamics, we specifically compared the expressed dynamics with homogeneous-uniform 2D neuronal networks grown over MEAs (Figures 1c, second panel) and with two additional controls. The first control (Control 1) was implemented to verify whether the electrical activity generated only by 3D networks assembled onto the microbeads (i.e., 3D networks coupled to bare MEAs) was possibly captured by the substrate MEA (Figure 1c, third panel). The second control (Control 2) was constituted of uniform 2D neural networks plated onto MEAs assembled with around 5–8 layers (i.e. without neurons) of bare microbeads (Figure 1c, fourth panel) to verify whether the electrophysiological activity of 2D networks was affected by the presence of a microbead stack on top of the cell culture.
Imaging characterization
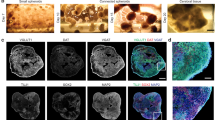
In order to prove in-vivo like cell morphology and demonstrate the reliability of implementing a 3D network, we gathered structural information on fixed 3D hippocampal cultures by indirect immunofluorescence techniques. For this purpose we prepared sister cultures on glass coverslips that were fixed with PFA 4% (see Methods) together with the 3D-MEA cultures at the end of each recording session. We treated the different coverslip-grown cultures with a selected panel of primary and secondary antibodies in sequence. The use of coverslip-coupled (thickness 0.13–0.14 mm) 3D cultures was necessary to overcome the limitation introduced by the relatively high thickness (~1 mm) of the MEA glass substrate that precluded the possibility of using high numerical aperture objectives with an inverted confocal microscope. The configuration of the 3D-coverslip cultures was identical to the final structure of the hippocampal 3D-MEAs. Hippocampal neurons were plated by the same procedures (see Figure 1b and Methods) and for the same period. We also used an up-right confocal microscope to complete our tridimensional optical analysis. The objective was immersed inside the MEA reservoir where the multilayered structure of microbeads was assembled. In this scenario, we used long-working distance objectives, to observe the morphology of the neural network within the deepest layers with a z-stack exceeding 400 μm. The pictures in Figure 2 show the different configurations investigated: from 2D cultured hippocampal neurons to 3D networks coupled to MEAs (4th week in-vitro). Particularly, Figure 2a shows a close-up of a few cells cultured on a planar substrate and Figure 2b shows a small cluster of neurons with embedded microbeads in which a GABA and NeuN positive neuron (top left) and four NeuN positive (putative excitatory) neurons can be observed. It is worth noting the round shape of the cell bodies with respect to the flattened shape of the surface plated neurons. Panels c–f of Figure 2 show a sequence of the microbead stack and neurons (also visible as Supplementary – Movie 1) on a glass coverslip. On the orthogonal projection of the y-axis it can be observed some cell bodies lie on the glass surface while others remain entrapped among the microbeads in the interstitial spaces (see also Supplementary – Movie 2). Figure 2g shows extensive encapsulation by neuritic processes (MAP-2 positive) around the microbead scaffold indicating a high-density of potential connectivity among neurons. Finally, Figure 2h and 2i show the floor of the 3D networks (with the substrate embedded microelectrode) and a nice occupancy of the interstitial space and extensive arborizations connecting the neurons. In general, we can underline a main difference in the development of the axo-dendritic processes. The growth of 3D network shows patterns of tangled ramifications both across and along different layers (5–8 layers, see Supplementary – Movie 3) and around the single microbead. This new network configuration gains a wide range of extension (see Supplementary – Movie 4) compared to the 2D model and, although constrained by the presence of the microbeads ordered reticulum, each neuron, in principle, can have a site density of connecting points that is inversely dependent on the beads radius cubed12. Considering the close relationship between the spontaneous electrophysiological activity and the level of synaptic expression16, we can assume that the large number of synaptic puncta visible in Figure 2c–f (see also Supplementary – Movie 1) is an indication of a possible high connectivity degree within the new network model. From these 3D neural networks we could estimate a synaptic density of about 2.6·107 synapses/mm3 (see Supplementary - Fig. S1, a–c), value that is an order of magnitude less than what is reported for the mouse cortex15. By considering the average neuronal density of the 3D model (80·103 cells/mm3) and the estimated synaptic density, we obtained about 600 synaptic connections per neurons. As a reference, we also estimated the average number of synapses per neuron of the considered 2D neuronal cultures (see Supplementary – Fig. S1 d–e) obtaining also in this case an average density of ~600 synapses/neuron17.
Imaging characterization.
(a). Mature hippocampal neurons (4th week in-vitro), cultured on a planar substrate (i.e., 2D standard model, positive for Map-2 and Dapi nuclear dye). Scale bar: 20 μm. (b). Small cluster of neurons and microbeads closely linked together by a GABA interneuron (green/red) and four Nuclear Neuronal protein NeuN positive neurons (red). Scale bar: 20 μm. (c–f). z-stack sequence of 3D cultured hippocampal neurons fixed at DIV (Days In Vitro) 28 and immunolabeled for the pre-synaptic marker Synapsin (green) and NeuN (red). Scale bar: 10 μm. (g). 3D rendering of 261.4 μm z-stack of the hippocampal network on MEA device showing a high density of neuronal processes, exposed to dendritic marker MAP-2. Scale bar: 40 μm. (h). 3D culture on MEAs, labeled with MAP-2 and NeuN. Scale bar: 40 μm. (i). The first layer of microbeads directly coupled to the top of a single micro-electrode. Scale bar: 20 μm. Note: secondary antibodies for all images are Alexa Fluor 488 or Alexa Fluor 546 conjugated with Goat anti mouse or Goat anti rabbit.
Spontaneous activity
Spontaneous activities of 2D (n = 28) and 3D (n = 39) neural networks were recorded for 30 min after 3–4 weeks in culture. Comparisons with control experimental cultures (3D cultures on bare MEA – Control 1 and 2D cultures coupled to bare 3D microbeads structures – Control 2) were also carried out, to verify possible unwanted effects not attributable to the development of a true 3D network. All cultures were initially investigated with both excitation and inhibition active. The role of inhibition in network dynamics is treated later.
First of all, the spontaneous activity of 3D hippocampal neuronal networks was successfully recorded in all the reported experiments by means of planar TiN 60 channels MEAs (see Methods). The electrophysiological activity of the 3D networks was then analyzed and compared with the uniform 2D hippocampal cultures and with the two additional control conditions (Figure 1c). As reported in the literature7,11,18, 2D uniform hippocampal and cortical neuronal networks show a typical electrophysiological activity in the mature phase of their development (i.e., after 3–4 weeks in-vitro) characterized by oscillating dynamics and synchronous bursts involving most of the active channels in the MEA. Figure 3a shows 5 min of the spontaneous activity of a representative experiment performed on a 2D hippocampal culture during the fourth week in-vitro. Also in our recordings, we found a quasi-synchronous activity and a network dynamics composed mainly of network bursts (NB) (i.e., synchronized events that involve most of the recording channels; see Methods). Looking closer at the raw data of a single channel, one can see that these bursts are characterized by an amplitude of about 100 μV and a duration of about 300 ms (see also Supplementary – Movie 5). Similarly, Figure 3b shows a raster plot of the spontaneous activity of a representative experiment of a sister culture (i.e., same batch) forming a 3D network at the same age of its development (i.e., fourth week). It can be noticed that the signature of the network dynamics presents a wider repertoire of activities with less global synchrony and more pronounced spiking at a single channel-neuron level. From a preliminary qualitative observation, we can see periods in which the network holds a more synchronous activity (red box) similar to what observed in the 2D networks. In this case bursts are characterized by a similar amplitude (i.e., about 100 μV), but by a longer duration (up to 1 s, see raw data of a single channel displayed in figure 3b top; see also Supplementary – Movie 5). As anticipated, the 3D neural network exhibits also a significant ‘random spiking’ and non-synchronous bursting activity (blue box). To highlight these two distinct ‘modes’ of firing, we computed (cf. boxes of Figure 3b) the Instantaneous Firing Rate (IFR) profiles (see Methods). The same plot for the 2D network (Figure 3a), relative to the green region, shows a very high synchronous activity and the absence of significant random spiking activity.
Spontaneous activity characterization.
Electrophysiological activity of a representative neuronal network, (a). 2D and (b). 3D. From top to bottom: example of 10 s of raw data recorded from one microelectrode; raster plots showing 300 s of spontaneous activity. For the highlighted areas, the Instantaneous Firing Rate (IFR) profile is shown. For the 3D network, the blue and red boxes highlight random spiking and network bursting activity regions, respectively. For the 2D network, only network bursting regions can be detected (green box). (c). Percentage of random spikes, (P-value = 10−4, Mann-Whitney U-test). (d). Mean Bursting Rate (P-value = 10−4, Mann-Whitney U-test). (e). Burst Duration. (f). Mean Network Bursting Rate (P-value = 9·10−4, Mann-Whitney U-test). (g). Network Burst Duration (P-value = 9·10−4, Mann-Whitney U-test). (h). Inter Burst Interval distribution with a bin size of 0.5 ms. Parameters were evaluated over the entire dataset. Asterisks above the plots indicate statistically significant differences.
The previous observations were further globally quantified by evaluating the percentage of random spikes (i.e., the fraction of spikes outside bursts) in all the performed experiments (Figure 3c). 2D networks exhibit a strong synchronous bursting activity with a low percentage of random spikes (15.9 ± 2% (mean ± standard error of the mean)), differently the 3D networks show a significant higher level of random spiking (33.8 ± 3%; P-value = 10−4, Mann-Whitney U-test). In order to quantify the bursting activity at the single channel level, the frequency and the duration of the bursts were evaluated in all the performed experiments (Figure 3d–e respectively). 2D networks presented a much higher level of bursting rate (19.7 ± 1.1 burst/min) than 3D neural networks (5.2 ± 0.4 burst/min, P-value = 10−4, Mann-Whitney U-test), while burst durations are not significantly different between the two. Even if network bursting remains a common signature for both preparations, the shift from 2D to 3D did also affect the bursting behavior as the main effects are observed in both frequency and duration. Then, we computed the network mean bursting rate and duration evaluated over the entire dataset (Figure 3f–g respectively). In 2D neural network the network mean bursting rate is high (22.3 ± 3.8 NB/min) with a nearly constant duration (540 ± 5 ms); differently, the 3D networks exhibit few network bursts (3.0 ± 0.6 NB/min, P-value = 9·10−4, Mann-Whitney U-test) with a high duration (919 ± 65 ms, P-value = 9·10−4, Mann-Whitney U-test). The high value of the standard error for the 3D networks indicates a much higher variability of bursting activity. Further, we evaluated the Inter Burst Interval (IBI) distributions for both 2D and 3D neural networks (Figure 3h). For the uniform 2D networks, about 90% of the burst intervals were distributed within the first 2.5 s and only 1% of the burst showed IBIs greater than 5 s. For the 3D networks, IBIs are much shorter and about 40% of the burst intervals are in the first bin (0.5 s). The remaining distribution is much broader and covers intervals up to 10–15 s. We also challenged the presented 3D model with the addition of bicuculline (BIC, 25 μM) to test whether, by blocking GABA transmission, we had a different effect on 3D networks with respect to uniform 2D cultures. We found that, starting from different spontaneous dynamics, the administration of BIC steered both 2D and 3D neuronal networks towards the same more synchronized dynamic state (see Supplementary – Figure S2) with a similar percentage of random spike and NB duration (Figure S2d and h). Interestingly, also the IBI distributions become similar after the addition of BIC.
We also quantified the level of synchronization and correlation of the network activity by means of the cross-correlation (CC) function (see Methods) computed for 2D and 3D neural networks with a time window of 2 s and a bin size of 5 ms. For 3D neural networks, CC was also specifically evaluated within the random spike activity and within the burst activity regions. CC function for a 2D network (Figure 4a) underlines a high level of correlation among a representative channel and all the other recording channels. The CPeak values (i.e., maximum values of the CC function) for all the active channels are close to one (0.85 ± 0.03). On the contrary, for a 3D network we can see a low level of correlation among a representative channel and all the other active channels in the random spike activity region (Figure 4b). The mean CPeak value is low (0.42 ± 0.02) and the peaks values are shifted with respect to the central bin suggesting possible causal relationships mediated by the neuronal populations above the read-out layer. Within the burst activity region, the level of correlation among channels is high (mean CPeak value of 0.70 ± 0.02) and the majority of peaks is centered in the central bin (Figure 4c). We further characterized the level of synchronization of the 2D and 3D network activity by computing the values of the CC function in the central time bin (i.e., C(0)). 2D neural networks exhibit a high level of synchronization as the normalized C(0) values are close to one for the majority of the recording channels (Figure 4d). The level of synchronization of the 3D neural network activity is high during the period of bursting (C(0) close to one as for the 2D networks – Figure 4f) while it is very low (Figure 4e) within the random spike activity region. In order to better identify the synchronized channels within this region, we compared the C(0) values with a threshold related to the average C(0) values (see Methods). Only five channels presented a value of C(0) higher than the threshold (these channels are highlighted in pink in the raster of Figure 3b) and they represent a group of spatially confined electrodes that could suggest the presence of a synchronized sub-population. Putative assembly of neurons can be individuated by higher C(0) values shown in the 8 × 8 color map layout which represents also the physical position of the MEA channels (Figure 4g–i). In the 2D neural network several channels present a maximum C(0) value; in the 3D network (within the random spike activity regions; 3D-rs) there is only one channel with a maximum C(0) value (autocorrelation) and there are few channels with a C(0) value greater than 0.5. In the 3D burst activity regions (3D-b), beside the autocorrelation, almost all the other channels exhibit a C(0) value greater than 0.7. The previous observations were globally quantified by evaluating the C(0) values for all the performed experiments (Figure 4j). 2D neural networks present a mean C(0) value close to one (0.81 ± 0.02), suggesting a very high synchronization among all the channels. The level of synchronization in 3D neural networks is high within the burst activity region (mean C(0) value of 0.71 ± 0.04) and low within the random spike activity region (mean C(0) value of 0.46 ± 0.02). Data differences are significant (P-value < 10−6, Mann-Whitney U-test). To prove such activity variability was supported by the development of a true 3D architecture, we compared the exhibited 3D dynamics with the activity of the Controls presented in Figure 1c. As it might be expected, in the case of Control 1 (n = 5), almost no activity was recorded (see Supplementary – Fig. S3a). This behavior is due to the assembly procedure by which neurons are only seeded within the microbead structure, thus resulting in a bad coupling of the cell bodies to the MEA substrate (see Figure 1c). It should be underlined that only with a good contact (i.e. effective adhesion) between neurons and microelectrodes we can reliably record electrophysiological signals19. In the case of Control 2 (n = 5), the electrophysiological activity was, as expected, very similar to the 2D neural network (see Supplementary – Fig. S3b). Moreover, we compared the activity of Control 2 with the activity of uniform 2D neural networks, by evaluating the percentage of random spikes, the NB duration and the C(0) values for all the performed experiments (see Supplementary – Fig. S3c, S3d, S3e). These results clearly indicate that the presence of a 3D network organization introduces a great variability in the electrophysiological activity recorded at the bottom layer, by inducing partly synchronized sub-populations and breaking down the uniform and stereotyped behavior of uniform high density 2D neuronal networks20.
Cross-Correlation analysis relative to 2D and 3D neural networks.
(a–b–c). Cross Correlation function between one representative channel and all the other recording channels evaluated for the 2D neural networks, 3D neural networks within the random spike activity region and 3D neural networks within the burst activity region. CC is computed with a time window of 2 s and a bin size of 5 ms. The color code indicates the normalized function values (minimum and maximum values are depicted in blue and red respectively) (d–e–f). C(0) values for 2D and 3D networks. These values are obtained taking into account the Cross Correlation function reported in panels (a–b–c). The correlation between one channel (blue bar) and the other recording channels is computed. The 3D network C(0) is computed within both the random spike activity and the burst activity regions. These values are compared with a threshold (red dashed line). The blue bar identifies the autocorrelation value; the electrodes that show a C(0) value higher than the threshold are visualized with red bars. (g–h–i). Colormaps showing the C(0) values reported in panels (d–e–f) in a 8 × 8 layout. (j). C(0) values evaluated for 2D networks (white), 3D networks within the random spike activity region (gray) and 3D networks within the burst activity region (striped gray). Parameters are evaluated over the entire dataset. Asterisks above the plots indicate significant differences (P-value < 10−6, Mann-Whitney U-test).
To demonstrate whether the layers of the 3D structures were effectively connected and capable of inducing significant differences in the recorded dynamics, we studied and characterized the propagation of the electrophysiological signals in the read-out layer (i.e., the bottom layer of the neurons coupled to the planar MEA). In the 2D neural networks, the signal propagation is indubitably continuous (see Supplementary - Movie 5). Bursts start from few sources and propagate rapidly and in a continuous way invading the whole network, as also observed in calcium imaging recordings21. In the 3D networks, the signal that starts from one site looks as if it propagates in the network in a discontinuous way (see Supplementary - Movie 5). The observed variability measured at the read-out layer can be explained by considering a propagation also in the z-direction. To confirm the impression of activity propagation also in the upper layer of the 3D networks, we evaluated the ignition sites from which the NBs started. We defined such ignition sites as the sites where bursts initiate in at least 5% of all the NBs22. Moreover, we accounted for the latency of the subsequent spikes in all the recording electrodes (i.e., the time between consecutive spikes in another electrode involved into the NB starting from the same source). Figure 5a shows the occurrence of single sources for 30 min of activity of a representative 2D network. It is worth noting that only three major sources were individuated. Furthermore, such signal sources were stable in time as we evaluated the occurrences of these three electrodes by dividing the recorded interval in phases of 5 min each. The three sources were present in all the four considered experimental phases (Figure 5b). Figure 5c shows the map of the mean latency (interpolated propagation fronts, isochrones) between a chosen electrode (source) and the spikes which follow in all the electrodes involved in the NBs initiated by that electrode23. Following the same approach, we analyzed the signal propagation during NBs in a representative 3D network. We found a large number of sources with low occurrences (Figure 5d) and by evaluating the signal sources in consecutive 5 min experimental phases, we found a great variability (Figure 5e) as different sources are seemingly detected in different phases. The isochrones map (Figure 5f) displays a discontinuous propagation of the signals with long time delay. The previous illustrative results were further globally quantified by evaluating the number of NBs and the relative detected sources in six different experiments (Figure 5g). The number of NB exhibited by the 2D networks was higher (thick gray bars) compared to the number of NB in 3D networks. Indeed, we found more ignition sites (thin black bars), in the 3D networks than in the 2D ones. Summarizing, 2D networks exhibited a lot of NB with few sources; 3D networks few NBs with more seeming sources (Figure 5g, inset). We also looked at possible correlations between latency and distance. For 2D networks, we found a linear relationship between distance and latency for all the analyzed experiments (R2 = 0.67; Figure 5h, black line). The estimated speed of propagation was 42 ± 3.5 mm/s, value comparable with previous works21,24,25. From the 3D networks (Figure 5i), we could not extract a good correlation between latency and distance (R2 = 0.07; black dashed line) meaning that only random latencies (up to 100 ms), with respect to the distance, were observed in the read-out layers of neurons coupled to the planar MEA.
Signal propagation.
(a). Signal sources evaluated in 30 min of spontaneous activity of a representative 2D network. The number of occurrences for each electrode that ignites a burst is reported. The 5% threshold is indicated by a dashed red line and the three putative sources are indicated with arrows. (b). Occurrences of 2D network signal sources evaluated in four recording phases of 5 min each. (c). Isochrones of the propagating signals. The considered source is indicated with a bold point (electrode 52). (d). Signal sources evaluated in 30 min of spontaneous activity of a representative 3D network. The number of occurrences for each electrode that ignites a burst is reported. The 5% threshold is indicated by a dashed red line and the eight putative sources are indicated with arrows. (e). Occurrences of 3D network signal sources evaluated in four recording phases of 5 min each. (f). Isochrones of the propagating signals. The considered source is indicated with a bold point (electrode 16). (g). Number of NB (grey bars) and number of sources (black bars) evaluated in the 30 min of recording for six experiments. The means of the NB and source number are reported in the inset. (h). Distance-latency relationship for 2D neural networks; each color represents a single experiment. The black line indicates the global fitting of the data (R2 = 0.67); the plot on the right reports the fittings for the single experiments. (i). Distance-latency relationship for 3D networks; each color represents a single experiment. The black dashed line indicates the global fitting of the data (R2 = 0.07). 2D and 3D neural network correlation coefficients are statistically different (P-value < 10−6, Mann-Whitney U-test).
The discontinuity in the propagation and the seeming variability of the signal sources, are all indirect proofs that signals propagate in the upper layers and support the hypothesis of the presence of signal sources in the upper layers.
Stimulus-evoked activity
To further support the previously presented results and to ultimately demonstrate whether the layers were functionally connected (i.e., synaptic pathways cross the assembly in all the directions of the 3D space), we performed experiments by delivering electrical stimulation with two different experimental protocols-settings. We stimulated from the bottom layer 3D (n = 15) and 2D (n = 7) cultures by using one of the electrodes of the substrate MEA; we performed top-layer stimulation on 3D cultures (n = 3) by means of a bipolar tungsten electrode. The experimental configuration is illustrated in the last panel of Figure 1b.
Figure 6 shows the Peri Stimulus Time Histograms (PSTHs) over a 4 × 4 grid (a subset of the channels of the 8 × 8 MEA layout) with the different evoked activities that the network exhibited in response to the applied stimulation. To examine the network response characteristics, we evaluated the time in which the 60% of the PSTH area occurred (t60). The vertical red bars in Figure 6 indicate such t60 value. In the 2D network, the neural response to the stimulation delivered by the bottom layer (2D-Bottom) was, as expected26, similar for all the responding channels (Figure 6a). The highest response peak (i.e., the maximum of the evoked response) was detected immediately after the stimulation; then the number of evoked spikes exhibited a decreasing trend that goes to zero in about 1 s. The 60% of the evoked spikes (see red bar, t60) was confined to the first hundreds of milliseconds. In the case of the considered 3D networks stimulated by the MEA (Figure 6b, 3D-Bottom), the PSTH profiles presented a more pronounced variability. Some electrodes displayed a large response immediately after the stimulation. In other cases, the response peak was up to 1 s after the stimulation. In the highlighted case, the single channel PSTH profile indicated the 60% of response was within the first 700 ms. These results indirectly prove by themselves that additional synaptic pathways were involved and elicited when stimulated from the bottom layer (MEA substrate) and that possible reverberating paths going up and down into the 3D microbead layers contributed to the observed delayed responses. The last analyzed case concerns the 3D network response to a stimulation delivered by the top layers (Figure 6c, 3D-Top). As it might be expected, in this configuration not many channels (less than 50%) detected a neural response, suggesting that a reduced number of synaptic pathways reached the bottom layer. This could be an indication that the connectivity along the z-direction was less effective or that the synaptic density decreased from bottom to top. However, for the responsive channels, the evoked activity was quite different from the previous ones. The t60 (i.e., red bars) spanned over a wide time window and electrodes exhibited a t60 value exceeding 1 s. Finally, no response was recorded in the Control 2 condition from top stimulation, indicating there was no wide field effect of the stimulation.
2D and 3D neural network response to electrical stimulation: PSTH profiles.
The PSTH profiles are depicted over a 4 × 4 grid, representing a subset of the most responsive electrodes of the MEA. The red vertical bar indicates the time instant in which the 60% of the PSTH area occurs. The cross indicates the electrode position from which the stimulus is delivered. (a). 2D neural network response to stimulation and single channel PSTH profile. (b). 3D neural network response to the stimulation delivered from the bottom layer and single channel PSTH profile. (c). 3D neural network response to the stimulation delivered from the top layer and single channel PSTH profile.
In the illustrative case of Figure 7, for the 2D network stimulated from the bottom layer, the responses were close to the stimulation time (Figure 7a) and, for the majority of the channels, the 60% of the PSTH area (i.e., t60) was detected within the first 250 ms (Figure 7d) with all the electrode responding the same way. For the 3D neural networks stimulated from the bottom layer, there was a high variability of the t60 and such parameter shows an almost uniform distribution within an interval of 100–1,200 ms (Figure 7e). Finally, in the case of 3D networks stimulated from the top layer, the responses to stimulation were very much delayed (Figure 7c) as the recorded evoked responses (related to neurons in the read-out layer) needed to be transmitted to such bottom layer with the possible involvement of several neurons and reverberating circuits. The t60 time values distribute in an interval ranging from 500 ms to 1,400 ms (Figure 7f). The cut-off value observed around 500 ms might indicate that only very few poly-synaptic pathways or direct functional connections crossed this culture in the z-direction as the 60% of the total responses reached the MEA substrate after such a long time delay. The electrophysiological specificity of the analyzed 3D networks was further demonstrated by the analysis and comparison, in all the performed experiments, of the t60 and t90 (time delay to have the 90% of the response to the stimulation) (Figure 7g). Time values are reported for 2D and 3D networks stimulated from the bottom layer (P-value = 9·10−4, Mann-Whitney U-test) and for 3D networks stimulated from the top layer (P-value = 2·10−4, Mann-Whitney U-test).
2D and 3D neural network response to electrical stimulation.
Raw data showing the response of a sample electrode to stimulation (red bar) in case of: (a). 2D neural network; (b). 3D neural network stimulated from the bottom layer; (c). 3D neural network stimulated from the top layer. Time instants in which the 60% of the PSTH area occurs for all the recording channels in case of: (d). 2D neural network; (e) 3D neural network stimulated from the bottom layer; (f). 3D neural network stimulated from the top layer. (g). Time occurring to generate 60% and 90% of response to stimulation for 2D and 3D networks. Asterisks above the plot indicate significant differences (P-value = 9·10−4 and P-value = 2·10−4, Mann-Whitney U-test). (h). Percentage of PSTH area values evaluated within different temporal windows.
2D networks displayed a reliable response time (also qualitatively found in previous works26,27) in which the 60% of the PSTH area occurred within the first 200 ms. The values detected for the 3D networks were higher and more variable. In the case of the bottom layer stimulation, the t60 value was 680 ms ± 28 ms and in the case of the top layer stimulation, the t60 shifted to 1,050 ms ± 38 ms. The time in which we found the 90% of the total evoked responses to stimulation (t90) was obviously higher than t60, but it followed the same trend (Figure 7g).
Moreover, we evaluated the percentage of the PSTH area generated after electrical stimulation in different time windows (Figure 7h) to quantify the different response modes of the measured networks. The response to stimulation of 2D networks was very fast: about 90% of the PSTH area was reached within the first 500 ms. 3D neural networks stimulated from the bottom layer exhibited a similar response to stimulation within all the time windows: it can be observes a fast response (35% of PSTH area reached within the first 100 ms) and also a slow response (about 30% of the response to stimulation was detected between 1 s and 2 s). In the case of 3D networks stimulated from the top layer, the fast response was not detected (only about 10% of PSTH area was within the first 300 ms) suggesting that no detectable direct pathway was present. The responses generated from this type of stimulation were slow: about 90% of the PSTH area was reached between 500 ms and 2 s.
As a final control, to prove that evoked responses recorded in the read-out layer when stimulating from the top, were due to synaptic transmission, we performed specific experiments by blocking synaptic transmission. We administered a cocktail of bicuculline (BIC, 25 μM), 2-amino-5-phosphonovalerate (APV, 50 μM), 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, 50 μM)24 after a first phase of repeated stimulation (control condition) of the analyzed 3D network. Before the synaptic blockade, the top layer stimulation indeed generated a response of the network (see Supplementary - Fig. S4). When we administered the synaptic blockade to the culture, we did not find any evoked response (see Supplementary - Fig. S4b–c). This result indicates that the response detected at the bottom layer was due to the synaptic transmission among different neurons that eventually found a target neuron coupled to the planar MEA in the read-out layer. Thus, the evoked response was due to synaptic reverberation and amplification and not to purely neuritic propagation meaning that direct connections from top layer to the surface of the MEA are unlikely. That is also somehow intrinsically due to the experimental procedure for the 3D network construction in which the bottom layer is first coupled to the planar MEA and then assembled with the upper layers.
Discussion
We presented a new experimental in-vitro platform constituted of 3D engineered neuronal cultures coupled to MEAs for network electrophysiology.
The use of microbead scaffolds was specifically optimized and tailored to be integrated with planar MEA in order to investigate the functional properties (i.e. electrical activity) of 3D hippocampal networks that were never presented before. We carefully compared the spontaneous and evoked electrophysiological activity of 3D cultures with the traditional network dynamics from homogeneous-uniform 2D cultures. First, in the developed 3D engineered hippocampal assemblies, cell morphology, connectivity (see also Figure 2) and, potentially, extracellular matrix, are much closer to the in-vivo situation1,4,28. Second, we observed striking differences with respect to uniform 2D networks and we quantified evidences of a wide dynamic repertoire of activity patterns possibly recapitulating various activity dynamics of in-vivo brain regions29,30. Quasi-synchronous network bursting activity of high density 2D neuronal networks9,18,31,32 was maintained in 3D cultures but global frequency was decreased (<1 Hz) and global synchrony was lost (spatial segregation of bursting - see Figure 3). Even if the recorded dynamics were very different, the average connectivity (i.e., 600 connections per neuron) was found to be the same in both 2D and 3D networks and the proportion between GABAergic and glutammatergic populations was likely to remain similar in both 2D and 3D models (with about a 1:5 ratio, see also Supplementary – Fig. S5 a–b)24,33,34. In the 3D architecture, we can speculate that, with the enhanced dendritic development, the resulting network was more complex and that cell morphology might also contribute to such increased complexity. We can hypothesize that the different GABAergic interneuron populations could gain a considerable increase of the functional surface (volume) compared to those grown in the 2D cultures. These possible wider and longer interactions with other neurons could contribute to desynchronize and temporally differentiate the network activity, hence producing bursting activities confined to sub-populations and global asynchronous activity patterns35. The addition of BIC induced in the 3D network model a more synchronized state (similar to what happen in uniform 2D networks), indicating a possible more synchronized activity in the upper layers and thus determining a reduced impact of the electrophysiological signals coming from above (see Supplementary – Fig. S2).
Along this direction, a systematic study of the spontaneous activity of 3D networks during development with the specific labeling of interneurons, could contribute to the understanding of the significance of the balance between excitation and inhibition with specific reference to the role of GABAergic populations35,36,37, distribution of hubs38 and network synchronization39.
Although such variable spontaneous activity together with the analysis of signal propagation is a convincing hallmark of the inherent contribution of the 3D structure to the network dynamics, the ultimate evidence that we are playing with actual 3D functionally interconnected neuronal networks is given by the results obtained upon the application of an external electrical stimulation.
2D interconnected networks stimulated by different electrodes, showed a relatively fast and synchronized response depending on the stimulating site. The site of stimulation causes an almost uniform response (for the high-connectivity of the network) in all the active sites (see Supplementary – Fig. S6a–b). The response time is relatively fast and confined below the first 250 ms (Figure 7d). 3D networks stimulated from the bottom layer exhibit various types of synchronized response (see also Supplementary – Fig. S6c–d) often generating a uniformly distributed response delay (Figure 7e). In general, the evoked activity can be thought as the combination of two types of response. The first type is generated by subsets of neurons in the read-out layer that are connected with subgroups of neurons in the same layer. The second type of response is generated by subsets of neurons in the read-out layer connected with sub-networks of neurons in the upper layers. The first type of response is fast; the second type is slow. Because of the different described types of activated circuits, the network response is not globally synchronized. When stimulating 3D networks from the top layer, the stimulation needs to be transmitted, through different neurons of the various layers, to neurons of the read-out layer coupled to the MEA generating time delays greater than 500 ms (cf. Figure 7f). These long delays could be explained by a less effective connectivity in the z-direction and by a possible decrease in the synaptic density from the bottom to the top layer. The administration of synaptic blockers to the culture impairs the recording of evoked responses in the bottom layer, thus demonstrating that activity propagates through synaptic reverberation and amplification in the different layers. The enhanced variability in the time delays of the evoked responses (cf. Figure 7h) is an additional proof we are facing heterogeneous functionally interconnected 3D cultured networks.
In summary, the developed experimental paradigm can constitute the basis for a next class of experimental models to study neurophysiology in in-vitro systems, for investigating the computational properties of neuronal networks and for developing new bio-hybrid microsystems.
Methods
Cell culture
Hippocampal neurons were dissociated from E18 Sprague Dawley rats (Charles River Laboratories, Milano). The procedure was approved by the European Animal Care Legislation and by the guidelines of the University of Genova. The day before the plating, MEAs (Multi Channel System MCS GmbH) were sterilized at 120°C in the oven and the microbeads were sterilized with ethanol at 70% for 1–2 hours. The sterilized material was therefore exposed to the coating treatment with adhesion protein Laminin (L-2020 Sigma) and Poli-Lysin (P-6407 Sigma) at 0.05 μg/ml overnight in incubator at 37°C. The adhesion factors were removed and the treated glass surfaces washed with sterile water. MEAs were left to dry inside the laminar hood. Lastly, the PDMS mask (Corning Sigma) was put on the electrodes area. From each embryo, hippocampi were removed and placed into ice cold Hank's balanced salt solution. The tissue was then dissociated in 0.125% of Trypsin/Hank's solution containing 0.05% of DNAse (D-5025 Sigma-Aldrich) for 15–18 min at 37°C. The supernatant solution was removed and the enzymatic digestion was stopped by adding 10% fetal bovine serum (FBS) in Neurobasal medium for 5 min. Medium with FBS was removed and replaced with Neurobasal medium supplemented with B27, 1% Glutamax, gentamicin 10 μg/ml (Gibco Invitrogen). Some cells were then plated directly onto the area of MEA electrodes, defined by the PDMS mask, while some others were distributed onto the microbead monolayer inside the Transwell® supports (Costar Sigma) to create the 3D assembly. The obtained 2D and 3D cultures were maintained in a humidified CO2 atmosphere at 37°C for 4–5 weeks. Half of the media was replaced once a week. No antimitotic drug was added to prevent glia proliferation, since glial cells are essential elements for a healthy development of neuronal networks.
Glass microbeads
Glass microbeads (distributed by Distrilab-Duke Scientific) were used as scaffold to create 3D neuronal networks. The cell density and the thickness of the reconstructed tissue can be tuned depending on the diameters of the sphere and the number of transferred layers. Glass microbeads with diameter of 40 μm (certified mean diameter of 42.3 ± 1.1 μm) were used and 5 to 8 layers were stacked.
Immunocytochemistry
Hippocampal cultures were fixed in 4% paraformaldehyde in Phosphate Buffer solution (PBS), pH 7.4 for 30 min at room temperature. Permeabilization was achieved with PBS containing 0.5% Triton-X100 for 15 min at room temperature and non-specific binding of antibodies was blocked with an incubation of 45 min in a blocking buffer solution consisted of PBS, 3% BSA (bovine serum albumin Sigma) and 0.5% FBS. Cultures were incubated with primary antibody diluted in PBS Blocking buffer for 2 hours at room temperature or incubated at 4°C overnight in a humidified atmosphere. Cultures were rinsed three times with PBS and finally exposed to the secondary antibodies: Alexa Fluor 488 or Alexa Fluor 546 Goat anti mouse or Goat anti rabbit, diluted respectively 1:700 and 1:1,000 (Invitrogen Life Technologies S. Donato Milanese). The antibodies used in the images are in the following order: MAP-2 1:500 (Chemicon Millipore), NeuN 1:400 (Chemicon Millipore), GABA 1:700 (Sigma), Synapsin 1:200 (Chemicon Millipore), Dapi 300 nM (Sigma). To verify the presence of glial cells in the culture, we fixed and exposed to the marker GFAP (monoclonal or polyclonal antibodies Sigma) both 2D controls (on glass and on MEA) and 3D samples assembled on coverslips or onto MEA. The evaluation of the samples was performed by confocal-laser scanning microscopy, widefield epifluorescence microscope Olympus IX-70 inverted (Fig. 2a) and Olympus BX-51 upright microscope (Fig. 2b). Image acquisition with Olympus was done with a Hamamatsu Orca ER II digital cooled CCD camera driven by Image ProPlus software (Media Cybernetic).
Optical setup
Confocal imaging was acquired on two different microscopes: a Leica TCS SP5 AOBS Tandem DMI6000 inverted microscope using a HCX PL APO 63× N.A. 1.40-0.60 Oil objective (Leica Microsystems, Mannheim, Germany) and a Nikon A1 Confocal inverted microscope equipped with CF1Plan Apocr λ 20 x W.D.1 mm A.N.0.75 (Nikon Instruments Europe B.V, Amsterdam).
2PE imaging was performed using a fs-pulsed Ti: sapphire laser Chameleon Ultra (Coherent, Santa Clara, CA, USA) coupled with Leica TCS SP5 AOBS Tandem DM6000 upright microscope equipped with HCX APO 20× N.A. 0.50 WI objective and HCX APO L 40× N.A. 0.80 WI objective (Leica Microsystems, Mannheim, Germany). Data were analyzed by means of the LAS AF V.2.6 software (Leica Microsystems, Mannheim, Germany), Nis elements V4.0 (Nikon Instruments Europe B.V, Amsterdam), ImageJ (National Institutes of Health, USA) and SVI Huygens Professional for volume rendering.
Data analysis
Data analysis was performed off-line by using a custom software package named SPYCODE40 developed in MATLAB (The Mathworks, Natick, MA, USA). Spike detection. Extracellularly recorded spikes were detected using the PTSD (Precise Timing Spike Detection) algorithm41. Briefly, spike trains were built using three parameters: (1) a differential threshold set to 8 times the standard deviation of the baseline noise independently for each channel; (2) a peak lifetime period (set at 2 ms); (3) a refractory period (set at 1 ms). The data presented in the text were not spike sorted. This choice was made according to the fact that, both in 2D and 3D networks, during a burst a global increase of the activity produces a fast sequence of spikes with different and overlapping shapes which make the sorting difficult and unreliable42. Burst detection. Bursts were identified according to the method described in Pasquale et al.40. The algorithm is based on the computation of the logarithmic inter-spike interval histogram in which inter-burst activity (i.e., between bursts and/or outside bursts) and intra-burst activity (i.e., within burst) for each recording channel can be easily identified and then, a threshold for detecting spikes belonging to the same burst is automatically defined. Network burst detection. A similar procedure was followed for the detection of network bursts, looking for sequences of closely-spaced single-channels bursts. A network burst is identified if it involves at least the 80% of the network active channels40. Instantaneous Firing Rate (IFR). The IFR is computed by dividing the number of spikes which falls in a small sliding window by the window length. Such a window was implemented using a Gaussian kernel (100 ms width). The mean firing rate (MFR) of the network was obtained by computing the firing rate of each channel averaged among all the active electrodes of the MEA (i.e, being an active electrode defined by an activity > 0.1 spike/s). Peri or Post Stimulus Time Histogram (PSTH). The PSTH was calculated by considering 2 s time windows from the recordings that follow each stimulus. First, each time window was divided into 10 ms bins and then the number of spikes occurring in each time bin was counted. Finally, the histograms of each channel were normalized over the number of stimuli (50), the bin size and the maximum number of evoked spikes in a bin for each experiment (culture). Cross-correlation. The level of synchronization among multi-unit recordings was estimated by the cross-correlation function43. Given two spike trains (e.g., X and Y) recorded from two electrodes of the MEA, we counted the number of events in the Y train within a time frame around the X event of ±1 s, by using bins of 5 ms. The cross-correlogram coefficient, C(0), represents the area of the cross-correlogram in the central bin and it was evaluated to quantify the synchronization level among the recording channels. We defined an arbitrary threshold as <C(0)> + 2 std(C(0)) to detect the most synchronized electrodes. To quantify the correlation level the CPeak value was computed as the value of the cross-correlogram in an area around the maximum detected peak. C(0) and Cpeak values are normalized with respect to the auto-correlation value. Statistics. Unless otherwise stated, data were expressed as mean ± standard error of the mean. Statistical analysis was performed using MATLAB (The Mathworks, Natick, MA, USA). Since data do not follow a normal distribution (evaluated by the Kolmogorov-Smirnov normality test), we performed a non-parametric Mann-Whitney U-test. Significance levels were set at p < 0.001.
MEA set-up
The electrophysiological activity was recorded for 30 min by means of Micro-Electrode Arrays (MEAs) made up of 60 planar microelectrodes (TiN/SiN, 30 μm electrode diameter, 200 μm spaced) arranged over an 8 × 8 square grid (except the four electrodes at the corners), supplied by Multi Channel Systems (MCS, Reutlingen, Germany). After 1200× amplification (MEA 1060, MCS), signals were sampled at 50 kHz using the MCS data acquisition card. Recordings were performed outside the incubator at temperature of 37°C; to prevent evaporation and changes of the pH medium, a constant slow flow of humidified gas (5% CO2, 20% O2, 75% N2) was inflated onto the MEA. Electrical stimuli were delivered by using a commercial general-purpose stimulus generator (STG 1008, MCS), which supplies current and voltage pulses to be applied to selected electrodes of the MEA (bottom stimulation), or to a borosilicate glass micropipette (estimated impedance of 0.9 MΩ). A tungsten coil (Concentric Bipolar Electrode, World Precision Instruments) was then inserted into the micropipette and connected to the stimulus generator (top stimulation). Stimuli were sent from the electrode at frequency of 0.2 Hz for 5 min with amplitude of 1.5 V (bottom stimulation) and 3 V (top stimulation) peak-to-peak. The stimulus pulse was biphasic (positive first) and lasted for 500 μs with a 50% duty cycle.
References
Cullen, D. K., Wolf, J. A., Vernekar, V. N., Vukasinovic, J. & LaPlaca, M. C. Neural tissue engineering and biohybridized microsystems for neurobiological investigation in vitro (Part 1). Crit. Rev. Biomed. Eng. 39, 201–240 (2011).
Lee, J., Cuddihy, M. J. & Kotov, N. A. Three-dimensional cell culture matrices: state of the art. Tissue Eng. B Rev. 14, 61–86 (2008).
Kunze, A., Giugliano, M., Valero, A. & Renaud, P. Micropatterning neural cell cultures in 3D with a multi-layered scaffold. Biomaterials 32, 2088–2098 (2011).
Irons, H. R. et al. Three-dimensional neural constructs: a novel platform for neurophysiological investigation. J. Neural. Eng. 5, 333–341 (2008).
Rowe, L. et al. Active 3-D microscaffold system with fluid perfusion for culturing in vitro neuronal networks. Lab Chip 7, 475–482 (2007).
Gross, G. W., Williams, A. N. & Lucas, J. H. Recording of spontaneous activity with photoetched microelectrode surfaces from mouse spinal neurons in culture. J. Neurosci. Meth. 5, 13–22 (1982).
Gal, A. et al. Dynamics of excitability over extended timescales in cultured cortical neurons. J. Neurosci. 30, 16332–16342 (2010).
Shahaf, G. & Marom, S. Learning in networks of cortical neurons. J. Neurosci. 21, 8782–8788 (2001).
Eytan, D. & Marom, S. Dynamics and effective topology underlying synchronization in networks of cortical neurons. J. Neurosci. 26, 8465–8476 (2006).
Dranias, M. R., Ju, H., Rajaram, E. & VanDongen, A. M. Short-term memory in networks of dissociated cortical neurons. J. Neurosci. 33, 1940–1953 (2013).
Wagenaar, D. A., Madhavan, R., Pine, J. & Potter, S. M. Controlling bursting in cortical cultures with closed-loop multi-electrode stimulation. J. Neurosci. 25, 680–688 (2005).
Pautot, S., Wyart, C. & Isacoff, E. Y. Colloid-guided assembly of oriented 3D neuronal networks. Nat. Meth. 5, 735–740 (2008).
Berdondini, L. et al. Active pixel sensor array for high spatio-temporal resolution electrophysiological recordings from single cell to large scale neuronal networks. Lab Chip 9, 2644–2651 (2009).
Frey, U., Egert, U., Heer, F., Hafizovic, S. & Hierlemann, A. Microelectronic system for high-resolution mapping of extracellular electric fields applied to brain slices. Biosens. Bioelectron. 24, 2191–2198 (2009).
Schuz, A. & Palm, G. Density of neurons and synapses in the cerebral cortex of the mouse. J. Comp. Neurol. 286, 442–455 (1989).
Brewer, G. J., Boehler, M. D., Jones, T. T. & Wheeler, B. C. NbActiv4 medium improvement to Neurobasal/B27 increases neuron synapse densities and network spike rates on multielectrode arrays. J. Neurosci. Meth. 170, 181–187 (2008).
Cullen, D. K., Gilroy, M. E., Irons, H. R. & Laplaca, M. C. Synapse-to-neuron ratio is inversely related to neuronal density in mature neuronal cultures. Brain Res. 1359, 44–55 (2010).
Gandolfo, M., Maccione, A., Tedesco, M., Martinoia, S. & Berdondini, L. Tracking burst patterns in hippocampal cultures with high-density CMOS-MEAs. J. Neural. Eng. 7, 056001 (2010).
Wang, L., Riss, M., Buitrago, J. O. & Claverol-Tinture, E. Biophysics of microchannel-enabled neuron-electrode interfaces. J. Neural. Eng. 9, 026010 (2012).
Leondopulos, S. S., Boehler, M. D., Wheeler, B. C. & Brewer, G. J. Chronic stimulation of cultured neuronal networks boosts low-frequency oscillatory activity at theta and gamma with spikes phase-locked to gamma frequencies. J. Neural. Eng. 9, 026015 (2013).
Orlandi, J. G., Soriano, J., Alvarez-Lacalle, E., Teller, S. & Casademunt, J. Noise focusing and the emergence of coherent activity in neuronal cultures. Nature Phys. 9, 582–590 (2013).
Ham, M. I., Bettencourt, L. M., McDaniel, F. D. & Gross, G. W. Spontaneous coordinated activity in cultured networks: analysis of multiple ignition sites, primary circuits and burst phase delay distributions. J. Comput. Neurosci. 24, 346–357 (2008).
Tscherter, A., Heuschkel, M. O., Renaud, P. & Streit, J. Spatiotemporal characterization of rhythmic activity in rat spinal cord slice cultures. Eur. J. Neurosci. 14, 179–190 (2001).
Bonifazi, P., Ruaro, M. E. & Torre, V. Statistical properties of information processing in neuronal networks. Eur. J. Neurosci. 22, 2953–2964 (2005).
Ruaro, M. E., Bonifazi, P. & Torre, V. Toward the neurocomputer: image processing and pattern recognition with neuronal cultures. IEEE Trans. Biomed. Eng. 52, 371–383 (2005).
Chiappalone, M., Massobrio, P. & Martinoia, S. Network plasticity in cortical assemblies. Eur. J. Neurosci. 28, 221–237 (2008).
Jimbo, Y., Tateno, T. & Robinson, H. P. Simultaneous induction of pathway-specific potentiation and depression in networks of cortical neurons. Biophys. J. 76, 670–678 (1999).
Edelman, D. B. & Keefer, E. W. A cultural renaissance: in vitro cell biology embraces three-dimensional context. Exp. Neurol. 192, 1–6 (2005).
Klausberger, T. et al. Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature 421, 844–848 (2003).
Leinekugel, X. et al. Correlated bursts of activity in the neonatal hippocampus in vivo. Science 296, 2049–2052 (2002).
Wagenaar, D. A., Pine, J. & Potter, S. M. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 7, 11 (2006).
Chiappalone, M., Bove, M., Vato, A., Tedesco, M. & Martinoia, S. Dissociated cortical networks show spontaneously correlated activity patterns during in vitro development. Brain Res. 1093, 41–53 (2006).
Marom, S. & Shahaf, G. Development, learning and memory in large random networks of cortical neurons: lessons beyond anatomy. Quart. Rev. Biophys. 35, 63–87 (2002).
Benson, D. L., Watkins, F. H., Steward, O. & Banker, G. Characterization of GABAergic neurons in hippocampal cell cultures. J. Neurocytol. 23, 279–295 (1994).
Baltz, T., de Lima, A. D. & Voigt, T. Contribution of GABAergic interneurons to the development of spontaneous activity patterns in cultured neocortical networks. Front. Cell. Neurosci. 4, 15 (2010).
Klausberger, T. GABAergic interneurons targeting dendrites of pyramidal cells in the CA1 area of the hippocampus. Eur. J. Neurosci. 30, 947–957 (2009).
Voigt, T., Opitz, T. & de Lima, A. D. Activation of early silent synapses by spontaneous synchronous network activity limits the range of neocortical connections. J. Neurosci. 25, 4605–4615 (2005).
Bonifazi, P. et al. GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424 (2009).
Picardo, M. A. et al. Pioneer GABA cells comprise a subpopulation of hub neurons in the developing hippocampus. Neuron 71, 695–709 (2011).
Bologna, L. L. et al. Investigating neuronal activity by SPYCODE multi-channel data analyzer. Neural Net. 23, 685–697 (2010).
Maccione, A. et al. A novel algorithm for precise identification of spikes in extracellularly recorded neuronal signals. J. Neurosci. Meth. 177, 241–249 (2009).
Wagenaar, D. A., Nadasdy, Z. & Potter, S. M. Persistent dynamic attractors in activity patterns of cultured neuronal networks. Phys. Rev. E 73, 051907 (2006).
Garofalo, M., Nieus, T., Massobrio, P. & Martinoia, S. Evaluation of the performance of information theory-based methods and cross-correlation to estimate the functional connectivity in cortical networks. PLoS ONE 4, e6482 (2009).
Acknowledgements
The authors thank Giorgio Carlini for the technical support in developing the confinement structure and Mauro Frega for the technical assistance in preparing the movies. The authors also wish to thank Dr. Michela Chiappalone and Dr. Valentina Pasquale for their valuable comments on this work. The research leading to these results has received funding from the European Union's Seventh Framework Programme (ICT-FET FP7/2007-2013, FET Young Explorers scheme) under grant agreement n° 284772 (BrainBow).
Author information
Authors and Affiliations
Contributions
S.M., P.M., M.F., M.T. conceived and designed the study. M.T. prepared the cultures and conducted the immunofluorescence staining, M.P. performed the imaging characterization. M.F. and M.T. collected the data. M.F. analyzed the data. P.M., M.F., M.T. and S.M. discussed the results and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Supplementary Information
Supplementary Movie 1
Supplementary Information
Supplementary Movie 2
Supplementary Information
Supplementary Movie 3
Supplementary Information
Supplementary Movie 4
Supplementary Information
Supplementary Movie 5
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Frega, M., Tedesco, M., Massobrio, P. et al. Network dynamics of 3D engineered neuronal cultures: a new experimental model for in-vitro electrophysiology. Sci Rep 4, 5489 (2014). https://doi.org/10.1038/srep05489
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05489
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.