Abstract
The field of conventional energy conversion using radioisotopes has almost exclusively focused on solid-state materials. Herein, we demonstrate that liquids can be an excellent media for effective energy conversion from radioisotopes. We also show that free radicals in liquid, which are continuously generated by beta radiation, can be utilized for electrical energy generation. Under beta radiation, surface plasmon obtained by the metallic nanoporous structures on TiO2 enhanced the radiolytic conversion via the efficient energy transfer between plasmons and free radicals. This work introduces a new route for the development of next-generation power sources.
Similar content being viewed by others
Introduction
Particles emitted from radioisotopes can be used to convert the radiant energy into electricity. Radioisotope energy conversion for power generation has been intensively studied to develop power sources for wide range of applications, from energizing cardiac pacemakers in human body1 to challenging outer planet missions2. As compared to various indirect conversion methods, which collect electricity from the secondary energy forms of heat or light generated by radiation3,4, direct conversion methods produce electric power straight from energetic particles5,6. Beta particles can produce electron-hole pairs in semiconductors via their loss of kinetic energy and can contribute to the generation of electric power6. Although potential applicability of radioisotopes in portable power sources that do not require recharging seems very attractive7, it has been reported that only a small portion of the entire radiation energy can be converted into electrical energy5,6,7,8,9,10. Moreover, most betavoltaic cells suffer from serious radiation damage to the lattice structures of semiconductors and subsequent performance degradation due to the high kinetic energy of the beta particles11. Alternatively, to minimise lattice damage in semiconductors, wide band gap materials are typically used. However, radiation-resistive materials, such as SiC and GaN, still show very low energy conversion efficiencies12,13. Little improvement has been made even after vigorous research on various improvement methods utilizing porous structures14, inverted pyramidal cavities15 and three dimensional silicon pillar structures15 to increase rectifying junction areas. Although, thus far, there is no method for completely avoiding radiation damage to semiconductors, the use of a liquid-phase semiconductor material has been introduced as a possible means to overcome the radiation damage and structural defect problem16. One major benefit of utilising a liquid-phase material is the well-known ability to efficiently absorb the kinetic energy of beta particles17.
Since the advent of nuclear power, liquids have been intensively studied for use as a radiation-shielding material. Large amounts of radiation energy can be absorbed by water. When radiation energy is absorbed by an aqueous solution, free radicals (e.g., eaq−, ·OH, H·, HO2·) can be produced through radiolytic interactions18,19,20. These free radicals are known to affect the generation of molecular by-products, such as H2O2 and H221,22,23,24. However, counterintuitively, the generation of electricity from a solution containing an ample amount of absorbed radiation energy has not yet been vigorously studied. Here, we demonstrate a new method for the generation of electricity using a device that separates the radiolytic current from the free radicals by splitting the water.
Results
Design and operating principle of Pt/nanoporous TiO2 radiolytic cell
Our water splitter is composed of a nanoporous semiconductor coated with a thin Pt film to produce a specially designed metal-semiconductor junction (Fig. 1a). As a suitable semiconductor material for water decomposition, we used a very stable and common large band gap oxide material, TiO2, because the use of large band gap oxide materials as a semiconducting catalyst can improve the radiolysis yield25,26,27. Nanoporous TiO2 was formed by anodising and subsequently thermally oxidising a thin Ti film. The large surface area of the porous structure can provide more chemical reaction sites than a planar surface. To form a stable Schottky contact at the semiconductor/metal interface, a thin Pt film was uniformly deposited using a radio frequency (RF) sputtering system. As shown in the band diagram of the junctions in Fig. 1b, a Schottky barrier of 0.45 eV is formed because the Fermi energy (EF) of TiO2, an n-type semiconducting oxide, is 5.2 eV28,29 while that of Pt is 5.65 eV30 with respect to the vacuum level. To experimentally confirm the Schottky barrier height between Pt and TiO2, we performed XPS analysis and measured the Schottky barrier height of 0.6 eV between Pt and Pt/TiO2 layers. When high-energy beta radiation passes through Pt and nanoporous TiO2, electron-hole pairs are produced inside the nanoporous TiO2. In particular, the holes generated in TiO2 move toward the Pt/liquid interface and then react with redox couples of water molecules, while the electrons are transported through the nanoporous TiO2 to the other electric contact due to the built-in potential at the Pt/electrolyte interface. In general, TiO2 is resistant to corrosion, but the additional layer of Pt can further protect the TiO2 layer under the harsh conditions of high pH values that are needed for water splitting. In addition, the porosity of the TiO2 leads to myriad nanoholes in the Pt film, which create localised surface plasmons that act as harmonic oscillators in response to an oscillating external electric field. Since the first report31 of the generation of surface plasmons on rough metal surfaces by electron illumination in 1977, many studies have examined various metal structures32,33,34,35. Surface plasmons excited on the Pt surface can produce electron–hole pairs, with the excited electrons transiently occupying normally empty states in the Pt conduction band above the Fermi energy level. Most of the excited electrons are sufficiently energetic to enter the conduction band of TiO2.
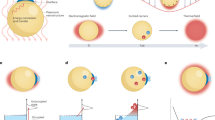
Structure and mechanism of the plasmon-assisted radiolytic water splitter.
(a), Cross-sectional schematic illustration of nanoporous TiO2 prepared by anodising and thermally oxidising a thin Ti film deposited on a glass substrate. The thin Pt film is deposited on top of the TiO2 nanopores using an RF sputtering system. (b), Energy level diagram of a surface-plasmon-assisted radiolytic water splitter. CB, conduction band; VB, valence band; EF, Fermi energy; eaq−, aqueous electron; ·OH, hydroxyl free radical; β, beta radiation.
In contrast to photocatalytic cells, high-energy beta radiation in our device can produce free radicals in water through the loss of kinetic energy. In a meta-stable state, the free radicals are recombined into water molecules or trapped in water molecules36,37,38. Thus, the free radicals produced by the radiation can be converted into electricity by a plasmon-assisted, wide band gap oxide semiconducting material using a water splitting technique at room temperature.
Structural properties of radiolytic electrode
Scanning electron microscopy (SEM) images and X-ray diffraction (XRD) data for the nanoporous TiO2 are shown in Fig. 2. The cross-sectional SEM image shows the existence of nanopores 100 nm in diameter and 1 μm deep with a spacing of 100 nm (Fig. 2a). Figure 2b shows a top-viewed SEM image of a 50-nm-thick Pt film coated surface of nanoporous TiO2. After Pt deposition on nanoporous TiO2 film, the size of Pt nanoholes turns out to be approximately 10 ~ 20 nm (Fig. 2b, inset). The density of holes is 3 ~ 5 × 109 cm−2. As shown by the XRD data in Fig. 2c, after the as-deposited Ti was anodised for 5 min, the intensity of the Ti (002) peak decreased compared to that of the Ti (001) peak, indicating the presence of vertically arranged uniform nanopores along the <002> direction of the Ti. After the anodised Ti was thermally oxidised at 450°C for 2 hours, the (001) and (002) peaks of Ti disappeared and a new peak (37.24°) corresponding to the rutile crystalline structure appeared, indicating that TiO2 has a band gap of 3.2 eV39.
Electrical properties of radiolytic cell
Illustrations and photographs of the test setup and of the Pt/nanoporous TiO2 cathode are shown in Figs. 3a and b, respectively. During our experiment, gas bubbles on the PET plastic shielding film of the Sr-90/Y-90 source (Fig. 3a) clearly demonstrated the occurrence of water splitting. To evaluate the radiolytic performance of the Pt/nanoporous TiO2 electrode in a 1 M KOH aqueous solution, we employed a potentiostat. We measured the current density-voltage characteristics (Fig. 3c), open circuit voltage and the current density at 0 V, −0.1 V, −0.4 V, −0.7 V and −0.9 V for 1200 seconds each under continuous irradiation (Fig. S2). Figure 3c shows the current density - voltage (J-V) characteristics for the Pt/nanoporous TiO2 radiolytic electrode (red line) under irradiation. For comparison, we measured the radio current of a nanoporous TiO2 electrode (blue line) under irradiation and the dark current of Pt/nanoporous TiO2 (black line) under no irradiation. While the radio current of nanoporous TiO2 is slightly larger than the dark current of Pt/nanoporous TiO2, the radio current of Pt/nanoporous TiO2 is significantly larger than both the radio current of nanoporous TiO2 and the dark current of Pt/nanoporous TiO2. The radio current density of Pt/nanoporous TiO2 is saturated at −175.4 μA/cm2 for 0 V, while the dark current density of Pt/nanoporous TiO2 and the radio current density of TiO2 are approximately −1.051 μA/cm2 and −0.0719 μA/cm2, respectively. At −0.9 V, the radio current density of Pt/nanoporous TiO2, the dark-current density of Pt/nanoporous TiO2 and the radio current density of TiO2 are −83.336 μA/cm2, 70.31 μA/cm2 and 2.85 μA/cm2, respectively. These measurement data are summarized and reshaped into Table S1 to compare the performance of the irradiated devices with Pt/nanoporous TiO2 and nanoporous TiO2. Figure 3d manifests the clear difference in output power from devices with and without the plasmonic Pt layer. The output power densities (11.59 μW/cm2 at −0.1 V and 75.02 μW/cm2 at −0.9 V) of the Pt/nanoporous TiO2 electrode are higher than the power densities (−0.0027 μW/cm2 at −0.1 V and −2.565 μW/cm2 at −0.9 V) of nanoporous TiO2. For a radioactive material activity of 15 mCi (±10%), the total number of beta particles per unit time is estimated to be 5.55 × 108 s−1 and the total input power density of the beta particles is 139.238 μW/cm2, when the average kinetic energy of Sr-90/Y-90 is 490.96 keV. From this data, maximum energy conversion efficiency (η) of our device was approximately estimated to be 53.88% at −0.9 V using  , where Prad, Pchem and Pout are radiation power density of source (139.238 μW/cm2), chemical power density in water, and, output power density of device (75.02 μW/cm2), respectively. One possible reason for the high output power density under irradiation is that a certain level of the EHP ionisation energy of beta particles can easily excite electrons because the EHP ionisation energy is much higher than the band gap of each material while a large portion of the spectrum of solar light is below the TiO2 band gap, indicating that the TiO2 layer does not absorb sunlight well. Therefore, beta particles are a reliable energy source for electricity generation via water splitting.
, where Prad, Pchem and Pout are radiation power density of source (139.238 μW/cm2), chemical power density in water, and, output power density of device (75.02 μW/cm2), respectively. One possible reason for the high output power density under irradiation is that a certain level of the EHP ionisation energy of beta particles can easily excite electrons because the EHP ionisation energy is much higher than the band gap of each material while a large portion of the spectrum of solar light is below the TiO2 band gap, indicating that the TiO2 layer does not absorb sunlight well. Therefore, beta particles are a reliable energy source for electricity generation via water splitting.
Radio-current output at the Pt/nanoporous TiO2 electrode.
(a), Schematic view of the testing setup for Pt/nanoporous TiO2 under irradiation and a photograph of the Sr-90/Y-90 source with gas bubbles attached to the outer surface of the PET film. (b), Schematic diagram and photograph of the Pt/nanoporous TiO2 electrode. (c), J-V characteristics of irradiated devices with Pt/nanoporous TiO2 (red line) and nanoporous TiO2 (blue line) radiolytic electrodes and of unirradiated device with Pt/nanoporous TiO2 (black line) in a dark room. (d), Power densities of irradiated devices with Pt/nanoporous TiO2 (red bar) and nanoporous TiO2 (blue bar). The area of the electrode is 1 cm2.
Energy absorption of electron beam in the radiolytic cell using numerical simulation
To study the mechanism of the enhanced power conversion of beta radiation, we calculated the energy absorbed in an aqueous solution using Monte Carlo (MC) simulations40. The number of electrons utilised in this simulation was 10,000 and the kinetic energy of the electron beam was 546 keV. A beta particle is an electron, e−, or a positron, e+, that is generated when the neutron to proton ratio in the nucleus is too large, making the nucleus unstable41. In this simulation, the presence of secondary electrons generated by primary electrons was ignored and the electron beam was defined by a Gaussian distribution. The energy absorbed by the TiO2 film was calculated to be approximately 0.25% of the total energy of the electron beam (Fig. 4). In the middle of the water, the absorbed energy was approximately 55.57%. Note that the incident beta radiation can be scattered and reflected by our nanoporous structure, indicating that more energy will be absorbed by Pt/nanoporous TiO2 and water than expected in this simulation. Beta radiation can create vacancies in solids by primary knock-on atoms (PKA). For rutile TiO2, the threshold displacement energy is about 47 eV42. A required incident kinetic energy level of beta radiation for the vacancy production can be estimated from the displacement energy equation, Tm = 2(E + 2mc2)E/Mc2, where E is kinetic energy of beta radiation and c is speed of light. m and M are masses of electron and target atom, respectively. Figure S3 shows the relationship between the incident kinetic energy of beta radiation and the threshold displacement energy. Under beta radiation, the threshold displacement energy of 47 eV is equivalent to the incident kinetic energy of 271 keV for oxygen and 633.5 keV for titanium as shown in Fig. S3. We also found from MC simulations that the water can absorb beta radiation of 356 keV. Because the PKA damage in TiO2 occurs from the kinetic energy over 271 keV as shown in Fig. S3, the performance degradation of our radiolytic cell might begin with the kinetic energy over 627 keV. Although beta radiation from Sr-90/Y-90 includes higher energy beta particles than 627 keV as shown in Fig. S4, our radiolytic cell didn't show any performance degradation for about 6 hours (Fig. S2). Moreover, water can absorb 72.02% of the total kinetic energy in emission spectrum of Sr-90/Y-90. To determine the total kinetic energy passing through Pt/nanoporous TiO2, we considered the directional loss of radiation source. As shown in Fig. S5, the directional loss of our radiolytic cell is estimated to be approximately 54.88% and the amount of kinetic energy higher than 627 keV is only 12.62% of the total kinetic energy of beta radiation, indicating that performance degradation of our radiolytic cell may not be serious. Here, incident high-energy beta particles can excite electrons in the semiconductor via their energy loss, which is defined as the electron-hole pair (EHP) ionisation energy given by W± ≈ 2.8Eg + Eph, where Eg and Eph are the band gap and phonon energies (0.5 ≤ Eph ≤ 1 eV), respectively43. For TiO2, W± is approximately 9.46 eV. Because the high EHP ionisation energy is sufficient for tunnelling through a low Schottky barrier at the TiO2/liquid interface, the radio current of nanoporous TiO2 is lower than the radio current of Pt/nanoporous TiO2, as shown in Fig. 3c. When beta particles pass through the TiO2 layer (1 μm), the number of generated EHPs is estimated to be approximately 144 per single beta particle, that is, the deposition power is estimated to be 0.12 μW/cm2. Although most of the EHPs generated within the depletion region are separated due to the built-in potential of the thin TiO2 layer, the measured output power density was much less than the expected values of 75.02 μW/cm2 at −0.9 V. This result indicates that the EHPs generated in TiO2 via beta radiation are not sufficient to produce the total output power density measured in the experiment.
Generation and behaviour of free radicals under beta radiation
To understand the highly enhanced output power, it is necessary to understand the details of water radiolysis. High-energy electrons passing through an aqueous solution can ionise or excite water molecules, forming a number of transition species and stable products, as shown by the equation  , ·OH, H·, HO2·, H3O+, OH−, H2O2, H244. High levels of these products are formed by the absorption of 100 eV in the medium. The generated radicals are powerful redox reagents, i.e., eaq− is a strong reducing agent, H· is an equally strong reducing and oxidising agent and ·OH is a powerful oxidising agent. In water at high pH, eaq− and ·OH are produced in the largest quantities by the beta radiation. The standard potentials of eaq− and ·OH are E0 (H2O/eaq−) = −2.9 VNHE and E0 (·OH/H2O) = +2.7 VNHE, respectively45. These two species (eaq− and ·OH) react with water molecules during water radiolysis and then remain in the aqueous solution. They can then no longer react with each other or with surrounding water molecules. Once these two species (eaq− and ·OH) are solvated in an aqueous solution, they can be surrounded by water molecules in a meta-stable state for a few μs45,46. It is well known that water has a very large dielectric constant and consists of polar molecules, which prevent the electrostatic attraction between positive and negative charges and maintain the separated state of charges surrounded by oppositely charged ends of water dipoles. During the long lifetime of solvated electrons, beta radiation will continuously increase the number of solvated electrons in the water until they finally move to the surface of the water, where they are emitted as thermal energy. The floated electrons form the negatively charged surface of water47. Theoretically, water has lower standard potential (E0 (H2O/O2) = +0.82 VNHE and E0 (H2O/H2) = −0.41 VNHE) than free radicals, indicating that electrochemical energy of water is lower than that of free radicals. It was also reported that high electrochemical energy of solvated electrons (eaq−) can enable difficult chemical reactions to happen48. Moreover, the presence of an external electric field or electromagnetic field can release the solvated electrons from their confined environment of surrounding molecules49. This is because eaq− in water has very small diffusion efficiency (4.8 × 10−5 cm2/s) and electron mobility (1.84 × 10−3 cm2/V·s)50. Solvated electrons in water also need to get over the potential barrier of 0.2 ~ 0.5 eV set by the surrounding rigid water molecule network. Moreover, because water is located between both Pt electrodes (plasmonic layer and counter electrode), if same electrochemical reactions occur on both Pt surfaces, simply no current flow is expected.
, ·OH, H·, HO2·, H3O+, OH−, H2O2, H244. High levels of these products are formed by the absorption of 100 eV in the medium. The generated radicals are powerful redox reagents, i.e., eaq− is a strong reducing agent, H· is an equally strong reducing and oxidising agent and ·OH is a powerful oxidising agent. In water at high pH, eaq− and ·OH are produced in the largest quantities by the beta radiation. The standard potentials of eaq− and ·OH are E0 (H2O/eaq−) = −2.9 VNHE and E0 (·OH/H2O) = +2.7 VNHE, respectively45. These two species (eaq− and ·OH) react with water molecules during water radiolysis and then remain in the aqueous solution. They can then no longer react with each other or with surrounding water molecules. Once these two species (eaq− and ·OH) are solvated in an aqueous solution, they can be surrounded by water molecules in a meta-stable state for a few μs45,46. It is well known that water has a very large dielectric constant and consists of polar molecules, which prevent the electrostatic attraction between positive and negative charges and maintain the separated state of charges surrounded by oppositely charged ends of water dipoles. During the long lifetime of solvated electrons, beta radiation will continuously increase the number of solvated electrons in the water until they finally move to the surface of the water, where they are emitted as thermal energy. The floated electrons form the negatively charged surface of water47. Theoretically, water has lower standard potential (E0 (H2O/O2) = +0.82 VNHE and E0 (H2O/H2) = −0.41 VNHE) than free radicals, indicating that electrochemical energy of water is lower than that of free radicals. It was also reported that high electrochemical energy of solvated electrons (eaq−) can enable difficult chemical reactions to happen48. Moreover, the presence of an external electric field or electromagnetic field can release the solvated electrons from their confined environment of surrounding molecules49. This is because eaq− in water has very small diffusion efficiency (4.8 × 10−5 cm2/s) and electron mobility (1.84 × 10−3 cm2/V·s)50. Solvated electrons in water also need to get over the potential barrier of 0.2 ~ 0.5 eV set by the surrounding rigid water molecule network. Moreover, because water is located between both Pt electrodes (plasmonic layer and counter electrode), if same electrochemical reactions occur on both Pt surfaces, simply no current flow is expected.
FDTD simulations of Pt/nanoporous TiO2 on glass under an e-beam irradiation of 546 keV and optical measurement
One available external electric field in our device is the localised electric fields from the surface plasmons of the Pt nanoholes. To generate surface plasmons on the Pt/nanoporous TiO2 radiolytic electrode, we performed 3D-FDTD (finite-difference time-domain) numerical simulations using a commercially available FDTD code for simulating electron irradiation51. In FDTD, the macroscopic Maxwell equations are solved in discretised space and time to follow the response of a material to an applied electric field. For a numerical investigation of the beta radiation-excited photon emission in Pt/nanoporous TiO2, the electron beam can be modelled as a line current density source represented by  , where e is the electronic charge, v is the electron velocity, (x0, y0) represents the position of the focused electron beam, z is the direction of the electron velocity and ûz is the unit vector along the z direction. In the simulation, the current density was modelled as a series of dipoles with a temporal phase delay (z/v) related to the electron velocity, v (in this simulation, v = 0.875c, corresponding to the beta particle's kinetic energy of 546 keV used in the experiment and c is the velocity of light in free space). We conducted our simulations for three different points denoted 1–3 in the middle of a pore, at the side wall of a pore and between two pores, as depicted in Fig. 5a.
, where e is the electronic charge, v is the electron velocity, (x0, y0) represents the position of the focused electron beam, z is the direction of the electron velocity and ûz is the unit vector along the z direction. In the simulation, the current density was modelled as a series of dipoles with a temporal phase delay (z/v) related to the electron velocity, v (in this simulation, v = 0.875c, corresponding to the beta particle's kinetic energy of 546 keV used in the experiment and c is the velocity of light in free space). We conducted our simulations for three different points denoted 1–3 in the middle of a pore, at the side wall of a pore and between two pores, as depicted in Fig. 5a.
FDTD simulations of Pt/nanoporous TiO2 on glass under an e-beam irradiation of 546 keV and optical measurement.
(a), Cross-sectional view and top view for different e-beam positions marked as 1–3. In this simulation, d, s, t1 and t2 are 10 nm, 200 nm, 50 nm and 45 nm, respectively. (b), Emission spectra of the Pt/nanoporous TiO2 surfaces at positions 1–3. Arrows indicate the highest peak positions. Mark 4 shows the reflection of Pt/nanoporous TiO2 using an UV-VIS spectrometer. The same coloured dots indicate corresponding peaks of each spectrum. (c–d), Top and cross-sectional views of the near-field intensity distributions on Pt/nanoporous TiO2 at the top level of Pt nanohole at mark 1 for 290 nm. (e–f), Top and cross-sectional views of the near-field intensity distributions on Pt/nanoporous TiO2 at the top level of Pt nanohole at mark 2 for 287 nm. (g–h), Top and cross-sectional views of the near-field intensity distributions on Pt/nanoporous TiO2 at the top level of Pt nanohole at mark 3 for 377 nm. The field intensity is shown on a log scale, [E]2/[E0]2, where E and E0 are the generated and minimum electric field intensities, respectively.
To simulate the near-field electric intensities and emission spectra at the different positions, the induced electric field distributions were calculated by [E]2/[E0]2, where E and E0 are the generated and minimum electric field intensities, respectively, emitted normal and parallel to the Pt surface in the wavelength range of 200 to 700 nm. We investigated the near-field intensity distributions on Pt/nanoporous TiO2 at the different positions under focused electron irradiation using FDTD simulations. As shown in Fig. 5b, the highest emitted spectral peaks were calculated to occur at wavelengths of 293 nm, 517 nm and 376 nm when the electron irradiation is focused near positions 1, 2 and 3, respectively. These results indicate that the strongest surface plasmon energy (4.23 eV) and field intensity are generated when the nanohole is irradiated. Such strong surface plasmons have been observed in Pt nanostructures at similar energy levels due to an interband transition of the particles52,53,54. The diffraction pattern is also shown for position 3 on periodic Pt/nanoporous TiO2. To confirm the surface plasmons, we measured the reflectance of Pt/nanoporous TiO2 structures using an UV-VIS spectrometer. As shown in Fig. 5b, marks 1–3 are the calculated emission spectra of Pt/nanoporous TiO2 in water, while mark 4 is the measured reflectance of Pt/nanoporous TiO2 in air. The reflection peaks (colour dots) of mark 4 were found at the similar positions with respect to the simulated emission peaks shown at marks 1–3. The strongest reflection peak (purple arrow) of Pt/nanoporous TiO2 is shown at 245 nm (5.06 eV) by plasmon resonant coupling in air/Pt nanoholes. To understand the surface plasmon phenomena between two materials, we have to solve Maxwell's equation for the electromagnetic wave at the interface between two materials, which has relative dielectric functions ε1 ( = ε′1 + iε″1 = (n12 − κ12) + i(2n1κ1)) and ε2 ( = ε′2 + iε″2 = (n22 − κ22) + i(2n2κ2)) with the appropriated continuity relationship. Real and imaginary parts of the dielectric function are presented. The nj and κj are refractive index and extinction coefficient, respectively and j is 1 or 2. By boundary conditions, the dispersion relation for a wave propagating on the surface is  , where k ( = k′ + ik″), ω and c are the wave number and the frequency of the wave, the speed of light, respectively55. For k′ not to be purely imaginary, ε′1 = (n12 − κ12) < 0 and |ε′1| > ε′2 = (n22 − κ22). Based on this relationship, we have plotted a graph shown in Fig. S7. Since the surface plasmon energy occurs around |ε′1| ≈ ε′2, the surface plasmon wavelengths can be found from crossing points on the Pt line (black line). Compared to the water/Pt (green/black) interface, the air/Pt (blue/black) interface shows the surface plasmon phenomena at a slightly shorter wavelength. These wavelengths at the crossing points (red and green dots) of water/Pt and air/Pt in Fig. S7 are very close to the wavelengths at the strongest reflection peaks (red and green dots) as marked 1 and 4 in Figure 5b. Furthermore, the surface plasmon energy at the Pt/TiO2 interface is consistent with a dip (blue dot) near 450 nm. Therefore, matched data from the emission peak shown at mark 4 in Fig. 5b and the green dot shown in Fig. S7 indicate evidence of plasmon resonant coupling in air/Pt nanoholes under e-beam irradiation. There are only very small amounts of variation among the two layer calculation data (Fig. S7), the multi layer simulation results (Fig. 5b-1 ~ 3) and the experimental data (Fig. 5b-4). In addition, as shown in the electron profiles in Figs. 5c–h, the highest electric field intensities can trace electron irradiation paths (electric dipoles) and simultaneously, the electric field intensities in the Pt/nanoporous TiO2 structures are also strengthened near the electron irradiation paths by surface plasmons generated at the Pt nanoholes.
, where k ( = k′ + ik″), ω and c are the wave number and the frequency of the wave, the speed of light, respectively55. For k′ not to be purely imaginary, ε′1 = (n12 − κ12) < 0 and |ε′1| > ε′2 = (n22 − κ22). Based on this relationship, we have plotted a graph shown in Fig. S7. Since the surface plasmon energy occurs around |ε′1| ≈ ε′2, the surface plasmon wavelengths can be found from crossing points on the Pt line (black line). Compared to the water/Pt (green/black) interface, the air/Pt (blue/black) interface shows the surface plasmon phenomena at a slightly shorter wavelength. These wavelengths at the crossing points (red and green dots) of water/Pt and air/Pt in Fig. S7 are very close to the wavelengths at the strongest reflection peaks (red and green dots) as marked 1 and 4 in Figure 5b. Furthermore, the surface plasmon energy at the Pt/TiO2 interface is consistent with a dip (blue dot) near 450 nm. Therefore, matched data from the emission peak shown at mark 4 in Fig. 5b and the green dot shown in Fig. S7 indicate evidence of plasmon resonant coupling in air/Pt nanoholes under e-beam irradiation. There are only very small amounts of variation among the two layer calculation data (Fig. S7), the multi layer simulation results (Fig. 5b-1 ~ 3) and the experimental data (Fig. 5b-4). In addition, as shown in the electron profiles in Figs. 5c–h, the highest electric field intensities can trace electron irradiation paths (electric dipoles) and simultaneously, the electric field intensities in the Pt/nanoporous TiO2 structures are also strengthened near the electron irradiation paths by surface plasmons generated at the Pt nanoholes.
Discussion
Electrons and holes that migrate to the surface of metal electrodes can reduce and oxidize the reactants adsorbed on the metal surfaces, respectively. The reduction (Red) and oxidation (Ox) reactions can produce the reduction current and oxidation current as shown in the J-V measurement data in Fig. 3c. The oxidation current density (lower red curve) is less than reduction current (upper red curve) at 0 V under irradiation, meaning that the reaction Red ⇒ Ox + ne− is dominant on Pt/nanoporous TiO2 and available electrons are provided continuously, whereas the current density data (upper and lower black lines) of unirradiated devices seem not much different. When the strongly localised electric field oscillates across the Pt surface, as illustrated in Figs. 5c–h, the displacement of the electron density in the Pt surface by the electric field oscillation generates a Coulombic attraction force that can interact with environmental molecular ions, meaning that the eaq− and ·OH ions surrounded by water molecules can escape and attach to the Pt surface via localised surface plasmons. However, when the localised surface plasmon energy is less than the energy barrier of eaq− and ·OH, they cannot coherently oscillate or escape from their meta-stable state. With respect to the vacuum level, the work functions of eaq− and ·OH were calculated to be 1.6 eV and 7.2 eV, respectively, at pH 0. From the FDTD simulations, we obtained surface plasmon energy of 4.23 eV, which is 1.42 eV from the vacuum level and is higher than the energy level of eaq−, enabling electrons to escape from their meta-stable state and the escaped electrons to generate surface plasmons on the metal surface56,57. In addition, the presence of excited electrons indicates that excited holes with the same amount of energy (10.64 eV with respect to the vacuum level) exist. These excited holes can interact with ·OH on the surface of Pt. The same phenomenon is responsible for Förster resonant energy transfer (FRET), in which an excited donor transfers energy to an acceptor group through a non-radiative process58. In fact, the Schottky junction of Pt/TiO2 creates a space-charge region in the n-type TiO2 layer because the electrons diffuse from the TiO2 side to the Pt side whereas the holes move in the reverse direction. In the equilibrium state, an equal amount of electrons in Pt is trapped at the Pt/TiO2 interface and builds up an internal electric field (0.45 eV) from the TiO2 side toward the Pt side, preventing further movement of carriers. When surface plasmons are generated on Pt surface by beta radiation, electrons in Pt are pushed towards TiO2 by the electric field created from surface plasmons, which is higher than the internal electric field and holes move simultaneously towards the Pt/water surface interface. Accumulated holes can attract donors like negatively charged ions or radicals. Thus, the strong electric field enhancement can significantly increase the number of accumulated holes at the Pt/water interface and create a large internal potential difference. With the energy higher than the potential barrier (0.2 ~ 0.5 eV) of surrounding water molecules, solvated electrons (eaq−) can be attracted toward the Pt surface rapidly in water. Moreover, surface plasmons have a resonance frequency of a few hundred of GHz in visible wavelength. This means that strong Coulombic attraction force oscillates very fast to attract eaq− in water. When the distance between the TiO2 and Pt counter electrode is 5 cm, the electric field is approximately 0.09 V/cm and the speed of electrons in water reaches 1.6256 × 10−4 cm/s. If eaq− in water is 1 mm away from TiO2, it can move to the TiO2 surface in 603 s and most solvated electrons will not arrive quickly at the TiO2 electrode. Thus, as shown in Fig. S2, a slowly saturated curve of open circuit voltage is observed on TiO2 electrode under beta radiation, while the Pt/TiO2 electrode has a very fast saturated curve. The electric field of the TiO2 electrode is much weaker than that of the Pt/TiO2 electrode producing the surface plasmon effect and the difference in electric field intensity may affect the collection of eaq− in water. Once eaq− is arrived at the electrode surface, eaq− is injected without any energy loss because the electrochemical energy is higher than the conduction band edge (−0.1 ~ −0.2 VNHE) of TiO2.
In principle, photovoltaic devices, such as dye-sensitised solar cells and photochemical cells, use the similar mechanism, but sunlight produces very few free radicals because it is composed of photon energies that lie primarily in the visible range (380 nm–780 nm). Differently, beta radiation can produce many free radicals through the loss of kinetic energy in water. Then, the generation of localised surface plasmons on the Pt surface by beta radiation can enhance the chemical reactions involving free radicals produced by beta radiation in water. The reflection peak of Pt/nanoporous TiO2 at 5.04 eV and the similarity between the simulated emission spectra and measured reflection spectrum show that the surface plasmon resonance occurs at higher energy than the band gap energy of TiO2, indicating resonant energy transfer between TiO2 and surface plasmons59,60,61. Because the increased population of hot electrons generated by surface plasmons decreases the thickness of the Pt/TiO2 junction and increases its junction electric field62,63, the narrow junction enables carriers obtained from free radicals to efficiently move toward the contact metals without carrier relaxation in the thin film. We confirmed that significantly more power from the device with the plasmonic Pt layer was produced than that from the device without the plasmonic Pt layer. As shown in Fig. S12, increased surface plasmon energy can effectively transport hot carriers generated on a Pt surface. Therefore, we can conclude that the high power density obtained from our radiolytic cell may be attributed to the conversion of continuously generated free radicals with large electrochemical energy into electricity by the surface plasmon energy generated at the Pt surface. This finding reveals new mechanisms for power generation in radiolytic chemical cells. Our unique approach further paves the way for producing chemical cells with higher power density.
Methods
Sample preparation
A 2-μm-thick titanium film was deposited on a glass substrate using an RF sputtering system and an area of 1 cm2 was patterned for an electrode. The substrate was cleaned with a standard solvent cleaning process, dried under a flow of N2 gas and immediately anodised in a 0.01 wt% HF aqueous solution under an applied voltage of 40 V for 5 min. Immediately after cleaning and drying the anodised Ti films, the substrate was annealed in a convection oven at 450°C for 2 hours. A 50-nm-thick Pt film was deposited on the thermally oxidised Ti films using an RF sputtering system. A copper wire was connected to the electrode of each sample and covered with epoxy to electrically isolate the electrolyte.
Structural and optical properties
Scanning electron microscopy (SEM) was performed using an FEI Quanta 600 FEG extended vacuum scanning electron microscope with an accelerating voltage of 10 kV and an energy dispersive spectrometer (Noran System Six). X-ray diffraction (XRD) analysis was conducted using a Rigaku Miniflex 600 X-ray diffractometer with Cu Kα radiation. The reflection spectrum was measured using a Perkin-Elmer lambda 25 UV-VIS spectrometer and variable-angle reflectance accessory.
Electrical properties
Consecutive J-V measurements were collected from 1.0 V to −1.5 V with respect to Ag/AgCl reference electrodes in a three-electrode system at a fixed scan rate of 0.05 V/s. The electrolyte solution was 1 M KOH (Sigma Aldrich, 99%). A radioisotope source (Sr-90/Y-90, 15 mCi) sealed in stainless steel was chosen for our experiment. The distance between the electrode and the radiation source required to maintain a constant activity of 15 mCi at the surface of the device was determined to be approximately 1 mm. A potentiostat (DY2322, Digi-Ivy) was connected to the three (reference, counter and working) electrodes for data collection. All experiments were performed in a dark room to eliminate the effects of a photocurrent. In addition, to ensure that the reaction only involved diffused radicals, the solution was not agitated.
FDTD simulation
We used Pt (50 nm)/nanoporous TiO2 (1 μm) composed of a periodic array of nanoholes with a diameter of 10 nm and a depth of 505 nm. The electron beam was modelled as a series of closely spaced dipoles with a temporal phase delay defined by the velocity of the electron beam. In the absence of a structure, an electron beam moving at a constant velocity does not generate any radiation. The material properties used in the calculation are based on the dispersion data given in refs. 64 and 65. The detailed electron irradiation profiles at the different positions at the bottom level of the nanoholes in the supplementary information show the strong influence of the Pt/nanoporous TiO2 structures on the scattering direction.
References
Love, C. J. Handbook of Cardiac Pacing. (Landes Bioscience, Austin, 1999).
Singh, N. Radioisotopes-Applications in physical sciences. (InTech inc, Rijeka, 2011).
Corliss, W. R. & Harvey, D. G. Radioisotopic power generation. (Prentice-Hall, Englewood Cliffs, 1964).
Bower, K. E., Barbanel', Y. A., Shreter, Y. G. & Bohnert, G. W. Polymers, Phosphors and Voltaics for Radioisotope Microbatteries. (CRC Press, Boca Raton, 2002).
Pfann, W. G. & Van Roosbroeck, W. Radioactive and photoelectric p-n junction power sources. J. Appl. Phys. 25, 1422 (1954).
Rappaport, P. The electron-voltaic effect in pn junctions induced by beta particle bombardment. Phys. Rev. 93, 246–247 (1954).
Olsen, L. C., Cabauy, P. & Elkind, B. J. Betavoltaic power sources. Phys. Today 65, 35–38 (2012).
Ko, W. & Hynecek, J. Implant evaluation of a nuclear power source-Betacel® battery. IEEE trans. on Biomed. Engr. 238–241 (1974).
Huffman, F. & Norman, J. Nuclear-fueled cardiac pacemakers. Chest 65, 667–672 (1974).
Wei, L. Parametric studies and optimization of the beta-voltaic cell--II open-circuit voltage and power efficiencies. Solid-State Elec. 18, 71–77 (1975).
Liu, B., Chen, K. P., Kherani, N. P. & Zukotynski, S. Power-scaling performance of a three-dimensional tritium betavoltaic diode. Appl. Phys. Lett. 95, 233112 (2009).
Eiting, C. J. et al. Demonstration of a radiation resistant, high efficiency SiC betavoltaic. Appl. Phys. Lett. 88, 064101 (2006).
Lu, M., Wang, G. & Yao, C. Gallium nitride for nuclear batteries. Adv. Mater. Res. 343–344, 56–61 (2012).
Sun, W. et al. A Three-Dimensional Porous Silicon p-n Diode for Betavoltaics and Photovoltaics. Adv. Mater. 17, 1230–1233 (2005).
Duggirala, R., Lal, A. & Radhakrishnan, S. Radioisotope thin-film powered microsystems. (Springer, New York, 2010).
Wacharasindhu, T., Kwon, J. W., Meier, D. E. & Robertson, J. D. Radioisotope microbattery based on liquid semiconductor. Appl. Phys. Lett. 95, 014103 (2009).
Murray, R. Nuclear energy (Pergamon Press, Oxford, 1980).
Collinson, E., Dainton, F. S. & Kroh, J. Effects of linear energy transfer of the radiolysis of water and heavy water. Nature 187, 475–477 (1960).
Khan, K. A. The radiation chemistry of water. J. Chem. Soc. Pak 3, 105–110 (1981).
Jonah, C. D. A short history of the radiation chemistry of water. Rad. Res. 144, 141–147 (1995).
Seino, S. et al. Enhancement of hydrogen evolution yield from water dispersing nanoparticles irradiated with gamma-ray. J. Nucl. Sci. Technol. 38, 633–636 (2001).
Cecal et al. Use of some oxides in radiolytical decomposition of water. Rad. Phys. Chem. 62, 333–336 (2001).
Seino, S. et al. Hydrogen evolution from water dispersing nanoparticles irradiated with gamma-ray/size effect and dose rate effect. Scripta Mater. 44, 1709–1712 (2001).
Ershov, B. G. & Gordeev, A. V. A model for radiolysis of water and aqueous solution of H2, H2O and O2 . Rad. Phys. Chem. 77, 928–935 (2008).
Laverne, J. A. & Tandon, L. H2 production in the radiolysis of water on UO2 and other oxides. J. Phys. Chem. B 107, 13623–13623 (2003).
Wada, Y., Kawaguchi, K. & Myouchin, M. Decomposition of water and production of H2 using semiconductor-photocatalytic effect induced by gamma ray from high radioactive waste. Progress in Nuclear Energy 29, 251–256 (1995).
Laverne, J. A. & Tonnies, S. E. H2 production in the radiolysis of aqueous SiO2 suspensions and slurries. J. Phys. Chem. B 107, 7277–7280 (2003).
Schierbaum, K. D. et al. The interaction of Pt with TiO2(110) surfaces: a comparative XPS, UPS, ISS and ESD study. Surf. Sci. 345, 261–173 (1996).
Borodin, A. & Reichling, M. Characterizing TiO2(110) surface states by their work function. Phys. Chem. Chem. Phys. 12, 15442–15447 (2011).
Lide, D. R. CRC Handbook of chemistry and physics (CRC Press, Boca Raton, 2005).
Heimann, D. Radiative decay of surface palsmons excited by fast electrons on periodically modulated silver surfaces. J. Phys. C 10, 397–405 (1977).
Bashevoy, M. V., Jonsson, F., Krasavin, A. V. & Zheludev, N. I. Generation of traveling surface plasmon waves by free-electron impact. Nano Lett. 6, 1113–1115 (2006).
Cai, W. et al. Efficient generation of propagating plasmons by electron beams. Nano Lett. 9, 1176–1181 (2009).
Koh, A. L. et al. High-resolution mapping of electron-beam-excited plasmon modes in lithographically defined gold nanostructures. Nano Lett. 11, 1323–1330 (2011).
Das, P., Chini, T. K. & Pond, J. Probing higher order surface plasmon modes on individual truncated tetrahedral gold nanoparticle using cathodoluminescence imaging and spectroscopy combined with FDTD simulations. J. Phys. Chem. C 116, 15610–15619 (2012).
Petrik, N. G. & Kimmel, G. A. Electron-stimulated reactions in thin D2O films on Pt(111) mediated by electron trapping. J. Chem. Phys. 8, 3727–3735 (2004).
Koitaya, T., Nakamura, H. & Yamashita, K. First-principle calculations of solvated electrons at protic solvent-TiO2 interfaces with oxygen vacancies. J. Phys. Chem. 113, 7236–7245 (2009).
Young, R. M. & Neumark, D. M. Dynamics of solvated electrons in clusters. Chem. Rev. 112, 5553–5577 (2012).
Buck, E. C. Effects of electron irradiation of rutile. Radiat. Eff. Defect Solids 133, 141–152 (1995).
Grimes, C. A. & Mor, G. K. TiO2 nanotube arrays: synthesis, properties and applications. (Springer, New York, 2009).
Drouin, D. et al. CASINO V2.42: a fast and easy-to-use modeling tool for scanning electron microscopy and microanalysis users. Scanning 29, 92–101 (2007).
Lewis, E. E. Fundamentals of nuclear reactor physics. (Academic Press, London, 2008).
Caër, S. L. Water radiolysis: influence of oxide surfaces on H2 production under ionizing radiation. Water 3, 235–253 (2011).
Klein, C. A. Bandgap dependence and related features of radiation ionization energies in semiconductors. J. Appl. Phys. 39, 2029–2038 (1968).
Boag, J. W. & Hart, E. J. Absorption spectra in irradiated water and some solutions: absorption spectra of ‘hydrated’ electron. Nature 197, 45–47 (1963).
Keene, J. P. Absorption spectra in irradiated water and some solutions: optical absorptions in irradiated water. Nature 197, 47–49 (1963).
Avel, B. Hydrated interfacial ions and electrons. Annu. Rev. Phys. Chem. 64, 533–552 (2013).
Zhu, D., Zhang, L., Ruther, R. E. & Hamers, R. J. Photo-illuminated diamond as a solid-state source of solvated electrons in water for nitrogen reduction. Nature Mater. 12, 836–841 (2013).
Hase, H. & Higashimura, T. Trapped and solvated electrons produced in ethanol glass in the presence of an applied electric field. J. Phys. Chem. 83, 822–823 (1979).
Schmidt, K. H. & Buck, W. L. Mobility of the hydrated electron. Science 151, 70–71 (1966).
Henglein, A., Ershov, B. G. & Malow, M. Absorption spectrum and some chemical reactions of colloidal platinum in aqueous solution. J. Phys. Chem. 99, 14129–14136 (1995).
Rivadulla, J. F. et al. Optical properties of platinum particles synthesized in microemulsions. J. Phys. Chem. B 101, 8997–9004 (1997).
Bassett, P. J. et al. Helium-I photoelectron spectra of tetrakis(trifluorophosphine)-nickel(0), -palladium(0) and -platinum(0). J. Chem. Soc., Dalton Trans. 21, 2316–2319 (1974).
Maier, S. A. Plasmonics: Fundamentals and applications. (Springer, New York, 2007).
Atwater, H. A. & Polman, A. Plasmonics for improved photovoltaic devices. Nature Materials 9, 205–213 (2010).
Stratakis, E. & Kymakis, E. Nanoparticle-based plasmonic organic photovoltaic devices. Materials Today 16, 133–146 (2013).
Fadhali, M. Advanced Photonic Sciences. (Intech, Rijeka, 2012).
Murakoshi, K. & Uosaki, K. Photon emission at metal/solution interface induced by electron injection form solvated electrons. J. Vac. Sci. Technol. A 10, 2981–2984 (1992).
Murakoshi, K. & Uosaki, K. Observation and mechanism of photon emission at metal-solution interfaces. Phy. Rev. B 47, 2278–2288 (1993).
Warren, S. C. & Thimsen, E. Plasmonic solar water splitting. Energy Environ. Sci. 5, 5133–5146 (2012).
Kempa, K. et al. Hot electron effect in nanoscopically thin photovoltaic junctions. Appl. Phys. Lett. 95, 233121 (2009).
Wang, F. & Melosh, N. A. Power-independent wavelength determination by hot carrier collection in metal-insulator-metal devices. Nature Communications 4, 1711 (2013).
Devore, J. R. Refractive indices of rutile and sphalerite. J. Opt. Soc. Am. 41, 416–419 (1951).
Palik, E. D. Handbook of optical constants of solids. (Academic Press, London, 1997).
Acknowledgements
The authors are grateful for useful discussions for XPS analysis with Mr. Brian Porter and for TEM sample preparation with Ms. Jessica R. Terbush in the Material Research Center at the Missouri University of Science and Technology. The authors are also thankful for optical measurements and detailed discussions with Dr. Ping Yu at the University of Missouri.
Author information
Authors and Affiliations
Contributions
B.H.K. and J.W.K. performed the experiments, analysed the data, discussed the results and commented on the manuscript. J.W.K. conceived and supervised this study and provided intellectual and technical guidance.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
supplementary information
Supplementary Information
Movie S1a
Supplementary Information
Movie S1b
Supplementary Information
Movie S2a
Supplementary Information
Movie S2b
Supplementary Information
Movie S3a
Supplementary Information
Movie S3b
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Kim, B., Kwon, J. Plasmon-assisted radiolytic energy conversion in aqueous solutions. Sci Rep 4, 5249 (2014). https://doi.org/10.1038/srep05249
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05249
This article is cited by
-
Exploratory study of betavoltaic battery using ZnO as the energy converting material
Nuclear Science and Techniques (2019)
-
Impact of Substrate Types on Structure and Emission of ZnO Nanocrystalline Films
Journal of Electronic Materials (2018)
-
Evaluation of a Silicon 90Sr Betavoltaic Power Source
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.