Abstract
Glass is a freezing phase of a deeply supercooled liquid. Despite its simple definition, the origin of glass forming ability (GFA) is still ambiguous, even for binary Cu-Zr alloys. Here, we directly study the stability of the supercooled Cu-Zr liquids where we find that Cu64Zr36 at a supercooled temperature shows deeper undercoolability and longer persistence than other neighbouring compositions with an equivalent driving Gibbs free energy. This observation implies that the GFA of the Cu-Zr alloys is significantly affected by crystal-liquid interfacial free energy. In particular, the crystal-liquid interfacial free energy of Cu64Zr36 in our measurement was higher than that of other neighbouring liquids and, coincidently a molecular dynamics simulation reveals a larger glass-glass interfacial energy value at this composition, which reflects more distinct configuration difference between liquid and crystal phase. The present results demonstrate that the higher crystal-liquid interfacial free energy is a prerequisite of good GFA of the Cu-Zr alloys.
Similar content being viewed by others
Introduction
Understanding glass-forming ability (GFA)1,2,3 of metallic glasses (MGs) is a long-standing fundamental issue for basic science and their applications. With progress in strategies for alloying design, over 30 mm in diameter bulk metallic glasses (BMGs) prepared by directly copper mold cast technique were achieved in four alloy systems, i.e., 73 mm ZrCuAgAlBe4, 50 mm TiZrNiCuBe5, 40 mm PdNiCuP6, 35 mm LaCuAgAlCoNi7. However, the exact origin for the GFA in BMGs has not yet been completely understood8,9,10,11,12,13,14,15,16,17. Rather than the complexity in multi-component BMGs, binary Cu-Zr BMGs11 (its critical diameter is larger than 1 mm) have been intensively studied to figure out the GFA, because of its simplicity and showing very sensitive dependence of composition on the critical size forming glassy phase, even narrow down to 1 at. %.
Though enormous studies11,12,13,14,15,16,17, clear explanations have not been suggested for the origin of the good GFA for the Cu-Zr BMGs. For instance, in thermodynamic point of view, Kwon et al.16 reported that the good GFA of Cu64Zr36 was attributed to the relatively small difference of Gibbs free energy between amorphous and crystal phases. Wang et al.11 pointed out that the GFA of Cu-Zr MGs was significantly influenced by the crystallization of competing phases. In addition, it was reported that the liquid structure of the Cu-Zr MGs could affect their thermal stability and the GFA; Yang et al.15 addressed that a relatively high atomic-packing efficiency of short range order (SRO) on the Cu64Zr36 BMG was attributed to the good GFA. On the other hand, in the kinetic point of view, Li et al.12 demonstrated that the composition forming the BMGs on Cu-Zr alloys had higher density than other Cu-Zr compositions. This suggests denser metallic glasses have higher viscosity in the supercooled state, resulting in the good GFA. Moreover, Bendert et al.17 suggested that the GFA of Cu-Zr alloys resulted from the different fragility at the supercooled liquid state and also near glass-transition temperature (Tg), based on the measurement of thermal expansion coefficients. In other words, the stronger viscous behaviour of Cu-Zr liquid gives the better GFA. Nevertheless, the direct observation of such strong viscosity behaviour of the supercooled liquids forming Cu-Zr BMGs has not been reported yet. Therefore, the GFA is still ambiguous even for binary Cu-Zr MGs, although significant recent efforts have been devoted to study the GFA.
One of determinant factors to facilitate the good GFA that has not been considered in detail is the stability of supercooled Cu-Zr liquids. Since glasses are a freezing phase of deeply supercooled liquid, the better stability should give the deeper undercooling, resulting in the vitrification of the supercooled liquid. Therefore, we should directly study the stability of the supercooled Cu-Zr liquids. We report crystal-liquid interfacial free energy and glass-glass interfacial energy of Cu-Zr alloys, resulting in the stability of the supercooled Cu-Zr liquids using a containerless technique, i.e., electrostatic levitation (ESL), providing the deep supercooling and using molecular dynamics (MD) simulation study. It is found that for a given composition the higher GFA, the higher undercoolability and the longer persistence of a supercooled liquid state. We provide compelling evidence to demonstrate that the interfacial free energy is a decisive factor to stabilize the supercooled liquid and thus affect the GFA, which is a novel approach to understand the GFA of the Cu-Zr alloys.
Results
Undercoolability and persistence of supercooled liquid
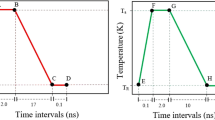
Figure 1a shows a representative heating and cooling curve of a Cu-Zr sample. The sample is heated over their liquidus temperature (Tl) and cools down radiatively by turning off the heating lasers. Undercoolability is one of the signatures for the liquid stability, described by the degree of supercooling of the liquids, i.e., ΔT/Tl = (Tl − Tr)/Tl, where Tl and Tr are the liquidus and recalescence temperatures, respectively. Figure 1b shows the reduced undercooling values (ΔT/Tl) of various Cu100-xZrx (x = 35–54.3 at. %) alloy liquids. Interestingly, maxima are observed at Cu64Zr36 (ΔT/Tl = 0.24 ± 0.01), Cu56Zr44 (ΔT/Tl = 0.30 ± 0.01) and Cu50Zr50 (ΔT/Tl = 0.32 ± 0.01), regardless different liquidus temperatures. The maxima in undercooling are consistent with the critical thickness or the GFA on Cu-Zr MGs12 and thermal expansion coefficient maxima in Cu-Zr liquids17. The maxima in undercooling mean that the supercooled liquids of Cu64Zr36, Cu56Zr44 and Cu50Zr50 have better stability, compared with neighbouring compositions. Based on the classical nucleation theory (CNT)18, the deeper undercooling reflects the higher nucleation barrier. Therefore, the liquids showing undercooling maxima (i.e., better stability) should be expected to show longer persistence at a same degree of the supercooled temperature than the neighbouring composition liquids.
Time-Temperature curve of Cu64Zr36 and undercoolability of Cu100-xZrx (x = 35–54.3 at.%) alloys.
(a) A typical Time-Temperature curve of the Cu64Zr36 binary alloy by the electrostatic levitation (ESL) experiment, where Ts is the solidus temperature, Tl is the liquidus temperature and Tr is the recalescence temperature. (b) Undercoolability, ΔT/Tl = (Tl − Tr)/Tl, of Cu100-xZrx (x = 35–54.3 at. %) as a function of the Zr concentration. Three different liquidus temperatures of Cu-Zr alloys are used to determine the undercoolability, i.e., Tl from present ESL experiments ( ) and from ref. 30 (
) and from ref. 30 ( ) and ref. 31 (
) and ref. 31 ( ) phase diagrams. Meshed column is the result of the average liquidus temperature from the three liquidus Tl.
) phase diagrams. Meshed column is the result of the average liquidus temperature from the three liquidus Tl.
To verify the stability of the supercooled liquid as a function of time, we carried out Time-Temperature-Transformation (TTT) experiments. In particular, we focus on the Cu64Zr36, since the origin of the higher GFA for the most studied composition is still unclear. Figure 2 shows the TTT-diagram of Cu100-xZrx (x = 35–38.2 at. %) liquids. At the same reduced supercooling temperature, T/Tl = 0.865, as an example, Cu64Zr36 liquid indeed persists for much longer time 455 s in the supercooled liquid state than other neighbouring compositions, 124 s and 16 s for Cu63.1Zr36.9 and Cu61.8Zr38.2, respectively. This experimental observation is consistent with the calculated TTT-diagram of Cu64Zr36 (red) and Cu61.8Zr38.2 (blue) from ref. 19, although the exact values are different. According to the CNT, the nucleation barrier (ΔG*) resisting the crystallization is determined by two factors, crystal-liquid interfacial free energy (σ) and Gibbs free energy difference of liquid and crystal (ΔGv), i.e., ΔG* = 16πσ3/3(ΔGv)218. Here, the same reduced temperature is assumed to give the same driving force for the nucleation (in case of Turnbull's approximation, ΔGv = ΔHf(1 − T/Tl), where ΔHf is the fusion enthalpy). This assumption is reasonable because ΔHf should not be significantly different for the Cu-Zr liquids within such a small composition range (35–38.2 at. % of Zr). Accordingly, the longer persistence of the supercooled liquid at the same T/Tl indicates that the stability of the supercooled liquids is decisively determined by the interfacial free energy (σ).
Reduced Time-Temperature-Transformation (TTT) diagram of Cu100-xZrx (x = 35–38.2 at.%) alloys.
Tl at reduced temperature (T/Tl) is the average value of the three different liquidus temperatures (Tl: present, Tl: ref. 30, Tl: ref. 31).The blue and red lines are of calculated TTT curves from ref.20 and dots are of experimental results in present study using the ESL technique. The inset is magnified from the dots with dashed guide lines for eyes.
Interfacial free energy
Since the deeper undercooling and the longer persistence of the supercooled liquid Cu64Zr36 imply higher interfacial free energy, to confirm it, we estimate the crystal-liquid interfacial free energy from the undercooling data using the CNT. To initiate crystallization reaction, at least one critical nucleus should be formed in the supercooled liquid. This requires that the number of the critical nucleus in the supercooled liquid should be greater than one with a given liquid volume V, a steady state nucleation rate Is and time t at a certain temperature T18, i.e.,

Here, the steady state nucleation rate Is per unit volume at temperature T is given by

where η, λ, n*, δμ, kB, NA and ΔGn* are the viscosity, the average atomic jump distance, the number of atoms in the critical nucleus, the Gibbs free energy difference between the initial and final phases per atom, the Boltzmann's constant, the Avogadro number and the work (i.e., nucleation barrier) of critical cluster formation, respectively. The work ΔGn* is determined by the Gibbs free energy difference ΔGv = δμ/v, the interfacial free energy (σ) and the average atomic volume (v). As expected, it is found that the Cu64Zr36 alloy, having the higher GFA12, exhibits the highest crystal-liquid interfacial free energy value in Figure 3, which is consistent with the undercoolability and TTT-diagram results in Figures 1b and 2. It should be mentioned that the density and viscosity of Cu-Zr liquids measured in this study show weak composition dependence, which is reasonable with the narrow composition range. This is consistent with a previous report17 that show no volume anomaly of Cu-Zr alloy liquids with compositions. Thus no composition effect of density and viscosity within the temperature range was found to estimate the interfacial free energy of Cu-Zr alloys.
Interfacial free energies of Cu100-xZrx (x = 35–38.2 at.%) alloys.
(a) Estimated crystal-liquid interfacial free energies (σ) from the undercooling data in the ESL experiment using the classical nucleation theory (CNT) and Turnbull's coefficients (α) of Cu100-xZrx (x = 35–38.2 at. %) alloys. (b) Calculated glass-glass interfacial energy of Cu-Zr metallic glasses (MGs) at 800 K as a function of Zr composition together with the critical thickness for the glass formation in the Cu-Zr alloy system reported in ref. 12.
In addition, the glass-glass interfacial energies for Cu100-xZrx (x = 30–52 at. %) MGs were calculated at 800 K by molecular dynamics (MD) simulations in Figure 3b. It should be stressed that a prerequisite for calculating crystal-liquid interfacial free energies is the crystal structure and the orientation of the crystal at the interface. Unfortunately, such information is not available as we change the composition of the alloys. And thus instead of directly calculating crystal-liquid interfacial free energies, we calculated the glass-glass interfacial energies of Cu-Zr MGs (see the details in Supporting Online Material). Since the difference of regularity or atomic packing density of short range order in bulk and surface of the glass is dependent of compositions, the interfacial energy between the glasses would show the dependence of composition. This gives the relation of short range order and GFA with composition. Although these data are not exactly the same as those for the crystal-liquid interfacial free energies, they still interestingly provide the same trends as the interfacial free energies of crystal-supercooled liquid of Cu100-xZrx (x = 35–38.2 at. %) estimated from the undercooling data.
Configurational differences causing interfacial free energy
Following the Turnbull's explanation of the stability of the supercooled liquid (or the high nucleation barrier) by crystal-liquid interface structure20, the higher interfacial free energy for Cu64Zr36 alloy implies the larger difference of the configurational ordering between the supercooled liquid and the crystal. Unlike crystal-gas interface, atoms in the liquid near a crystal show ordering, called neg-entropic ordering. When the atomic configurational ordering at the interface is more different from that of the crystal, the larger interfacial free energy forms and thus leads to the high nucleation barrier21,22 as follows.

where Ni is the number of atoms in the interface, N is the number of atoms in the crystal plane, ΔSconfig(bulk) is the configurational entropy of the bulk crystal, ΔSconfig(interface) is the configurational entropy of the interface and ΔSf is the fusion entropy per atom. The higher Turnbull's coefficient (α) on Cu64Zr36 (αT = 0.519), as shown in Figure 3a, indicates that the configurational ordering between the crystal and the supercooled liquid of Cu64Zr36 differs from that of neighbouring compositions.
To further confirm the higher interfacial free energy for Cu64Zr36 alloy, we further carried out synchrotron X-ray diffraction measurements for Cu100-xZrx (x = 35–38.2 at. %) MGs at ambient temperature. It is indeed found that the Cu64Zr36 MG had the highest dense-packing of icosahedral short range ordering (ISRO) than other compositions, which is consistent with the recently reported results for Cu-Zr MGs15. Similar to other studies23, a high fraction of icosahedral-like clusters in Cu64Zr36 MG was also detected after Voronoi tessellation analyses of the results obtained by reverse Monte Carlo (RMC) simulation to the experimental data15. Since the icosahedral short range order (ISRO) clearly differs from the short range orders in Cu-Zr crystal phases, the highest atomic packing on Cu64Zr36 MG could result in the large difference of configurational entropy between crystal and amorphous alloy. It is worth to note an opposite example which validates the conclusion; a liquid forming Ti-Zr-Ni icosahedral quasicrystal phase (i-phase) showed a lower interfacial free energy (σ = 0.06 J/m2) and αT = 0.32 with small undercooling (ΔT/Tl = 0.1), since the both local orders of the liquid and i-phase are same local ordering, i.e, icosahedral order24,25.
The highest interfacial free energy on the Cu64Zr36 liquid and glass links with the higher atomic-packing efficiency on Cu64Zr36 BMG15, i.e., more difference of configurational ordering between the liquid and the crystal. Hence, the good GFA on Cu64Zr36 comparing with neighbouring compositions is attributed to the stability of supercooled liquid with the high interfacial free energy. Moreover, a recent simulation study26 revealed the importance of crystal-liquid interface structure for the GFA; the poorer crystal-liquid interfacial structure, the larger difference of local ordering between liquid and crystal, leading to the better GFA for Cu50Zr50 as compared with Ni50Al5026, which is consistent with this study.
Discussion
We carried out molecular dynamics (MD) simulation to calculate glass-glass interfacial energies for Cu100-xZrx (x = 30–52 at. %) MGs at 800 K (Fig.3b). Interestingly, the glass-glass interfacial energies at 800 K provide the same trends with the crystal-supercooled liquid interfacial free energy of Cu100-xZrx (x = 35–38.2 at. %) estimated from undercooling data (Fig.3). Since the glass-glass interface is formed by welding two glasses, the interfacial energy reflects the different degree of randomness in short range order in bulk and interface of the glasses due to the more excessive volume on surface than in bulk of the glass. In other words, the surface has more defective short range ordering27. Therefore, when the glass has the better regularity or the higher packing density of the ISRO in bulk, the larger difference of the excessive volume between the bulk and the surface is given, which causes the higher interfacial energy. Accordingly, the higher interfacial energy of Cu64Zr36 compared with the neighbour compositions supports that the better regularity or higher packing density of ISRO results in the better GFA15. Moreover, other glass forming compositions, i.e., Cu56Zr44 and Cu50Zr50 also show higher glass-glass interfacial free energies.
One would expect that the glass-glass interfacial energy would eventually diminish at high temperatures. One might also expect that such temperature is sensitive to alloy compositions, i.e., a higher interfacial energy usually corresponds to a higher diminishing temperature because the reduction of the interfacial energy at the high temperature is closely related to the glass relaxation time and the higher interfacial energy may be related to a higher viscosity. However, further simulation needs to be carried out to confirm this hypothesis.
The C-curve in the TTT diagram is usually observed in bulk metallic glasses, due to the result of the competition of two characteristic times, i.e., τn and τD for nucleation and viscosity (or diffusion), respectively. Below a nose temperature in TTT diagram, τD for viscosity property governs the GFA. In contrast, τn for nucleation governs the GFA above the nose temperature. Although electrostatic levitation can easily achieve deeper supercooling state than other methods, the cooling rate by radiation on Cu-Zr alloys is not fast enough to bypass the nose temperature in TTT diagram. This prevents from verifying the reported characteristic viscosity behaviour (i.e., fragility)17 or the role of τD to explain the good GFA on Cu-Zr alloys. Instead, we can clearly see the characteristics of τn for nucleation with the higher undercoolability, the longer persistence of supercooled liquid state and the higher interfacial free energy (i.e., nucleation barrier), which reflects the stability of the supercooled Cu-Zr liquids in figures 1, 2 and 3. Therefore, if a moderate cooling rate is given, the stability of supercooled Cu-Zr liquids should be kept and the liquids can become glasses.
In conclusion, we investigate the origin of the GFA on a Cu-Zr alloy system. We found that Cu64Zr36 showed better undercoolability and stayed in supercooled liquid state for longer time, compared with neighbouring compositions. Under the same driving force, the longer persistence of the supercooled liquid on Cu64Zr36 revealed that interfacial free energy was the key factor for the stability of the supercooled liquid. The highest interfacial free energy on Cu64Zr36 estimated from both undercooling experiment and simulation supports this scenario, on comparing with the neighbouring compositions. Our findings could have an implication that the GFA for various compositions in a given alloy system is controlled by the interfacial free energy between crystal and supercooled alloy liquids. The higher interfacial free energy, the higher the GFA. This should certainly be validated in other MG systems.
Methods
Sample preparation
Spherical Cu100-xZrx (x = 35–54.3 at. %) alloys were prepared by an arc-melting with high-purity copper (Cu, 99.99%) and zirconium (Zr, 99.995%) slugs under high-purity argon (Ar, 99.9999%) atmosphere. To avoid reaction with oxygen, a piece of Zr was used as an oxygen getter. The samples were melted at least four times for the homogeneity of each composition.
Undercooling experiment and data acquisition
The levitated samples with 2–3 mm in diameter were melted under high vacuum condition in the range of 10−6–10−7 Torr by CO2 heating lasers with triangle arrangement for symmetrical heating. Detailed description of the electrostatic levitation (ESL) equipment is given in refs.28 and 29. The samples were heated over their liquidus temperature (Tl) and cooled radiatively by turning off the heating lasers. The sample temperature was measured for every 6 ms by two infrared pyrometers with InGaAs detector operating at 1.55 μm wavelength (547–1973 K) and 1.6 μm wavelength (773–2773 K). The spectral emissivity (Eλ) of Cu-Zr alloy is determined with the known solidus temperature (Ts) by the phase diagram of the binary Cu-Zr alloys30.
Synchrotron X-ray scattering experiment
For the structural study, the synchrotron X-ray scattering experiments were carried out in Hasylab in Germany15 and in PAL in Republic of Korea. Related thermophysical parameters and MD simulations details are given in Supporting Online Material.
References
Turnbull, D. Under what conditions can a glass be formed? Contemp. Phys. 10, 473–488 (1969).
Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Mater. 48, 279–306 (2000).
Lu, Z. P. & Liu, C. T. Glass formation criterion for various glass forming systems. Phys. Rev. Lett. 91, 115505 (2003).
Lou, H. B. et al. 73 mm-diameter bulk metallic glass rod by copper mould casting. Appl. Phys. Lett. 99, 051910 (2011).
Tang, M. Q. et al. TiZr-base bulk metallic glass with over 50 mm in diameter. J. Mater. Sci. Technol. 26, 481–486 (2010).
Nishiyama, N. & Inoue, A. Flux treated Pd-Cu-Ni-P having low critical cooling rate. Mater. Trans. JIM 38, 464–472 (1997).
Jiang, Q. K. et al. La-based bulk metallic glasses with critical diameter up to 30 mm. Acta Mater. 55, 4409–4418 (2007).
Finney, J. L. Modelling the structure of amorphous metals and alloys. Nature 266, 309–314 (1977).
Miracle, D. B. A structural model for metallic glasses. Nat. Mater. 3, 697–702 (2004).
Sheng, H. W., Luo, K. L., Alamgir, F. M., Bai, J. M. & Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 439, 419–425 (2006).
Wang, D. et al. Bulk metallic glass formation in the binary Cu-Zr system. Appl. Phys. Lett. 84, 4029–4031(2004).
Li, Y., Guo, Q., Kalb, J. A. & Thompson, C. V. Matching glass-forming ability with the density of the amorphous phase. Science 322, 1816–1819 (2008).
Cheng, Y. Q., Sheng, H. W. & Ma, E. Relationship between structure, dynamics and mechanical properties in metallic glass-forming alloys. Phys. Rev. B 78, 014207 (2008).
Jakse, N. & Pasturel, A. Glass forming ability and short-range order in a binary bulk metallic glass by ab initio molecular dynamics. Appl. Phys. Lett. 93, 113104 (2008).
Yang, L. et al. Atomic-scale mechanisms of the glass-forming ability in metallic glasses. Phys. Rev. Lett. 109, 105502 (2012).
Kwon, O. J., Kim, Y. C., Kim, K. B., Lee, Y. K. & Fleury, E. Formation of amorphous phase in the binary Cu-Zr alloy system. Met. Mater. Int. 12, 207–212 (2006).
Bendert, J. C., Gangopadhyay, A. K., Mauro, N. A. & Kelton, K. F. Volume expansion measurements in metallic liquids and their relation to fragility and glass forming ability: An energy landscape interpretation. Phys. Rev. Lett. 109, 185901 (2012).
Kelton, K. F. Solid State Physics (Academic Press, Boston, 1991).
Ge, L. et al. Prediction of the glass forming ability in Cu-Zr binary and Cu-Zr-Ti ternary alloys. Intermetallics 16, 27–33 (2008).
Turnbull, D. Formation of crystal nuclei in liquid metals. J. Appl. Phys. 21, 1022–1028 (1950).
Spaepen, F. & Meyer, R. B. The surface tension in a structural model for the solid-liquid interface. Scr. Metall. 10, 257–263 (1976).
Spaepen, F. A structural model for the solid-liquid interface in monatomic system. Acta Metall. 23, 729–743 (1975).
Cheng, Y. Q. & Ma, E. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci. 56, 379–473 (2011).
Kelton, K. F. et al. First X-ray scattering studies on electrostatically levitated metallic liquids: demonstrated influence of local icosahedral order on the nucleation barrier. Phys. Rev. Lett. 90, 195504 (2003).
Lee, G. W. et al. Link between liquid structure and the nucleation barrier for icosahedral quasicrystal, polytetrahedral and simple crystalline phases in Ti-Zr-Ni alloys: Verification of Frank's Hypothesis. Phys. Rev. B 72, 174107 (2005).
Tang, C. & Harrowell, P. Anomalously slow crystal growth of the glass-forming alloy CuZr. Nat. Mater. 12, 507–511 (2013).
Ritter, Y., Sopu, D., Gleiter, H. & Albe, K. Acta Mater. 59, 6588–6593 (2011).
Rhim, W. -K. et al. An electrostatic levitation for high-temperature containerless materials processing in -g. Rev. Sci. Instrum. 64, 2964–2970 (1993).
Lee, G. W., Jeon, S. & Kang, D.-H. Crystal-liquid interfacial free energy of supercooled liquid Fe using a containerless technique. Cryst. Growth Des. 13, 1786–1792 (2013).
Gale, W. F. & Totemeier, T. C. Smithels metals reference book (Butterworth-Heinemann, Oxford, 8th ed.2004).
Okamoto, H. Cu-Zr (Copper-Zirconium). J. Phase Equilib. Diffus. 29, 204 (2008).
Acknowledgements
Financial supports from the National Key Basic Research Program of China (2012CB825700), the Converging Research Center Program through the Ministry of Education, Science and Technology (2013K000307), ‘Establishment of National Physical Measurement Standards and Improvements of Calibration/Measurement Capability (grant no. 13011001)’of the Korea Research Institute of Standards and Science and Natural Science Foundation of China (grants 10979002 and 51371157) are gratefully acknowledged. The computer resources at the Shanghai Supercomputer Center and Westgrid in Canada are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
G.W.L., D.-H.K. and J.Z.J. designed the project. D.-H.K., H.B.Y. and H.H.L. performed and supported the experimental work. G.W.L., S.H.L. and D.-H.K. analysed the experimental data. H.Z., H.B.L. and X.D.W. performed simulations. H.Z., H.B.L., X.D.W., Q.P.C., D.X.Z. and J.Z.J. analysed the simulation data. G.W.L., D.-H.K. and J.Z.J. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supporting Online Material for Interfacial Free Energy Controlling Glass-Forming Ability of Cu-Zr Alloys
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Kang, DH., Zhang, H., Yoo, H. et al. Interfacial Free Energy Controlling Glass-Forming Ability of Cu-Zr Alloys. Sci Rep 4, 5167 (2014). https://doi.org/10.1038/srep05167
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05167
This article is cited by
-
Microstructures and properties of equiatomic CuZr and CuZrAlTiNi bulk alloys fabricated by mechanical alloying and spark plasma sintering
Journal of Materials Science (2017)
-
Manipulating the interfacial structure of nanomaterials to achieve a unique combination of strength and ductility
Nature Communications (2016)
-
Atomistic Design of Favored Compositions for Synthesizing the Al-Ni-Y Metallic Glasses
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.