Abstract
Emotion recognition through computational modeling and analysis of physiological signals has been widely investigated in the last decade. Most of the proposed emotion recognition systems require relatively long-time series of multivariate records and do not provide accurate real-time characterizations using short-time series. To overcome these limitations, we propose a novel personalized probabilistic framework able to characterize the emotional state of a subject through the analysis of heartbeat dynamics exclusively. The study includes thirty subjects presented with a set of standardized images gathered from the international affective picture system, alternating levels of arousal and valence. Due to the intrinsic nonlinearity and nonstationarity of the RR interval series, a specific point-process model was devised for instantaneous identification considering autoregressive nonlinearities up to the third-order according to the Wiener-Volterra representation, thus tracking very fast stimulus-response changes. Features from the instantaneous spectrum and bispectrum, as well as the dominant Lyapunov exponent, were extracted and considered as input features to a support vector machine for classification. Results, estimating emotions each 10 seconds, achieve an overall accuracy in recognizing four emotional states based on the circumplex model of affect of 79.29%, with 79.15% on the valence axis and 83.55% on the arousal axis.
Similar content being viewed by others
Introduction
The detection and recognition of emotional information is an important topic in the field of affective computing, i.e. the study of human affects by technological systems and devices1. Changes in emotional states often reflect facial, vocal and gestural modifications in order to communicate, sometimes sub-unconsciously, personal feelings to other people. Such changes can be generalized across cultures, e.g. nonverbal emotional, or can be culture-specific2. Since mood alteration strongly affects the normal emotional process, emotion recognition is also an ambitious objective in the field of mood disorder psychopathology. In the last decade, several efforts have tried to obtain a reliable methodology to automatically identify the emotional/mood state of a subject, starting from the analysis of facial expressions, behavioral correlates and physiological signals. Despite such efforts, current practices still use simple mood questionnaires or interviews for emotional assessment. In mental care, for instance, the diagnosis of pathological emotional fluctuations is mainly made through the physician's experience. Several epidemiological studies report that more than two million Americans have been diagnosed with bipolar disorder3 and about 82.7 million of the adult European population from 18 to 65 years of age, have been affected by at least one mental disorder4. Several computational methods for emotion recognition based on variables associated with the Central Nervous System (CNS), for example the Electroencephalogram (EEG), have been recently proposed5,6,7,8,9,10,11,12. These methods are justified by the fact that human emotions originate in the cerebral cortex involving several areas for their regulation and feeling. The prefrontal cortex and amygdala, in fact, represent the essence of two specific pathways: affective elicitations longer than 6 seconds allow the prefrontal cortex to encode the stimulus information and transmit it to other areas of the Central Autonomic Network (CAN) to the brainstem, thus producing a context appropriate response13; briefly presented stimuli access the fast route of emotion recognition via the amygdala. Of note, it has been found that the visual cortex is involved in emotional reactions to different classes of stimuli14. Dysfunctions on these CNS recruitment circuits lead to pathological effects15 such as anhedonia, i.e. the loss of pleasure or interest in previously rewarding stimuli, which is a core feature of major depression and other serious mood disorders.
Given the CAN involvement in emotional responses, an important direction for affective computing studies is related to changes of the Autonomic Nervous System (ANS) activity as elicited by specific emotional states. Monitoring physiological variables linked to ANS activity, in fact, can be easily performed through wearable systems, e.g. sensorized t-shirts16,17 or gloves18,46. Its dynamics is thought to be less sensitive to artifacting events than in the EEG case. Moreover, the human vagus nerve is anatomically linked to the cranial nerves that regulate social engagement via facial expression and vocalization. Engineering approaches to assess ANS patterns related to emotions constitute a relevant part of the state-of-the-art methods used in affective computing. For example, a recent review written by Calvo et al.19 reports on emotion theories as well as on affect detection systems using physiological and speech signals (also reviewed in20), face expression and movement analysis. Long multivariate recordings are currently needed to accurately characterize the emotional state of a subject. Such a constraint surely reduces the potential wide spectrum of real applications due to computational cost and number of sensors. More recently, ECG morphological analysis by Hilbert-Huang transform21, mutual information analysis of respiratory signals22 and a multiparametric approach related to ANS activity23 have been proposed to assess human affective states.
Experimental evidence over the past two decades shows that Heart Rate Variability (HRV) analysis, in both time and frequency domain, can provide a unique, noninvasive assessment of autonomic function24,25,88. Nevertheless, HRV analysis by means of standard procedures presents several limitations when high time and frequency resolutions are needed, due mainly to associated inherent assumptions of stationarity required to define most of the relevant HRV time and frequency domain indices24,25. More importantly, standard methods are generally not suitable to provide accurate nonlinear measures in the absence of information regarding phase space fitting. It has been well-accepted by the scientific community that physiological models should be nonlinear in order to thoroughly describe the characteristics of such complex systems. Within the cardiovascular system, the complex and nonstationary dynamics of heartbeat variations have been associated to nonlinear neural interactions and integrations occurring at the neuron and receptor levels, so that the sinoatrial node responds in a nonlinear way to the changing levels of efferent autonomic inputs27. In fact, HRV nonlinear measures have been demonstrated to be of prognostic value in aging and diseases24,25,26,28,29,30,31,32,33,34,35,36,41. In several previous works37,38,39,40,41,42,43, we have demonstrated how it is possible to estimate heartbeat dynamics in cardiovascular recordings under nonstationary conditions by means of the analysis of the probabilistic generative mechanism of the heartbeat. Concerning emotion recognition, we recently demonstrated the important role of nonlinear dynamics for a correct arousal and valence recognition from ANS signals44,45,46,71 including a preliminary feasibility study on the dataset considered here47.
In the light of all these issues, we here propose a new methodology in the field of affective computing, able to recognize emotional swings (positive or negative), as well as two levels of arousal and valence (low-medium and medium-high), using only one biosignal, the ECG and able to instantaneously assess the subject's state even in short-time events (<10 seconds). Emotions associated with a short-time stimulus are identified through a self-reported label as well as four specific regions in the arousal-valence orthogonal dimension (see Fig. 1). The proposed methodology is fully based on a personalized probabilistic point process nonlinear model. In general, we model the probability function of the next heartbeat given the past Revents. The probability function is fully parametrized, considering up to cubic autoregressive Wiener-Volterra relationship to model its first order moment. All the considered features are estimated by the linear, quadratic and cubic coefficients of the linear and nonlinear terms of such a relationship. As a consequence, our model provides the unique opportunity to take into account all the possible linear and nonlinear features, which can be estimated from the model parameters. Importantly as the probability function is defined at each moment in time, the parameter estimation is performed instantaneously, a feature not reliably accomplishable by using other more standard linear and nonlinear indices such as pNN50%, triangular index, RMSSD, Recurrence Quantification Analysis, etc.24,25,88. In particular, the linear terms allow for the instantaneous spectral estimation, the quadratic terms allow for the instantaneous bispectral estimation, whereas the dominant Lyapunov exponent can be defined by considering the cubic terms. Of note, the use of higher order statistics (HOS) to estimate our features is encouraged by the fact that quantification of HRV nonlinear dynamics play a crucial role in emotion recognition systems44,48,71 extending the information given by spectral analysis and providing useful information on the nonlinear frequency interactions.
A graphical representation of the circumplex model of affect with the horizontal axis representing the valence or pleasant dimension and the vertical axis representing the arousal or activation dimension49.
Results
Experimental protocol
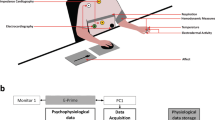
The recording paradigm related to this work has been previously described in44,48. We adopted a common dimensional model which uses multiple dimensions to categorize emotions, the Circumplex Model of Affects (CMA)49. The CMA used in our experiment takes into account two main dimensions conceptualized by the terms of valence and arousal (see Fig. 1). Valence represents how much an emotion is perceived as positive or negative, whereas arousal indicates how strongly the emotion is felt. Accordingly, we employed visual stimuli belonging to an international standardized database having a specific emotional rating expressed in terms of valence and arousal. Specifically, we chose the International Affective Picture System (IAPS)50, which is one of the most frequently cited tools in the area of affective stimulation. The IAPS is a set of 944 images with emotional ratings based on several studies previously conducted where subjects were requested to rank these images using the self assessment manikin (both valence and arousal scales range from 0 to 10). A general overview of the experimental protocol and analysis is shown in Fig. 2. The passive affective elicitation performed through the IAPS images stimulates several cortical areas also allowing the prefrontal cortex modulation generating cognitive perceptions13. An homogeneous population of 30 healthy subjects (aged from 21 to 24), not suffering from both cardiovascular and evident mental pathologies, was recruited to participate in the experiment. The experimental protocol for this study was approved by the ethical committee of the University of Pisa and an informed consent was obtained from all participants involved in the experiment. All participants were screened by Patient Health QuestionnaireTM (PHQ) and only participants with a score lower than 5 were included in the study51.
An overview of the experimental set-up and block scheme of the overall signal processing and classification chain.
The central nervous system is emotionally stimulated through images gathered from the International Affective Picture System. Such a standardized dataset associates multiple scores to each picture quantifying the supposed elicited pleasantness (valence) and activation (arousal). Accordingly, the pictures are grouped into arousal and valence classes, including the neutral ones. During the slideshow each image stands for 10 seconds, activating the prefrontal cortex and other cortical areas, consequently producing the proper autonomic nervous system changes through both parasympathetic and sympathetic pathways. Starting from the ECG recordings, the RR interval series are extracted by using automatic R-peak detection algorithms applied on artifact-free ECG. The absence of both algorithmic errors (e.g., mis-detected peaks) or ectopic beats in such a signal is ensured by the application of effective artifact removal methods as well as visual inspection. The proposed point-process model is fitted on the RR interval series and several features are estimated in an instantaneous fashion. Then, for each subject, a feature set is chosen and then split into training and test set for support vector machine-based classification. This image was drawn by G. Valenza, who holds both copyright and responsibility.
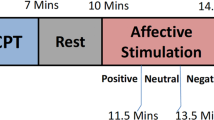
The affective elicitation was performed by projecting the IAPS images to a PC monitor. The slideshow was comprised of 9 image sessions, alternating neutral sessions and arousal sessions (see Fig. 3). The neutral sessions consist of 6 images having valence range (min = 5.52, max = 7.08) and arousal range (min = 2.42, max = 3.22). The arousal sessions are divided into Low-Medium (L-M) and Medium-High (M-H) classes, according to the arousal score associated. Such sessions include 20 images eliciting an increasing level of valence (from unpleasant to pleasant). The L-M arousal sessions had a valence range (min = 1.95, max = 8.03) and an arousal range (min = 3.08, max = 4.99). The M-H arousal sessions had a valence range (min = 1.49, max = 7.77) and an arousal range (min = 5.01, max = 6.99). The overall protocol utilized 110 images. Each image was presented for 10 seconds for a total duration of the experiment of 18 minutes and 20 seconds.
Sequence scheme over time of image presentation in terms of arousal and valence levels.
The y axis relates to the official IAPS score, whereas the x axis relates to the time. The neutral sessions, which are marked with blue lines, alternate with the arousal ones, which are marked with red staircases. Along the time, the red line follows the four arousal sessions having increasing intensity of activation. The dotted green line indicates the valence levels distinguishing the low-medium (L-M) and the medium-high (M-H) level within an arousing session. The neutral sessions are characterized by lowest arousal (<3) and medium valence scores (about 6).
During the visual elicitation, the electrocardiogram (ECG) was acquired by using the ECG100C Electrocardiogram Amplifier from BIOPAC inc., with a sampling rate of 250 Hz. A block diagram of the proposed recognition system is illustrated in Fig. 4. In line with the CMA model, the combination of two levels of arousal and valence brings to the definition of four different emotional states. The stimuli, with high and low arousal and high and low valence, produce changes in the ANS dynamics through both sympathetic and parasympathetic pathways that can be tracked by a multidimensional representation estimated in continuous time by the proposed point-process model. The obtained features are then processed for classification by adopting a leave-one-out procedure.
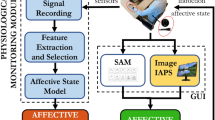
Logical scheme of the overall short-time emotion recognition concept.
The autonomic nervous system acts on the cardiovascular system modulating its electrical activity. This activity affects the heartbeat dynamics, which can be non-invasively revealed by the analysis and modeling of the RR interval series. To perform this task, we propose to consider a point-process probability density function in order to characterize cardiovascular dynamics at each moment in time. In particular, we use Wiener-Volterra nonlinear autoregressive integrative functions to estimate quantitative tools such as spectrum and bispectrum from the linear and nonlinear terms, respectively. Given the instantaneous spectra and high-order spectra, several features are combined to define the feature set, which is the input of the personalized pattern recognition procedure. Support vector machines are engaged to perform this task by adopting a leave-one-out procedure.
Algorithms
The ECG signal was analyzed off-line to extract the RR intervals24, then further processed to correct for erroneous and ectopic beats by a previously developed algorithm52. The presence of nonlinear behaviors in such heartbeat series was tested by using a well-established time-domain test based on high-order statistics53. The null hypothesis assumes that the time series are generated by a linear system. We set the number of laps to M = 8 and a total of 500 bootstrap replications for every test. Experimental results are shown in Table 1. The nonlinearity test gave significant results (p < 0.05) on 27 out of 30 subjects. In light of this result, we based our methodology on Nonlinear Autoregressive Integrative (NARI) models. Nonlinearities are intended as quadratic and cubic functions of the past RR intervals according to the Wiener-Volterra representation54,55. Major improvements of our approach rely on the possibility of performing a regression on the derivative RR series based on an Inverse Gaussian (IG) probability structure37,38,39. The quadratic nonlinearities contribute to the complete emotional assessment through features coming from the instantaneous spectrum and bispectrum56,57. It is worthwhile noticing that our feature estimation is derived from an equivalent nth-order inputoutput Wiener-Volterra model54,55, thus allowing for the potential estimation of the nth-order polyspectra of the physiological signal60 (see Materials and Methods section for details). Moreover, by representing the RR series with cubic autoregressive functions, it is possible to perform a further instantaneous nonlinear assessment of the complex cardiovascular dynamics and estimate the dominant Lyapunov exponent at each moment in time61. Indices from a representative subject are shown in Fig. 5. Importantly, the NARI model as applied to the considered data provides excellent results in terms of goodness-of-fit and independence test, with KS distances never above 0.056. A comparison analysis was performed between the simple linear and NARI models considering the Sum of the Squared Distances (SSD) of the points outside the confidence interval of the autocorrelation plot (see Table 1). We report that nonlinear point-process models resulted in lower SSD on all the considered subjects. Further results reporting the number of points outside the confidence interval of the autocorrelation plot are shown in the Supporting Information.
Instantaneous tracking of the HRV indices computed from a representative subject using the proposed NARI model during the passive emotional elicitation (two neutral sessions alternated to a L-M and a M-H arousal session).
In the first panel, the estimated μRR(t,  , ξ(t)) is superimposed on the recorded R-R series. Below, the instantaneous heartbeat power spectra evaluated in Low frequency (LF) and in High frequency (HF), the sympatho-vagal balance (LF/HF), several bispectral statistics such as the nonlinear sympathovagal interactions LL, LH and HH and the instantaneous dominant Lyapunov exponent (IDLE) are reported. In the three bottom panels, the tracking of emotion classification is shown in terms of arousal (A), valence (V) and their combination according to the circumplex model of affect (see Fig. 1). In such panels, the correct image classification is marked in red, whereas the misclassification is marked in blue. The neutral sessions are associated to the L-M arousal class exclusively without related valence class. This choice is justified as neutral stimuli could be arbitrarily associated to the L-M or M-H valence.
, ξ(t)) is superimposed on the recorded R-R series. Below, the instantaneous heartbeat power spectra evaluated in Low frequency (LF) and in High frequency (HF), the sympatho-vagal balance (LF/HF), several bispectral statistics such as the nonlinear sympathovagal interactions LL, LH and HH and the instantaneous dominant Lyapunov exponent (IDLE) are reported. In the three bottom panels, the tracking of emotion classification is shown in terms of arousal (A), valence (V) and their combination according to the circumplex model of affect (see Fig. 1). In such panels, the correct image classification is marked in red, whereas the misclassification is marked in blue. The neutral sessions are associated to the L-M arousal class exclusively without related valence class. This choice is justified as neutral stimuli could be arbitrarily associated to the L-M or M-H valence.
To summarize, the necessary algorithmic steps for the assessment of instantaneous ANS responses to short-time emotional stimuli are as follows: a) extract an artifact-free RR interval series from the ECG; b) use the autoregressive coefficients of the quadratic NARI expansion to extract the input-output kernels; c) estimate the instantaneous spectral and bispectral features; d) use the autoregressive coefficients of the cubic NARI expansion and fast orthogonal search algorithm to estimate the instantaneous dominant Lyapunov exponent. All the extracted instantaneous features (see Materials and Methods) are used as input of the classification procedure described below. Of note, since no other comparable statistical models have been advocated for a similar application, goodness-of-fit and classification performance of the proposed nonlinear approach are compared with its linear counterpart: the basic linear point-process model described in37, is also used here for the first time for the proposed classification analysis. Clearly, in order to perform a fair comparison, the order of such a simple linear IG-based point-process model was chosen considering an equal number of parameters that need to be estimated for the nonlinear models.
Moreover, here we report on the usability of other simple point-process models having the Poisson distribution as inter-beat probability. Such a model gave poor performances in terms of both goodness-of-fit and resulting in sufficient reliability to solve the proposed classification problems. All of the algorithms were implemented by using Matlab© R2013b endowed with self-made code and three additional toolboxes for pattern recognition and signal processing, i.e. LIBSVM62, PRTool63 and time series analysis toolbox64.
Classification
To perform pattern recognition of the elicited emotional states, a two-class problem was considered for the arousal, valence and self-reported emotion: Low-Medium (L-M) and Medium-High (M-H). The arousal classification was linked to the capability of our methodology in distinguishing the L-M arousal stimuli from the M-H ones, with the neutral sessions associated to the L-M arousal class. The overall protocol utilized 110 images. According to the scores associated to each image, for each subject, the dataset was comprised of 64 examples for the L-M arousal class and 40 examples for the M-H arousal class. Regarding valence, we distinguished the L-M from the M-H valence regardless of the images belonging to the neutral classes. This choice is justified by the fact that the neutral images can be equally associated to the L-M or M-H valence classes. According to the experimental protocol timeline, for each subject, the dataset was comprised of 40 examples for the L-M valence class and 40 examples for the M-H valence class. For the self-reported emotions, we used labels given by the self-assessment manikin (SAM) report. After the visual elicitation, in fact, each subject was asked to fill out a SAM test associating either a positive or a negative emotion to each of the seen images. During this phase, the images were presented in a different randomized order with respect to the previous sequence.
As a further challenge, a more difficult four-class problem was solved by defining the recognition of four different emotional states associated with specific regions of the arousal-valence plane. Specifically, given a selective combination of the L-M and M-H levels of the arousal and valence CMA dimensions, the following four emotional states were distinguished: “sadness”, as a simultaneous effect of L-M valence and L-M arousal; “anger”, as a simultaneous effect of L-M valence and M-H arousal; “happiness”, as a simultaneous effect of M-H valence and M-H arousal; “relaxation”, as a simultaneous effect of M-H valence and L-M arousal (see Fig. 1).
For each of the mentioned classification problems, a leave-one-out procedure91 was performed on the N available features using a well-known Support Vector Machine (SVM)66 as pattern recognition algorithm. Specifically, we used a nu-SVM (nu = 0.5) having a radial basis kernel function  with γ = N−1,
with γ = N−1,  as the training vectors. Results gathered from SVM classifiers are summarized in Tables 1 and 2 and reported as recognition accuracy, i.e. the percentage of correct classification among all classes for each subject and for each of the emotion classification cases.
as the training vectors. Results gathered from SVM classifiers are summarized in Tables 1 and 2 and reported as recognition accuracy, i.e. the percentage of correct classification among all classes for each subject and for each of the emotion classification cases.
All the estimated HRV indices coming from the NARI models were processed in order to define the whole feature set FNARI. Such a whole feature set is comprised of five linear-derived and eleven nonlinear-derived features. In this case, linear-derived means that such features, namely the mean and standard deviation of the IG distribution (corresponding to the instantaneous point process definitions of mean and standard deviation of the RR intervals37), the power in the low frequency (LF) band, the power in the high frequency (HF) band and the LF/HF ratio, are estimated having only knowledge of the linear coefficients of the models. Likewise, the nonlinear-derived features are estimated from the quadratic and cubic terms of the NARI model. In particular, features coming from the instantaneous bispectral analysis, namely the mean and the standard deviation of the bispectral invariants, mean magnitude, phase entropy, normalized bispectral entropy, normalized bispectral squared entropy, sum of logarithmic bispectral amplitudes and nonlinear sympatho-vagal interactions, are derived from the quadratic formulation (see Supporting Information), whereas the dominant Lyapunov exponents analysis was performed engaging cubic nonlinearities (see Materials and Methods).
In order to enhance the personalization of the system as well as improve the recognition accuracy, given the complete set FNARI, we further derived five subsets obtained by applying feature selection. Specifically, we defined the subset F1,NARI having the linear-derived features only, the subset F2,NARI having the linear-derived along with the nonlinear-derived bispectral features, the subset F3,NARI having the linear-derived features alongside the dominant Lyapunov exponent and the subset F4,NARI having the five most informative features as quantified through the Fisher score68. Of note, the sets verify the following relationships: F1,NARI ⊂ F2,NARI ⊂ FNARI; F1,NARI ⊂ F3,NARI ⊂ FNARI; F4,NARI ⊂ FNARI; firstly, we illustrate in Table 1 the classification results by comparing the performances of the reference linear point-process model with the NARI model with feature set giving the best recognition accuracy for each subject. The recognition accuracy of the short-term positive-negative self-reported emotions improves with the use of the nonlinear measures in 25 cases, with >60% of successfully recognized samples for all of the subjects and a maximum of 89.23% for subject 23. In 19 out of the 30 subjects the accuracies are >70% with a total average accuracy of 71.43% Concerning the L-M and M-H arousal classification, the recognition accuracy of the short-term emotional data improves in 24 cases, with >69.51% of successfully recognized samples for all of the subjects and a maximum of 95.12% for subject 22. In 29 out of the 30 subjects the accuracies are >70%, 23 of which are above 80%. The total average accuracy is 83.55%. Concerning the L-M and M-H valence classification, the recognition accuracy of the short-term emotional data is improved in 23 cases, with >65.38% of successfully recognized samples for all of the subjects and a maximum of 93.83% for subject 23. In 27 out of the 30 subjects the accuracy is >70%, 13 of which are above 80%. The total average accuracy is 79.15%.
Moreover, we show in Table 2 all the results obtained using the complete feature set FNARI. Although such a set might be not optimized, this choice allows for practical affective computing applications, possibly in real-time, retaining all of the information from both linear and nonlinear characteristics of the heartbeat complex dynamics. Alongside the separate arousal, valence and self-reported emotions, we also show the accuracy in recognizing the four emotional states defined in the arousal-valence plane. In this case, the recognition accuracy is >67.24% of successfully recognized samples for all subjects, with best performance for subject 23 (94.83%). In 27 out of the 30 subjects the accuracy is >70%, 14 of which are above 80%. The total average accuracy is 79.29%.
As a graphical representation of the results, Fig. 6 shows the complementary specificity-sensitivity plots for the three emotion classification cases. The complementary specificity is defined as (1-specificity), corresponding to the false positive rate. The area of the maximum rectangle that can be drawn within the lower-right unit plane not including any of the points (each representing the result from one subject) can be defined as the “maximum area under the points” (MAUP): the higher the MAUP, the greater the performance. The comparative evaluation of the maximum area under the points reveals that the point-process nonlinear (NARI) features give the best results on all the three emotion classification cases.
Complementary Specificity-Sensitivity Plots (CSSPs) for the three emotion classification cases.
In all panels, each blue circle represents a subject of the studied population, the x-axis represents the quantity 1-specificity (i.e. false positive rate) and the y-axis represents the sensitivity (i.e. true positive rate). The gray rectangles define the maximum area under the points. Numbers inside the rectangles indicate the maximum area under the points expressed as percentage of the unit panel area. On top, from left to right, the three panels represent the CSSPs obtained using features from the point process NARI model and considering the arousal, valence and self-reported emotion classification cases. Likewise, on the bottom, the three panels represent the CSSPs obtained using features from a point process linear model.
Other classification algorithms
The performances given by the proposed point process NARI model were also tested using the following six classification algorithms67: Linear Discriminant Classifier (LDC), Quadratic Discriminant Classifier (QDC), K-Nearest Neighborhood (KNN), MultiLayer Perceptron (MLP), Probabilistic Neural Network (PNN), Vector Distance Classifier (VDC). LDC and QDC are simple discriminant classifiers, i.e., there is no linear or nonlinear mapping of the feature set. Specifically, LDC finds the linear function that better discerns the feature space, whereas QDC finds the quadratic, thus nonlinear, one. MLP and PNN are common neural network-based algorithms performing a nonlinear mapping of the feature space and are able to find nonlinear functions discriminating the classes. KNN is a clustering algorithm through which the test set is associated to the most frequent class of the K nearest training examples. VDC is a KNN with K = 1.
Results showed that on the arousal classification, considering features coming from the point process NARI model the recognition accuracy of the short-term emotional data is improved as follows: 21 cases using LDC, 17 cases using QDC, 23 cases using KNN, MLP, PNN and VDC, among the total 30 cases. On the valence classification, considering features coming from the point process NARI model the recognition accuracy of the short-term emotional data is improved as follows: 24 cases using LDC, 18 cases using QDC and KNN, 27 cases using MLP, 22 cases using PNN and 23 cases using VDC, among the total 30 cases. On the self-reported emotion classification, considering features coming from the point process NARI model the recognition accuracy of the short-term emotional data is improved as follows: 21 cases using LDC, 18 cases using QDC and PNN, 22 cases using KNN, 24 cases using MLP and 19 cases using VDC, among the total 30 cases.
We also report that SVM algorithms always have the best recognition accuracy.
Discussion
We have presented a novel methodology able to assess in an instantaneous, personalized and automatic fashion whether the subject is experiencing a positive or a negative emotion. Assessments are performed considering only the cardiovascular dynamics through the RR interval series on short-time emotional stimuli (<10 seconds). To achieve such results, we defined an ad-hoc mathematical framework based on point-process theory. The point-process framework is able to parametrize heartbeat dynamics continuously without using any interpolation methods. Therefore, instantaneous measures of HR and HRV37,38 for robust short-time emotion recognition are made possible by the definition of a physiologically-plausible probabilistic model. An innovative aspect of the methodological approach is also the use of the derivative RR series69,70 to fit the model. This choice allowed us to remarkably improve the tracking of the affective-related, non-stationary heartbeat dynamics. The novel fully-autoregressive structure of our model accounts for the pioneering short-time affective characterization having knowledge related to both linear and nonlinear heartbeat dynamics. In fact, the quadratic and cubic autoregressive nonlinearities instantaneously associated to estimate the most likely heartbeat accounts for the estimation of high order statistics, such as the instantaneous bispectrum and trispectum, as well as significant complexity measures such as the instantaneous Lyapunov exponents. These novel instantaneous features, together with an effective protocol for emotion elicitation and the support of machine learning algorithms, allowed to successfully solve a comprehensive four-class problem recognizing affective states such as sadness, anger, happiness and relaxation.
Unlike other paradigms developed in the literature for estimating human emotional states19, our approach is purely parametric and the analytically-derived indices can be evaluated in a dynamic and instantaneous fashion. The proposed parametric model requires a preliminary calibration phase before it can be effectively used on a new subject. As the methodology is personalized, in fact, the model and classifier parameters have to be estimated using HRV data gathered during standardized affective elicitations whose arousal and valence scores lie on the whole CMA space. Moreover, a fine tuning of some of the model variables, e.g. the sliding time window W and the model linear and nonlinear orders, could be necessary to maximize the performance. Of note, considering short-time RR interval series gathered from 10 seconds of acquisition, currently used standard signal processing methods would be unable to give reliable and effective results because of resolution or estimation problems. In particular, parametric spectral estimation such as traditional autoregressive models would require interpolation techniques and would not give a goodness-of-fit measure, thus making the parameter estimation simply unreliable. In addition, non-parametric methods such as periodogram or Welch spectral estimation require stationarity and, considering the 10 second time window of interest, would give a frequency resolution of only 10−1 Hz which is not sufficient to reliably assess spectral powers up to the low frequency spectral components (0.04–0.15 Hz). Fast emotional responses, such as the ones considered in several recent studies13,14,97,98, call for estimation algorithms that can perform a reliable emotional assessment at time resolution as low as 2 seconds. In such cases, our methodology would be able to accurately characterize the emotional response by providing critical high resolution renditions. Accordingly, the methodology proposed here represents a pioneering approach in the current literature and can open new avenues in the field of affective computing, clinical psychology and neuro-economics.
Taking advantage of the standard subdivision in LF and HF frequency ranges in the bispectral domain (see Fig. 1 in the supporting information), our method introduces novel nonlinear indices of heartbeat dynamics directly related to higher order interactions between faster (vagal) and slower (sympatho-vagal) heartbeat variations, thus offering a new perspective into more complex autonomic dynamics. It has been demonstrated, in fact, that the cardiac and respiratory system exhibit complex dynamics that are further influenced by intrinsic feedback mechanisms controlling their interaction71. Cardio-respiratory phase synchronization represents an important phenomenon that responds to changes in physiological states and conditions, e.g. arousal visual elicitation48, indicating that it is strongly influenced by the sympatho-vagal balance72. We pointed out that lower performance was reported in seven subjects when using nonlinear models. This outcome is neither correlated with goodness-of-fit measures nor with the nonlinearity test results on the RR interval series. Possible explanations may span from confounding factors due to the fast protocol pace, to intrinsic individual characteristics of the emotional reaction to stimuli, or simple non-reported distraction from the task by the subject. Further investigations on these factors will be the subject of future studies. Since the proposed point-process framework allows the inclusion of physiological covariates such as respiration or blood pressure measures, future work will focus on further multivariate estimates of instantaneous indices such as features from the dynamic cross-spectrum, cross-bispectrum73, respiratory sinus arrhythmia39 and baroreflex sensitivity73 in order to better characterize and understand the human emotional states in short-time events. We will also direct our efforts in applying the algorithms to a wide range of experimental protocols in order to validate our tools for underlying patho-physiology evaluation, as well as explore new applications on emotion recognition that consider a wider spectrum of emotional states.
The primary impacts are in the affective computing field and in all the applications using emotion recognition systems. Our methodology, in fact, is able to assess the personal cognitive association related to a positive and a negative emotion with very satisfactory results. The emotional model used in this work, i.e., the CMA, accounts for the emotional representation by means of the selective estimation of arousal and valence. Although the recognition accuracy proposed in this work relates to only two levels of arousal, valence and self-reported emotion, oversimplifying the complete characterization of the affective state of a subject, the emotional assessment in short-time events using cardiovascular information only is a very challenging task never solved before. Using only heartbeat dynamics, we effectively distinguished between the two basic levels of both arousal and valence, thus allowing for the assessment of four basic emotions. An important advantage is that the proposed framework is fully personalized, i.e. it does not require data from a representative population of subjects. These achievements could have highly relevant impacts also in mood disorder psychopathology diagnosis and treatment, since the mood disorder produces an altered emotional response. Hence, monitoring fast emotional response in terms of stimulation time could make a continuous evaluation of disorder progression possible. Presently, emotional state is determined in a clinical setting using questionnaires with limited accuracy and quantitative power. It would be desirable to develop an automated system to determine and to quantify the emotional state. Doing this using a noninvasive physiological and easy-to-monitor signal such as the electrocardiogram, it would represent an important scientific advancement. From a physiological perspective, the inherent nonlinearties of the cardiovascular systems (e.g. the nonlinear neural signaling on the sinoatrial node27) have been also confirmed by our experimental results. According to the nonlinearity tests53, in fact, 27 out of the 30 RR series resulted to be the outputs of a nonlinear system. Of note, the results from goodness-of-fit tests were all positive, demonstrating that the proposed NARI model always performs a good prediction of the nonlinear heartbeat dynamics. We recently demonstrated the crucial role played by nonlinear dynamics in arousal and valence recognition starting from ANS signals44. In agreement with these previous results, here we have introduced instantaneous nonlinear features and improved the accuracy in the majority of the population (23 subjects) over the (also novel) results from the respective linear estimation. This finding is consistent with all the tested classification algorithms. A speculative explanation on the better performances obtained through ANS linear dynamics (observed in 7 subjects) can be related to the functional characteristics of the dynamical nonlinear vago-sympathetic interaction, i.e., the so-called bidirectional augmentation27. It is well-known, in fact, that the ANS control on the cardiovascular dynamics is based on the simultaneous activity and interaction of the sympathetic and vagal nerves. Sunagawa et al.27 showed that a perfect balance of these two neural activities leads to a linear control of the mean heart rate with a high potential dynamical gain (variance). On the other hand, when the sympathetic activity prevails on the parasympathetic one and vice versa, the cardiovascular control becomes nonlinear with a reduced dynamical gain. Changes on these time-varying nonlinear vago-sympathetic interactions follows a sigmoidal relationship between autonomic nerve activity and heart rate. Accordingly, it could be possible to hypothesize that the vago-sympathetic interactions of those 7 subjects showing a more linear ANS dynamics, when elicited with emotional images, are somehow more balanced than in the other subjects.
We also remark on the great improvement, over the random guess of 25%, performed by our methodology in recognizing four different emotional states during short-time stimuli. Such an achievement surely increases the impact in applicative fields such as affective computing, clinical psycology and neuro-economics. Moreover, our experimental results support previous studies where instantaneous HRV indices extracted by means of a point process model provided a set of dynamic signatures able to characterize the dynamic range of cardiovascular responses under different physiological conditions37. Therefore, the novel instantaneous nonlinear features could provide better assessment and improved reliability during such physiological responses.
Methods
The experimental protocol for this study was approved by the ethical committee of the University of Pisa and an informed consent was obtained from all participants involved in the experiment.
Nonlinear system identification and nonlinear autoregressive models
A Nonlinear Autoregressive Model (NAR) Model can be expressed, in a general form, as follows:

Considering  as independent, identically distributed Gaussian random variables, such a model can be can be written as a Taylor expansion:
as independent, identically distributed Gaussian random variables, such a model can be can be written as a Taylor expansion:

The autoregressive structure of (2) allows for system identification with only exact knowledge on output data and with only a few assumptions on input data. We represent here the nonlinear physiological system by using nonlinear kernels up to the second order, i.e. γ0, γ1(i) and γ2(i, j) and take into account the series of the derivatives in order to improve stationarity69,70. Hence, the general quadratic form of a Nonlinear Autoregressive Integrative (NARI) model becomes:

where Δy(k − i) = y(k − i) − y(k − i − 1) and Δy(k − j) = y(k − j) − y(k − j − 1). The quadratic kernel γ2(i, j) is assumed to be symmetric. We also define the extended kernels  and
and  as:
as:


and link the NARI model to a general input-output form, here defined by using the well-known Wiener-Volterra54 series:

where the functions hn(τ1, …, τn) are the Volterra kernels. Mapping a quadratic NARI model to an n-th order input-output model60 allows, after the input-output trasformation of the kernels, the evaluation of all the High Order statistics (HOS) of the system, such as the Dynamic Bispectrum and Trispectrum57,74. In the next paragraph, the definition of the generic variable y(k) is used to represent the first-moment statistic (mean) of the probabilistic generative mechanism of the heart rate. In other words, the generic formulation of the NARI model parametrizes the autonomic control on the cardiovascular system using linear and nonlinear terms according to the Wiener-Volterra representation and point-process theory.
Point-process nonlinear model of the heartbeat
The point process framework primarily defines the probability of having a heartbeat event at each moment in time. Such a probability accounts for the instantaneous estimation of features which are sensible to short-time emotional variations. Formally, defining t ∈ (0, T], the observation interval and  the times of the events, we can define N(t) = max{k : uk ≤ t} as the sample path of the associated counting process. Its differential, dN(t), denotes a continuous-time indicator function, where dN(t) = 1 when there is an event (the ventricular contraction), or dN(t) = 0 otherwise. The left continuous sample path is defined as
the times of the events, we can define N(t) = max{k : uk ≤ t} as the sample path of the associated counting process. Its differential, dN(t), denotes a continuous-time indicator function, where dN(t) = 1 when there is an event (the ventricular contraction), or dN(t) = 0 otherwise. The left continuous sample path is defined as  . Given the R-wave events
. Given the R-wave events  detected from the ECG, RRj = uj − uj−1 > 0 denotes the jth RR interval. Assuming history dependence, the inverse Gaussian probability distribution of the waiting time t − uj until the next R-wave event is37:
detected from the ECG, RRj = uj − uj−1 > 0 denotes the jth RR interval. Assuming history dependence, the inverse Gaussian probability distribution of the waiting time t − uj until the next R-wave event is37:

with  the index of the previous R-wave event before time
the index of the previous R-wave event before time  is the history of events, ξ(t) the vector of the time-varing parameters,
is the history of events, ξ(t) the vector of the time-varing parameters,  the first-moment statistic (mean) of the distribution and ξ0(t) > 0 the shape parameter of the inverse Gaussian distribution. Since
the first-moment statistic (mean) of the distribution and ξ0(t) > 0 the shape parameter of the inverse Gaussian distribution. Since  indicates the probability of having a beat at time t given that a previous beat has occurred at uj,
indicates the probability of having a beat at time t given that a previous beat has occurred at uj,  can be interpreted as the expected waiting time until the next event could occur. The use of an inverse Gaussian distribution
can be interpreted as the expected waiting time until the next event could occur. The use of an inverse Gaussian distribution  , characterized at each moment in time, is motivated both physiologically (the integrate-and-fire initiating the cardiac contraction37) and by goodness-of-fit comparisons39. In previous work38,39, the instantaneous mean
, characterized at each moment in time, is motivated both physiologically (the integrate-and-fire initiating the cardiac contraction37) and by goodness-of-fit comparisons39. In previous work38,39, the instantaneous mean  was expressed as a linear and quadratic combination of present and past R-R intervals, based on a nonlinear Volterra-Wiener expansion40. Here we propose the novel NARI formulation in which the instantaneous RR mean is defined as:
was expressed as a linear and quadratic combination of present and past R-R intervals, based on a nonlinear Volterra-Wiener expansion40. Here we propose the novel NARI formulation in which the instantaneous RR mean is defined as:

In this work, we consider nonlinearities associated to eq. 8 up to the third-order. Cubic terms, in fact, allow for the estimation of the dominant Lyapunov exponent, whereas quadratic terms account for the high-order spectral estimation. Considering the derivative RR interval series improves the achievement of stationarity within the sliding time window W (in this work we have chosen W = 70 seconds)69. Since  is defined in continuous time, we can obtain an instantaneous RR mean estimate at a very fine timescale (with an arbitrarily small bin size Δ), which requires no interpolation between the arrival times of two beats. Given the proposed parametric model, all linear and nonlinear indices are defined as a time-varying function of the parameters ξ(t) = [ξ0(t), γ0(t), γn(i1, …, in, t)] with n = {1, 2, 3}. The unknown time-varying parameter vector ξ(t) is estimated by means of a local maximum likelihood method37,75,76. The model goodness-of-fit is based on the Kolmogorov-Smirnov (KS) test and associated KS statistics (see details in37,77). Autocorrelation plots are considered to test the independence of the model-transformed intervals37. Optimal order of linear and nonlinear regressions is determined by prefitting the point process model to a subset of the data37,75 and comparing scores from KS tests, autocorrelation plots and the Akaike Information Criterion (AIC) which is defined as follows:
is defined in continuous time, we can obtain an instantaneous RR mean estimate at a very fine timescale (with an arbitrarily small bin size Δ), which requires no interpolation between the arrival times of two beats. Given the proposed parametric model, all linear and nonlinear indices are defined as a time-varying function of the parameters ξ(t) = [ξ0(t), γ0(t), γn(i1, …, in, t)] with n = {1, 2, 3}. The unknown time-varying parameter vector ξ(t) is estimated by means of a local maximum likelihood method37,75,76. The model goodness-of-fit is based on the Kolmogorov-Smirnov (KS) test and associated KS statistics (see details in37,77). Autocorrelation plots are considered to test the independence of the model-transformed intervals37. Optimal order of linear and nonlinear regressions is determined by prefitting the point process model to a subset of the data37,75 and comparing scores from KS tests, autocorrelation plots and the Akaike Information Criterion (AIC) which is defined as follows:

where L is the maximized value of the likelihood function for the estimated model, dim(ξ) is the number of parameters in the NARI model. We choose the parameter setup having the autocorrelation plot within the boundaries of 95% confidence interval and minimum AIC value and minimum KS distance. Once the order of linear and nonlinear regressions is determined, the initial NARI coefficients are estimated by the method of least squares78.
Estimation of the input-output volterra kernels
The nth-order spectral representations are related to the the Volterra series expansion and the Volterra theorem54. In functional analysis, a Volterra series denotes a functional expansion of a dynamic, nonlinear and time-invariant function, widely used in nonlinear physiological modeling55,79,80. The quadratic NARI model can be linked to the traditional input-output Volterra models by using a specific relationships60 between the Fourier transforms of the Volterra kernels of order p, Hp(f1, …, fn) and the Fourier transforms of the extended NAR kernels,  and
and  . In general, a second-order NARI model has to be mapped into a infinite-order input-output Volterra model60, although there is the need to truncate the series to a reasonable order for actual application. Here, we choose to model the cardiovascular activity with a cubic input-output Volterra by means of the following relationships with the NARI:
. In general, a second-order NARI model has to be mapped into a infinite-order input-output Volterra model60, although there is the need to truncate the series to a reasonable order for actual application. Here, we choose to model the cardiovascular activity with a cubic input-output Volterra by means of the following relationships with the NARI:



Quantitative tools: high order spectral analysis
Our framework allows for three levels of quantitative characterization of heartbeat dynamics: instantaneous time-domain estimation, linear power spectrum estimation and higher order spectral representation. The time-domain characterization is based on the first and the second order moments of the underlying probability structure. Namely, given the time-varying parameter set ξ(t), the instantaneous estimates of mean R-R, R-R interval standard deviation, mean heart rate and heart rate standard deviation can be extracted at each moment in time37. The linear power spectrum estimation reveals the linear mechanisms governing the heartbeat dynamics in the frequency domain. In particular, given the input-output Volterra kernels of the NARI model for the instantaneous R-R interval mean  , we can compute the time-varying parametric (linear) autospectrum81 of the derivative series:
, we can compute the time-varying parametric (linear) autospectrum81 of the derivative series:

where  . The time-varying parametric autospectrum of the R-R intervals is given by multiplying its derivative spectrum
. The time-varying parametric autospectrum of the R-R intervals is given by multiplying its derivative spectrum  by the quantity 2(1 − cos(ω))69. Importantly, previous derivations of the expressions for the autospectrum40,73 were possible because the first- and second-order Volterra operators are orthogonal to each other for Gaussian inputs. This property does not hold for orders greater than two81 and in cubic nonlinear input-output Volterra systems the autospectrum is estimated by considering also the third order term. By integrating (13) in each frequency band, we can compute the index within the very low frequency (VLF = 0.01–0.05 Hz), low frequency (LF = 0.05–0.15 Hz) and high frequency (HF = 0.15–0.5 Hz) ranges. The higher order spectral representation allows for consideration of statistics beyond the second order and phase relations between frequency components otherwise suppressed57,82. Higher order spectra (HOS), also known as polyspectra, are spectral representations of higher order statistics, i.e. moments and cumulants of third order and beyond. HOS can detect deviations from linearity, stationarity or Gaussianity. HOS analysis has been proven to be effective in several HRV applications (e.g. arrhythmia recognition58,59). Particular cases of higher order spectra are the third-order spectrum (Bispectrum) and the fourth-order spectrum (Trispectrum)82, defined from the Volterra kernel coefficients estimated within the point process framework.
by the quantity 2(1 − cos(ω))69. Importantly, previous derivations of the expressions for the autospectrum40,73 were possible because the first- and second-order Volterra operators are orthogonal to each other for Gaussian inputs. This property does not hold for orders greater than two81 and in cubic nonlinear input-output Volterra systems the autospectrum is estimated by considering also the third order term. By integrating (13) in each frequency band, we can compute the index within the very low frequency (VLF = 0.01–0.05 Hz), low frequency (LF = 0.05–0.15 Hz) and high frequency (HF = 0.15–0.5 Hz) ranges. The higher order spectral representation allows for consideration of statistics beyond the second order and phase relations between frequency components otherwise suppressed57,82. Higher order spectra (HOS), also known as polyspectra, are spectral representations of higher order statistics, i.e. moments and cumulants of third order and beyond. HOS can detect deviations from linearity, stationarity or Gaussianity. HOS analysis has been proven to be effective in several HRV applications (e.g. arrhythmia recognition58,59). Particular cases of higher order spectra are the third-order spectrum (Bispectrum) and the fourth-order spectrum (Trispectrum)82, defined from the Volterra kernel coefficients estimated within the point process framework.
Dynamical bispectrum estimation
Let H2(f1, f2, t) denote the Fourier transform of the second-order Volterra kernel coefficients. The cross-bispectrum (Fourier transform of the third-order moment) is56,57:

where  is the autospectrum of the input (i.e.
is the autospectrum of the input (i.e.  ). Note that we use the approximation shown in eq. 14 since the equality only strictly holds when the input variables are jointly Gaussian. The analytical solution for the bispectrum of a nonlinear system response with stationary, zero-mean Gaussian input is83:
). Note that we use the approximation shown in eq. 14 since the equality only strictly holds when the input variables are jointly Gaussian. The analytical solution for the bispectrum of a nonlinear system response with stationary, zero-mean Gaussian input is83:

Of note, an expression similar to 15 was derived in the appendix of84. The dynamic bispectrum is an important tool for evaluating the instantaneous presence of non-linearity in time series53,56,57. The bispectrum presents several symmetry properties82 and for a real signal it is uniquely defined by its values in the triangular region of computation Ω, 0 ≤ f1 ≤ f2 ≤ f1 + f2 ≤ 185. Within this region, it is possible to estimate several features, which are summarized in Table 1 of the supporting information. The bispectral invariant86, P(a, t) represent the phase of the integrated bispectrum along the radial line with the slope equal to a (with mean  and variance σP(a,t)). The parameter 0 < a ≤ 1 is the slope of the straight line on which the bispectrum is integrated. The variables Ir(a, t) and Ii(a, t) refer to the real and imaginary part of the integrated bispectrum, respectively. The Mean magnitude Mmean(t) and the phase entropy Pe(t)87 have n = 0, 1, …, N − 1; L as the number of points within the region Ω, Φ the phase angle of the bispectrum and 1(.) the indicator function which gives a value of 1 when the phase angle Φ is within the range of bin Ψn. The normalized bispectral entropy (P1(t))88 and the normalized bispectral squared entropy (P2(t))88 are also considered (between 0 and 1) along with the sum of logarithmic amplitudes of the bispectrum89. As the sympatho-vagal linear effects on HRV are mainly characterized by the LF and HF spectral powers24,90,92,93,94, we evaluate the nonlinerar sympatho-vagal interactions by integrating |B(f1, f2)| in the bidimensional combination of frequency bands. LL(t),LH(t) and HH(t) (see Supporting Information for a graphical representation in the bispectral plane).
and variance σP(a,t)). The parameter 0 < a ≤ 1 is the slope of the straight line on which the bispectrum is integrated. The variables Ir(a, t) and Ii(a, t) refer to the real and imaginary part of the integrated bispectrum, respectively. The Mean magnitude Mmean(t) and the phase entropy Pe(t)87 have n = 0, 1, …, N − 1; L as the number of points within the region Ω, Φ the phase angle of the bispectrum and 1(.) the indicator function which gives a value of 1 when the phase angle Φ is within the range of bin Ψn. The normalized bispectral entropy (P1(t))88 and the normalized bispectral squared entropy (P2(t))88 are also considered (between 0 and 1) along with the sum of logarithmic amplitudes of the bispectrum89. As the sympatho-vagal linear effects on HRV are mainly characterized by the LF and HF spectral powers24,90,92,93,94, we evaluate the nonlinerar sympatho-vagal interactions by integrating |B(f1, f2)| in the bidimensional combination of frequency bands. LL(t),LH(t) and HH(t) (see Supporting Information for a graphical representation in the bispectral plane).
Dynamical trispectrum estimation
Brillinger95, Billings54, Priestley96 and others have demonstrated that there is a closed form solution for homogeneous systems with Gaussian inputs. Thus, the transfer function of a m-order homogeneous system is estimated by the relation:

where the numerator is the m + 1 − nthorder crosspolyspectrum between y and x. This result is a generalization of the classical result for the transfer function of a linear system resulting for m = 1. Therefore, the cross-trispectrum (Fourier transform of the third-order moment) can be estimated as:

Dominant lyapunov exponent estimation
Cubic nonlinearities, in the framework of the proposed NARI point-process model, account for the novel estimation of the instantaneous Lyapunov spectrum. By definition, the generic Lyapunov exponent (LE) of a real valued function f(t) defined for t > 0 is defined as:

Let us consider a generic n-dimensional linear system in the form yi = Y (t) pi, where Y (t) is a time-varying fundamental solution matrix with Y (0) orthogonal and {pi} is an orthonormal basis of  . The key theoretical tools for determining the IDLE and the whole spectrum of LEs is the continuous QR factorization of Y (t)61,65:
. The key theoretical tools for determining the IDLE and the whole spectrum of LEs is the continuous QR factorization of Y (t)61,65:

where Q(t) is orthogonal and R(t) is upper triangular with positive diagonal elements Rii, 1 ≤ i ≤ n. Then, LEs are formulated as:

The cubic NAR model (eq. 8) can be rewritten in an M-dimensional state space canonical representation:

By evaluating the Jacobian J(n) over the time series, which corresponds to the matrix Y (t), the LE can be determined using the QR decomposition:

This decomposition is unique except in the case of zero diagonal elements. Then the LEs λi are given by

where H is the available number of matrices within the local likelihood window of duration W and τ the sampling time step. The estimation of the LEs is performed at each time t from the corresponding time-varying vector of parameters, ξ(t)61. Here, the first LE, λ1(t) is considered as the instantaneous dominant Lyapunov exponent (IDLE).
References
Picard, R. W. Affective computing (MIT Press, Boston, MA, 1997).
Sauter, D., Eisner, F., Ekman, P. & Scott, S. Cross-cultural recognition of basic emotions through nonverbal emotional vocalizations. P. Natl. Acad. Sci. USA 107, 2408–2412 (2010).
Kessler, R. et al. Lifetime and 12-month prevalence of dsm-iii-r psychiatric disorders in the united states: results from the national comorbidity survey. Arch. gen. psychiat. 51, 8 (1994).
Wittchen, H. & Jacobi, F. Size and burden of mental disorders in europe: a critical review and appraisal of 27 studies. Eur. neuropsychopharm. 15, 357–356 (2005).
Tang, Y. et al. Central and autonomic nervous system interaction is altered by short-term meditation. P. Natl. Acad. Sci. USA 106, 8865 (2009).
Petrantonakis, P. C. & Hadjileontiadis, L. J. Emotion Recognition From EEG Using Higher Order Crossings. IEEE T. Inf. Technol. B. 14, 186–197 (2010).
Ko, K. E., Yang, H. C. & Sim, K. B. Emotion recognition using EEG signals with relative power values and Bayesian network. Int. J. Control Autom. 7, 865–870 (2009).
Li, M., Chai, Q., Kaixiang, T., Wahab, A. & Abut, H. [EEG Emotion Recognition System.]. Vehicle Corpus and Signal Processing for Driver Behavior [Takeda, K. (ed.), Hansen, J. H. L. (ed.), Erdogan, H. (ed.), Abut, H. (ed.)] [125–135] (Springer, New York, 2009).
Lin, Y. P. et al. EEG-Based Emotion Recognition in Music Listening. IEEE T. Bio-Med Eng. 57, 1798–1806 (2010).
Petrantonakis, P. C. & Hadjileontiadis, L. J. A novel emotion elicitation index using frontal brain asymmetry for enhanced EEG-based emotion recognition. IEEE T. Bio-Med Eng. 15, 737–746 (2011).
Park, K. S. et al. Emotion recognition based on the asymmetric left and right activation. Int. J. Med. Medical Sci. 3, 201–209 (2011).
Hsieha, S., Hornbergera, M., Pigueta, O. & Hodges, J. R. Brain correlates of musical and facial emotion recognition: Evidence from the dementias. Neuropsychologia 50, 1814–1822 (2012).
Ruiz-Padial, E., Vila, J. & Thayer, J. The effect of conscious and non-conscious presentation of biologically relevant emotion pictures on emotion modulated startle and phasic heart rate. Int. J. Psychophysiol. 79, 341–346 (2011).
Tamietto, M. et al. Unseen facial and bodily expressions trigger fast emotional reactions. P. Natl. Acad. Sci. USA 106, 17661–17666 (2009).
Heller, A. et al. Reduced capacity to sustain positive emotion in major depression reflects diminished maintenance of fronto-striatal brain activation. P. Natl. Acad. Sci. USA 106, 22445–22450 (2009).
Valenza, G. et al. Wearable monitoring for mood recognition in bipolar disorder based on history-dependent long-term heart rate variability analysis. IEEE J. Biomed. Health Inform., (2014).
Valenza, G. et al. Mood recognition in bipolar patients through the PSYCHE platform: preliminary evaluations and perspectives. Artif. Intell. Med. 57, 49–58 (2013).
Lanata, A., Valenza, G. & Scilingo, E. P. A novel eda glove based on textile-integrated electrodes for affective computing. Med. Biol. Eng. Comput. 50, 1163–1172 (2012).
Calvo, R. & D'Mello, S. Affect detection: An interdisciplinary review of models, methods and their applications. IEEE T. Affect. Comp. 1, 18–37 (2010).
Koolagudi, S. G. & Rao, K. S. Recognition of Emotion from Speech: A Review. Int J Speech Technol 15, 99–117 (2012).
Agrafioti, F., Hatzinakos, D. & Anderson, A. Ecg pattern analysis for emotion detection. IEEE T. Affect. Comp. 3, 102–115 (2012).
Wu, C. K., Chung, P. C. & Wang, C. J. Representative Segment-based Emotion Analysis and Classification with Automatic Respiration Signal Segmentation. IEEE T. Affect. Comp. 3, 482–495 (2012).
Katsis, C. D., Katertsidis, N. S. & Fotiadis, D. I. An integrated system based on physiological signals for the assessment of affective states in patients with anxiety disorders. Biomed. Signal Proces. 6, 261–268 (2011).
Task Force of the European Society of Cardiology, the North American Society of Pacing and Electrophysiology, Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation 93, 1043–65 (1996).
Acharya, U. R., Joseph, K. P., Kannathal, N., Lim, C. & Suri, J. Heart rate variability: a review. Med. Biol. Eng. Comput. 44, 1031–1051 (2006).
Chua, C. K., Chandran, V., Acharya, U. R. & Lim, C. Application of higher order statistics/spectra in biomedical signals-A review. Med. Eng. Phys. 32, 679–689 (2010).
Sunagawa, K., Kawada, T. & Nakahara, T. Dynamic nonlinear vago-sympathetic interaction in regulating heart rate. Heart Vessels 13, 157–174 (1998).
Atyabi, F., Livari, M., Kaviani, K. & Tabar, M. Two statistical methods for resolving healthy individuals and those with congestive heart failure based on extended self-similarity and a recursive method. J. Biol. Phys. 32, 489–495 (2006).
Glass, L. Synchronization and rhythmic processes in physiology. Nature 410, 277–284 (2001).
Costa, M., Goldberger, A. & Peng, C. K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 89, 68102 (2002).
Poon, C. & Merrill, C. Decrease of cardiac chaos in congestive heart failure. Nature 389, 492–495 (1997).
Tulppo, M. et al. Physiological background of the loss of fractal heart rate dynamics. Circulation 112, 314 (2005).
Wu, G. et al. Chaotic signatures of heart rate variability and its power spectrum in health, aging and heart failure. PloS one 4, e4323 (2009).
Goldberger, A., Rigney, D. & West, B. Science in pictures: Chaos and fractals in human physiology. Sci. Am. 262, 42–49 (1990).
Sugihara, G., Allan, W., Sobel, D. & Allan, K. Nonlinear control of heart rate variability in human infants. P. Natl. Acad. Sci. USA 93, 2608 (1996).
Leistedt, S. J. J. et al. Decreased neuroautonomic complexity in men during an acute major depressive episode: analysis of heart rate dynamics. Translational Psych. 1, e27 (2011).
Barbieri, R., Matten, E., Alabi, A. & Brown, E. A point-process model of human heartbeat intervals: new definitions of heart rate and heart rate variability. Am. J. Physiol.-Heart C. 288, H424 (2005).
Barbieri, R. & Brown, E. Analysis of heartbeat dynamics by point process adaptive filtering. IEEE T. Bio-Med Eng. 53, 4–12 (2006).
Chen, Z., Brown, E. & Barbieri, R. Assessment of autonomic control and respiratory sinus arrhythmia using point process models of human heart beat dynamics. IEEE T. Bio-Med Eng. 56, 1791–1802 (2009).
Chen, Z., Brown, E. & Barbieri, R. Characterizing nonlinear heartbeat dynamics within a point process framework. IEEE T. Bio-Med Eng. 57, 1335–1347 (2010).
Valenza, G., Citi, L., Scilingo, E. P. & Barbieri, R. Point-Process Nonlinear Models with Laguerre and Volterra Expansions: Instantaneous Assessment of Heartbeat Dynamics. IEEE T. Signal Proces. 61, 2914–2926 (2013).
Valenza, G., Citi, L., Scilingo, E. P. & Barbieri, R. Using Laguerre expansion within point-process models of heartbeat dynamics: a comparative study. Paper presented at the International IEEE Engineering in Medicine and Biology Conference, San Diego CA, USA, IEEE 2012, August 28–September 1.
Valenza, G., Citi, L., Scilingo, E. P. & Barbieri, R. Instantaneous Bispectral Characterization of the Autonomic Nervous System through a Point-Process Nonlinear Model. Paper presented at the World Congress on Medical Physics and Biomedical Engineering, Beijing, China, (2012 May 21–31).
Valenza, G., Lanata, A. & Scilingo, E. P. The role of nonlinear dynamics in affective valence and arousal recognition. IEEE T. Affect. Comp. 3, 237–249 (2012).
Valenza, G., Allegrini, P., Lanata, A. & Scilingo, E. P. Dominant Lyapunov Exponent and Approximate Entropy in Heart Rate Variability during Emotional Visual Elicitation. Frontiers in Neuroeng. 5, 1–7 (2012).
Valenza, G., Lanata, A., Scilingo, E. P. & De Rossi, D. Towards a Smart Glove: Arousal Recognition based on Textile Electrodermal Response. Paper presented at the International IEEE Engineering in Medicine and Biology Conference, Buenos Aires, Argentina, IEEE (August 31–September 4).
Valenza, G., Citi, L., Lanata, A., Scilingo, E. P. & Barbieri, R. A Nonlinear Heartbeat Dynamics Model Approach for Personalized Emotion Recognition. Paper presented at International IEEE Engineering in Medicine and Biology Conference, Osaka, Japan, IEEE (2013 July 3–7).
Valenza, G., Lanata, A. & Scilingo, E. P. Oscillations of heart rate and respiration synchronize during affective visual stimulation. IEEE T. Inf. Technol. B. 16, 683 (2012).
Posner, J., Russell, J. & Peterson, B. The circumplex model of affect: An integrative approach to affective neuroscience, cognitive development and psychopathology. Dev. Psychopathol. 17, 715–734 (2005).
Lang, P., Bradley, M. & Cuthbert, B. International affective picture system iaps: Digitized photographs, instruction manual and affective ratings. Technical report A-6. Univ. Florida, (2005).
Kroenke, K., Spitzer, R. & Williams, J. The phq-9. J. Gen. Intern. Med. 16, 606613 (2001).
Citi, L., Brown, E. & Barbieri, R. A Real-Time Automated Point Process Method for Detection and Correction of Erroneous and Ectopic Heartbeats. IEEE T. Bio-Med Eng. 59, 2828–2837 (2012).
Barnett, A. & Wolff, R. A time-domain test for some types of nonlinearity. IEEE T. Signal Proces. 53, 26–33 (2005).
Billings, S. Identification of nonlinear system - a survey. Proc. IEEE 127, 272–285 (1980).
Marmarelis, V. Nonlinear dynamic modeling of physiological systems. (Wiley-IEEE Press, New York, 2004).
Nikias, C. & Mendel, J. Signal processing with higher-order spectra. IEEE Signal Proc. Mag. 10, 10–37 (1993).
Nikias, C. & Petropulu, A. Higher-order spectra analysis: A nonlinear signal processing framework. (PTR Prentice-Hall, Inc., New Jersey, USA, 1993).
Chua, K. C., Chandran, V., Acharya, U. R. & Lim, C. M. Cardiac state diagnosis using higher order spectra of heart rate variability. J. Med. Eng. Technol. 32, 145–155 (2008).
Lanata, A., Valenza, G., Mancuso, C. & Scilingo, E. P. Robust multiple cardiac arrhythmia detection through bispectrum analysis. Expert Syst. Appl. 38, 6798–6804 (2011).
Le Caillec, J. & Garello, R. Nonlinear system identification using autoregressive quadratic models. Signal Process. 81, 357–379 (2001).
Citi, L., Valenza, G. & Barbieri, R. Instantaneous estimation of high-order nonlinear heartbeat dynamics by Lyapunov exponents. Paper presented at International IEEE Engineering in Medicine and Biology Conference, San Diego, USA, IEEE (2012, August 28–September 1).
Chang, C. C. & Lin, C. J. LIBSVM: A library for support vector machines. ACM T. Intell. Syst. Tech. 2, 1–27 (2011). Software available at http://www.csie.ntu.edu.tw/cjlin/libsvm.
Van der Heijden, F., Duin, R. P. W., De Ridder, D. & Tax, D. M. J. Classification, parameter estimation and state estimation. (Wiley Online Library, New York, USA, 2004).
Schlogl, A. Time Series Analysis - A toolbox for the use with Matlab. Available online at http://pub.ist.ac.at/%7Eschloegl/matlab/tsa/ (Accessed: 18 February 2014).
Valenza, G., Citi, L. & Barbieri, R. Instantaneous Nonlinear Assessment of Complex Cardiovascular Dynamics by Laguerre-Volterra Point Process Models. Paper presented at International IEEE Engineering in Medicine and Biology Conference, Osaka, Japan, IEEE (2013 July).
Scholkopf, B., Smola, A., Williamson, R. & Bartlett, P. L. New support vector algorithms. Neural Comput. 12, 1207–124 (2000).
Duda, R., Hart, P. & Stork, D. G. Pattern classification. (John Wiley & Sons, New York, 2012).
He, X., Deng, C. & Partha, N. Laplacian score for feature selection. Adv. Neur. In. 18, 507–514 (2005).
Granger, C. & Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1, 15–29 (1980).
Chen, Z., Purdon, P., Brown, E. & Barbieri, R. A differential autoregressive modeling approach within a point process framework for non-stationary heartbeat intervals analysis. Paper presented at International IEEE Engineering in Medicine and Biology Conference, Buenos Aires, Argentina, IEEE (2010, August 31–September 4).
Valenza, G., Lanata, A. & Scilingo, E. P. Improving emotion recognition systems by embedding cardiorespiratory coupling. Physiol. Meas. 34, 449–464 (2013).
Bartsch, R., Schumann, A., Kantelhardt, J., Penzel, T. & Ivanov, P. Phase transitions in physiologic coupling. P. Natl. Acad. Sci. USA 109, 10181–10186 (2012).
Chen, Z. et al. Dynamic assessment of baroreflex control of heart rate during induction of propofol anesthesia using a point process method. Ann. Biomed. Eng. 39, 1–17 (2011).
Mendel, J. Tutorial on higher-order statistics (spectra) in signal processing and system theory: Theoretical results and some applications. Proc. IEEE 79, 278–305 (1991).
Loader, C. Local regression and likelihood. (Springer Verlag, Berlin, 1999).
Tibshirani, R. & Hastie, T. Local likelihood estimation. J. Am. Stat. Assoc. 82, 559–567 (1987).
Brown, E., Barbieri, R., Eden, U. & Frank, L. [Likelihood methods for neural spike train data analysis.]. Computational neuroscience: A comprehensive approach [Feng, J.] [253–286] (CRC Press, Boca Raton, Florida, 2003).
Westwick, D. & Kearney, R. Explicit least-squares methods, in Identification of nonlinear physiological systems. (Wiley-IEEE Press, New York, 2003).
Akay, M. Nonlinear Biomedical Signal Processing II: Dynamic Analysis and Modeling. (Wiley-IEEE Press, New York, 2000).
Jo, J. et al. A nonlinear model of cardiac autonomic control in obstructive sleep apnea syndrome. Ann. Biomed. Eng. 35, 1425–1443 (2007).
Koukoulas, P. & Kalouptsidis, N. Nonlinear system identification using gaussian inputs. IEEE T. Signal Proces. 43, 1831–1841 (1995).
Nikias, C. & Raghuveer, M. Bispectrum estimation: A digital signal processing framework. Proc. IEEE 75, 869–891 (1987).
Nichols, J., Olson, C., Michalowicz, J. & Bucholtz, F. The bispectrum and bicoherence for quadratically nonlinear systems subject to non- gaussian inputs. IEEE T. Signal Proces. 57, 3879–3890 (2009).
Caillec, J. & Garello, R. Asymptotic bias and variance of conventional bispectrum estimates for 2-d signals. Multidim. Syst. Sign. P. 16, 49–84 (2005).
Brillinger, D. & Rosenblatt, M. Asymptotic theory of estimates of kth-order spectra. P. Natl. Acad. Sci. USA 57, 206 (1967).
Chandran, V. & Elgar, S. Pattern recognition using invariants defined from higher order spectra-one dimensional inputs. IEEE T. Signal Proces. 41, 1, 205 (1993).
Ng, T., Chang, S. & Sun, Q. Blind detection of photomontage using higher order statistics. Paper presented at the International Symposium on Circuits and Systems, Vancouver, Canada, IEEE (2004 May 23–26).
Chua, K., Chandran, V., Acharya, U. & Lim, C. Application of higher order statistics/spectra in biomedical signals–a review. Med. Eng. Phys. 32, 679–689 (2010).
Zhou, S., Gan, J. & Sepulveda, F. Classifying mental tasks based on features of higher-order statistics from eeg signals in brain-computer interface. Inform. Sciences 178, 1629–1640 (2008).
Akselrod, S. [Components of heart rate variability: basic studies.]. Heart rate Variability [Malik, M. (ed.), Camm, A. J. (ed.)] [147–163] (Futura Publishing Company, New York, 1995).
Kearns, M. & Dana, R. Algorithmic stability and sanity-check bounds for leave-one-out cross-validation. Neural Comput. 11, 1427–1453 (1999).
Malliani, A. Association of heart rate variability components with physiological regulatory mechanisms. Heart rate Variability [Malik, M. (ed.), Camm, A. J. (ed.)] [173–188] (Futura Publishing Company, New York, 1995).
Malpas, S. Neural influences on cardiovascular variability: possibilities and pitfalls. Am. J. Physiol.-Heart C. 282, H6 (2002).
Ursino, M. & Magosso, E. Role of short-term cardiovascular regulation in heart period variability: a modeling study. Am. J. Physiol.-Heart C. 284, H1479 (2003).
Brillinger, D. The identification of polynomial systems by means of higher order spectra. J. Sound Vib. 12, 301–313 (1970).
Priestley, M. Spectral analysis and time series (Academic Press, London, UK, 1981).
Codispoti, M., Bradley, M. & Lang, P. J. Affective reactions to briefly presented pictures. Psychophysiology 38, 474–478 (2001).
Smith, J., Low, A., Bradley, M. & Lang, P. J. Rapid picture presentation and affective engagement. Emotion 6, 208–214 (2006).
Acknowledgements
The authors are grateful to Laura Maley for kindly reviewing the paper. The research leading to these results has received partial funding from the Department of Anesthesia, Critical Care & Pain Medicine, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA and European Union Seventh Framework Programme FP7/2007–2013 under grant agreement n 601165 of the project “WEARHAP” and under grant agreement ICT-247777 of the project “PSYCHE”.
Author information
Authors and Affiliations
Contributions
G.V., A.L. and E.S. designed the experiment, acquired and pre-processed the physiological data. G.V., L.C. and R.B. processed and analyzed the dataset using nonlinear point-process models. All authors wrote and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Valenza, G., Citi, L., Lanatá, A. et al. Revealing Real-Time Emotional Responses: a Personalized Assessment based on Heartbeat Dynamics. Sci Rep 4, 4998 (2014). https://doi.org/10.1038/srep04998
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04998
This article is cited by
-
Biomedical Signal Processing: The Cornerstone of Artificial Intelligence in Healthcare Wearables
Biomedical Materials & Devices (2022)
-
Separable convolutional neural networks for facial expressions recognition
Journal of Big Data (2021)
-
Assessing Autonomic Function from Electrodermal Activity and Heart Rate Variability During Cold-Pressor Test and Emotional Challenge
Scientific Reports (2020)
-
Long-term modulation of cardiac activity induced by inhibitory control over emotional memories
Scientific Reports (2020)
-
Analysis and classification of heart diseases using heartbeat features and machine learning algorithms
Journal of Big Data (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.