Abstract
The inner dynamics of the multiple actors of the informations systems – i.e, T.V., newspapers, blogs, social network platforms, – play a fundamental role on the evolution of the public opinion. Coherently with the recent history of the information system (from few main stream media to the massive diffusion of socio-technical system), in this work we investigate how main stream media signed interaction might shape the opinion space. In particular we focus on how different size (in the number of media) and interaction patterns of the information system may affect collective debates and thus the opinions' distribution. We introduce a sophisticated computational model of opinion dynamics which accounts for the coexistence of media and gossip as separated mechanisms and for their feedback loops. The model accounts also for the effect of the media communication patterns by considering both the simple case where each medium mimics the behavior of the most successful one (to maximize the audience) and the case where there is polarization and thus competition among media memes. We show that plurality and competition within information sources lead to stable configurations where several and distant cultures coexist.
Similar content being viewed by others
Introduction
Nowadays, there is an ongoing intense scientific debate around the definition of the foundational concepts as well as about the most appropriate methodological approaches to deal with the understanding of social dynamics1,2. However, the challenge of understanding human behavior remains complex and intricate. Humans are intentional (and not necessarily rational) and the their dynamics in the social space are influenced by the surrounding social context and by the information reported on the media. Tv, newspapers, blogs act on the memetic diffusion which, in turn, is affected by a massive amount of individual and social factors – e.g. tastes, desires, goals, trust, social pressure etc. To understand such mechanisms we have to consider several factors from how information is produced, up to how the various information sources interact within them (and with respect to the audience).
Media industries are influenced by business concentration and market segmentation, leading toward heightened oligopolistic competition, customized delivery of messages and vertical networking of the multimedia industry3,4,5.
In the traditional theory of political communication political influence through the media is largely determined by the interaction between the political elites (in their plurality) and professional journalists. Media act as gatekeepers of the information flows that shape public opinion6 then resulting in collective debates for the formation of the public opinion.
The recent transformation of the media environment results mainly in the fragmentation of the audience and the increasing control that new communication technologies give to the consumers of the media7,8.
Since such an interaction manifests in terms of production and selection of the proposed contents, we introduce a novel model of opinion dynamics on coupled and interacting networks. We stress the role of the media communication strategies by considering both the simple case where each media mimics the behavior of the most successful one – to maximize the audience – and the case where there is polarization and thus competition among media reported information – to preserve and satisfy the segmented audience and to follow the editorial line.
The increasingly massive use of Internet as a source of information and as a medium of communication has led to a shift of paradigm in the production/diffusion of contents as well as in the communication process. The debate about social relevant issues spreads and persists over the web by leading to the emergence of unprecedented social phenomena such as the massive recruitment of people around common interests, ideas or political visions9,10,11,12. In the past years an intensive research effort has been payed in understanding social phenomena from innovation diffusion, to social influence, up to opinions and their dynamics13,14,15,16,17,18,19,20,21,22,23; some of them have focused on the role of media24,25,26,27,28,29,30,31 and of the web32,33.
The interaction among media, with the advent of the WWW, has been subject to an important change: people are not passive anymore, but can be proactive to an extent that often main stream media acquire information directly by common people. Main stream media compete for the audience and therefore interact by adjusting their format/contents to collect the highest number of followers. Hence, if on the one hand people get informed by the media, on the other hand the information (as well as the way they are reported) are even more influenced by the evolution of the mass tastes. Media respond to the their editors which often are politically lined up and then we can have the emergence of monopoles (as in the case of regimes) or to polarized groups (as in the modern democracies) of information broadcasters aiming at influencing people toward one or another political party24,34. The aim of this work is a) to introduce in the field of opinion dynamics the role of the media dynamics as a results of a competition/imitation process which has the goal to reach the highest number of followers; b) to highlight the changes induced by the historical evolution of the information system from the traditional main stream media to the WWW and c) to study the effect of aggregation/fragmentation of opinions in mixed communication environment.
Since we want to stress the role of trust with respect to information available to an individual, we assume that the gossipers interact with their neighbors and with the media using the bounded confidence model (BCM)35 – i.e, only if the distance between their internal state (opinion) and the received information is below a given threshold σ (tolerance) they will be more likely to adjust their own opinion. The higher the tolerance, the more the people are likely to be influenced by (because they trust) the information circulating14,36,37.
On the other hand, the media aim to reach the highest number of followers, hence they change their message according to the attitude of the media with the highest number of followers. Finally, we introduce competition among media memes38,39 – i.e., we mark the edges between media with positive and negative values causing respectively to converge or diverge respect to their neighbor's attitudes. We show plurality and competition within the various information sources leads to stable configurations where several and distant cultures coexist coherently to the impressive multitude of debates occurring on socio-technical systems about different topics – e.g politics, economics or the he existence of chemical trails and reptilians, the new world order conspiracy and so forth).
Model
We model the information system and its inner dynamics on two different scenarios inspired by the shift of paradigm from the main stream media (when every medium knows about the format of all the others) and to the more recent advent of the socio-technical systems such as Facebook and Twitter (with more complicated connectivity patterns). The model accounts also for the effect of media communication patterns by considering both the simple case where each medium mimics the behavior of the most successful one (to maximize the audience) and the case where there is polarization and thus competition among media memes (to preserve their audience). Hence, the model discussed in this paper relies on two interacting networks: the media, which have the goal to collect the highest number of followers and the gossipers, which can acquire information both from other gossipers and by the media.
Even if usually an individual do not choose randamoly his information sources and his media exposure is opinion based40, for the sake of simplicity, we assume that the rate with which gossipers exchange opinions among themselves and consult the media are the same. At each time-step both gossipers and media can adjust their opinions (figure 1) and a selective choice of the media, at the level of the model, would just change the convergence times. Gossipers are likely to adjust their opinion only if the received information and their own beliefs are close enough, a situation referred as bounded confidence. Mathematical models of opinion dynamics under bounded confidence have been introduced by Axelrod in41 and then developed by Deffuant et al.35 and by Hegselmann and Krause42.
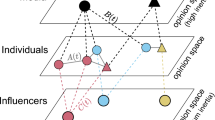
A graphical sketch of our model.
(Left panel) Gossipers interact among themselves choosing a neighbor in their social network (double arrow). If the gossipers have similar ideas, their opinion will converge further (eq.1). (Central panel) Gossipers are also influenced by the media: when they are exposed to information, their opinion will converge to such information if it is not too far from the gossiper's initial opinion (eq.2). (Right panel) Media are subject to a leader-follower dynamics. Media are supposed to have a network of other media with which interact either trying to copy their memes (black lines) or trying to oppose their memes (red dashed lines). Each media chooses to mimic/oppose the most successful (the one with more followers) of its neighboring media (eq.3). These drawings have been realized by AS using the open source clip-part collection at http://openclipart.org/.
Inspired by43 media are assumed to deliver information in a leader follower dynamics – i.e. to be audience oriented by mimicking the most successful medium in terms of number of customers.
The number of followers – i.e. individuals which accept the information reported on by the medium – is updated at each time step.
Each gossiper and media is initially assigned a random opinion described by a real value within a given opinion space [0..1]. We consider two interacting networks: the gossiper network Gg and the media network Gm. Gossipers interact through the bounded confidence model (BCM) of Deffuant and Weisbuch35 - i.e., at each time step t a gossiper i chooses at random a neighbor j in its social network and adjusts its opinion according to

where xi is the opinion of the gossipers i, μgg is a convergence factor, σgg is the threshold (opinion distance) above which gossipers do not interact and θ() is Heaviside's theta function.
We assume that also the interaction with the media has a BCM form:

Here k is a randomly chosen media, yk is the information (meme) reported by the k-th media, μgm is a convergence factor and σgm is the threshold below which gossipers gets influenced by the media.
The media choice at time t is described by the matrix  that is equals to 1 if the i-th gossiper has chosen the k-th media, 0 otherwise; i.e.
that is equals to 1 if the i-th gossiper has chosen the k-th media, 0 otherwise; i.e.  is a binary random variable that takes the value
is a binary random variable that takes the value  with probability 1/M and
with probability 1/M and  otherwise. We can therefore count the followers of each media as
otherwise. We can therefore count the followers of each media as

where ξt is calculated at each time-step.
We then introduce our max-audience oriented bounded confidence model among media interacting on a (possibly signed) network described by the matrix with elements Jkq ∈ {−1, 0, +1}. While the matrix |Jkq| correspond to the adjacency matrix of the network, the sign of Jkq indicates the polarization (friend/enemy) between the k-th and the q-the media. The case Jkq ≥ 0 corresponds to unpolarized media.
First, the meme of the k-th media is influenced by the most successful (the leader) l (k) of its neighbors neigh(k) = {q: |Jkq| > 0}

and then its meme is updated accorded a signed version of the BCM model:

where the function

constrains the memes in the interval [0, 1]. Notice that the use of periodic boundaries conditions is necessary as for Jkq < 0 the memes among the k-th and the q-th media tend to diverge and could therefore go below 0 or beyond 1. Moreover, using periodic boundary conditions avoids the problems of extremism (converge of opinions to 0 or 1) that can be induced by fixed boundary conditions44,45.
The convergence factors μαβ with α, β ∈ {g, m} correspond to the timescales of the dynamics. In our study, we always use μαβ = 0.3 and σgg = σgm = σmg = σ.
Since the opinion space [0, 1] is continuous, we can have different configuration in the final stationary opinion state. Opinions' clusters could be one (consensus), two (polarization), or more (fragmentation). In the following, we will first consider media as audience oriented agencies without any particular competition among them – i.e., a situation in which the opinion of a medium converges to the most successful among its' neighbors. Then, we will introduce competition among media memes – i.e., according to the structural balance of Heider46, we mark the edges between media with positive and negative values as in47,48,49 causing respectively a step toward or far from the most followed neighboring medium.
Results and Discussion
The analytical approach reveals that the our model is not amenable of a simple analytical solution not even at the mean-field level (see Methods for more details); therefore, we have resorted on numerical investigations. More precisely, we performed a thorough simulation program which considers different connectivity patterns for the two interacting layers acting on the opinion space (gossipers and media networks). We first show the opinion dynamics in the case where gossipers are subject to the audience oriented media broadcasting. Then, we introduce competition (polarization) in the media dynamics - i.e, each node of the media network, depending on the edge signature (positive or negative), can diverge (or converge) to (or from) the value of the most followed media. Accordingly to the information system historical evolution50,51,52 both the audience-oriented and the competing media cases are first considered in the complete graph case. This is the case of traditional main stream media where everybody knows about everybody. Finally, we consider the model's dynamics when nodes of the media networks are linked through more complex connectivity patterns like in the case of the WWW. The nodes of the gossipers network interact over a scale-free network generated with the Barabasi-Albert model53 that sets the exponent of the power law distribution to be 3.0. We explored also other connectivity patterns (Watts-Strogatz small world networks54 with different rewiring probability) noticing that the underlying topology does not affect the model qualitative behavior. We explore the model dynamics in terms of opinion distance and number of clusters as a function of the tolerance parameter. Each point of the parameter space (5000 steps) is averaged over 100 different possible initial configurations to attain the desired accuracy. When not specified, the size of the networks is to be assumed to be 104 nodes. The size of actors in traditional main-stream media (TMSM) is small: the number of televisions, radio stations, newspapers etc. allows everybody to check what the others are doing. For this reason, we will model interactions among the TMSM as a complete graph.
We first analyze the trend of opinions' extremal distances d – i.e., the distance between the highest and the lowest opinions in the gossipers' network – as a function of the tolerance σ. When d = 0, all the gossipers have reached consensus and share the same opinion while for d > 0, opinions are distributed; in the case of the standard BCM model, opinions are distributed in clusters (delta functions) separated by a distance higher than σ.
In Figure 2 we show the trend of the opinion distance (the highest opinion distance) as a function of the tolerance when the gossipers' network is scale-free53. We have checked that qualitatively similar results hold for the other gossip network topologies. It is known that the increasing of the tolerance parameter causes a reduction of the distance within opinions until it reduces to consensus – i.e, when the distance is 0 – and that the critical point (without media) is reached for value of tolerance of 0.555.
Maximal opinion distance d (the difference between the highest and lowest opinion in the gossipers' network) versus tolerance σ.
The size of the symbols is bigger than the error bars. Opinions' distance under the effect of audience-oriented unpolarized media shows a smoothening of the transition (less sharp change of d versus σ).
Here, we show that the media action smoothens the transition. In fact, the presence of the media as audience oriented information agencies can enlarge the transition area before the consensus to a single opinion. Such an effect is more evident for a small number of media. Under this settings media always reach a stationary state where they deliver the same message. The size only affects the time to converge. The imitation the most successful one triggers a leader-follower dynamics driven by the opinion clusters having the highest fraction of users. Such an interaction pattern produces conformity in the opinion space. Only when the time needed to the media to converge is lower than the time needed to the emergence of a dominant cluster in the opinion space, the media plays the role of an external field that smoothens the phase transition toward consensus.
In fact, the situation is completely different when we introduce competition (polarization) in the media information targeting mechanisms. With this feature media can have negative or positive feedbacks from the other media; therefore the most popular medium can cause either a convergence (positive coupling) or divergence (negative coupling) of its neighbors' memes. For the sake of simplicity we set to 0.5 the fraction of negative links of the media network – i.e, the number of links that will cause divergence with respect to the most followed media message.
To measure the possible sparsity of opinions induced by the negative links, we bin the opinion space in a probability vector φ and measure the localization parameter56:

If MB is the (large) number of bins of the probability vector, L ~ 1/MB ~ 0 if the opinions are evenly distributed, while L = 1 if all the opinions are concentrated in a single bin. In general, if opinions are evenly distributed in NC clusters, L−1 ~ NC is of the order of the number of different opinions.
The left panel of Figure 3 shows that for unsigned interactions among media, all the opinions converge to a single one, i.e. L = 1 for high values of σ. Notice that in the case of a large number of unpolarized media, two opinion clusters (L ~ 0.5) coexist at small σ's (roughly between σ = 0.05 and σ = 0.10). The smoothening effect of not competing media however is visible at low level of trust (small σs) where we observe a very short plateau. The right panel of Figure 3 shows a re-entrant effect in which the opinion space is highly fragmented for both low and high values of the tolerance σ. However, such fragmentation stems from different mechanisms; in fact, while at low σ opinion fragment into distinct non-interacting peaks as in the standard BCM, at high values of tolerance the opinions fragment because the competition among polarized memes. Low levels of trust in the circulating information allow for a broad distribution of the various opinions in the gossipers' ecosystem. Conversely, with increasing of trust, users are more prone to accept circulating memes that, in turn, lead to the formation of isolated clusters when their distribution is sparse. In fact, at high σ we find that while the average number of opinion peaks is stationary, their positions in the opinion space are dynamically fluctuating. Therefore, in the case of polarized media, even total trust in the information (σ = 1) does not produce full consensus as in the standard BCM, but induces a dynamically evolving stationary state in which users can still change their opinions.
Localization L versus tolerance σ.
Error bars are of the order of the symbol size. The localization parameter can be thought as the inverse of the number of different opinion; therefore L = 1 for consensus, while a low value of L signals fragmentation of the opinions. (Left panel) Localization in gossip scale-free networks increases with the tolerance when the media are audience oriented agencies (i.e. unpolarized). Notice that full consensus (L = 1) is reached at a tolerance ~ 0.5 like the single-network BCM model case. (Right panel) Localization has a non-monotonic trend when media are polarized; in particular, it reaches a maximum before the tolerance is maximal (σ = 1). Like in the BCM model, opinions are fragmented at low values of σ since they do not interact; unlike the BCM model, consensus is not reached at high values of σ and opinions are fragmented due to the polarization of the media.
The use of the Internet as a medium for sharing information has caused a shifting of paradigm from main stream centralized media to a more distributed and proactive protocol of information diffusion. At difference with traditional main-stream media, new media are composed of a large number of actors that cannot possibly check all the other media but that interact among each other through a social network. Hence, in this last scenario we use different topologies for the media network – i.e, of 104 nodes with scale-free and small-world topologies (the latter with rewiring probabilities p = 0.1, 0.2, 0.3) – acting on a gossip scale-free gossip network of the same size. We analyze both polarized (audience oriented) and unpolarized (competing) media; in the former case, for the sake of simplicity we set to 0.5 the fraction of negative links in the media network. Figure 4 shows the behavior of the localization for scale free media networks and small world topologies, both for the polarised and the unpolarised case. The high number of media makes extreme the effects evinced in the previous scenarios. However, the effects of the network structure is minor since curves for are qualitatively and quantitatively similar both for polarised and unpolarised media.
Localization L versus tolerance σ for Barabasi-Albert scale-free (BA) and Watts-Strogatz small world (WS) networks with rewiring probabilities p = 0.1, 0.2, 0.3.
Error bars are of the order of the symbol size. The complex networks of gossipers and media are of comparable sizes. (Left panel) For un-polarized media, increasing the tolerance leads toward consensus (L = 1). (Right panel) Polarization among the media produces a reentrant effect on the localization: while at low values of σ opinions are fragmented since they do not interact, at high values of the tolerance polarization induces fragmentation.
We observe that the result for new media are qualitatively similar to the ones for the traditional main-stream media: in both cases competition among the media (polarization) introduces a non monotonic behavior in opinions' fragmentation, gossipers never reach consensus and the minimum opinion spread is reached for values of tolerance σ < 1.
Despite different connectivity patterns – scale free AB networks are very different from the more clustered WS – the dynamics present a very similar behavior. They evolve with a similar pattern which – in the case of unpolarized media – presents a plateau at small value of σ due to the smoothening effect caused by the media which are deliverying competing messages with a small probability to affect users opinion. The different values of the clustering coefficient result in a small broadening in the opinions' distribution: the higher the clustering the larger the opinions' distribution. This is due to the formation of small groups on the same opinions which increases with the transitivity among gossipers.
Conclusions
In this paper we introduce a novel model of opinion dynamics accounting for the coexistence of media and of social influence as two separated but interdependent processes. People (nodes of the gossip network) interact with their neighbors or with the media using the Bounded Confidence Model (BCM)35 – i.e, only they will influence each other only if the distance between their opinions is below a given threshold σ (tolerance), the higher σ, the more people are likely to be influenced. In turn, the media (nodes of the media network) aim to capture the highest number of followers, hence they change their message by moving toward the value of the media with the highest number of followers. Finally, we introduce competition among media through polarization - i.e., media can interact with positive sign (their memes will converge) or negative sign (their memes will diverge).
We show that, when the media follow an audience oriented strategy of information delivery (i.e. everybody tries to mimic the most successful medium), there is a smoothening of consensus transition, indicating that the media messages tend to produce an impasse when amplified by the gossip dynamics. Such effect tends to disappear with increasing the number of media. On the other hand, competition (polarization) among media produces a fragmentation of the opinions' space thus preventing a system-wide consensus. Such scenario is qualitatively robust to changes in the topologies of the gossip-gossip and medium-medium interaction network; in particular, it stays true both for conventional media (where everybody can interact with everybody) and for new media (where interactions take the form of a social network). Finally, we notice that our choice of keeping equal the σ values is better suited to disentagle the contribution of the competition among the media to opinion fragmentation. Varying the tolerance parameters, other routes could be possible; as an example, a very small tolerance σmm among the media (conservative media) could keep opinions fragmented even for tolerances σgg among the gossipers beyond the consensus transition.
The next envisioned step will be to fine tune our model with real data from social networks platforms where main stream media directly interact with users and together change continuously the opinions' as well as the information space.
Methods
* Algorithm
The gossip network Gg = (Vg, Eg) is composed by N = |Vg| gossipers; the edges Eg represent social contacts among gossipers. Nodes of the gossip network interact with randomly selected a neighbor by applying the following rule: Given a node i that has selected a node j, having respectively opinion xi and xj (the opinion varies in a continuous space between 0.0 and 1.0)
for all i ∈ Vgdo
select random neighbor j
if
 then
then

where σgg is the threshold parameter (the distance between one is likely to consider the others opinions) and μgg is a convergence parameter varying in the interval (0, 1/2].
The media network Gm = (Vm, Em) is composed by M = |Vm| media and follows a similar rule except for the tolerance control. Each node α of the media network has an opinion yα selects in its neighborhood the one that has the highest number of followers (audience) and then apply the updating. Given two media i, j ∈ Vm
for all α ∈ Vmdo
select most influential neighbor β
if
 then
then

if
 then
then

if
 then
then

where Jαβ = ±1 represent the polarization among the media.
The set of edges Egm ⊂ Vg × Vm represents the media followed by the gossipers; i.e. an edge (i, α) ∈ Egm means that gossiper i can be influenced by the media α. The inter-network dynamics takes place by gossipers choosing at random a media among the ones they follow:
for all i ∈ Vgdo
select random media α
if
 then
then

Thus, each node of the gossip network talks with his friend and then gets informed by the media (by randomly selecting one node from the media network) In such a mechanism: a) a leader-follower dynamics emerges among media the messages delivered by the media; b) the gossip network and the media network have a feedback loop. Notice that we have checked that the update sequence does not influence the results of the dynamics.
* Mean field equations
A simple analytical tool that help to understand the main features of network-based models like our coupled BCM are the mean field (MF) approximations.
We will first sketch the MF solution in the general case of a BCM subject to a time dependent external field (information from the media). Let {xi} be the N opinions of the crowd and {yk} the M opinions (memes) of the media with xi, yk ∈ (0, 1). Let's suppose that at each step an individual i can get information by another randomly chosen person j with probability αg or by a randomly chosen media k with probability αm, with αi + αm = 1. The individual then gets influenced by the other opinion with probability cg (x, y) by individuals and cm (x, y) by media:

where cg and cm are functions that measure the interaction strenghts among different opinions. Notice that the standard BCM corresponds to αg = 1 and cg (x, y) = 1 − θ (σgg − |x − y|), where θ (x) is the Heavyside theta-function and σgg is the tolerance parameter of the BCM model. Let pg (x, t) and pm (x, t) be the probability distribution of individual opinions and of media opinions at time t. Rescaling the time by the average rate at which individuals receive informations, the evolution of the individual opinion distribution pg (x, t) is described by the master equation

Notice that in the BCM case with the standard choice μgg = 1/2, eq. 9 reduces to the MF equations

derived for the BCM model by Ben-naim and coauthors57. Let's now consider for simplicity the case in which cg (x, y) = cm (x, y) = 1 − θ (σ − |x − y|) and the distribution of media opinions is time independent. It is easy to check that to the field  with |yk − yl| > σ µk, l there corresponds the stationary solution pg (x) = pm (x). Notice that the MF approximation comes from disregarding joint correlations among the opinions, i.e.
with |yk − yl| > σ µk, l there corresponds the stationary solution pg (x) = pm (x). Notice that the MF approximation comes from disregarding joint correlations among the opinions, i.e.

We will now consider the general case in which the dynamics of the media is coupled to the dynamics of the opinions. Such a case can be described by adding to eq. 9 an equation for the field evolution

where in the MF approximation F is a functional of the pα only. For the media-media leader-follower dynamics, one has to understand which is the meme that has the maximum number of followers. Disregarding fluctuations, this can be calculated as

and the dynamics for the memes is

Eq. 13 makes the mean-field system of equation not amenable of simple solutions.
A further refinement of the MF approach would be needed in the case of competing media: in such a case, it is well known that even at the MF level more complicated techniques like the cavity method or the replica trick are needed to solve systems with competing interactions58,59.
References
Lazer, D. et al. Social science. computational social science. Int S Techn Pol Inn 323, 721–723 (2009).
Conte, R. et al. Manifesto of computational social science. EPJ ST 214, 325–346 (2012).
Croteau, D. & Hoynes, W. The Business of Media: Corporate Media and the Public Interest (SAGE Publications, 2006).
Deuze, M. Convergence culture in the creative industries. International J. Of Cultural Stud. 10, 243–263 (2007).
Hesserus, M. Snabbmatsradions uppkomst. Axess (2007).
Iyengar, S. Is anyone responsible? How television frames political issues (University of Chicago Press, Chicago, 1991).
Price, M., Noll, R. & Morrisett, L. A Communications Cornucopia: Markle Foundation Essays on Information Policy (Brookings Institution Press, 1998).
Jenkins, H. The Cultural Logic of Media Convergence. International J. Of Cultural Stud. 7, 33–43 (2004).
Guillory, J. et al. Upset now?: emotion contagion in distributed groups. In: Proceedings of the SIGCHI Conference on Human Factors in Computing Systems CHI' 11, 745–748 (ACM, New York, NY, USA, 2011).
Bekkers, V., Beunders, H., Edwards, A. & Moody, R. New media, micromobilization and political agenda setting: Crossover effects in political mobilization and media usage. INFORM SOC 27, 209–219 (2011).
González-Bailón, S., Borge-Holthoefer, J., Rivero, A. & Moreno, Y. The dynamics of protest recruitment through an online network. Sci Rep 1, (2011).
Garcia, D., Mendez, F., Serdült, U. & Schweitzer, F. Political polarization and popularity in online participatory media: an integrated approach. In: Proceedings of the first edition workshop on Politics, elections and data PLEAD' 12, 3–10 (ACM, New York, NY, USA, 2012).
Castellano, C., Fortunato, S. & Loreto, V. Statistical physics of social dynamics. Rev Mod Phys 81, 591+ (2009).
Lorenz, J. Continuous opinion dynamics under bounded confidence: A survey. Int J Mod Phys C 18, 1819–1838 (2007).
Paolucci, M. et al. Social Knowledge for e-Governance: Theory and Technology of Reputation (Roma: ISTC-CNR, 2009).
Nowak, A., Latane, B. & Szamrej, J. From private attitude to public opinion: A dynamic theory of social impact. Psychol Rev 97, 362–376 (1990).
Mason, W., Conrey, F. & Smith, E. Situating Social Influence Processes: Dynamic, Multidirectional Flows of Influence Within Social Networks. Pers Soc Psychol Rev 11, 279 (2007).
Lavine, H. & Latané, B. A cognitive-social theory of public opinion: Dynamic impact and cognitive structure. J Commun 46, 48–56 (1996).
Festinger, L., Schachter, S. & Back, K. Social Pressures in Informal Groups: A Study of Human Factors in Housing (Harper, 1950).
Masuda, N. & Redner, S. Can partisan voting lead to truth? J Stat Mech-theory E 2011, L02002 (2011).
Mccombs, M. E. & Shaw, D. L. The Agenda-Setting Function of Mass Media. PUBLIC OPIN QUART 36, 176–187 (1972).
Brunetti, S., Lodi, E. & Quattrociocchi, W. Dynamic monopolies in colored tori. In: Parallel and Distributed Processing Workshops and Phd Forum (IPDPSW), 2011 IEEE International Symposium on 626–631 (IEEE, 2011).
Brunetti, S., Cordasco, G., Gargano, L., Lodi, E. & Quattrociocchi, W. Minimum weight dynamo and fast opinion spreading. In: Graph-Theoretic Concepts in Computer Science 249–261 (Springer Berlin Heidelberg, 2012).
Quattrociocchi, W., Conte, R. & Lodi, E. Opinions manipulation: Media, power and gossip. Adv Complex Syst 14, 567–586 (2011).
Phillips, D. The impact of mass media violence on u.s. homicides. Am Sociol Rev 48, 560–568 (1983).
Knut, A. & Jacobsson, S. Political media contests and confirmatory bias. Research Papers in Economics 2002:3, Stockholm University, Department of Economics (2002).
Martins, T. V., Pineda, M. & Toral, R. Mass media and repulsive interactions in continuous-opinion dynamics. Europhys Lett 91, 48003 (2010).
Carletti, T., Fanelli, D., Grolli, S. & Guarino, A. How to make an efficient propaganda. Europhys Lett 2, 222–228 (2006).
Quattrociocchi, W., Paolucci, M. & Conte, R. On the effects of informational cheating on social evaluations: image and reputation through gossip. IJKL 5, 457–471 (2009).
Shibanai, Y., Yasuno, S. & Ishiguro, I. Effects of global information feedback on diversity: Extensions to axelrod's adaptive culture model. J CONFLICT RESOLUT 45, pp. 80–96 (2001).
Gonzalez-Avella, J. C., Cosenza, M. G., Eguiluz, V. M. & San Miguel, M. Spontaneous ordering against an external field in nonequilibrium systems. New J Phys 12, 013010+ (2008).
Ugander, J., Backstrom, L., Marlow, C. & Kleinberg, J. Structural diversity in social contagion. P Natl Acad Sci Usa (2012).
Borge-Holthoefer, J. et al. Structural and dynamical patterns on online social networks: The spanish may 15th movement as a case study. PLoS One 6, e23883 (2011).
Deighton, J. & Grayson, K. Marketing and seduction: Building exchange relationships by managing social consensus. J CONSUM RES 21, 660–76 (1995).
Deffuant, G., Neau, D., Amblard, F. & Weisbuch, G. Mixing beliefs among interacting agents. Adv Complex Syst 3, 87–98 (2001).
Dittmer, J. C. Consensus formation under bounded confidence. NONLINEAR ANAL-THEOR 47, 4615–4621 (2001).
Krawczyk, M. J., Malarz, K., Korff, R. & Kulakowski, K. Communication and trust in the bounded confidence model. In: Pan J.-S., Chen S.-M., & Nguyen N. T. (eds.) ICCCI (1), vol. 6421 of Lecture Notes in Computer Science 90–99 (Springer, 2010).
Adamic, L. & Glance, N. The political blogosphere and the 2004 u.s. election: Divided they blog. In: In LinkKDD'05: Proceedings of the 3rd international workshop on Link discovery 36–43 (2005).
Weng, L., Flammini, A., Vespignani, A. & Menczer, F. Competition among memes in a world with limited attention. Sci Rep 2, (2012).
An, J., Quercia, D. & Crowcroft, J. Fragmented social media: a look into selective exposure to political news. In: WWW (Companion Volume) 51–52 (2013).
Axelrod, R. The Dissemination of Culture: A Model with Local Convergence and Global Polarization. J. Conflict Resolut. 41, 203–226 (1997).
Hegselmann, R. & Krause, U. Opinion dynamics and bounded confidence: Models, analysis and simulation. J. Artif. Soc. Soc. Simulat 5, 1–24 (2002).
Marlow, C. The Structural Determinants of Media Contagion. phd, Massachusetts Institute of Technology, Cambridge, MA (2005).
Deffuant, G., Amblard, F., Weisbuch, G. & Faure, T. How can extremism prevail? a study based on the relative agreement interaction model. J. Artif. Soc. Soc. Simulat 5, (2002).
Gargiulo, F. & Mazzoni, A. Can extremism guarantee pluralism? J. Artif. Soc. Soc. Simulat 11, (2008).
Heider, F. Attitudes and cognitive organization. J Psych 21, 107–112 (1946).
Easley, D. & Kleinberg, J. Networks, Crowds and Markets: Reasoning About a Highly Connected World (Cambridge University Press, 2010).
Wasserman, S., Faust, K. & Iacobucci, D. Social Network Analysis: Methods and Applications (Structural Analysis in the Social Sciences) (Cambridge University Press, 1994).
Leskovec, J., Huttenlocher, D. & Kleinberg, J. Signed networks in social media. In: Proceedings of the SIGCHI Conference on Human Factors in Computing Systems CHI' 10, 1361–1370 (ACM, New York, NY, USA, 2010).
Scolari, C. Media evolution: Emergence, dominance, survival and extinction in the media ecology. Int. J. Comm. 7, 1418–1441 (2013).
Jenkins, H. Convergence Culture: Where Old and New Media Collide (NYU Press, New York, 2006).
Stober, R. What media evolution is: A theoretical approach to the history of new media. Eur J Commun 19, 483–505 (2004).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Int S Techn Pol Inn 286, 509–512 (1999).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440 (1998).
Fortunato, S. Universality of the Threshold for Complete Consensus for the Opinion Dynamics of Deffuant et al. Int J Mod Phys C 15, 1301–1307 (2004).
Nagel, S. R., Grest, G. S. & Rahman, A. Phonon localization and anharmonicity in model glasses. Phys Rev Lett 53, 368–371 (1984).
Ben-Naim, E., Krapivsky, P. L., Vazquez, F. & Redner, S. Unity and discord in opinion dynamics. Physica A (2003).
Mézard, M., Parisi, G. & Virasoro, M. A. Spin Glass Theory and Beyond (Singapore: World Scientific, 1987).
Mézard, M. & Parisi, G. The cavity method at zero temperature. J Stat Phys 111, 1–34 (2003).
Acknowledgements
We thank US grant HDTRA1-11-1-0048, CNR-PNR National Project “Crisis-Lab” and EU FET project MULTIPLEX nr.317532. The contents of the paper do not necessarily reflect the position or the policy of funding parties.
Author information
Authors and Affiliations
Contributions
A.S. and W.Q. equally contributed to the simulations and the data analysis. A.S., W.Q. and G.C. equally contributed to the writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Quattrociocchi, W., Caldarelli, G. & Scala, A. Opinion dynamics on interacting networks: media competition and social influence. Sci Rep 4, 4938 (2014). https://doi.org/10.1038/srep04938
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04938
This article is cited by
-
Cross-platform social dynamics: an analysis of ChatGPT and COVID-19 vaccine conversations
Scientific Reports (2024)
-
Anti-stigma narratives and emotional comfort against health crisis: a context analysis of UGC short videos from patients with COVID-19 infections
Scientific Reports (2023)
-
Analyzing the changing landscape of the Covid-19 vaccine debate on Twitter
Social Network Analysis and Mining (2023)
-
Perturbed Anisotropic Opinion Dynamics with Delayed Information
Journal of Statistical Physics (2023)
-
Using sentiment analysis to predict opinion inversion in Tweets of political communication
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.