Abstract
Current-induced spin polarization (CISP) on the outermost surfaces of Au, Cu, Pt, Pd, Ta and W nanoscaled films were studied using a spin-polarized positron beam. The Au and Cu surfaces showed no significant CISP. In contrast, the Pt, Pd, Ta and W films exhibited large CISP (3~15% per input charge current of 105 A/cm2) and the CISP of Ta and W were opposite to those of Pt and Pd. The sign of the CISP obeys the same rule in spin Hall effect suggesting that the spin-orbit coupling is mainly responsible for the CISP. The magnitude of the CISP is explained by the Rashba-Edelstein mechanism rather than the diffusive spin Hall effect. This settles a controversy, that which of these two mechanisms dominates the large CISP on metal surfaces.
Similar content being viewed by others
Introduction
Spintronics, which aims to produce, inject, transport, manipulate and detect the electron spins, is promising to go beyond the traditional charge-based electronics1. Current-induced spin polarization (CISP) plays a critical role in spintronics. The spin Hall effect (SHE) and the Rashba effect are the representative phenomena producing CISP.
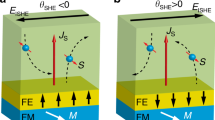
In the SHE, a finite spin current appears due to the charge current and the spin-orbit coupling (SOC). The efficiency of charge-to-spin conversion is defined as the ratio of spin to charge current densities (θSH = js/jc, called spin Hall angle). At sample edges, opposite electron spins are accumulated. Large spin Hall effects have been found in metallic thin films of Pt2, Pd3, β-Ta4 and β-W5.
The Rashba effect induces in-plane spin polarization in a two-dimensional electron gas (2DEG) system through the out-of-plane electric field and the SOC6. The strength of the Rashba effect is characterized by the energy splitting of up and down spin bands. The Rashba splitting energy observed for semiconductor heterostructure is only a few meV. Recently, so-called giant Rashba effects (of the order of 100 meV) have been reported for bulk Ir(111)7, Bi/Ag(111) surface alloy8 and Pb/Ag(111) surface alloy9.
It is still under debate that, which of the above two mechanisms is responsible for the large CISP on metal surfaces and interfaces. To solve this issue, surface sensitive probes are needed. Magneto-optical Kerr effect magnetometry is used for the observation of SHE in semiconductors10. However, this technique is not applicable to metallic thin films with thickness ranging from several nm to a few tens of nm. Spin-polarized positron beam is a promising new tool for such a purpose. Positronium (Ps), which is a bound state of a positron and an electron, is formed at the outermost surface of a metal11. From the spin-dependence of Ps formation and annihilation, the spin polarization of metal surface can be determined12. Recently, we reported the observation of the CISP on Pt surfaces13 by this technique. However, the origin of the observed CISP was not clarified. In the present study, we systematically investigate CISP in some other 4d and 5d transition metals. Consequently, we found that the CISP on these metal surfaces is explained in terms of the Rashba-Edelstein mechanism.
Results
Experimental setup and the principle
Figure 1 shows a schematic diagram of the experimental setup. The transversely spin-polarized positron beam, which was generated by a 22Na source (370 MBq) and an electrostatic apparatus, was implanted into the center of the sample14. The diameter and the spin polarization (P+) of the positron beam were 1 mm and 0.3, respectively. The beam energy (E+) was adjusted from 50 eV to 12 keV. The sample center was electrically grounded. Reversible currents (±jc) were applied to the samples through the two edges. The direct current was perpendicular to P+. A high purity Ge detector was placed perpendicular to the beam axis to record the annihilation γ ray spectra.
Spin-polarized slow (low energy) positrons injected into a metallic thin film could lead to a remarkable formation of Ps by picking up the electrons on the outermost surface. The formation probability of ortho-Ps ( ), which is influenced by the spin polarization of the outermost surface electrons (P−), could be derived from the positron annihilation γ ray spectra as the Ratio between the intensity of the low energy region and the 511 keV peak region (denoted as R). A function ΔR is defined to quantitatively characterize the
), which is influenced by the spin polarization of the outermost surface electrons (P−), could be derived from the positron annihilation γ ray spectra as the Ratio between the intensity of the low energy region and the 511 keV peak region (denoted as R). A function ΔR is defined to quantitatively characterize the  (details shown in the section of methods):
(details shown in the section of methods):

where R and R0 are derived from the γ ray spectra measured at E+ = 50 eV and 12 keV, respectively. The component of surface spin polarization along y axis (P−cosϕ) is calculated by

where ϕ is the relative angle of P− to P+ (y axis),  and
and  correspond to an input charge current density of +jc and −jc, respectively.
correspond to an input charge current density of +jc and −jc, respectively.
Experiments
All films were deposited by magnetron sputtering on different substrates (10 × 20 × 0.5 mm) at various growth temperatures. The details of the films are listed in Table 1. The thickness of Fe seed layer for Au film was 1 nm. The low resistivity (α phase: bcc structure) Ta and W films were grown on Al2O3(0001) substrates and the high resistivity (β phase: A15 structure) Ta and W films were grown on 100 nm thick SiO2 layers. The Au, Pt, Pd, α-Ta and α-W films were single crystals, which were confirmed by observing the reflection high energy electron diffraction patterns. The Cu, β-Ta and βα-W (a mixture of β and α phases in which β is dominant) films were polycrystals. The XRD patterns shown in Fig. 2 confirmed the α-Ta, β-Ta, α-W and βα-W films15,16,17. At least two samples were subjected to the CISP measurement for each film.
Input charge current densities jc are also listed in Table 1. To suppress the Joule heating, the applied electric powers were regulated to be less than 3 watts and the temperature was measured to be lower than 150°C. In this temperature range, fast Ps with the maximum energy of its work function (ΦPs ≈ 0.7 eV (Au), 2.5 eV (Cu), 2.9 eV (Pt), 0.4 eV (Pd), 4.0 eV (Ta(111)), 4.9 eV (W(111))) will be predominant over the thermal (~ 100 meV) Ps18,19,20,21. Therefore, positrons will pick up surface electrons with the energy from EF (Fermi level) to EF − ΦPs.
Material dependence of CISP
Figure 3 shows ΔR ( ) upon successive current reversal (+jc ↔ −jc) of all the films. For the Au and Cu films, no regular changes of ΔR upon current reversal could be seen. In contrast, the Pt, Pd, Ta and W surfaces show clear oscillations of ΔR. In addition to this, the ΔR oscillations of Ta and W films are opposite to those of Pt and Pd films. These results suggest that the CISP on the Au and Cu surfaces are rather small (
) upon successive current reversal (+jc ↔ −jc) of all the films. For the Au and Cu films, no regular changes of ΔR upon current reversal could be seen. In contrast, the Pt, Pd, Ta and W surfaces show clear oscillations of ΔR. In addition to this, the ΔR oscillations of Ta and W films are opposite to those of Pt and Pd films. These results suggest that the CISP on the Au and Cu surfaces are rather small ( ), while significant CISP are induced on the Pt, Pd, Ta and W surfaces. Also, the CISP on Ta and W surfaces are opposite to those on Pt and Pd surfaces. The transverse spin polarizations (P−cosϕ) estimated by Eq. (2) are listed in Table 1.
), while significant CISP are induced on the Pt, Pd, Ta and W surfaces. Also, the CISP on Ta and W surfaces are opposite to those on Pt and Pd surfaces. The transverse spin polarizations (P−cosϕ) estimated by Eq. (2) are listed in Table 1.
Figure 4 shows P−cosϕ per input charge current of jc = 1.0 × 105 A/cm2. The absolute values of P−cosϕ for the β-Ta and βα-W surfaces are 3 ~ 5 times greater than those for the Pt and Pd surfaces. For both high resistivity Ta and W films, P−cosϕ are significantly bigger than those of low resistivity Ta and W films.
Discussion
Table 2 lists the θSH of undoped metals obtained by different experimental methods. The values of θSH are rather scattered. Even for Pt, which is the most commonly studied spin Hall material, θSH varies between 0.37% and 11.0%. The Pt, Pd and Au films have positive θSH, while the Ta and W films have negative θSH. Furthermore, absolute values of θSH of Ta and W tend to be greater than those of Pt and Pd. The magnitudes of θSH of β phase Ta and W films have been reported to be much bigger than those in α phases4,5. These observations of θSH are mostly supported by theoretical studies of θSH in which the sign is positive (negative) if the outermost d-shell is more (less) than half filling30,31.
The sign and relative magnitude of the CISP observed for the Pt, Pd, Ta and W surfaces are in good agreement with those of θSH listed in Table 2. This reveals that the observed CISP for these surfaces are due to the SOC that is similar to SHE. According to the spin diffusion theory32, the energy width of polarized electrons in the density of states is given by the shift of chemical potential: Δµ = 2θSHλSjcρ, where λS is the spin diffusion length. For θSH = 10%, λS = 10 nm, ρ = 50 µΩcm and jc = 1.0 × 105 A/cm2, one finds Δµ = 1 µeV. The typical density of states at EF is 1023 cm−3eV−1 and hence the accumulated spin density will be 1017 cm−3. Assuming that positrons pick up electrons located from EF to EF−1 eV, the observable electron spin polarization will be ~10−4%. Therefore, the huge CISP observed above is hardly explained in terms of the diffusive SHE. More specific aspects of the surfaces should be considered.
Recently, the so-called giant Rashba effect has been reported for heavy metal surfaces7,8,9. The largest Rashba effects are five orders of magnitude greater than that estimated from the free electron model. Such a giant Rashba effect is explained by considering both strong SOC and steep gradient of electric potential near the surface. The spin density 〈δsy〉 induced by the Rashba effect is given by

where e is the elementary charge, D2D is the two-dimensional density of states, E is the applied electric field, τ is the electron relaxation time and αR is the Rashba parameter (Rashba-Edelstein model)33,34. Assuming αR = 3 × 10−10 eVm, D2D = 1014 cm−2eV−1, τ = 10 ps, E = 1 kV/m, one finds the spin polarization of the order of 5%. Thus, if the relaxation time is long enough, the above-observed huge CISP can be explained.
A recent study reported the spin-to-charge conversion at Bi/Ag interface, which is a well-known giant Rashba system35. The spin density and the two-dimensional charge current density  at an interface are related through
at an interface are related through  , which is essentially the same as Eq. (3). In the above study, excess spins of 〈δsy〉 = 2 × 107 cm−2 supplied to the Bi/Ag interface by the spin pumping induced
, which is essentially the same as Eq. (3). In the above study, excess spins of 〈δsy〉 = 2 × 107 cm−2 supplied to the Bi/Ag interface by the spin pumping induced  . In the Ag layer, the spin-to-charge conversion was negligible and independent of its thicknesses (5 to 20 nm). This would manifest that the spin-to-charge conversion was induced by an inverse Rashba effect but not inverse SHE. If we adopt this conversion efficiency in the present experiments, the two-dimensional charge current density
. In the Ag layer, the spin-to-charge conversion was negligible and independent of its thicknesses (5 to 20 nm). This would manifest that the spin-to-charge conversion was induced by an inverse Rashba effect but not inverse SHE. If we adopt this conversion efficiency in the present experiments, the two-dimensional charge current density  (0.05 to 0.5 A/cm) will generate excess surface spins of 〈δsy〉 = 1012 cm−2 at maximum. Thus, assuming again D2D = 1014 cm−2eV−1, one finds the spin polarization of 1%. This is comparable orders of magnitude as the above estimation using Eq. (3) in spite of many differences in experimental conditions. The αR and θSH are related via
(0.05 to 0.5 A/cm) will generate excess surface spins of 〈δsy〉 = 1012 cm−2 at maximum. Thus, assuming again D2D = 1014 cm−2eV−1, one finds the spin polarization of 1%. This is comparable orders of magnitude as the above estimation using Eq. (3) in spite of many differences in experimental conditions. The αR and θSH are related via  36. This may be the reason why the sign and the relative magnitude of the CISP observed here are in good agreement with those of θSH.
36. This may be the reason why the sign and the relative magnitude of the CISP observed here are in good agreement with those of θSH.
Furthermore, besides the Rashba effect at the outermost surface, one may naturally expect that the metal/substrate interface could also contribute to the spin polarization on the outermost surface. The thicknesses of the metallic films (10 and 25 nm) are close to the spin diffusion lengths of the electron in these transition metals. A potential gradient also exists at the metal/substrate interface due to the difference of the metal and the substrate. In consideration of the Rashba effect at the metal/substrate interface, the transverse spin polarization calculated from Eq. (3) will increase and be more consistent with the experimental result from spin-polarized positron beam. To check this assumption in a future research, a metal/substrate interface with a strong Rashba effect is needed for the experiment.
It is known that Pt and Pd nano-structures nearly satisfy the Stoner criterion and hence ferromagnetic behavior appears37,38. This implies that ferromagnetic order will easily be induced in Pt and Pd surfaces. A recent anomalous Hall effect study of a  sample suggests that a magnetic moment of ~10 µB is induced by an applied electric field39. The Rashba field induced by the charge current may also contributes to the development of ferromagnetic order on the surface.
sample suggests that a magnetic moment of ~10 µB is induced by an applied electric field39. The Rashba field induced by the charge current may also contributes to the development of ferromagnetic order on the surface.
To summarize, we have observed huge CISP on the outermost surfaces of Pt, Pd, Ta and W thin films by using a spin-polarized positron beam. The sign and magnitude of the CISP on these metal surfaces are explained by the Rashba-Edelstein mechanism. This work demonstrates that the spin-polarized positron beam is a useful technique for observing the outermost surface spin polarization of spintronics materials.
Methods
Figure 5(a) shows the principle of Ps formation and annihilation. Spin-polarized positrons implanted into the sub-surface region are emitted into vacuum as Ps. Two types of Ps exist: spin-triplet ortho-Ps (|S, m〉 = |1, 0〉, |1, 1〉, |1, −1〉) and spin-singlet para-Ps (|S, m〉 = |0, 0〉), where S and m are the total spin and the magnetic quantum number, respectively. Ortho-Ps decays into three γ rays, giving rise to a continuous energy distribution from 0 to 511 keV. Para-Ps decays into two γ rays of ~ 511 keV, that overlaps with direct annihilation of positrons with electrons inside the sample. In the deep region of the metal, the probability of Ps formation is negligible. Shown as the shaded area in Fig. 5(b), the 3γ annihilation of ortho-Ps (below 511 keV peak) near the surface is clearly observable.
(a) Principle of Ps formation and annihilation. Positrons (e+) implanted into the subsurface region are emitted into vacuum as Ps by picking up electrons (e−) from the outermost surface. When the polarizations of positrons and electrons are parallel (anti-parallel), more (less) ortho-Ps (S = 1) is formed. (b) Typical energy spectra of annihilation γ rays obtained at positron energies of E+ = 12 keV and 50 eV. The total intensity is normalized to the 511 keV area intensity. The increment ΔR represents the 3γ annihilation of ortho-Ps.
The fraction of each spin state of Ps is given by13:




where P+ and P− are spin polarizations of the positrons and the electrons, respectively and ϕ is the relative angle of P− to P+. The formation probability of para-Ps is  and that of ortho-Ps is
and that of ortho-Ps is

where  and
and  are detection efficiencies of annihilation γ rays from |1, 1〉 plus |1, −1〉 and |1, 0〉, respectively. The values of
are detection efficiencies of annihilation γ rays from |1, 1〉 plus |1, −1〉 and |1, 0〉, respectively. The values of  and
and  depend on the angle between the γ ray detector and P+.
depend on the angle between the γ ray detector and P+.
The intensity of the annihilation energy spectrum below 511 keV is a function of  40:
40:

where T is the total area under the intensity curve, U is the area under the 511 keV peak and the subscripts 0 and 1 of R and U denote 0% and 100% Ps emission, respectively. For small  ,
,  . Thus, the asymmetry of ΔR upon spin flip (+P− ↔ −P−) can be written as12
. Thus, the asymmetry of ΔR upon spin flip (+P− ↔ −P−) can be written as12

From the known values of P+,  and the experimental asymmetry, the transverse spin polarization (P−cosϕ) is determined. For the detector alignment in the present study (perpendicular to the positron beam), the factor
and the experimental asymmetry, the transverse spin polarization (P−cosϕ) is determined. For the detector alignment in the present study (perpendicular to the positron beam), the factor  in Eq. (10) is 0.6.
in Eq. (10) is 0.6.
References
Maekawa, S., Valenzuela, S. O., Saitoh, E. & Kimura, T. Spin Current (Oxford University Press, Oxford, England, 2012).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: Inverse spin Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Ando, K. & Saitoh, E. Inverse spin Hall effect in palladium at room temperature. J. Appl. Phys. 108, 113925 (2010).
Liu, L. Q. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Pai, C. F. et al. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101, 122404 (2012).
Bychkov, Y. A. & Rashba, E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C 17, 6039–6045 (1984).
Varykhalov, A. et al. Ir(111) surface state with giant Rashba splitting persists under graphene in air. Phys. Rev. Lett. 108, 066804 (2012).
Ast, C. R. et al. Giant spin splitting through surface alloying. Phys. Rev. Lett. 98, 186807 (2007).
Ast, C. R. et al. Local detection of spin-orbit splitting by scanning tunneling spectroscopy. Phys. Rev. B 75, 201401(R) (2007).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004).
Mills, A. P., Jr Positronium formation at surfaces. Phys. Rev. Lett. 41, 1828–1831 (1978).
Gidley, D. W., Köymen, A. R. & Capehart, T. W. Polarized low-energy positrons: A new probe of surface magnetism. Phys. Rev. Lett. 49, 1779–1783 (1982).
Kawasuso, A. et al. Current-induced spin polarization on a Pt surface: A new approach using spin-poalrized positron annihilation spectroscopy. J. Magn. Magn. Mater. 342, 139–143 (2013).
Kawasuso, A. & Maekawa, M. Spin-polarization of an electro-static positron beam. Appl. Surf. Sci. 255, 108–110 (2008).
Jiang, A. et al. The structure and stability of β-Ta thin films. Thin solid films 479, 166–173 (2005).
Weerasekera, I. A., Shah, S. I., Baxter, D. V. & Unruh, K. M. Structure and stability of sputter deposited beta-tungsten thin films. Appl. Phys. Lett. 64, 3231–3233 (1994).
Karabacak, T., Wang, P. I., Wang, G. C. & Lu, T. M. Phase transformation of single crystal β-tungsten nanorods at elevated temperatures. Thin solid films 493, 293–296 (2005).
Coleman, P. Positron Beams and their Applications (World Scientific, Singapore, 2000).
Chu, S., Mills, A. P. Jr. & Murray, C. A. Thermodynamics of positronium thermal desorption from surfaces. Phys. Rev. B 23, 2060–2064 (1981).
Rosenberg, I. J., Howell, R. H. & Fluss, M. J. Temperature dependence of the positronium work function. Phys. Rev. B 35, 2083–2086 (1987).
Michaelson, H. B. The work function of the elements and its periodicity. J. Appl. Phys. 48, 4729–4733 (1977).
Kimura, T., Otani, Y., Sato, T., Takahashi, S. & Maekawa, S. Room-temperature reversible spin Hall effect. Phys. Rev. Lett. 98, 156601 (2007).
Ando, K. et al. Electric manipulation of spin relaxation using the spin Hall effect. Phys. Rev. Lett. 101, 036601 (2008).
Mosendz, O. et al. Detection and quantification of inverse spin Hall effect from spin pumping in permalloy/normal metal bilayers. Phys. Rev. B 82, 214403 (2010).
Liu, L. Q., Moriyama, T., Ralph, D. C. & Buhrman, R. A. Spin-torque ferromagnetic resonance induced by the spin Hall effect. Phys. Rev. Lett. 106, 036601 (2011).
Morota, M. et al. Indication of intrinsic spin Hall effect in 4d and 5d transition metals. Phys. Rev. B 83, 174405 (2011).
Kondou, K., Sukegawa, H., Mitani, S., Tsukagoshi, K. & Kaisai, S. Evaluation of spin Hall angle and spin diffusion length by using spin current-induced ferromagnetic resonance. Appl. Phys. Exp. 5, 073002 (2012).
Hahn, C. et al. Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta. Phys. Rev. B 87, 174417 (2013).
Althammer, M. et al. Quantitative study of the spin Hall magnetoresistance in ferromagnetic insulator/normal metal hybrids. Phys. Rev. B 87, 224401 (2013).
Tanaka, T. et al. Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals. Phys. Rev. B 77, 165117 (2008).
Kontani, H., Tanaka, T., Hirashima, D. S., Yamada, K. & Inoue, J. Giant orbital Hall effect in transition metals: Origin of large spin and anomalous Hall effects. Phys. Rev. Lett. 102, 016601 (2009).
Zhang, S. F. Spin effect in the presence of spin diffusion. Phys. Rev. Lett. 85, 393–396 (2000).
Edelstein, V. M. Spin polarizaton of conduction electrons induced by electric current in twodimensional asymmetric electron systems. Sol. Stat. Commun. 73, 233–235 (1990).
Gambardella, P. & Miron, I. M. Current-induced spin-orbit torques. Philos. Trans. A Math. Phys. Eng. Sci. 369, 3175–3197 (2011).
Rojas Sánchez, J. C. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. commun. 4, 2944 (2013).
Schwab, P., Raimondi, R. & Gorini, C. Inverse spin Hall effect and anomalous Hall effect in a two-dimensional electron gas. EPL 90, 67004 (2010).
Liu, X. et al. Structure and magnetization of small monodisperse platinum clusters. Phys. Rev. Lett. 97, 253401 (2006).
Sampedro, B. et al. Ferromagnetism in fcc twinned 2.4 nm size Pd nanoparticles. Phys. Rev. Lett. 91, 237203 (2003).
Shimizu, S. et al. Eletrically tunable anomalous Hall effect in Pt thin films. Phys. Rev. Lett. 111, 216803 (2013).
Lynn, K. G. & Welch, D. O. Slow positrons in metal single crystals. I. Positronium formation at Ag(100), Ag(111) and Cu(111) surfaces. Phys. Rev. B 22, 99–110 (1980).
Acknowledgements
We are grateful to B. Gu, J. Ieda and S. Maekawa of Japan Atomic Energy Agency (JAEA) for their valuable suggestions and discussions. This work was financially supported by JSPS KAKENHI Grant No. 24310072 and a Grant for Basic Science Research Projects from the Sumitomo Foundation.
Author information
Authors and Affiliations
Contributions
A.K. constructed the spin-polarized positron beam, A.K., Y.F., M.M. and H.J.Z. constructed the CISP measurement system. H.J.Z. proposed the project. E.S., K.T., T.S., H.J.Z. and S.Y. prepared the samples, H.J.Z. and H.L. performed the CISP experiments, S.Y. performed the XRD experiments. H.J.Z. performed the data analysis and wrote the manuscript, all authors discussed the results and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Zhang, H., Yamamoto, S., Fukaya, Y. et al. Current-induced spin polarization on metal surfaces probed by spin-polarized positron beam. Sci Rep 4, 4844 (2014). https://doi.org/10.1038/srep04844
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04844
This article is cited by
-
Observation of current-induced bulk magnetization in elemental tellurium
Nature Communications (2017)
-
Multi-Terminal Spin Valve on Channels with Spin-Momentum Locking
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.