Introduction

Spirals, also known as rotors1 or vortices2, occur in various excitable systems, including chemical media3,4,5, aggregations of Dictyostelium discoideum amoebae6 and cardiac tissues7. In hearts, spirals and subsequent turbulences may cause lethal arrhythmia8,9,10,11,12. Better than traditional therapies13, a new approach using wave emission from heterogeneities (WEH) or far-field stimulation provides a promising alternative to terminate arrhythmia14,15,16,17. This approach is based on the fact that, by the application of an external electric field to a whole piece of tissue, de-polarizations and hyper-polarizations (so-called Weidmann zones18) could be induced near obstacles (conductivity heterogeneities). These obstacles correspond to blood vessels, ischemic regions and smaller-scale discontinuities. If the electric strength exceeds some threshold, obstacles can act as virtual electrodes or second sources19,20,21,22,23,24,25.

The life-saving motivation to terminate arrhythmia has sparked many discussions about the mechanism of WEH26,27,28,29,30,31,32. However, previous works focus on WEH in response to the uniform electric field (UEF), which is realized by applying DC pulses onto field electrodes14,15,16,17. Recently, the circularly polarized electric field (CPEF) has shown its unique ability to control spirals and turbulences33,34 and has been verified in the Belousov-Zhabotinsky reaction by applying two ACs onto two pairs of field electrodes perpendicular to each other35.

In this paper, we study the mechanism of WEH induced by CPEF and find that its ability to unpin anchored spirals, which is an important step in terminating arrhythmia, has advantages over UEF, such as lower voltage, higher success rate and larger application scope. Therefore, as a lower-voltage higher-efficiency approach, CPEF is more applicable in terminating arrhythmia.

In the following, without loss of generality, we use a counter-clockwise rotating CPEF to unpin anchored spirals, which can be expressed as E = (Ex, Ey), where Ex = E0 cos(ωet + ϕe), Ey = E0 cos(ωet + ϕe + 3π/2) and E0, ωe, ϕe are its strength, angular frequency and initial phase relative to x axis. In mono-domain models, the general effect of an external electric field on an obstacle can be expressed as an additional no-flux boundary condition26,29: n ·∇(V + E·r) = 0, where n is the normal vector to the obstacle boundary, V is the membrane potential, E is the external electric field and r is a point on the boundary. Therefore, in the presence of a circular obstacle (radius R) influenced by CPEF, the boundary condition can be described in the polar coordinate (ρ, θ) as

Our numerical analysis is based on the evolution equations, which describe the membrane potential V across the cellular membrane, along with a number of gating variables, collectively denoted as y, characterizing the conductance of various ionic channels. Symbolically, the system can be expressed as

where functions Iion and F are determined by different ionic currents in different models, C is the membrane capacitance and D is the diffusion current coefficient. To demonstrate the results found in this paper are robust and essentially independent of precise ionic currents, we use both Luo-Rudy model36 and Barkley model37.

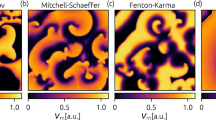
Based on equation (1), to describe the distribution of the membrane potential induced by CPEF near a circular obstacle, we apply CPEF at a weak strength in a two-dimensional quiescent medium. As shown in Fig. 1a (Luo-Rudy model) and 1c (Barkley model), the mechanism of WEH in response to CPEF rests on the induced de-polarization (red region) and hyper-polarization (blue region) near the obstacle. In both Luo-Rudy model and Barkley model, comparing to the dipole-like patterns induced by UEF28,14,15,16,17 (Fig. 1b and 1d), the patterns induced by CPEF have two novel characters: one is that, they rotate synchronously with the rotating CPEF; the other is that, their patterns are similar as Chinese “ancient Taijitu”. Depending on attaching to the obstacle or not, we divide both de-polarization and hyper-polarization into “Head” and “Tail” (Fig. 1a).

Figure 1
figure 1

Distribution of the membrane potential induced by CPEF and UEF.

(a), CPEF in Luo-Rudy model, E0 = 0.05 V/cm, ωe = 0.2 rad/ms. (b), UEF in Luo-Rudy model, E0 = 0.05 V/cm. (c), CPEF in Barkley model, E0 = 0.05, ωe = 4. (d), UEF in Barkley model, E0 = 0.05. In this and following numerical simulations of Luo-Rudy model, the obstacle size R = 0.32 cm and the excitability is set as same as in Ref. 38. In this and following numerical simulations of Barkley model, the obstacle size R = 3 and unless otherwise specified, the excitability is set as a = 0.8, b = 0.06. The obstacles are all applied additional no-flux boundary conditions as equation (1) shows. The red dotted arrows represent the directions of electric field. The red curved arrows mean CPEFs rotate counter-clockwise. The red and blue regions around obstacles demonstrate de-polarizations and hyper-polarizations, respectively. The two black double-headed arrows indicate how we divide the “Head” and “Tail”. The patterns in (b) and (d) which we get from simulations are the same as in Fig. 1a of Ref. 28.

Full size image

The stably-rotating and fantastically-shaped de-polarization and hyper-polarization elucidated above can be used to unpin anchored spirals if the CPEF's strength E0 exceeds a certain value and angular frequency ωe is tuned to a proper value. In cardiac tissues, anchored spirals may have clockwise or counter-clockwise rotating directions. Therefore, to get a more comprehensive understanding about unpinning by CPEF, we discuss these two types of rotating directions separately.

Firstly, we numerically simulate a clockwise rotating anchored spiral at the angular frequency ωs and discuss its unpinning mechanism by CPEF. In Luo-Rudy model as shown in Fig. 2a, at t = 0, ϕe is the initial phase of CPEF relative to x axis, ϕs is the initial phase of the anchored spiral front relative to x axis. In cardiac tissues, ϕe is always given at a certain value, while ϕs would be arbitrary. But in order to keep wave patterns simple and get a convenient structure analysis by numerical simulations, we choose ϕe is arbitrary but restrict ϕs to zero. Furthermore, we can define the initial phase difference between ϕe and ϕs as Δϕ = ϕe − ϕs, to simply demonstrate the initial configuration of CPEF and the anchored spiral. Hence, the configuration at t = 0 in Fig. 2a can be defined as a given Δϕ. Then at t = 20 ms, a new wave N has been nucleated and begins to collide and merge with the anchored spiral S. Later at t = 40 ms, the colliding parts have detached from the obstacle and form a new free spiral S′. Although there is another new wave N′ nucleated by CPEF, its evolvement does not affect the final result. So after applying CPEF for a period in which an anchored spiral rotates one round (2π/ωs), there will be only S′ left. And after ceasing CPEF for another period of 2π/ωs, at t = 105 ms, S′ does not re-pin to the obstacle but still keeps rotating freely. This is viewed as a “successful unpinning”30.

Figure 2
figure 2

Unpinning the clockwise rotating anchored spiral by CPEF.

(a), In Luo-Rudy model, the angular frequency of spiral ωs = 0.136 rad/ms. The CPEF's strength E0 = 0.7 V/cm and angular frequency ωe = 0.1 rad/ms. CPEF is applied from t = 0 to t = 46.2 ms. ϕe is the initial phase of CPEF relative to x axis and ϕs is the initial phase of the anchored spiral front relative to x axis and set as zero. (b), In Barkley model, the angular frequency of spiral ωs = 1.024. The CPEF's strength E0 = 1.8 and angular frequency ωe = 3.686. CPEF is applied from t = 0 to t = 6. N and N' represent different new waves nucleated by CPEF in different time. S and S' represent the initial anchord spiral and the new free spiral, respectively. White arrows are the propagation directions of waves.

Full size image

Additionally, the unpinning procedure above is much clearer in Barkley model, as shown in Fig. 2b. At the start, the configuration of CPEF and the anchored spiral S is introduced by a given Δϕ. Then, at t = 1.0 when the phase of CPEF is 1.0ωe + ϕe, a new wave N has been nucleated by the de-polarization. The one end of N, corresponding to the “Head” of de-polarization, is going to collide with S. Later at t = 1.8, the colliding parts merge with each other. And the other end of N, corresponding to the “Tail” of de-polarization, has detached from the obstacle, because its propagation along the boundary of obstacle is inhibited by both the “Head” of hyper-polarization and the refractory tail of S. Thereby, N and S form a new unpinned spiral S′. Because of the continuing CPEF, another new wave N′ has been nucleated by CPEF, but N′ has no effect to the final result. Finally, S′ can be viewed as a successfully unpinned spiral. Therefore, we can recognize such Δϕ can lead to successful unpinning and call it the proper Δϕ.

In the next, we discuss the other mechanism about unpinning a counter-clockwise rotating anchored spiral by CPEF with a proper Δϕ. In Luo-Rudy model (Fig. 3a), at the start of applying CPEF (t = 0), an anchored spiral S is counter-clockwise rotating around the obstacle. Then at t = 8 ms, a new wave N is nucleated by CPEF. Later at t = 25 ms, S is unpinned from the obstacle. Finally, at t = 105 ms, S rotates freely, which satisfy the requisite of successful unpinning.

Figure 3
figure 3

Unpinning the counter-clockwise rotating anchored spiral by CPEF.

(a), In Luo-Rudy model, the angular frequency of spiral ωs = 0.136 rad/ms. The CPEF's strength E0 = 0.7 V/cm and angular frequency ωe = 0.1 rad/ms. CPEF is applied from t = 0 to t = 46.2 ms. (b), In Barkley model, the angular frequency of spiral ωs = 1.024. The CPEF's strength E0 = 1.8 and angular frequency ωe = 3.686. CPEF is applied from t = 0 to t = 6.

Full size image

The clearer process can be seen in Barkley model (Fig. 3b). Similarly at the start, the configuration of CPEF and the anchored spiral is introduced by a proper Δϕ. Then at t = 2.0, a new wave N is nucleated due to the de-polarization induced by CPEF. Later at t = 2.4, the anchored spiral S gradually falls into the “Head” of hyper-polarization induced by CPEF, which is at the opposite obstacle boundary of N. Because of the inhibition caused by the “Head” of hyper-polarization, S is unpinned. Furthermore, because of the inhibition caused by the “Tail” of hyper-polarization, S is driven further away from the obstacle. Although N is still rotating along the obstacle, it makes no effect to the final result and S will evolve to a successfully unpinned spiral.

To summarize, we get two types of unpinning mechanisms by CPEF: for a given CPEF and excitability, with the proper Δϕ, the rotating de-polarization and hyper-polarization induced by CPEF can lead to successful unpinning, corresponding to Figs. 2 and 3 respectively.

Therefore, we can consider Δϕ is an important factor for successful unpinning. We define the whole range of Δϕ which can lead to successful unpinning as the unpinning window {Δϕ}unpin. Since Δϕ is in the interval of [0, 2π), {Δϕ}unpin can be normalized by 2π as

ρuw also means the success rate of an arbitrary Δϕ whether or not can lead to successful unpinning under the given CPEF and excitability.

With given excitability which determines ωs of an anchored spiral, ρuw is highly related to the angular frequency ωe and strength E0 of CPEF. Among a certain range of ωe, ρuw can be optimized to its maximum. So we define the ωe giving maximal ρuw as the optimal ωe. Although different excitabilities (corresponding to different ωs) have different optimal ωe to optimize ρuw, the ratio of optimal ωe over given ωs keeps basically invariant. Thus we define this ratio as the optimal ωe/ωs. We illustrate this relation between ρuw and the optimal ωe/ωs, in the case of unpinning the counter-clockwise rotating anchored spiral in Barkley model under a certain excitability and electric strength, as red dotted line in Fig. 4. Beside optimal ωe/ωs, a proper electric strength E0 can also optimize ρuw. As also shown in Fig. 4, larger E0 makes larger ρuw. And there is a limit beyond which increasing E0 makes no contribution to enhance ρuw any more. On the other hand, a high electric strength harms hearts. So this limit value (e. g. E0 = 1.8 in Barkley model, as illustrated by black solid line in Fig. 4) could be used as the optimal electric strength.

Figure 4
figure 4

The relations between ρuw and ωe/ωs in Barkley model.

Different lines represent ρuw plotted against ωe/ωs under different E0. We choose interval [3.0, 4.0] for instance to reflect the existence of the optimal ωe/ωs. Since the range centered around ωe/ωs = 3.6 has a relative large ρuw even under a weak electric strength (e.g. E0 = 0.8, red dotted line), we adopt this ratio as the optimal ωe/ωs in following numerical simulations of Barkley model.

Full size image

Now with the optimal settings of CPEF (E0, ωe), we can examine the ability of CPEF to unpin anchored spirals in various excitabilities and compare it to the results by UEF. Firstly, to know how high the success rate (value of ρuw) is in various excitabilities, we take a part of excitability region (a = 0.8, b = 0~0.14) for instance, as Fig. 5 shows. In this excitability region, ρuw of CPEF reaches to an average of 80%, which is much higher than ρuw of UEF31. It is clear that CPEF is very effective in successfully unpinning both counter-clockwise (blue solid line) and clockwise (red dashed line) rotating anchored spirals. Especially in weak excitabilities (b > 0.11), ρuw of UEF is less than 40%, but ρuw of CPEF reaches 100%. This means that, regardless of Δϕ, CPEF can always successfully unpin anchored spirals in weak excitabilities. Moreover, in high excitabilities (b<0.06), UEF is failed at successfully unpinning any anchored spirals, but CPEF is still capable of successfully unpinning at an appreciable success rate (ρuw > 40%). In addition, the optimal strength of CPEF (E0 = 1.8) required for successful unpinning is much smaller than the optimal strength of UEF (E0 = 7 in Ref. 31).

Figure 5
figure 5

A comparison of the success rate (value of ρuw) of CPEF and UEF in various excitabilities in Barkley model.

The excitability is varied by changing b from 0 to 0.14 but fixing a to be 0.8. The blue solid and red dashed lines represent the success rate of unpinning counter-clockwise and clockwise spirals by CPEF respectively, at E0 = 1.8, ωe = 3.6ωs. The black dotted line describes the success rate by UEF with the optimal strength E0 = 7, which we get from simulations and is the same as in Fig. 5a of Ref. 31.

Full size image

Beside of high success rate, in the parameter space about excitability, the application scope of CPEF, i.e. the extent where ρuw > 0, takes effect through the whole region where the medium exhibits excitable dynamics and supports spirals and is much larger than the application scope of UEF31. This is illustrated in Fig. 6: The area representing the application scope of CPEF (gray region) fulfills the whole region where spirals sustain (SW region), but the area representing the application scope of UEF (shaded region) is just within a part of SW region. Since cardiac tissues may distribute across SW region, CPEF is more applicable than UEF to unpin anchored spirals.

Figure 6
figure 6

A comparison of the application scope of CPEF and UEF in Barkley model.

Three solid lines separate the whole parameter space about excitability into four regions marked by red double-headed arrows. In SW region, the medium exhibits excitable dynamics and supports spirals. For others, NW, RW and BI regions represent no wave, retracting waves and bi-stability, respectively. The shaded region represents successful unpinning by UEF with the optimal strength E0 = 7, which we get from simulations and is the same as in Fig. 2b of Ref. 31. The gray region including the shaded region represents successful unpinning by CPEF (E0 = 1.8, ωe = 3.6ωs). The vertical dotted line is corresponding to the chosen excitability used in Fig. 5.

Full size image

In summary, we study the unique mechanism of WEH induced by CPEF and find its outstanding ability to successfully unpin anchored spirals is better than UEF, at the higher success rate and larger application scope, even with a lower voltage. This is due to the unique characteristics of WEH induced by CPEF: in contrast to the dipole-like pattern induced by UEF28,14,15,16,17, the pattern induced by CPEF is ancient-Taijitu-like (i.e. each of de-polarization and hyper-polarization has “Head” and “Tail”) and rotates synchronously with the rotating CPEF. Therefore, in the case of unpinning by de-polarization, UEF would fail if the de-polarization is within the refractoriness of the anchored spiral and therefore cannot nucleate a new wave to unpin it. However, the rotating de-polarization induced by CPEF would escape from the refractoriness over time and nucleate a new wave easily. And the “Tail” of de-polarization induced by CPEF can form an unpinned new spiral's tip naturally, since it is originally unpinned. In the case of unpinning by hyper-polarization, UEF would fail if the hyper-polarization is not within the attached region of the anchored spiral and therefore cannot unpin it. However, the rotating hyper-polarization induced by CPEF would meet the attached region of the anchored spiral over time and unpin it easily. Moreover, the “Tail” of hyper-polarization induced by CPEF can drive the unpinned spiral further away from the obstacle, to prevent re-pinning which is an important cause to unsuccessful unpinning by UEF.

We believe, the outstanding ability of WEH induced by CPEF to unpin anchored spirals can be easily verified in cardiac tissues: instead of applying two DCs onto two pairs of field electrodes perpendicular to each other to deliver UEF in the experimental preparation of Fig. 5D in Ref. 16, one can apply two ACs onto these two pairs of field electrodes to realize CPEF in cardiac tissues, which is similar with the case in the Belousov-Zhabotinsky reaction of Ref. 35. We hope this lower-voltage higher-effectiveness approach may provide a better alternative to traditional therapies in terminating arrhythmia.

Methods

The Luo-Rudy model36 can be expressed as

where V is the membrane potential and Iion is the total ionic currents which consist of a fast sodium current INa, a slow inward current Isi, a time-dependent potassium current IK, a time-independent potassium current IK1, a plateau potassium current IKp and a time-independent background current Ib. Cm = 1 μF/cm2 is the membrane capacitance and D = 0.001 cm2/ms is the diffusion current coefficient.

In the polar coordinate, equation (4) is integrated on a Nρ × Mθ = 75 × 336 uniform grid with no-flux boundary conditions via Euler method and a five-point finite difference scheme is applied to compute the Laplacian term ∇2V. The space and time step are Δρ = 0.02 cm, Δθ = π/168 and Δt = 0.001 ms.

The Barkley model37 can be expressed as

where u is the fast variable corresponding to the membrane potential and v is a slow variable corresponding to the recovery process. The parameter ε determines the timescale of u which is fixed to 0.02. And the parameters a and b control the excitability of the medium: Larger a increases the action potential duration and larger b/a increases the excitation threshold.

In the polar coordinate, equation (5) is integrated on a Nρ ×Mθ = 91 × 396 uniform grid with no-flux boundary conditions via Euler method and a five-point finite difference scheme is applied to compute the Laplacian term ∇2u. The space and time step are Δρ = 1/6, Δθ = π/198 and Δt = 2 × 10−4.