Abstract
We have carried out a comparative analysis of data collected in three experiments on Prisoner's Dilemmas on lattices available in the literature. We focus on the different ways in which the behavior of human subjects can be interpreted, in order to empirically narrow down the possibilities for behavioral rules. Among the proposed update dynamics, we find that the experiments do not provide significant evidence for non-innovative game dynamics such as imitate-the-best or pairwise comparison rules, whereas moody conditional cooperation is supported by the data from all three experiments. This conclusion questions the applicability of many theoretical models that have been proposed to understand human behavior in spatial Prisoner's Dilemmas. A rule compatible with all our experiments, moody conditional cooperation, suggests that there is no detectable influence of interaction networks on the emergence of cooperation in behavioral experiments.
Similar content being viewed by others
Introduction
Cooperation is a key ingredient to understand evolution and, in particular, the major transitions that took place since the Earth formed1. It is also fundamental for animal and human societies to arise and thrive2. Notwithstanding its importance, how cooperation can survive the threat of free-riders, i.e., individuals that reap the benefits of others' help without providing anything for the common good, is still a very active area of research. This poses a conundrum that was already noticed almost a century and half ago by Darwin3. A theoretical framework that has been widely used in the past to shed light on these issues is the Prisoner's Dilemma (PD)4,5. In the two-player PD, when both of them cooperate, they obtain the maximum joint benefit; however, free-riding when meeting a cooperator leads to the highest individual payoff, thus leading to a dilemma as mutual defection is worse than mutual cooperation. In this context, for cooperators to outcompete defectors, there must be something that favors the former and help them take over the population. Generally speaking, this can be accomplished through assortment6, i.e., by having cooperators interact mostly or only with other cooperators; alternatively, punishment7,8 has also been shown to significantly promote cooperation.
In the last five decades, several mechanisms, processes or interaction structures have been proposed leading to the survival of cooperators (see, e.g., Refs. 9, 10 for reviews). In 1964 Hamilton11,12 suggested that kin selection, namely the fact that individuals cooperate only with others that are genetically related to them led to the emergence and stability of cooperation. Subsequently, Trivers13 and Axelrod and Hamilton14 introduced reciprocity, that consists of cooperating with those that cooperated with you in the past. When this reciprocity is indirect, Alexander15 and Nowak and Sigmund16,17 showed that it can also promote the appearance of cooperation. Yet another mechanism helping cooperators vs defectors is group (or multilevel) selection3,18,19, a somewhat controversial proposal that has been subjected to a lot of discussion. Last, but not least, Axelrod5 suggested and Nowak and May20 showed by means of numerical simulations, that when the players were placed on a lattice, if cooperators were together in clusters they could outcompete defectors, a mechanism that has been termed spatial reciprocity (or network reciprocity when the population structure is not a planar graph).
In particular, spatial reciprocity has received a lot of attention from theorists. Many models have explored analytically and by simulation the effects of a network structure on the promotion of cooperation, mostly in the framework of the PD (or the Public Goods game, as almost always the action played must be the same for all partners), but the results of these models largely depend on details such as the type of spatial structure or the evolutionary dynamics (see, e.g., Refs. 21, 22 for reviews). On the experimental side, to our knowledge, there are only a few experiments of this kind based on human subjects23: on small random, small world and local networks24, on rings25, on small regular lattices26; on medium size regular lattices27; on small networks of different kinds; and, finally, a recent experiment by28 on a large lattice and a large heterogeneous (fat-tailed) network. Although the setup of all experiments is fairly similar, their details are rather different and the effect of those details on the results is not totally clear, but might be of crucial importance for the development of further theories. Therefore, further analysis of the data available so far are needed in order to reach definite conclusions. To contribute to this goal, here we present a comparative analysis of three of these experiments in order to extract the properties underlying all of them and that can be considered independent of the details of the setups in order to give as much generality and support as possible to our conclusions.
Available experiments: setups and data
We focus on the three experiments on regular lattices: one performed in Plön25 (in fact, although we refer to the experiment by the name “Plön” after the group that organized it, sessions were conducted in Kiel, Cologne and Bonn), another one in Madrid26 and finally a last one in Zaragoza28. In these experiments the participants were virtually located on the nodes of a square lattice with periodic boundary conditions (topologically, on a torus). They played a PD game in the same way as in most theoretical models, with each of their neighbors choosing only one action, the same for all of them. The payoffs were calculated by adding the payoffs of individual games with each neighbor. After each round, players were informed about their action and payoff, as well as the actions and payoffs of their neighbors. Based on this information and their experience from previous interactions, they had to decide on their next action.
It is important to stress that all three experiments were carried out with real human subjects, invited to participate in person (and not only online) as volunteers among last-year high school or undergraduate students. This is the reason why for the largest studies there were logistic problems that made it difficult to have independent control groups. Indeed, the experiments had two types of treatments: one in which the network was the same for all rounds of the game and another one, where the network was shuffled after every round, as control. However, in Madrid and Zaragoza the experiment and control treatment were performed subsequently; hence, players already had experience in the control treatment. On the contrary, in Plön, the control treatment was performed with new groups of players without previous experience. This makes the comparison of the control treatments very difficult and therefore in this paper we will focus only on the experimental treatments. On the other hand, having large system sizes is important to bring the experimental studies closer to the theoretical research as we will see shortly.
References 25, 26, 28 give a full description of their respective experimental setups, including in some cases the instructions that were given to the participants. Here, for the sake of completeness, we summarize the main features of the experiments and we refer the reader to the original publications for full details. In Plön, the experiment was performed on a 4 × 4 square lattice where players interacted with four neighbors in their von Neuman neighborhood. The experiment treatment was carried out in 15 independent sessions, whereas the control treatment (performed with independent groups of players as stated above) was repeated 10 times, each with 16 players playing 25 rounds. Players could only take part in one session. In Madrid, the experiment was performed on an order of magnitude larger lattice, of size 13 × 13 (a single group of 169 subjects in total) and volunteers played with the eight neighbors from their Moore neighborhood. As was mentioned above, the size of the experiment made it difficult to get an independent group of players for the control treatment and it was performed with the same subjects who previously played the experiment treatment; these large experiments have serious logistic problems and running them twice would be an enormous effort (and cost). Therefore, they had a control treatment as described and subsequently they went through another game of the experiment treatment again, with a different set of neighbors. The largest experiment was performed in Zaragoza. It tested two different types of networks: a 25 × 25 regular lattice with degree k = 4 and periodic boundary conditions (625 subjects) and a heterogeneous network with a fat-tailed degree distribution (604 subjects, the number of neighbors varied between k = 2 and k = 16). The treatments were analogous to those of the Madrid experiment and also performed in sequence: first the experimental treatment and subsequently the control treatment with the same players. No repetition of the experiment treatment was carried out in this case.
Aside from the differences in the control treatments, the experiments themselves had also differences of their own, which are more relevant to their comparison. Table 1 summarizes these differences. To begin with, as we have mentioned above, the size of the virtual networks ranges from the smallest one (4 × 4) in Plön's experiment to the largest one (25 × 25) of Zaragoza's experiment. The size of the network could have a significant influence on the promotion of cooperation, because the formation of clusters of cooperators (which is the known mechanism by which cooperation can be promoted) only has a chance if the networks are large enough. Furthermore, the local structure of the networks is different. In Plön and Zaragoza, players had four nearest neighbors; in Madrid they played with the eight surrounding neighbors. Notice that this introduces a crucial difference in the local structure of the network, because the clustering coefficient of the lattice with four neighbors is zero, whereas that of the network with 8 neighbors is 3/7. Since the clustering can significantly influence the promotion of cooperation22, this difference might be important.
Beyond sizes and number of neighbors, another important difference is the payoff matrix. In Plön, players played a strict PD where the punishment for mutual defection, P, is larger than the sucker's payoff (the payoff for a cooperator facing a defector, S); in Madrid and Zaragoza, the game played was a weak PD, where P = S = 0, which is more favorable to cooperation: namely, in the weak PD, cooperating in a situation where everybody is defecting is not costly, whereas in the strict PD, players earn more by defecting against defectors and therefore it is to be expected that they cooperate less (or, as put in29, there is greed in the game, but not fear). Moreover, the framing of the experiment was not the same: In Madrid and Zaragoza, the language describing the experiment to the participants in the instructions was completely neutral and actions were represented by colors, whereas in Plön actions were referred to as cooperative or non-cooperative. Instructions are available as supplementary material to each publication and in any case from the authors upon request. Finally, in Plön, 15 independent sessions were performed, whereas in the Madrid and Zaragoza experiments, because of the size of the networks, this was not possible. However this should not influence the results much, since the individual perspective is the same in all cases. The number of actions in each round is of the same order of magnitude for all experiments: 240 actions per round (the Plön experiment), 169 actions per round (Madrid experiment) and 625 actions per round (Zaragoza experiment).
Global observables
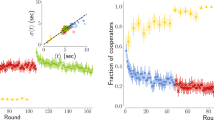
Let us start the analysis with the global cooperation level. Figure 1 (top left) shows the fraction of cooperative players in each round of the experiments. We see that in all three experiments cooperation starts at rather high levels (between 55% and 70%) and subsequently declines rapidly and settles on a small but non zero level (between 15% and 35%). In the Plön experiment the initial cooperation level was the largest one, but the decline was the fastest and the final level was the smallest. Larger initial fractions of cooperative actions in this case may also arise from the more positive framing of the instructions discussed above. Although there are small differences in the levels of cooperation, each of them is significantly lower than the one predicted by the theoretical models20,21,22. A question may also arise as to whether our experiments have reached an asymptotic, stationary state. While this may not be the case, the theoretical models make assumptions on the players' behavior that allow also an analysis of the non-stationary state, as we will see below.
Main experimental results.
(Top left) Fraction of players who cooperated in each round. (Top right) Fraction of players who cooperated a given fraction of the rounds. (Bottom left) Fraction of players who earned a given amount, normalized by the average earning of all players in the same experiment. (Bottom right) Scatter-plot of earnings vs cooperativeness of the players. Each point represents one player, described by the fraction of rounds in which the player cooperates and the player's earnings normalized by the average earning of all the players. Slopes of the fits are following: Plön experiment s = −0.61, Madrid experiment s = −0.64 and Zaragoza experiment s = −0.50 (p < 0.001 in all cases).
In Figure 1 (top right) we show the distribution of players by their fractions of cooperative actions during the game. Two differences are noticeable. First, in Madrid we have a high number of pure defectors, which are missing in the other two experiments. The exact mechanism leading a sizeable number of players to become defectors is unclear. In this respect, it is worth recalling another recent multiplayer PD experiment on small, unstructured groups30 in of 2, 3, 4 and 5 people. Note that this is not exactly the same as looking at a small lattice because in30 players formed a single group, whereas on a lattice one player shares none (von Neumann neighborhood) or two (Moore neighborhood) neighbors with her partners. Hence, increasing the number of neighbors in a lattice implies not merely increasing the number of individuals a subject plays with; it also implies an important change of the spatial structure, more specifically of the clustering coefficient (in the experiments with unstructured groups the clustering coefficient was 1). Keeping this caveat in mind, the results in30 show that the number of neighbors does not influence the behavior of the players as soon as the size of the group is 3 or more (players in a pairwise PD turned out to cooperate more as time proceeded). Then again, all our results suggests that in the experiments spatial structure does not influence the global behavior of the players. The large number of pure defectors noticed in the Madrid experiment is still puzzling and further experiments are required to address this issue. In addition, there is yet another difference we can observe: in Plön there are no players who cooperated more than 65% of the rounds, while in Madrid and Zaragoza the number of the players who cooperated more that 65% of the rounds is substantial, albeit small. The reason for this could be that in Plön the game was a strict PD, where cooperating is costly and therefore players were less prone to cooperate.
Next, we present the distribution of players according to their earnings [Figure 1 (bottom left)]. We notice that the distribution of earnings in Plön's experiment is slightly narrower. This could be the consequence of the size of the network or (more likely) the payoff matrix. Since there are not many players in the system, the earnings might be more correlated between themselves and therefore the distribution is narrower. However, the payoff matrix is also different in this experiment and as we have seen this could make players less prone to cooperate, which also narrows the earnings distribution. Finally, in Figure 1 (bottom right) we present the correlation between the earnings and the cooperativeness of the players. In all three cases there is a significant correlation (p-value < 0.001) and all three show the same trend: earnings and cooperation are anticorrelated.
Human behavior
The importance of the global results to assess the relevance of networks to promote cooperation notwithstanding, in this paper we want to focus on an issue that the three experiments considered left open, i.e., on how players actually played the PD. We will study the same three possible update strategies considered in the original papers, namely unconditional imitation or imitate-the-best20, the Fermi rule31 and moody conditional cooperation26,28. The first two of these dynamics are both examples for imitation (and thus do not lead to actions not played previously) and depend on the payoffs of the previous round, while the third one looks only at the actions of the player's partners to decide on the next action. We will analyze the possible influence of each one of these update schemes separately in what follows.
Absolute payoffs: imitate-the-best
The first update rule that has been analyzed in the previous literature is imitate-the-best. The reason for this is that in the original paper by Nowak and May20 this was the evolutionary dynamics that was used in the simulations and it led to a high level of cooperation. Imitate-the-best is a deterministic rule in which every player chooses as her next action the action of her neighbor who earned the largest payoff, including herself. In this manner, payoff differences only enter the update rule through the comparison of the payoffs with the one of the player that is deciding and the value of those differences is not relevant.
As a first step to check whether imitate-the-best is observed in the experiments, we first compute the probability that the player's action is the same as the action of the best player from the previous round. This number is rather high in all experiments (between 63% and 76%). However, since players have just two possible actions available, often the action of the focal player will coincide with the action of the best neighbor in the previous round just by chance. Importantly, we stress that even if this result were significant, it would rule out that players use (deterministic) imitate-the-best, in agreement with the observed lack of cooperation. Indeed, for unconditional imitation to promote cooperation, it has to be deterministic, i.e., a 100% imitation. If imitation is not unconditional, then noise will prevent the formation of clusters, the key mechanism observed in Nowak and May's simulations and subsequently we would not find any promotion of cooperation.
In any event, in order to test for the significance of the high levels of imitation of the player with the largest payoff found in the three experiments, we resorted to a randomization test, summarized in Fig. 2. In the plots we represent the number of players who repeated the action with the best payoff in their neighborhood a given number of rounds, both in the experiments and in an average over 1000 randomizations of their positions in the lattice. These randomizations were done by taking the time series of actions of every player and reshuffling them over the lattice, i.e., the order in the sequence of actions is preserved and only the location of players on the network is changed. Therefore, it is clear that in the randomized data, player's behavior cannot show any influence from their neighbors as they were not near each other. The results of this average are similar to those found in the experiment, suggesting that, even if there were some level of unconditional imitation in a subset of players, it would certainly be very small and not significant for the evolution of the system as a whole. Therefore, imitate-the-best does not appear to be the update strategy explaining the behavior of human subjects in spatial PDs, a conclusion that has been reached in other experiments24, although strictly speaking, our statistical analysis does not allow us to definitely rule out this strategy.
Randomization test for imitate-the-best.
Distribution of players per number of times that their actions coincide with the action of the best player in the previous round, as obtained from the experiment (bars) and as arises from 1000 randomizations of the players' positions in the lattice (solid lines). Left, Plön experiment; center, Madrid experiment and right Zaragoza experiment.
Moody conditional cooperation
Moody conditional cooperation (MCC) is a rule that was introduced in26 to describe the behavior of the subjects in the Madrid experiment. The definition of this behavioral rule contains two main ingredients: first, people cooperate more when more of their neighbors cooperated in the previous round; and second, their probability to cooperate depends on their own “mood”, to be specific, on whether they themselves cooperated or defected in the previous round. It has to be noticed that the first feature is nothing but conditional cooperation, identified in32 in one-shot public goods experiments. Figure 3 shows that MCC is observed in all three experiments: In general, after the player defected the probability of cooperating slightly decreases with the number of cooperators in the neighborhood and after the player cooperated it increases. In Plön, the behavior after the player cooperated is noticeably different than in the other two experiments, the slope being considerably larger. The probability of cooperating if the player is surrounded by defectors is much lower in Plön than in the other two experiments. This is probably a consequence of the different framing and/or the different payoff matrices used in the experiments: Since in Plön subjects played a strict PD, cooperating while surrounded by defectors was costly. Therefore, players in this experiment tend to cooperate much less when they are surrounded with defectors than in the other two experiments. As in the previous section, we need to establish the significance of this finding by comparing with what arises from randomizations of the players' location in the lattice. We present the results of this randomization in Fig. 4, using the experiment in Plön as an example (results for the other two experiments are very similar and are not shown). As can be seen from the plot, the randomization of the subjects' positions leads to the disappearance of the dependence on the context, i.e., on the number of players that cooperated in the previous round. Note that the randomizations show traces (albeit much smaller than the experiment) of MCC behavior if applied to the whole experiment, but by leaving out only the first two rounds the two lines becomes flat and the context dependence is not observed anymore. The dependence on the focal player's own choice in the previous round, which is not affected by the randomization, is still evident from the figure. We thus conclude that the evidence is strong enough to claim that all three experiments are compatible with MCC behavior.
Probability of cooperation in different contexts.
On the x-axis is the fraction of cooperating neighbors in the previous round and on the y-axis is the probability that the focal player will cooperate in the next round. We present separately the probabilities of cooperation after the focal player played C and D in the previous round. All error bars are the standard deviations of a binomial distribution,  , where n is the number of samples and p is the probability of cooperating. Straight lines are weighted fits to the data (using as weights the inverse of the variances) that take into account the number of instances of each context.
, where n is the number of samples and p is the probability of cooperating. Straight lines are weighted fits to the data (using as weights the inverse of the variances) that take into account the number of instances of each context.
Probability of cooperation in different contexts in randomized data of Plön experiment.
On the x-axis is the fraction of cooperating neighbors in the previous round and on the y-axis is the probability that the player will cooperate in the next round. We present separately the probabilities of cooperation after the focal player played C and D in the previous round. All error bars are the standard deviations of a binomial distribution,  , where n is the number of samples and p is the probability of cooperating. Left: whole experiment. Right: without the first 2 rounds. Top: experimental results. Bottom: randomized data.
, where n is the number of samples and p is the probability of cooperating. Left: whole experiment. Right: without the first 2 rounds. Top: experimental results. Bottom: randomized data.
Payoff differences: Fermi rule
An alternative proposal to understand the behavior of the participants in the experiment is the Fermi rule31,33. This is again an imitative rule, albeit with a stochastic character that not only allows for not imitating the other's behavior but also gives rise to the possibility of making mistakes. The rule is defined as follows: players pick at random one of their neighbors and copy the action they used in the previous round with a probability given by

where ΔΠ = Πi − Πj, Πi is the payoff of the player whose strategy is being updated, Πj is the payoff of the randomly chosen player to imitate, a is a normalization constant that takes into account the maximum and minimum payoff differences and β is a tunable parameter that introduces the possibility of choosing actions leading to worse payoffs. Indeed, when β = 0 the player updates her action irrespective of the payoff difference with probability 1/2, while as β → ∞ only actions leading to better payoffs are copied, with probability 1.
In Figure 5 we show the probability that the action changes depending of the payoff difference between the focal player and the best player who played the opposite action in the previous round. We see that in the Plön experiment the dependence is well fitted by the Fermi function. However, in the other two experiments, one could in principle try to fit the same expression, but the shape of the cloud of points indicates that the fitting would not be very good.
Data for the Fermi rule.
Probability of changing action in the next round as a function of the payoff difference between the focal player and the best of the players that chose the opposite action. Note that this is not exactly the Fermi update rule, because it is not possible to find out which neighbor (if any) the player chose for updating her strategy; hence, choosing the best performing one is a sensible proxy for this unknown variable. The results are presented separately for the players who changed from cooperation to defection and those who changed from defection to cooperation (see legends). Results are shown for Plön (left), Madrid (center) and Zaragoza experiments (right). The solid line in the left plot (Plön) is a fit using the analytical expression of the Fermi rule (see25 for details). All error bars are the standard deviations of a binomial distribution,  , where n is the number of samples and p is the probability of changing the action.
, where n is the number of samples and p is the probability of changing the action.
In view of the experimental data, the key issue is whether these results truly support some Fermi-like behavior or not. In that respect, it is worth mentioning that in25, even if a reasonable fit to the functional form of the rule could be obtained, it was also found that an additional high level of “spontaneous mutation” (around a 30%) was necessary to explain the changes in behavior in homogeneous neighborhoods. Therefore, it may be possible that what appears similar to a behavior described by a Fermi rule arises from some other origin. To assess this possibility, we took into account that in the previous subsection we found a dependence of the context that may also influence the results in Fig. 5. In fact, what is plotted there is the possibility to change behavior, i.e., the lower curve and the difference between 1 and the upper curve in the MCC probabilities. In addition, the payoff difference is not independent of the context.
Following this reasoning, we conjecture that the context dependence is actually a possible origin of the observed behavior. To check this hypothesis, Fig. 6 shows the data for the Plön experiment split into the five possible contexts (from zero to four cooperators) and compares it with the same randomization of spatial positions that we have used in the previous subsection. The plots reveal that, first, there is certainly a split of the putative Fermi-like curve in two parts, left and right, that arise from the fact that the probability to go from C to D is larger than that of changing from D to C; and, second, that once the context is taken away from the data, there is no dependence of the probabilities to change on the payoff differences and the experimental points are practically all within the error bars of the randomization. To obtain further confirmation of this result, we carried out agent-based simulations of the three experiments using the data on their corresponding MCC to define the agents behavior and analyzed the resulting data to see if it exhibited Fermi-like dependences. The results are plotted in Fig. 7: if one compares these plots with the original ones from the experiments in Fig. 5, it is apparent that most experimental points are within the standard deviations of the average of the simulations. Therefore, it appears that observations of Fermi-rule-like behavior may arise from MCC. In this respect, Fig. 8 shows that the opposite is not true, namely that the Fermi rule does not explain the moody conditionally cooperative behavior observed in the experiments and hence, the two explanations are not equivalent, leaving MCC as the rule most compatible with the experiments among those considered here.
Fermi rule by different contexts compared with randomized sample for Plön experiment.
Panels from from left to right and from up to bottom represent the five possible contexts (respectively, from zero to four cooperating neighbours). Solid symbols represent the observed fraction of cooperative actions after playing D (circles) and defective actions after playing C (squares), as a function of the payoff difference between the focal player and the best of her neighbours that chose the opposite action. Empty symbols represent the results of 1000 randomizations of players' positions in the lattice. The error bars represent 99% confidence interval.
Emergence of the Fermi rule in simulations of Moody conditional cooperators.
Probability of changing action in the next round as a function of the payoff difference between the focal player and the best of the players that chose the opposite action. The results are presented separately for the players who changed from cooperation to defection and those who changed from defection to cooperation (see legends). Results are obtained from simulations using the parameters of the MCC found in Plön (left), Madrid (center) and Zaragoza experiments (right). All error bars represent 99% confidence intervals. Madrid data has been binned to reduce the noise and the simulations include not only MCC but also cooperators and defectors as in the original population, to check the effect of having a truly heterogeneous population.
Emergence of MCC in simulations of the Fermi rule.
On the x-axis is the fraction of cooperating neighbors in the previous round and on the y-axis is the probability that the focal player will cooperate in the next round. We present separately the probabilities of cooperation after the focal player played C and D in the previous round. Results are obtained from simulations using the parameters of the Fermi rule found in Plön, the only case in which a good fit could be obtained. All error bars represent 99% confidence intervals.
Discussion and conclusions
Although there are several differences in the results between the three experiments, there are a few features that appear to be universal. The first one is the low but nonzero asymptotic level of cooperation. In spite of the fact that many theoretical models predict the promotion of cooperation by a mechanism of network reciprocity, such a promotion was not observed in any of the experiments analyzed here. In this paper we have only considered spatially structured populations, i.e., individuals interacting on square (planar) graphs. In other experiments23,24, performed on a smaller scale, the level of cooperation is also low. The experiments in28 extend this result to heterogeneous graphs, whereas the analysis of the well-mixed population treatment of the experiments in34 make it clear that fixed or randomly changing lattices lead to similar cooperation levels. This is further confirmed by the treatments on static networks, randomly changing networks, or dynamic networks with a low rewiring rate in35 and36. Note, however, that these papers report also experiments in which participants can choose their partner at a large rate and their cooperation emerges; this is a completely different problem and it is clear that our conclusions do not apply. Other global observables, such as the distributions of cooperation and earnings look similar, but differences between the experimental setups, such as the payoffs and the number of neighbors in the lattice, do influence the details of these distributions, most notably the percentage of cooperation. In all experiments there is a significant negative correlation between the number of cooperations and the earnings, the slopes being similar to each other. Therefore, in terms of these global observables, the present comparative analysis allows to draw two main conclusions: First, the fraction of cooperative actions is around 20–30% in lattices, not substantially higher than in well-mixed populations in any case. Second, defectors earn more than cooperators, a quantity that can be twice as large when comparing full defectors and full cooperators. It has been suggested10 that the observation that population structure does not promote cooperation may be due to the choice of payoffs for the experiments and that considering higher benefits for the cooperators could lead to different results. Even though such a setup amounts to reducing the temptation to defect and hence constitutes a weaker dilemma, the corresponding experiments should be performed to assess the generality of the conclusions obtained from the available data.
Regarding the microscopic part of our study, a frequent criticism of earlier experiments was that the systems analyzed are too small. However, in our data we find no sign that the size of the system changes the behavioral rules. We have considered the three different update rules that had been studied in the past in connection with these experiments. The detailed comparison of the outcome of the three experiments leads to a clear conclusion: a majority of players, that can be almost the whole population, behave in a way that is consistent with moody conditional cooperation (MCC). We found no evidence that subjects imitate their neighbor with the best payoff beyond what arises randomly from the lack of choice and observations of Fermi-like behavior in which players copy one neighbor's action with probability proportional to their payoffs difference can be attributed to a side effect of MCC. It is clear that the behavior of the players depends on their own previous action in all the experiments, even under randomizations of the positions of the players. Interestingly, in the experiment by Cassar23 it was also shown that the behavior of the players is significantly correlated with their previous action. The econometric analysis of the results in small groups setup of30 is also in agreement with the dependence on the previous round; at the same time, that study suggested that memory may be limited to just one round, in agreement with earlier findings by Milinski and Wedekind37 (although note that in dynamic networks with different actions per partner longer memory has been observed38, leading to similar results due to discounting behavior). As for the general features of MCC, it turns out that he probability to cooperate after having cooperated increases with the number of cooperating neighbors and is always equal to or higher than the probability to cooperate after having defected, which is only weakly depending, if at all, on the context in the previous round. Therefore, among the rules considered here, MCC is the most compatible one with the experimental results. It would be interesting to design specific experiments to put MCC to further tests and to check other alternative explanations that may be suggested. In this respect, we note MCC is a rule that would quickly become complex with increasing number of available actions; in this case, other rules similar to the Fermi one might be more applicable.
In summary, the comparative analysis of the experiments on the spatial PD presented here strongly suggests that an imposed lattice structure on a population of human subjects does not influence the global level of cooperation and also that subjects behave in a way that seems to be fully compatible with moody conditionally cooperation. Subsequent theoretical and experimental research should take these findings into account. On the theoretical side, one important conclusion that arises from the present comparative analysis is that players do not seem to take into account the payoff of their neighbors in updating their actions, focusing instead on their actions and that non-innovative rules (such as purely imitative ones that do not include mutations) are not compatible with experimental observations. Note that other contexts where non-human entities are interacting could of course be modeled with payoff-dependent rules, especially when they are subject to Darwinian evolution, but our results seem to rule this out for behavior in spatial social dilemmas involving people. It is necessary to extend this research to other games and additional experiments are needed. Very often social dilemmas do not take the form of the PD, but are coordination39, or anti-coordination/coexistence40,41,42 games, for instance. Not much is known from an experimental viewpoint about networked version of such games, although some results are available for coordination in small groups43 which suggest that networks are also not relevant to cooperation. Notwithstanding, further research is necessary in view of the predictions that topological bottlenecks may play role in the diffusion of conventions44,45 that are beyond the available results. Another important point is the extension of the experiments to people different from University students, an important issue that may46,47 or may not be relevant48 but needs more verifications. We hope that the results we are providing here for the spatial PD motivates the community to address these important and exciting open questions.
References
Maynard Smith, J. The Major Transitions in Evolution. (Oxford University Press, Oxford, 1995).
Kappeler, P. M. & van Schaik, C. P. Cooperation in Primates and Humans: Mechanisms and Evolution. (Springer, New York, 2006).
Darwin, C. The Descent of Man and Selection in Relation to Sex. (John Murray, London, 1871).
Rapoport, A. & Chammah, A. M. Prisoner's Dilemma. (University of Michigan Press, Ann Arbor, 1965).
Axelrod, R. The Evolution of Cooperation. (Basic Books, New York, 1984).
Fletcher, J. A. & Doebeli, M. A simple and general explanation for the evolution of altruism. Proc. Roy. Soc. London B 276, 13–19 (2009).
Fehr, E. & Gächter, S. Cooperation and Punishment in Public Goods Experiments. Am. Econ. Rev. 90, 980–994 (2000).
Rockenbach, B. & Milinski, M. The efficient interaction of indirect reciprocity and costly punishment. Nature 444, 718–723 (2006).
Nowak, M. A. Evolutionary dynamics: exploring the equations of life. (The Belknap Press of Harvard University Press 2006, Cambridge, Massachusetts, 2006).
Rand, D. G. & Nowak, M. A. Human cooperation. Trends Cogn. Sci. 17, 413–425 (2013).
Hamilton, W. D. The genetical evolution of social behaviour I. J. Theor. Biol. 7, 1–16 (1964).
Hamilton, W. D. The genetical evolution of social behaviour II. J. Theor. Biol. 7, 17–52 (1964).
Trivers, R. L. The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971).
Axelrod, R. & Hamilton, W. D. The evolution of cooperation. Science 211, 1390–1396 (1981).
Alexander, R. The biology of moral systems. (Aldine de Gruyter, New York, 1987).
Nowak, M. A. & Sigmund, K. Evolution of indirect reciprocity by image scoring. nature 393, 573–577 (1988).
Sigmund, K. The Calculus of Selfishness. (Princeton University Press, Princeton, 2010).
Wynne-Edwards, V. C. Evolution Through Group Selection. (Blackwell, Oxford, 1986).
Sober, E. & Wilson, D. S. Unto Others: The Evolution and Psychology of Unselfish Behavior. (Harvard University Press, Cambridge, Massachusetts, 1998).
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992).
Szabó, G. & Fáth, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Roca, C. P., Cuesta, J. & Sánchez, A. Evolutionary game theory: temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 6, 208–249 (2009).
Cassar, A. Coordination and cooperation in local, random and small world networks: Experimental evidence. Games Econ. Behav. 58, 209–230 (2007).
Kirchkamp, O. & Nagel, R. Naive learning and cooperation in network experiments. Games Econ. Behav. 58, 269–292 (2007).
Traulsen, A., Semmann, D., Sommerfeld, R. D., Krambeck, H. J. & Milinski, M. Human strategy updating in evolutionary games. Proc. Natl. Acad. Sci. USA 107, 2962–2966 (2010).
Grujić, J., Fosco, C., Araujo, L., Cuesta, J. A. & Sánchez, A. Social experiments in the mesoscale: Humans playing a spatial Prisoner's Dilemma. PLoS ONE 5, e13749 (2010).
Suri, S. & Watts, D. J. Cooperation and Contagion in Web-Based, Networked Public Goods Experiments. PLoS ONE 6(3), e16836 (2011).
Gracia-Lázaro, C., Ferrer, A., Ruiz, G., Tarancón, A., Cuesta, J., Sánchez, A. & Moreno, Y. Heterogeneous networks do not promote cooperation when humans play a Prisoner's Dilemma. Proc. Natl. Acad. Sci. USA 109, 12922–12926 (2012).
Macy, M. W. & Flache, A. Learning dynamics in social dilemmas. Proc. Nat. Acad. Sci. USA 99, 7229–7236 (2002).
Grujić, J., Eke, B., Cabrales, A., Cuesta, J. A. & Sánchez, A. Three is a crowd in iterated prisoner's dilemmas: experimental evidence on reciprocal behavior. Sci. Rep. 2, 638 (2012).
Szabó, G. & Töke, C. Evolutionary prisoner's dilemma game on a square lattice. Phys. Rev. E 58, 69–73 (1998).
Fischbacher, U., Gächter, S. & Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 71, 397–404 (2001).
Helbing, D. Interrelations between Stochastic Equations for Systems with Pair Interactions. Physica A 181, 29–52 (1992).
Grujić, J., Röhl, T., Semmann, D., Milinski, M. & Traulsen, A. Consistent Strategy Updating in Spatial and Non-Spatial Behavioral Experiments Does Not Promote Cooperation in Social Networks. PLoS ONE 7(11), e47718 (2012).
Rand, D. G., Arbesman, S. & Christakis, N. A. Dynamic social networks promote cooperation in experiments with humans. Proc. Natl. Acad. Sci. USA 108, 19193–19198 (2011).
Wang, J., Suri, S. & Watts, D. J. Cooperation and assortativity with dynamic partner updatings. Proc. Natl. Acad. Sci. USA 109, 14363–14368 (2012).
Milinski, M. & Wedekind, C. Working memory constrains human cooperation in the Prisoner's Dilemma. Proc. Natl. Acad. Sci. USA 95, 13755–13758 (1998).
Fehl, K., van der Post, D. J. & Semmann, D. Co-evolution of behaviour and social network structure promotes human cooperation. Ecol. Lett. 14, 546–551 (2011).
Skyrms, B. The Stag Hunt and Evolution of Social Structure. (Cambridge University Press, Cambridge, 2003).
Maynard Smith, J. Evolution and the Theory of Games. (Cambridge University Press, Cambridge, 1982).
Sugden, R. Economics of Rights, Cooperation and Welfare. (Palgrave Macmillan, New York, 2004).
Santos, F. C., Pacheco, J. M. & Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 103, 3490–3494.
Antonioni, A., Cacault, M. P., Lalive, R. & Tomassini, M. Coordination on Networks: Does Topology Matter?. PLoS ONE 8, e55033 (2013).
Lozano, S., Arenas, A. & Sánchez, A. Mesoscopic structure conditions the emergence of cooperation on social networks. PLoS ONE 3, e1892 (2008).
Roca, C. P., Lozano, S., Arenas, A. & Sánchez, A. Topological traps control flow on real networks: The case of coordination failures. PLoS ONE 5, e15210 (2010).
Herrmann, B., Thöni, C. & Gächter, S. Antisocial punishment across societies. Science 319, 1362–1367 (2008).
Henrich, J., Heine, S. J. & Norenzayan, A. Most people are not WEIRD. Nature 466, 1480–1484 (2010).
Exadaktylos, F., Espín, A. M. & Brañas-Garza, P. Experimental subjects are not different. Sci. Rep. 3, 1213 (2013).
Acknowledgements
J.G. is supported by CONGAS project FP7-ICT-2011-8-317672. J.A.C. and A.S. are supported by grants PRODIEVO (MINECO, Spain) and MODELICO-CM (Comunidad de Madrid, Spain). C.G.-L. and Y.M. are partially supported by MINECO through Grant FIS2011-25167; Comunidad de Aragón (Spain) through a grant to the group FENOL and by the EC FET-Proactive Project MULTIPLEX (grant 317532).
Author information
Authors and Affiliations
Contributions
J.G. and C.G.-L. analyzed the data. J.G., C.G.-L., M.M., D.S., A.T., J.A.C., Y.M. and A.S. provided original data from experiments, discussed the analyses and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Grujić, J., Gracia-Lázaro, C., Milinski, M. et al. A comparative analysis of spatial Prisoner's Dilemma experiments: Conditional cooperation and payoff irrelevance. Sci Rep 4, 4615 (2014). https://doi.org/10.1038/srep04615
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04615
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.