Abstract
Meaning has been left outside most theoretical approaches to information in biology. Functional responses based on an appropriate interpretation of signals have been replaced by a probabilistic description of correlations between emitted and received symbols. This assumption leads to potential paradoxes, such as the presence of a maximum information associated to a channel that creates completely wrong interpretations of the signals. Game-theoretic models of language evolution and other studies considering embodied communicating agents show that the correct (meaningful) match resulting from agent-agent exchanges is always achieved and natural systems obviously solve the problem correctly. Inspired by the concept of duality of the communicative sign stated by the swiss linguist Ferdinand de Saussure, here we present a complete description of the minimal system necessary to measure the amount of information that is consistently decoded. Several consequences of our developments are investigated, such as the uselessness of a certain amount of information properly transmitted for communication among autonomous agents.
Similar content being viewed by others
Introduction
Major innovations in evolution have been associated with novelties in the ways information is coded, modified and stored by biological structures on multiple scales1. Some of the major transitions involved the emergence of complex forms of communication, being human language the most prominent and difficult to explain2. The importance of information in biology has been implicitly recognized since the early developments of molecular biology, which took place simultaneously with the rise of computer science and information theory. Not surprisingly, many key concepts such as coding, decoding, transcription or translation were soon incorporated as part of the lexicon of molecular biology3.
Communication among individual cells promoted multicellularity, which required the invention and diversification of molecular signals and their potential interpretations. Beyond genetics, novel forms of non-genetic information propagation emerged. At a later stage, the rise of neural systems opened a novel scenario to interact and communicate with full richness2. Human language stands as the most complex communication system and, since communication deals with the creation, reception and processing of information, understanding communication in information theoretic terms has become a major thread in our approach to the evolution of language.
In its classical form, information theory (IT) was formulated as a way of defining how signals are sent and received through a given channel with no attention to their meaning. However, in all kinds of living systems, from cells sharing information about their external medium, individuals of a given species surviving in a world full of predators or when two humans or apes exchange signals, a crucial component beyond information is its meaningful content4. The distinction is very important, since information has been treated by theoreticians since Shannon's seminal work5 as a class of statistical object that measures correlations among sets of symbols, whereas meaning is inevitably tied to some sort of functional response with consequences for the fitness of the communicating agents. This standard scheme describing information transmission through a noisy channel5 is summarized in figure (1)a. The most familiar scenario would be described by a speaker (S) and a listener or receiver (R) having a conversation in a living room. The air carries the voice of the first and is the channel, which would be reliable (low or zero noise) if nothing except R and S were present. Instead, the channel will become more and more unreliable (noisy) as different sources of perturbation interfere. These can be very diverse, from air turbulence and children laughing to another conversation among different people. Consistently with any standard engineering design, Shannon's picture allows us to define efficient communication in terms somewhat similar to those used -for example- within electric transmission networks. In this case, a goal of the system design is minimizing the heat loss during the transmission process. Information is a (physically) less obvious quantity, but the approach taken by standard IT is quite the same.
In standard theory of information, as defined in Shannon's theory, a communication system (a) is described in terms of a sequential chain of steps connecting a source of messages (S) and a final receiver (R). The source can be considered linked to some external repertoire of objects (Ω). An encoder and a decoder participate in the process and are tied through a channel Λ, subject to noise. The acquisition and evolution of a language, as it happens in artificial systems of interacting agents, like robots (b), involves some additional aspects that are usually ignored in the original formulation of Shannon's approach. Those include the embodiment of agents and the necessary consistency in their communicative exchanges emerging from the their perceptions of the shared, external world. Picture courtesy of Luc Steels.
As a consequence of its statistical formulation, IT does not take into account “meaning” or “purpose” which, as noted by Peter Schuster1, are also difficult notions for evolutionary biology. Despite this limitation, it has been shown to successfully work in the analysis of correlations in biology6. However, one undesirable consequence of this approach is that some paradoxical situations can emerge that contradict our practical intuition. An example is that a given pair of signals s1, s2 associated to two given objects or events from the external world could be “interpreted” by the receiver of the messages in a completely wrong way –“fire” and “water”, for example, could be understood, as “water” and “fire”, respectively. Measured from standard IT -see below- the information exchanged is optimal -even perfect- if “fire” (“water”) is always interpreted as “water” (“fire”). In other words, full miscommunication can also score high, as perfectly “efficient”, within Shannon's framework. Therefore, one should approach the communicative sign as a dual entity that must be preserved as a whole in the communicative exchange. This crucial duality sign in communicative exchanges was already pointed out -with some conceptual differences to the version we will develop below-before the birth of information theory by the Swiss linguist Ferdinand de Saussure in his acclaimed Cours de linguistique générale7.
It seems obvious that meaning -and its connection to some signal, in order to create the dual entity- plays an essential role and has been shaped through evolution: “the message, the machinery processing the message and the context in which the message is evaluated are generated simultaneously in a process of coevolution”1. In our bodies, proper recognition of invaders is essential to survival and failures to recognizing the self and the non-self are at the core of many immune diseases8,9. Similarly, learning processes associated to proper identification of predators and how to differentiate them from inmates are tied to meaningful information. Beyond the specific details associated to each system, correct information storing and sharing and the relevance of meaning is well illustrated by its impact on evolutionary dynamics. As pointed out in3 we can say that, in biology, the coder is natural selection. In this way, the use of evolutionary game theoretic arguments has played a very important role in shaping evolutionary approaches to language and commmunication10,11,12,13,14,15, but require some extension in order to properly account for meaningful information. Moreover, evolutionary robotics and the artificial evolution of protolanguages and proto-grammars is a unique scenario where such a framework naturally fits16,17,18,19,20,21,22. Evolving robots capable of developing simple communication skills are able of acquiring a repertoire of appropriate signals, share them and interpret correctly the signals sent by other agents. The coherent development of a shared set of symbols that is correctly used -and thus where “meaning” is preserved- becomes central. Such coherence results from the combination of a shared repertoire of signals together with a shared perception of the external world, as detected and perceived by the same class of sensing devices.
In this paper we develop and describe an information-theoretic minimal system in which the signal is linked to a referential value. This relation is assumed to be simple and direct, so that no other process than the mapping is assumed. Other forms of more complex meaning associations would deviate from the spirit of the paper, which is to introduce the minimum framework accounting for the conservation the simplest form of meaning. In a nutshell, we are going to derive an information-theoretic measure able to grasp the consistency of the shared information between agents, when meaning is introduced as a primitive referential value attributed to one or more signals.
Results
We start this section describing the minimal system incorporating referential values for the sent signals. Within this system, we show what is meant when we say that information theory is blind to any meaning of the message. We then derive the amount of consistently decoded information between two given agents exchanging information of their shared world, thereby fixing the problem pointed out above and analyze some of its most salient properties, including the complete description of the binary symmetric channel within this new framework.
The minimal system encompassing referentiality
Our minimal system to study the referential or semantic consistency of a given information exchange will involve two autonomous communicative agents, A, B, a channel, Λ and a shared world, Ω. Agents exchange information about their shared world through the channel -see figure (2). Now we proceed to describe it in detail.
Minimal communicative system to study the conservation of referentiality (a): A shared world, whose events are the members of the set Ω and whose behavior is governed by the random variable XΩ. A coding engine, PA, which performs a mapping between Ω and the set of signals  , being Xs the random variable describing the behavior of the set of signals obtained after coding. The channel, Λ, may be noisy and, thus, the input of the decoding device, QB, depicted by
, being Xs the random variable describing the behavior of the set of signals obtained after coding. The channel, Λ, may be noisy and, thus, the input of the decoding device, QB, depicted by  , might be different from Xs. QB performs a mapping between
, might be different from Xs. QB performs a mapping between  and Ω, whose output is described by
and Ω, whose output is described by  . Whereas mutual information provides a measure of the relevance of the correlations between XΩ and
. Whereas mutual information provides a measure of the relevance of the correlations between XΩ and  , consistent information evaluates the relevance of the information provided by consistent pairs with regard to the overall amount of information. In this context, from a classical information-theoretical point of view, situations like b) and c) could be indistinguishable. By defining the so-called consistent information we can properly differentiate b) and c) by evaluating the degree of consistency of input/output pairs -see text.
, consistent information evaluates the relevance of the information provided by consistent pairs with regard to the overall amount of information. In this context, from a classical information-theoretical point of view, situations like b) and c) could be indistinguishable. By defining the so-called consistent information we can properly differentiate b) and c) by evaluating the degree of consistency of input/output pairs -see text.
Description
An agent, A, is defined as a pair of computing devices,

where PA is the coder module and QA is the decoder module. The shared world is defined by a random variable XΩ, which takes values from the set of events, Ω, Ω = {m1, …, mn}, denoting the (always non-zero) probability associated to any event mk ∈ Ω as p(mk). The coder module, PA, is described by a mapping from Ω to the set of signals:  . We will here assume
. We will here assume  , unless the contrary is indicated. The mapping that represents the coder module is defined by means of a matrix of conditional probabilities PA, whose elements
, unless the contrary is indicated. The mapping that represents the coder module is defined by means of a matrix of conditional probabilities PA, whose elements  satisfy the normalization conditions (namely, for all mi ∈ Ω,
satisfy the normalization conditions (namely, for all mi ∈ Ω,  ). The outcome of the coding process is depicted by the random variable Xs, taking values from
). The outcome of the coding process is depicted by the random variable Xs, taking values from  according to a probability distribution
according to a probability distribution

The channel Λ is characterized by the n × n matrix of conditional probabilities Λ, with matrix elements  ). The random variable
). The random variable  describes the output of the composite system world + coder + channel, thereby taking values on the set
describes the output of the composite system world + coder + channel, thereby taking values on the set  and follows the probability distribution q′, defined as
and follows the probability distribution q′, defined as

Finally, the decoder module is a computational device described by a mapping from  to Ω; i.e. it receives
to Ω; i.e. it receives  as the input set, emitted by another agent through the channel and yields as output elements of the set Ω. QA is completely defined by its transition probabilities, namely,
as the input set, emitted by another agent through the channel and yields as output elements of the set Ω. QA is completely defined by its transition probabilities, namely,  , which satisfy the normalization conditions (i.e., for all
, which satisfy the normalization conditions (i.e., for all  ,
,  ). We emphasize the assumption that, in a given agent A, following [14, 15] (but not [10, 11]) there is a priori no correlation between PA and QA.
). We emphasize the assumption that, in a given agent A, following [14, 15] (but not [10, 11]) there is a priori no correlation between PA and QA.
Now suppose that we want to study the information transfer between two agents sharing the world. Let us consider A the encoder agent and B the decoder one, although we emphasize that both agents can perform both tasks. Agent B tries to reconstruct XΩ from the information received from A. The description of Ω made by agent B is depicted by the random variable  , taking values on the set Ω and following the probability distribution p′, which takes the form:
, taking values on the set Ω and following the probability distribution p′, which takes the form:

where

From which we can naturally derive the joint probabilities,  as follows:
as follows:

We say that  is the reconstruction of the shared world, XΩ, made by agent B from the collection of messages sent by A. Summarizing, we thus have a composite system where the behavior at every step is described by a random variable, from the description of the world, XΩ to its reconstruction,
is the reconstruction of the shared world, XΩ, made by agent B from the collection of messages sent by A. Summarizing, we thus have a composite system where the behavior at every step is described by a random variable, from the description of the world, XΩ to its reconstruction,  -see figure (2a):
-see figure (2a):

At this point, it is convenient to introduce, for the sake of clarity, some new notation. We will define two matrices, namely J(AB) and Λ(AB) in such a way that  and
and  . Finally, we will define the probability distribution Λi(AB) ≡ {Λi1(AB), …, Λin(AB)}. This new notation will enable us to manage formulas in a more compact way.
. Finally, we will define the probability distribution Λi(AB) ≡ {Λi1(AB), …, Λin(AB)}. This new notation will enable us to manage formulas in a more compact way.
Information-theorethic aspects of this minimal system
First we shall explore the behaviour of mutual information in this system. Detailed definitions of information-theory functionals used in this subsection are provided in the Methods section. Under the above described framework, we have two relevant random variables: the world XΩ and the reconstruction of the world  . Its mutual information
. Its mutual information  is defined as5,23,24:
is defined as5,23,24:

The above expression has an equivalent formulation, namely

where the right side of the above equation can be identified as the Kullback-Leibler divergence between distributions J(AB) and p · q:

Within this formulation, the mutual information is the amount of accessory bits needed to describe the composite system XΩ,  taking as the reference the distribution p · q, which supposes no correlation between XΩ and
taking as the reference the distribution p · q, which supposes no correlation between XΩ and  .
.
Let us underline a feature of mutual information which is relevant for our purposes. As is well-known, max  and equality holds if there is no ambiguity in the information processing process, meaning that the process is reversible, in logical terms. Thus, every event mi ∈ Ω has to be decoded with probability 1 to some event mj ∈ Ω which, in turn, must not be the result of the coding/decoding process of any other event. In mathematical terms, this means that PA, QB, Λ ∈ Πn×n, being Πn×n the set of n × n permutation matrices, which are the matrices in which every file and column contains n − 1 elements equal to 0 and one element equal to 1 -see Methods section. It is worth emphasizing that δn×n, the n × n identity matrix is itself a permutation matrix. Notice that if Λ(AB) ≠ δ some symbol mi sent by the source is decoded as a different element mj. This shift has no impact on the information measure
and equality holds if there is no ambiguity in the information processing process, meaning that the process is reversible, in logical terms. Thus, every event mi ∈ Ω has to be decoded with probability 1 to some event mj ∈ Ω which, in turn, must not be the result of the coding/decoding process of any other event. In mathematical terms, this means that PA, QB, Λ ∈ Πn×n, being Πn×n the set of n × n permutation matrices, which are the matrices in which every file and column contains n − 1 elements equal to 0 and one element equal to 1 -see Methods section. It is worth emphasizing that δn×n, the n × n identity matrix is itself a permutation matrix. Notice that if Λ(AB) ≠ δ some symbol mi sent by the source is decoded as a different element mj. This shift has no impact on the information measure  and this is one of the reasons by which it is claimed that the content of the message is not taken into account in the standard information measure. Actually, it is straightforward to show -see Appendix B- that only n! out of the (n!)3 configurations leading to the maximum mutual information also lead to a fully consistent reconstruction -i.e., a reconstruction where referential value is conserved. This mathematically shows that, for autonomous agents exchanging messages, mutual information is a weak indicator of communicative success.
and this is one of the reasons by which it is claimed that the content of the message is not taken into account in the standard information measure. Actually, it is straightforward to show -see Appendix B- that only n! out of the (n!)3 configurations leading to the maximum mutual information also lead to a fully consistent reconstruction -i.e., a reconstruction where referential value is conserved. This mathematically shows that, for autonomous agents exchanging messages, mutual information is a weak indicator of communicative success.
Derivation of consistent information
Now we have a complete description of the minimal system able to encompass referential values for the sent signals. It is the objective of this section to derive an information-theoretic measure, different from mutual information, that will allow us to evaluate the amount of consistently decoded information.
Preliminaries
The rawest evaluation of the amount of consistently decoded pairs is found by averaging the probability of having a consistent coding/decoding process during an information exchange between agent A and agent B. This corresponds to the view of an external observer simply counting events and taking into account only whether they are consistently decoded or not. This probability, denoted as θAB, is obtained by summing the probability of having consistent input output pair, i.e.:

This formula has been widely used as a communicative payoff for an evolutionary dynamics in which consistent communication has a selective advantage11,14,15. We observe that the probability of error pe(AB) in this scenario is given by pe(AB) = 1 − θAB. Therefore, thanks to Fano's inequality -see Methods section-, we can relate this parameter to the information-theoretic functionals involved in the description of this problem, namely:

From this parameter, we can build another, a bit more elaborated functional. We are still under the viewpoint of the external observer who is now interested in the fraction of information needed to describe the composite system XΩ,  that comes from consistent input/output pairs when information is sent from A to B. This fraction, to be named σAB, is:
that comes from consistent input/output pairs when information is sent from A to B. This fraction, to be named σAB, is:

We observe that the above quantity is symmetrical in relation to XΩ and  . These two estimators provide global indicators of consistency of the information exchange.
. These two estimators provide global indicators of consistency of the information exchange.
Consistent information
However, we can go further and ask us how much of the information from the environment is consistently decoded by agentBwhen receiving data fromA. As a first step, we observe that, since Jij(AB) = p(mi)Λij(AB), we can rewrite equation (9) as:

Knowing that D(Λi(AB)||q) is the information gain associated to element mi, p(mi)D(Λi(AB)||q) is its weighted contribution to the overall information measure. If we are interested in the amount of this information that is consistently referentiated, we have to add an “extra” weight to p(mi), namely Λii(AB), which is the probability of having mi both at the input of the coding process and at the output. Thus, since

the amount of consistent information conveyed from agent A to agent B,  , will be:
, will be:

Since this is the most important equation of the text, we rewrite it using standard probability notation:

We observe that the dissipation of consistent information is due to both standard noise  and another term, which is subtracted to
and another term, which is subtracted to  , accounting for the loss of referentiality. Using equations (8, 9) and (16) we can isolate this new source of information dissipation, the referential noise, ν(AB), leading to:
, accounting for the loss of referentiality. Using equations (8, 9) and (16) we can isolate this new source of information dissipation, the referential noise, ν(AB), leading to:

Therefore, the total loss of referential information or total noise will be described as

The above expression enables us to rewrite equation (16) as:

which mimics the classical Shannon Information, now with a more restrictive noise term. Interestingly, the above expression is not symmetrical: the presented formalism distinguishes the world, XΩ, from its reconstruction,  . If we take into account that, according to the definition we provided for an autonomous communicating agent, the information can flow in both senses (A → B and B → A), we can compute the average success of the communicative exchange between A and B,
. If we take into account that, according to the definition we provided for an autonomous communicating agent, the information can flow in both senses (A → B and B → A), we can compute the average success of the communicative exchange between A and B,  , as:
, as:

 is the consistent information about the world Ω shared by agentsAandB. In contrast to the previous one, the above expression is now symmetrical,
is the consistent information about the world Ω shared by agentsAandB. In contrast to the previous one, the above expression is now symmetrical,  , because both agents share the same world, represented by XΩ. We remark that this is an information-theoretic functional between two communicating agents, it is not an information-measure between two random variables, like mutual information is. This equation quantifies the communication success between two minimal communicating agents A, B transmitting messages about a shared world.
, because both agents share the same world, represented by XΩ. We remark that this is an information-theoretic functional between two communicating agents, it is not an information-measure between two random variables, like mutual information is. This equation quantifies the communication success between two minimal communicating agents A, B transmitting messages about a shared world.
Properties
In this section we draw several important consequences from the treatment just presented, based on the consistent information concept. The rigorous and complete proofs behind them can be found in the Methods section, together with a brief discussion about the actual consistency of this measure when applied to single agents in a population (i.e., the ‘self-consistency’ or coherence that an individual agent should also keep about the world).
The binary symmetric channel
We first consider the simplest case, from which we can easily extract analytical conclusions that help us gain intuition: the Binary Symmetric Channel with uniform input probabilities. We are concerned with a world Ω having two events such that p(1) = p(2) = 1/2, two agents A and B sharing information about this world and a binary channel, Λ. The agents' and channel configuration are assumed to be of the following form:

being Λ(AB) = PAΛQB, as defined at the beginning of the results section. We will refer to  as the referential shift, which is the probability that a given event is wrongly decoded in the reconstruction of Ω. In this minimal system all functionals can be easily evaluated. First, we have that
as the referential shift, which is the probability that a given event is wrongly decoded in the reconstruction of Ω. In this minimal system all functionals can be easily evaluated. First, we have that  and that
and that  , being
, being  the entropy of a Bernouilli process having parameter
the entropy of a Bernouilli process having parameter  -see Methods section. This leads to the following expression of the consistent information:
-see Methods section. This leads to the following expression of the consistent information:

We can also easily compute σAB:

The behavior of consistently decoded information is shown in figure (3). In these plots we confronted the behavior of  ,
,  and
and  with their analogous counterparts when referentiality is taken into account, nalemy
with their analogous counterparts when referentiality is taken into account, nalemy  and σAB and ν(AB) (and η(AB)) respectively. We can observe the symmetric behavior of the first ones against
and σAB and ν(AB) (and η(AB)) respectively. We can observe the symmetric behavior of the first ones against  , which highlights the total insensibility to referentiality conservation of these classical measures. Instead, we observe that
, which highlights the total insensibility to referentiality conservation of these classical measures. Instead, we observe that  , σAB, η(AB) and ν(AB) do reflect the loss of referentiality conservation, showing a non-symmetric behavior with a generally decreasing trend as referentiality is progressively lost.
, σAB, η(AB) and ν(AB) do reflect the loss of referentiality conservation, showing a non-symmetric behavior with a generally decreasing trend as referentiality is progressively lost.
The binary symmetric channel when we enrich the communication system with a referential set shared by coder and decoder agent.
Plots correspond to the different values of the binary symmetric channel along  , the referential shift parameter, from
, the referential shift parameter, from  (total information with no loss of referentiality) to
(total information with no loss of referentiality) to  (total information with total loss of referentiality). On the left, from top to bottom, we have the classical, well known plots of
(total information with total loss of referentiality). On the left, from top to bottom, we have the classical, well known plots of  ,
,  (normalized to 1) and
(normalized to 1) and  . On the right, we have the equivalent ones accounting for the referentiality conservation, namely, on top,
. On the right, we have the equivalent ones accounting for the referentiality conservation, namely, on top,  , next, σAB and in the last plot, we have η(AB) (black line) and ν(AB) (red line). Units are given in bits. We observe that both
, next, σAB and in the last plot, we have η(AB) (black line) and ν(AB) (red line). Units are given in bits. We observe that both  (and
(and  ) have a symmetric behavior, with a minimum (maximum) at
) have a symmetric behavior, with a minimum (maximum) at  (total uncertainty). On the contrary,
(total uncertainty). On the contrary,  does not show a symmetric behavior, showing two minima, at
does not show a symmetric behavior, showing two minima, at  and at
and at  . There is a local maxima at about
. There is a local maxima at about  , which is a by-product of the combination of the loss of uncertainty of the system and a small but non-vanishable degree of referentiality conservation.
, which is a by-product of the combination of the loss of uncertainty of the system and a small but non-vanishable degree of referentiality conservation.
Decrease of information due to referential looses
One interesting consequence of equation (23) is that, except for very restricted situations, the presence of noise has a negative impact on the value of the consistent information, leading to the general conclusion that:

This latter inequality shows that, in most cases, in the absence of a designer, part of the information properly transmitted is actually useless for communication in a framework of autonomous agents. As demonstrated in the Methods section, the strict inequality holds in general. Indeed, the above relation becomes equality only in the very special case where there is perfect a matching between the two agents (i.e.: Λ(AB) = δn×n, being δn×n the n × n identity matrix.) or trivially, in the case where  .
.
But we can go further. Let us consider that we know that the system displays a given value of  and, by assumption, we also know H(XΩ). In these conditions, one can easily derive
and, by assumption, we also know H(XΩ). In these conditions, one can easily derive  by simply computing
by simply computing  . But it is possible to set a bound to the value of
. But it is possible to set a bound to the value of  as well. As in many problems of information theory, the general case is hard, even impossible to deal with. However, several approaches become viable in special but illustrative cases. Let us assume the paradigmatic configuration in which (∀mi ∈ Ω)p(mi) = 1/n and where Λ(AB) acts as a symmetric channel. In this case, we have that
as well. As in many problems of information theory, the general case is hard, even impossible to deal with. However, several approaches become viable in special but illustrative cases. Let us assume the paradigmatic configuration in which (∀mi ∈ Ω)p(mi) = 1/n and where Λ(AB) acts as a symmetric channel. In this case, we have that  , where
, where

and, therefore:

(See the Methods section for the details of the above derivations). This tells us, after some algebra, that in this framework,

Therefore, for  , we have that
, we have that  , leading to
, leading to

and, for example, for the case in which  we have that:
we have that:

The above examples enable us to illustrate the strong impact of noise on the conservation of the referential value within a communication exchange -stronger than the one predicted by standard noise.
Discussion
Shannon's information theory had a great, almost immediate impact in all sorts of areas, from engineering and genetics to psychology or language studies25. It also influenced the work of physicists, particularly those exploring the foundations of thermodynamics, who found that the entropy defined by Shannon provided powerful connections with statistical mechanics, particularly in terms of correlations. It is mainly at that level -i. e. the existence of correlations among different subsystems of a given system- that the use of information theory has proved useful. But correlations do not ensure a crucial type of coherence that seems necessary when dealing with meaningful communication: the preservation of referentiality.
In this paper we have addressed a especially relevant problem, namely the development of an information-theoretic framework able to preserve meaning. This is a first step towards a more general goal, which would involve establishing the basis for an evolutionary theory of language change including referentiality as an explicit component. We have shown that, if consistent information is considered, its value is significantly lower than mutual information in noisy scenarios. We have derived an analytical form of consistent information, which includes referential noise along with the standard noise term. Our information measure defines a non-symmetrical function and properly weights the -more strict- requirement of consistency. We have illustrated our general results by means of the analysis of a classical, minimal scenario defined by the binary symmetric channel. The approach taken here should be considered as the formally appropriate framework to study the evolution of communication among embodied agents, where the presence of consistency is inevitable due to shared perception constraints. Moreover, it might also be useful as a consistent mathematical framework to deal with cognitive-based models of brain-language evolution26,27,28. At this point, we should point out an important issue: Consistency of the communicative exchange is here evaluated between agents, not internally to a given agent talking to itself. Actually, there is no a priori any correlation between the coding and the decoding modules of a given agent. In doing so, we take the viewpoint proposed by [14] and [15]. Other approaches assumed an explicit link between the coding and decoding modules of the agent, thereby avoiding from the beginning the paradoxical situation in which two agents perfectly understand each other but, at the same time, they are not able to understand themselves [10, 11]. However, as shown in29, this situation is unlikely to occur under selective pressures, for the frameworks depicted by these earlier works. In the Methods section is shown that the proposed framework has also the same property, i.e., that the maximisation of consistent communication in a given community of agents leads to the self-consistency of each of them, without the need of imposing it externally, thereby simplifying the mathematical apparatus.
The framework we have developed is somehow inspired by Saussure's duality of sign: a (linguistic) sign is a twofold entity compounded of a signifier and a signified. However, it must be mentioned that there is a substantial difference between the theory we have developed and a Saussurean approach. According to Saussure, the relation between a signifier and a signified is fixed with respect to the linguistic community that uses the sign. “The masses have no voice in the matter and the signifier chosen by language could be replaced by no other”. Saussure adopts therefore a ‘static’ approach to the study of signs, whereas we adopt a dynamic perspective that allows us to address the possibility that different agents assign different meanings to the same symbol, in which case referentiality is not preserved. In this way we extend evolutionary game-theoretic arguments in order to derive a measure of consistency of the shared information between agents by incorporating the (non-)preservation of referentiality.
In the presented work we took the simplest possible form of meaning, namely, its referential object. However, we said nothing about the object itself. Further works might explore the inclusion in the above proposed framework an explicit quantification of meaning beyond its referential value, to rank events of the world and to refine the role of the information functional to evaluate proper communication exchanges in selective scenarios. In addition, new hallmarks beyond the agent-channel-agent should be explored, leading to new forms of information which play a role in biological organisation and which are poorly reflected in such a schema.
Methods
Definitions
Information theoretic functionals
The following definitions are intended to be minimal. We refer the interested reader to any standard textbook on information theory, such as [23] or [24].
-
Given a random variable XΩ taking values over the set Ω following a probability distribution p,
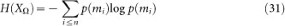
is the standard Shannon or statistical entropy.
-
Given two random variables, XΩ and
 ,
, 
is the conditional entropy of XΩ with respect
 , being, in that case,
, being, in that case, 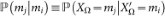 . Additionally,
. Additionally, 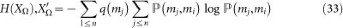
where
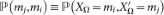 is the joint entropy of the two random variables XΩ,
is the joint entropy of the two random variables XΩ, 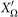 .
. -
Given two probability distributions π1, π2 defined over the set Ω, the Kullback-Leibler divergence of relative entropy of π1 with respect π2 is:

which is the amount of extra information we need to describe π1 taking as the reference distribution π2.
-
Fano's inequality. The probability of error in decoding is bounded satisfies the following inequality:

-
A Bernoulli process is a stochastic process described by a random variable X taking value in the set A = {0, 1}, being
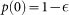 and
and 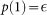 .
.  is the parameter of the Bernoulli process. Its entropy H(X) is commonly referred as
is the parameter of the Bernoulli process. Its entropy H(X) is commonly referred as  , since it only depends on this parameter:
, since it only depends on this parameter: 
Permutation matrices
A permutation matrix is a square matrix which has exactly one entry equal to 1 in each row and each column and 0's elsewhere. For example, if n = 3, we have 6 permutation matrices, namely:

The set of n × n permutation matrices is indicated as Πn×n and it can be shown that, if A ∈ Πn×n, A−1 = AT ∈ Πn×n and, if A, B ∈ Πn×n, the product AB ∈ Πn×n. Furthermore, it is clear that δn×n ∈ Πn×n, being δ the identity matrix or Kronecker symbol, defined as δij = 1 if i = j and δij = 0, otherwise.
Inequalities
We present the inequalities described in the main text in terms of three lemmas on the upper bounds of  . The first one concerns inequality (25). The second one is general and supports the third, which proves inequality (27):
. The first one concerns inequality (25). The second one is general and supports the third, which proves inequality (27):
Lemma 1.- Let AB be two agents sharing the world Ω. The Amount of consistent information transmitted from A to B -when A acts as the coder agent and B as the decoder one- satisfies that

only in the following two extreme cases:
-
1
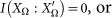 , or
, or -
2
Λ(AB) = δn×n.
Otherwise,  .
.
Proof.- The first case is the trivial one in which there is no information available due to total uncertainty -corresponding to  in the case of the symmetric binary channel studied above, see also figure (3). The second one is more interesting. Indeed, having Λ(AB) = δ means that
in the case of the symmetric binary channel studied above, see also figure (3). The second one is more interesting. Indeed, having Λ(AB) = δ means that

where we use that, if C ∈ Πn×n, C−1 = CT, also having that CT ∈ Πn×n. Out of these two situations, ∃Jik(AB) > 0, in which i ≠ k, since there are more than n non-zero entries in the matrix Λ(AB), leading to

Lemma 2.- Let AB be two agents sharing the world Ω. The Amount of consistent information transmitted from A to B -when A acts as the coder agent and B as the decoder one- is bounded as follows:

Proof.- Let  and
and  be two vectors of
be two vectors of  . Its scalar product,
. Its scalar product,  , is bounded, thanks to the so-called Hölder's inequality, in the following way:
, is bounded, thanks to the so-called Hölder's inequality, in the following way:

as long as α and β are Hölder conjugates, i.e., 1/α + 1/β = 1. The above expression can be rewritten, using the notation of norms as  -recall that, for α = β = 1/2 we recover the well-known Schwartz inequality for the euclidean distance. If we put α → 1 and β → ∞ we obtain
-recall that, for α = β = 1/2 we recover the well-known Schwartz inequality for the euclidean distance. If we put α → 1 and β → ∞ we obtain

where

being the last one the so-called Chebyshev's norm. Now we want to apply this machinery to our problem. The key point is to realize that  can be expressed as a scalar product between two vectors, having the first one coordinates J11(AB), …, Jnn(AB) and the second one D(Λ1(AB)||q), …, D(Λn(AB)||p′). We remark that this step is legitimated because all the terms involved in the computation are positive. Therefore, by applying the Hölder's inequality over the definition of
can be expressed as a scalar product between two vectors, having the first one coordinates J11(AB), …, Jnn(AB) and the second one D(Λ1(AB)||q), …, D(Λn(AB)||p′). We remark that this step is legitimated because all the terms involved in the computation are positive. Therefore, by applying the Hölder's inequality over the definition of  , we have that
, we have that

being θAB defined in equation (11). Now we observe that the probability of error in referentiating a given event of  is pe = 1 − θAB. This enables us to use Fano's inequality to bound θAB:
is pe = 1 − θAB. This enables us to use Fano's inequality to bound θAB:

thereby obtaining the desired result.
Lemma 3.- (Derivation of inequality (27)). Let AB be two agents sharing the world  and such that (
and such that ( mi ∈
mi ∈  )p(mi) = 1/n and that the channel defined by Λ(AB) is symmetric. Then, the following inequality holds:
)p(mi) = 1/n and that the channel defined by Λ(AB) is symmetric. Then, the following inequality holds:

Proof.- The first issue is to show that, if ( mi ∈ Ω)p(mi) = 1/n and the channel defined by Λ(AB) is symmetric, then
mi ∈ Ω)p(mi) = 1/n and the channel defined by Λ(AB) is symmetric, then  . Indeed, since the channel is symmetric p = p′ and thus
. Indeed, since the channel is symmetric p = p′ and thus  . Then take any mi ∈ Ω and compute D(Λi(AB)||p′):
. Then take any mi ∈ Ω and compute D(Λi(AB)||p′):

where in the third step we used the property that, in a symmetric channel, ( mi, mj ∈ Ω)
mi, mj ∈ Ω)  . Thus, if we average a constant value, we obtain such a value as the outcome (last step). Then, we apply inequality (41):
. Thus, if we average a constant value, we obtain such a value as the outcome (last step). Then, we apply inequality (41):

where, in the second step we used the fact that H(XΩ) = log n > log(n − 1) and in the third step we bound the remaining term

since  , thus completing the proof.
, thus completing the proof.
Achieving self-consistency maximizing consistent information
The structure of the functional accounting for the amount of consistent information shared by two agents -equation (21)- can lead to the paradoxical situation in which high scores on  do not imply high values of
do not imply high values of  or
or  . In brief, the degeneracy of possible optimal configurations seems to jeopardize self-understanding even in the case in which communication is optimal. Interestingly, this apparent paradox can be ruled out if we consider a population of agents, for several representative cases, as demonstrated in29 using a version of θAB. For the particular case where ηAB = 0, we have seen at the beginning of this section that
. In brief, the degeneracy of possible optimal configurations seems to jeopardize self-understanding even in the case in which communication is optimal. Interestingly, this apparent paradox can be ruled out if we consider a population of agents, for several representative cases, as demonstrated in29 using a version of θAB. For the particular case where ηAB = 0, we have seen at the beginning of this section that  , having the equality only in the special case in which Λ(AB) = δn×n, which, in turn, implies that
, having the equality only in the special case in which Λ(AB) = δn×n, which, in turn, implies that  . The interesting issue is that in the presence of three or more agents A, B and C:
. The interesting issue is that in the presence of three or more agents A, B and C:

i.e., maximizing the communicative success over a population of agents results automatically in a population of self-consistent agents, although there is no a-priori correlation between the coder and the decoder module of a given agent. Now we rigorously demonstrate this statement.
Lemma 3.- Let us have three Ai, Aj, Ak agents communicatively interacting and sharing the world  . Then, if
. Then, if  , then
, then  .
.
Proof.- We observe, as discussed above, that the premise only holds if ( i < k)
i < k)

and

Now we observe that, if  ,
,  , we conclude that:
, we conclude that:

i.e., Ak = Aj. Now, knowing that  , then:
, then:

We can easily generalize this reasoning to an arbitrarily large number of communicating agents.
References
Schuster, P. The Origin and Processing of Biological Information. Front. Life 1, 329 (2001).
Maynard Smith, J. & Száthmáry, E. The major transitions in evolution. (Oxford U. Press, Oxford, UK, 1997).
Maynard Smith, J. The Concept of Information in Biology. Phil. of Sci. 67, 177 (2000).
Hopfield, J. Physics, computation and why biology looks so different. J. Theor. l Biol. 171, 53 (1994).
Shannon, C. E. A Mathematical theory of Communication (I). Bell Syst. Tech. J. 27, 379 (1948).
Bialek, W. Biophysics: searching for principles. (Princeton University Press, Princeton, NJ, 2012).
Saussure, F. Cours de Linguistique Générale. (Bibliothèque scientifique Payot. Paris, France, 1916).
Atlan, H. Self creation of meaning. Physica Scripta 36, 563 (1987).
Atlan, H. & Cohen, I. R. Immune information, self-organization and meaning. Intl. Immunology 6, 711 (1998).
Hurford, J. Biological evolution of the Saussurean sign as a component of the language acquisition device. Lingua 77, 187 (1989).
Komarova, N. L. & Niyogi, P. Optimizing the mutual intelligibility of linguistic agents in a shared world. Art. Int. 154, 1 (2004).
Niyogi, P. The Computational Nature of Language Learning and Evolution. (MIT Press, Cambridge, Mass, 2006).
Nowak, M. A. Evolutionary Biology of Language. Phil. Trans.: Biol. Sci. 355, 1615 (2000).
Nowak, M. A. & Krakauer, D. The Evolution of Language. Proc. Nat. Acad. Sci. USA 96, 8028 (1999).
Plotkin, J. B. & Nowak, M. A. Language Evolution and Information Theory. J. Theor. Biol. 205, 147 (2000).
Cangelosi, A. & Parisi, D. Simulating the Evolution of Language. (Springer, London, UK, 2000).
Floreano, D., Mitri, S., Magnenat, S. & Keller, L. Evolutionary Conditions for the Emergence of Communication in Robots. Curr. Biol. 17, 514 (2007).
Steels, L. Language games for Autonomous Robots. IEEE Int. Syst. 16, 16 (2001).
Steels, L. & Baillie, J.-C. Shared grounding of event descriptions by autonomous robots. Robotics and Autonom. Syst. 43, 163 (2003).
Steels, L. Evolving grounded communication for robots. Trends. Cogn. Sci. 7, 308 (2003).
Steels, L. The emergence and evolution of linguistic structure: from lexical to grammatical communication systems. Connect. Sci. 17, 213 (2003).
Nolfi, S. & Mirolli, M. Evolution of Communication and Language in Embodied Agents. (Springer Verlag, Berlin, Germany, 2010).
Ash, R. B. Information Theory. (New York, Dover, NY, 1990).
Cover, T. M. & Thomas, J.-A. Elements of Information Theory (John Wiley and Sons, New York, NY, 2001).
Gleick, J. The information: A history, a theory, a flood. (Vintage, New York, NY, 2012).
Bickerton, D. Language and Species. (Chicago University Press, Chicago, IL, 1990).
Christiansen, M.-H. & Kirby, S. Language Evolution: Consensus and Controversies. Trends. Cogn. Sci. 7, 300 (2003).
Deacon, T. W. The Symbolic Species: The Co-Evolution of Language and the Brain (Norton, New York, NY, 1997).
Corominas-Murtra, B. & Solé, R. V. Nework Topology and self-consistency in Language Games. J. Theor. Biol. 241, 438 (2006).
Acknowledgements
We thank Kepa Ruiz-Mirazo, Álvaro Corral and the members of the CSL for useful discussions. This work was supported by the Fundación Botin, the Santa Fe Institute (R.V.S.), the Austrian Fonds zur Förderung der Wissenschaftlichen Forschung project “Quantifying socioeconomic multiplex networks in a massive multiplayer online game” KPP23378FW (B.C.-M.) and the Secretary for Universities and Research of the Ministry of Economy and Knowledge of the Government of Catalonia and the Cofund programme of the Marie Curie Actions of the 7th R&D Framework Programme of the European Union and the research projects 2009SGR1079, FFI201123356 (J.F.).
Author information
Authors and Affiliations
Contributions
B.C.-M., J.F. and R.S. designed research, made analytic derivations and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Corominas-Murtra, B., Fortuny, J. & Solé, R. Towards a mathematical theory of meaningful communication. Sci Rep 4, 4587 (2014). https://doi.org/10.1038/srep04587
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04587
This article is cited by
-
Orbital angular momentum-encoded quantum digital signature over atmospheric channel
Quantum Information Processing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







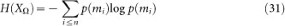
 ,
, 
 , being, in that case,
, being, in that case, 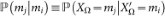 . Additionally,
. Additionally, 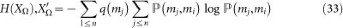
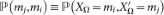 is the joint entropy of the two random variables XΩ,
is the joint entropy of the two random variables XΩ, 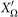 .
.

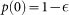 and
and 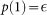 .
.  is the parameter of the Bernoulli process. Its entropy H(X) is commonly referred as
is the parameter of the Bernoulli process. Its entropy H(X) is commonly referred as  , since it only depends on this parameter:
, since it only depends on this parameter: 
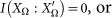 , or
, or