Abstract
Current induced spin-orbit effective magnetic fields in metal/ferromagnet/oxide trilayers provide a new way to manipulate the magnetization, which is an alternative to the conventional current induced spin transfer torque arising from noncollinear magnetization. Ta/CoFeB/MgO structures are expected to be useful for non-volatile memories and logic devices due to its perpendicular anisotropy and large current induced spin-orbit effective fields. However many aspects such as the angular and temperature dependent phenomena of the effective fields are little understood. Here, we evaluate the angular and temperature dependence of the current-induced spin-orbit effective fields considering contributions from both the anomalous and planar Hall effects. The longitudinal and transverse components of effective fields are found to have strong angular dependence on the magnetization direction at 300 K. The transverse field decreases significantly with decreasing temperature, whereas the longitudinal field shows weaker temperature dependence. Our results reveal important features and provide an opportunity for a more comprehensive understanding of current induced spin-orbit effective fields.
Similar content being viewed by others
Introduction
In-plane current induced magnetization switching1,2,3,4,5,6, fast domain wall motion7,8,9,10,11,12 and high frequency magnetization oscillation13,14,15 have been demonstrated by utilizing the newly discovered current induced spin-orbit effective fields in magnetic multilayers, especially in heavy metal/perpendicularly magnetized ferromagnet/oxide trilayers. In contrast to the conventional spin transfer torque which exploits the noncollinear magnetization in metallic spin valves and magnetic tunnel junctions16,17, in-plane current induced spin-orbit effective fields in trilayers exploit the spin-orbit coupling to generate a torque even on the collinear homogeneous ferromagnetic layer. Since trilayers have broken structural inversion symmetry and contain a heavy metal layer, such as Pt or Ta, with a strong atomic spin-orbit coupling, both the spin Hall effect2,3,8,10 and the Rashba spin-orbit interaction1,7,18,19,20,21 can be relevant in terms of symmetry and are proposed as the underlying mechanisms of the effective fields. The current induced spin-orbit effective fields can be decomposed into two components3,18,21,22,23,24 such as the longitudinal field (HL) along  direction and the transverse field (HT) along
direction and the transverse field (HT) along  direction, where
direction, where  is the magnetization and
is the magnetization and  is the directional unit vector (transverse to the current and in the film plane). Recent studies show that the size and even the sign of both HL and HT depend on the heavy metal layer thickness22 and the capping layer thickness25, suggesting complex underlying mechanisms contributing to these effective fields. Complex angular dependences of current induced spin-orbit effective fields reported in AlOx/Co/Pt and MgO/CoFeB/Ta systems emphasize the prominent role of interfaces26. These results suggest that current induced spin-orbit effective fields are still at the early stage of understanding. In order to achieve a better understanding of current induced effective fields, one should go beyond the symmetry perspective and more quantitative comparison is required between experiments and theories. In this respect, the detailed angle dependent characterizations of the fields at different temperatures are of great importance.
is the directional unit vector (transverse to the current and in the film plane). Recent studies show that the size and even the sign of both HL and HT depend on the heavy metal layer thickness22 and the capping layer thickness25, suggesting complex underlying mechanisms contributing to these effective fields. Complex angular dependences of current induced spin-orbit effective fields reported in AlOx/Co/Pt and MgO/CoFeB/Ta systems emphasize the prominent role of interfaces26. These results suggest that current induced spin-orbit effective fields are still at the early stage of understanding. In order to achieve a better understanding of current induced effective fields, one should go beyond the symmetry perspective and more quantitative comparison is required between experiments and theories. In this respect, the detailed angle dependent characterizations of the fields at different temperatures are of great importance.
The discovery of perpendicular anisotropy in Ta/CoFeB/MgO structures27 is not only a novel building block for spin transfer torque based applications, but also of significance for the study and application of current induced spin-orbit effective fields. In-plane current injection in Ta/CoFe(B)/MgO structures drives higher efficient magnetization switching and domain wall motion with opposite polarity compared to that in Pt/CoFe(B)/MgO2,8, which indicates larger and opposite current induced spin-orbit effective fields in Ta based trilayers compared to those based in Pt. These observations are consistent with the opposite signs of spin Hall angles in Ta and Pt. However, the magnitude of the spin Hall angle in Ta is still under debate. While some group reports larger spin Hall angle for Ta than Pt2, some other group find otherwise28,29. It should be noted that both the longitudinal and transverse effective fields can exert a torque on the magnetization and influence the spin dynamic process and each of the field components has been suggested to originate from different underlying mechanisms22,26. The coexistence of both the longitudinal and transverse effective fields in Ta/CoFeB/MgO offers an ideal system to study both effective field components22,26, in contrast to Pt based trilayers, in which the transverse field is still controversial among reports with some having reported it to be very small or negligible3,9.
Here we measure the angular and temperature dependence of current induced spin-orbit effective fields from Ta/CoFeB/MgO nanowires using a lock-in technique22,30. Analytical formulae have been developed in the Cartesian coordinate system to evaluate the current-induced effective fields with consideration of both the anomalous and planar Hall effects. Using vector measurements the decomposed transverse field (HT) is found to be larger than the longitudinal field (HL) at 300 K and both HT and HL have a strong dependence on the magnetization direction. The respective effective field (HT or HL) direction in Ta/CoFeB/MgO is opposite compared to that of Pt/CoFeB/MgO (Supplementary Information S5). Upon decreasing the temperature, the strength of both field components decreases, but their directions remain unchanged and HT shows stronger temperature dependence than HL.
Results
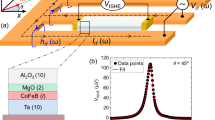
The stacked film is of the form, Si substrate/Ta (2)/Co40Fe40B20 (0.8)/MgO (2)/SiO2 (3) (nominal thicknesses in nm) grown by high vacuum (<2 × 10−9 Torr) magnetron sputtering. The film is annealed at 170°C for one hour to obtain good perpendicular anisotropy. The films are patterned into Hall bars with dimension 600 nm × 600 nm by e-beam lithography as shown in Fig. 1(a). The geometry of the transport measurements is shown in Fig. 1(b). Due to the perpendicular magnetic anisotropy of the Ta/CoFeB/MgO system27, the easy axis of the magnetization in the CoFeB layer is oriented along the out-of-plane direction, as proved by the anomalous Hall loop in Fig. 1(c), where the magnetic field is applied along the out-of-plane direction. Figure 1(d) shows the current induced switching in a Ta/CoFeB/MgO nanowire with a 400 Oe external magnetic field applied along the current direction. The anomalous Hall signal (RH) can be changed between a high and a low resistance state by injecting an in-plane current, indicating the magnetization switching of the CoFeB layer between the Mz > 0 and Mz <0 states. The switching current is ~0.11 mA which corresponds to a current density of 6.55 × 106 A/cm2 assuming the current is flowing uniformly throughout the Ta/CoFeB layer. The magnitude of switching current density is comparable to the spin transfer torque induced switching in MgO based current perpendicular to plane (CPP) magnetic tunnel junction (MTJ) nanopillars27,31, demonstrating an alternative for future high density memories and logic devices. The abrupt magnetization switching characteristics in Fig. 1(c) and (d), either by field or current, indicate well-defined perpendicular anisotropy of the device.
Device schematic, magnetic property and current-induced switching of Ta/CoFeB/MgO nanowire.
(a), Scanning electron micrograph of the device. (b), Measurement geometry in the Cartesian coordinate system. (c), Hall resistance RH as a function of H applied to out-of-plane direction at 300 K. (d), RH as a function of current with a 400 Oe magnetic field applied along the current direction at 300 K.
Two measurement schemes and current induced spin-orbit effective fields
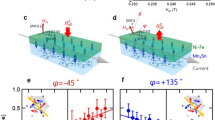
In order to quantify the current induced spin-orbit effective fields, we measure the anomalous Hall voltage loops using a harmonic technique. A sinusoidal current Iac with the amplitude of 28.3 μA and the frequency of 13.7 Hz is applied to the nanowires and the first and second harmonic signals (Vf and V2f, respectively) are measured simultaneously by two lock-in amplifiers. Each data point averages over 40 readings to reduce the noise. The Joule heating effect induced by currents is negligible (Supplementary Information S4). The measurements are performed in two measurement schemes separately, such as the longitudinal and the transverse scheme as illustrated in Fig. 2(a) and 2(b), respectively. Different from the previous studies22,30, where the magnetic field is swept below the coercive field, we sweep the magnetic field in a wider range so that the magnetization becomes saturated in the film plane for the large sweeping fields. In both schemes, the external magnetic field is applied with a small tilting angle θH to the film plane. In the longitudinal scheme in Fig. 2(a), both the ac current and magnetic field are applied along the x-direction. The anomalous Hall loops measured in the longitudinal scheme are shown in Fig. 2(c). With field sweeps along the current flow direction, the second harmonic signal  shows a negative peak at a positive magnetic field and a positive peak at a negative magnetic field. For the transverse scheme, the magnetic field is applied along the y-direction perpendicular to the current flow, as shown in Fig. 2(b). Figure 2(d) shows the anomalous Hall loops in the transverse configuration, in which the second harmonic signal
shows a negative peak at a positive magnetic field and a positive peak at a negative magnetic field. For the transverse scheme, the magnetic field is applied along the y-direction perpendicular to the current flow, as shown in Fig. 2(b). Figure 2(d) shows the anomalous Hall loops in the transverse configuration, in which the second harmonic signal  shows a negative peak for both polarities of the magnetic field.
shows a negative peak for both polarities of the magnetic field.
Schematics of two measurement schemes and current induced spin-orbit effective fields.
(a), (b), Directions of HL and HT with H along and transverse to Iac. First and second harmonic loops under these two schemes are shown in (c), (d), measured at θH = 4° and 300 K. (e) and (f) show the fitting of second harmonic voltage curves. The fitted HL and HT values are indicated in the graphs.
The second harmonic signal V2f is induced by the ac current of frequency f which exerts a periodic effective field on the magnetization, so that the magnetization oscillates around the equilibrium direction with an oscillation amplitude of Δθ and Δϕ. Combined with the anomalous Hall effect (AHE), which depends on θ and with the planar Hall effect (PHE), which depends both on θ and ϕ, the oscillation generates the second harmonic Hall voltage V2f. In the Cartesian coordinate system as defined in Fig. 1(b), the relationship between the second harmonic voltage ( and
and  ), magnetization direction (θ and ϕ) and oscillation amplitude (Δθ and Δϕ) can be written as (Supplementary Information S1)
), magnetization direction (θ and ϕ) and oscillation amplitude (Δθ and Δϕ) can be written as (Supplementary Information S1)

Since the magnetization oscillations (Δθ, Δϕ) are induced by current induced effective fields, the values of Δθ and Δϕ are determined by the strengths of effective fields, HL and HT. The relationships among θ, ϕ, Δθ, Δϕ, HL and HT are obtained by solving the force balance equations (Supplementary Information S2).
With the formulae derived above, we first attempt to fit the V2f curves by assuming constant values of HL and HT independent of the magnetization direction. This assumption will be removed later to examine the angular dependence of the effective fields. Figures 2(e, f) show the best fits under this assumption with known device parameters of RAHE = 7.42 Ω and RPHE = 0.43 Ω. Values of HL = −7.4 Oe, HT = −32.7 Oe and Han = 4550 Oe are obtained, which correspond to HL = −440 Oe and HT = −1942 Oe at 108 A/cm2 (see Supplementary S3 for the detailed fitting procedures). The directions of HL and HT are consistent with previous reports2,6,8,26. The influence of planar Hall effect is important as discussed previously26 and also in Supplementary Information S7, since its neglect results in underestimation of HL and HT. The maximum Oersted field generated from the applied ac current is about 0.2 Oe in the opposite direction to HT. The anomalous Nernst effect (ANE) is also evaluated26 (see Supplementary Information S8). The contributions from the Oersted field and ANE are negligibly small and excluded from our evaluation of the fields. It should be noted that the ratio of  is similar to the previous reports from a Ta/CoFeB/MgO structure22 and Co/Pd multilayers23, but quite different from a previous study26. Away from the dip, the fitted curve, especially the one for
is similar to the previous reports from a Ta/CoFeB/MgO structure22 and Co/Pd multilayers23, but quite different from a previous study26. Away from the dip, the fitted curve, especially the one for  in Fig. 2(f), deviates from the experimental data. The deviation suggests that, contrary to the assumption, the current induced spin-orbit effective fields have an angular dependence on the magnetization direction.
in Fig. 2(f), deviates from the experimental data. The deviation suggests that, contrary to the assumption, the current induced spin-orbit effective fields have an angular dependence on the magnetization direction.
Angular and temperature dependence of current induced spin-orbit effective fields
The previous studies have tried the linear fitting method with assuming angle-independent HL and HT for the high θ range22,30. In order to study the angular dependence of current induced spin-orbit effective fields, we calculate the effective fields at each magnetic field (see Supplementary S3 for the detailed calculation procedures). With the conversion of the magnetic field into θ using the first harmonic Hall voltage, we obtain the angular dependence of current induced effective fields at 300 K, as shown in Fig. 3(a, b). Indeed both HL and HT depend on θ and are consistent with a recent report26, which also showed strong angular dependence of both effective fields. It should be noted that the studied range of θ (10 ~ 80°) in our work is wider than the previous study (30 ~ 80° in our geometry). An interesting observation is that when the magnetization lies toward the plane of a ferromagnet layer (θ = 10 ~ 30°), both HL and HT increase more rapidly and show different angular dependence as compared to a monotonic dependence in the high θ range (40 ~ 80°). This suggests the effective fields have different angular dependence at low and high angle regions.
The harmonic loops are also measured at different temperatures in order to study the temperature dependence of HL and HT. First we adopt the same strategy as in Fig. 2(e, f) by assuming constant values of HL and HT to evaluate the effective fields at different temperatures. Variations of RAHE, RPHE and Han with temperature are considered (see Supplementary Information S3). The results are shown in Fig. 4(a). HL changes from −7.4 Oe at 300 K to −4.9 Oe at 50 K, while HT shows a more rapid decrease from −32.7 Oe at 300 K to −2.77 Oe at 50 K. We compare the temperature dependence of HL with the current induced switching current IS, since current induced switching is mainly driven by HL1,3,32. As seen from Fig. 4(b), the temperature dependence of HL/Han shows a similar trend with 1/IS. When temperature changes from 300 to 50 K, HL/Han decreases 3.6 times and 1/IS decrease 4.8 times, whereas HT/Han in the inset of Fig. 4(b) shows a change more than one order within the temperature range. The small difference between the change of HL/Han and 1/IS with temperature indicates HT may also play a role in the current induced switching.
Temperature dependence of current induced spin-orbit effective fields.
(a), HL and HT (assuming constant values independent of magnetization direction) at θH = 4° at different temperatures. (b), Comparison of |1/IS| (with 400 Oe assisted field along current direction) and |HL/Han| at different temperatures. The inset shows the temperature dependence of |HT/Han|. (c), HL vs. θ at different temperatures. (d), HT vs. θ at different temperatures. The insets in (c), (d) show the fits of second harmonic voltage curves by assuming angle-independent effective fields at 100 K, with the parameters of HL = −4.85 Oe, HT = −7.50 Oe and Han = 9800 Oe.
Angular dependence of HL and HT at different temperatures are also shown in Fig. 4(c, d). Fluctuations at large θ in Fig. 4(c), especially at low temperatures (50 and 100 K), can be attributed to the small second harmonic signals, when magnetization is close to the out-of-plane direction at low fields. Overall both HL and HT are found to decrease with decreasing temperature at different θ and a stronger dependence on θ is observed at higher temperatures. An interesting observation is that HL becomes angular independent for the studied range of θ at 50 and 100 K, but shows a weak angular dependence for θ < 15° at 150 K. In the inset of Fig. 4(c), a fit for the  data (mainly originates from HL) at 100 K by assuming field-independent effective fields shows good match at each magnetic field, verifying HL is angular independent at 100 K. On the other hand, the fitting to the experimental
data (mainly originates from HL) at 100 K by assuming field-independent effective fields shows good match at each magnetic field, verifying HL is angular independent at 100 K. On the other hand, the fitting to the experimental  data at 100 K shows large deviation as shown in the inset of Fig. 4(d), suggesting HT is angular dependent at 100 K although its magnitude becomes much smaller compared to that at 300 K. A theoretical model is required to explain the observed complex temperature and angular dependence in current induced spin-orbit effective fields.
data at 100 K shows large deviation as shown in the inset of Fig. 4(d), suggesting HT is angular dependent at 100 K although its magnitude becomes much smaller compared to that at 300 K. A theoretical model is required to explain the observed complex temperature and angular dependence in current induced spin-orbit effective fields.
Discussion
Quite different temperature dependence of HL and HT may indicate the possibility of different origins for these two effective field components. Indeed, HL is often argued to arise mainly from the spin Hall effect3,8,33,34, while HT mainly from the Rashba interaction effect1,6,7,18,21. Assuming the spin Hall effect is the origin of HL, the relation between HL and the spin Hall angle θSH is given by  , where e is the electron charge, MS = 106 A/m is the saturation magnetization and tF = 0.8 nm is the ferromagnet thickness24,35. By using the HL value of −7.4 Oe (corresponding to −440 Oe per 108 A/cm2) in Fig. 2(e, f), θSH of Ta is estimated to be −0.11 at 300 K which is close to the reported value of −0.122. However, as the Ta thickness (tTa) is 2 nm in our structure, the spin diffusion term (1 − sec h(tTa/λTa)) should be considered to extract θSH, which enlarges θSH of Ta to −0.26 by using λTa = 1.8 nm from a recent report36. The small decrease of HL as temperature decreases can be related to the enhancement of MS and small variation of θSH at lower temperatures37. However, the currently established spin Hall model cannot explain the angular dependence of HL. Therefore, either an extended spin Hall scenario or another mechanism is required to fully describe the temperature and angular dependence of HL. Similarly, the features of HT in this study cannot be explained by the currently established Rashba interaction model, which assumes the transverse field to be angle-independent18,33 or weakly dependent38. Thus it fails to describe the observed angular dependence of HT. The temperature dependence of HT also presents challenge for theories, since HT decreases significantly with lowering temperature and becomes negligible at 50 K, suggesting the possibility that it may be related thermally induced excitation process39. If the Rashba interaction is considered to be responsible for HT, our observations call for an extension or modification of the model to include a temperature dependence, which lacks at this moment. Recently it has been proposed that the imaginary part of the spin mixing conductance can result in HT40. However, as the spin mixing conductance is little influenced by temperature41, the spin mixing conductance scenario fails to explain the temperature dependence of HT. Nonetheless, since HT is a few times larger than HL at room temperature and increases more rapidly with increasing temperature, HT can play an important role for practical device applications. Recently, HT has been reported from in-plane magnetization Pt/NiFe structures and utilized for magnetization switching4.
, where e is the electron charge, MS = 106 A/m is the saturation magnetization and tF = 0.8 nm is the ferromagnet thickness24,35. By using the HL value of −7.4 Oe (corresponding to −440 Oe per 108 A/cm2) in Fig. 2(e, f), θSH of Ta is estimated to be −0.11 at 300 K which is close to the reported value of −0.122. However, as the Ta thickness (tTa) is 2 nm in our structure, the spin diffusion term (1 − sec h(tTa/λTa)) should be considered to extract θSH, which enlarges θSH of Ta to −0.26 by using λTa = 1.8 nm from a recent report36. The small decrease of HL as temperature decreases can be related to the enhancement of MS and small variation of θSH at lower temperatures37. However, the currently established spin Hall model cannot explain the angular dependence of HL. Therefore, either an extended spin Hall scenario or another mechanism is required to fully describe the temperature and angular dependence of HL. Similarly, the features of HT in this study cannot be explained by the currently established Rashba interaction model, which assumes the transverse field to be angle-independent18,33 or weakly dependent38. Thus it fails to describe the observed angular dependence of HT. The temperature dependence of HT also presents challenge for theories, since HT decreases significantly with lowering temperature and becomes negligible at 50 K, suggesting the possibility that it may be related thermally induced excitation process39. If the Rashba interaction is considered to be responsible for HT, our observations call for an extension or modification of the model to include a temperature dependence, which lacks at this moment. Recently it has been proposed that the imaginary part of the spin mixing conductance can result in HT40. However, as the spin mixing conductance is little influenced by temperature41, the spin mixing conductance scenario fails to explain the temperature dependence of HT. Nonetheless, since HT is a few times larger than HL at room temperature and increases more rapidly with increasing temperature, HT can play an important role for practical device applications. Recently, HT has been reported from in-plane magnetization Pt/NiFe structures and utilized for magnetization switching4.
In conclusion, we report strong angle and temperature dependence of in-plane current induced spin-orbit effective fields. An analytical framework is developed in the Cartesian coordinate system to evaluate current induced spin-orbit effective fields from low frequency harmonic Hall voltage measurements. Our results illustrate the complex characteristics of the spin-orbit effective magnetic fields depending on the direction of magnetization and temperature. However, these results cannot be completely explained by either the spin Hall or Rashba interaction models and call for a new model of current induced effective fields. As the origin of the effective fields is still under intense debate, the angle and temperature dependent characterization of these fields reveals detailed features of the current induced effective fields in metal/ferromagnet/oxide trilayers and allows optimizing the effect for future spin-orbit based spintronic devices.
References
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L. Q. et al. Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum. Science 336, 555–558 (2012).
Liu, L. Q., Lee, O. J., Gudmundsen, T. J., Ralph, D. C. & Buhrman, R. A. Current-Induced Switching of Perpendicularly Magnetized Magnetic Layers Using Spin Torque from the Spin Hall Effect. Phys. Rev. Lett. 109, 096602 (2012).
Fan, X. et al. Observation of the nonlocal spin-orbital effective field. Nat. Commun. 4, 1799 (2013).
Avci, C. O. et al. Magnetization switching of an MgO/Co/Pt layer by in-plane current injection. Appl. Phys. Lett. 100, 212404 (2012).
Suzuki, T. et al. Current-induced effective field in perpendicularly magnetized Ta/CoFeB/MgO wire. Appl. Phys. Lett. 98, 142505 (2011).
Miron, I. M. et al. Fast current-induced domain-wall motion controlled by the Rashba effect. Nat. Mater. 10, 419–423 (2011).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Emori, S., Bono, D. C. & Beach, G. S. D. Interfacial current-induced torques in Pt/Co/GdOx. Appl. Phys. Lett. 101, 042405 (2012).
Haazen, P. P. J. et al. Domain wall depinning governed by the spin Hall effect. Nat. Mater. 12, 299–303 (2013).
Chiba, D. et al. Electric-field control of magnetic domain-wall velocity in ultrathin cobalt with perpendicular magnetization. Nat. Commun. 3, 888 (2012).
Moore, T. A. et al. High domain wall velocities induced by current in ultrathin Pt/Co/AlOx wires with perpendicular magnetic anisotropy. Appl. Phys. Lett. 93, 262504 (2008).
Liu, L. Q., Pai, C. F., Ralph, D. C. & Buhrman, R. A. Magnetic Oscillations Driven by the Spin Hall Effect in 3-Terminal Magnetic Tunnel Junction Devices. Phys. Rev. Lett. 109, 186602 (2012).
Demidov, V. E. et al. Magnetic nano-oscillator driven by pure spin current. Nat. Mater. 11, 1028–1031 (2012).
Liu, R. H., Lim, W. L. & Urazhdin, S. Spectral Characteristics of the Microwave Emission by the Spin Hall Nano-Oscillator. Phys. Rev. Lett. 110, 147601 (2013).
Ralph, D. C. & Stiles, M. D. Spin transfer torques. J. Magn. Magn. Mater. 320, 1190–1216 (2008).
Brataas, A., Kent, A. D. & Ohno, H. Current-induced torques in magnetic materials. Nat. Mater. 11, 372–381 (2012).
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 9, 230–234 (2010).
Pesin, D. A. & MacDonald, A. H. Quantum kinetic theory of current-induced torques in Rashba ferromagnets. Phys. Rev. B 86, 014416 (2012).
Kim, K. W., Seo, S. M., Ryu, J., Lee, K. J. & Lee, H. W. Magnetization dynamics induced by in-plane currents in ultrathin magnetic nanostructures with Rashba spin-orbit coupling. Phys. Rev. B 85, 180404 (2012).
Wang, X. H. & Manchon, A. Diffusive Spin Dynamics in Ferromagnetic Thin Films with a Rashba Interaction. Phys. Rev. Lett. 108, 117201 (2012).
Kim, J. et al. Layer thickness dependence of the current-induced effective field vector in Ta|CoFeB|MgO. Nat. Mater. 12, 240–245 (2013).
Jamali, M. et al. Spin-orbit torques in Co/Pd multilayer nanowires. Phys. Rev. Lett. 111, 246602 (2013).
Seo, S.-M., Kim, K.-W., Ryu, J., Lee, H.-W. & Lee, K.-J. Current-induced motion of a transverse magnetic domain wall in the presence of spin Hall effect. Appl. Phys. Lett. 101, 022405 (2012).
Qiu, X. et al. A new route to spin-orbit torque engineering via oxygen manipulation. e-print arXiv:1311.3032 (2013).
Garello, K. et al. Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Morota, M. et al. Indication of intrinsic spin Hall effect in 4d and 5d transition metals. Phys. Rev. B 83, 174405 (2011).
Tanaka, T. et al. Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals. Phys. Rev. B 77, 165117 (2008).
Pi, U. H. et al. Tilting of the spin orientation induced by Rashba effect in ferromagnetic metal layer. Appl. Phys. Lett. 97, 162507 (2010).
Ikeda, S. et al. Magnetic tunnel junctions for spintronic memories and beyond. IEEE. Trans. Electron. Dev. 54, 991–1002 (2007).
Lee, K. S., Lee, S. W., Min, B. C. & Lee, K. J. Threshold current for switching of a perpendicular magnetic layer induced by spin Hall effect. Appl. Phys. Lett. 102, 112410 (2013).
Haney, P. M., Lee, H. W., Lee, K. J., Manchon, A. & Stiles, M. D. Current induced torques and interfacial spin-orbit coupling: Semiclassical modeling. Phys. Rev. B 87, 174411 (2013).
Manchon, A. Spin Hall effect versus Rashba torque: a Diffusive Approach. e-print arXiv:1204.4869 (2012).
Khvalkovskiy, A. V. et al. Matching domain-wall configuration and spin-orbit torques for efficient domain-wall motion. Phys. Rev. B 87, 020402 (2013).
Hahn, C. et al. Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta. Phys. Rev. B 87, 174417 (2013).
Vila, L., Kimura, T. & Otani, Y. Evolution of the spin Hall effect in Pt nanowires: Size and temperature effects. Phys. Rev. Lett. 99, 226604 (2007).
Ortiz Pauyac, C., Wang, X., Chshiev, M. & Manchon, A. Angular dependence and symmetry of Rashba spin torque in ferromagnetic heterostructures. Appl. Phys. Lett. 102, 252403 (2013).
Guo, Z. B. et al. Effects of surface and interface scattering on anomalous Hall effect in Co/Pd multilayers. Phys. Rev. B 86, 104433 (2012).
Chen, Y.-T. et al. Theory of spin Hall magnetoresistance. Phys. Rev. B 87, 144411 (2013).
Czeschka, F. D. et al. Scaling Behavior of the Spin Pumping Effect in Ferromagnet-Platinum Bilayers. Phys. Rev. Lett. 107, 046601 (2011).
Acknowledgements
This work is partially supported by the Singapore National Research Foundation under CRP Award No. NRF-CRP 4-2008-06, NRF (NRF-2013R1A2A2A01013188), KU-KIST School Joint Research Program, NRF (NRF-2013R1A2A2A05006237) and MOTIE (Grant No. 10044723).
Author information
Authors and Affiliations
Contributions
X.Q. and H.Y. conceived the experiments. X.Q. and K.N. carried out experiments. X.Q., P.D. and K.-S.L. did modeling. X.Q., K.L., H.L. and H.Y. wrote the manuscript. All authors discussed the data and the results and commented the manuscript. H.Y. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary info
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Qiu, X., Deorani, P., Narayanapillai, K. et al. Angular and temperature dependence of current induced spin-orbit effective fields in Ta/CoFeB/MgO nanowires. Sci Rep 4, 4491 (2014). https://doi.org/10.1038/srep04491
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04491
This article is cited by
-
Improved spin–orbit torque induced magnetization switching efficiency by helium ion irradiation
Scientific Reports (2022)
-
Efficient conversion of orbital Hall current to spin current for spin-orbit torque switching
Communications Physics (2021)
-
Hall-bar-width dependence of the field-like spin-orbit torque in NiFe/Pt bilayers
Journal of Superconductivity and Novel Magnetism (2021)
-
Experimental Determination of the Orientation of Tilted Magnetic Anisotropy by Using Angle-Resolved Hall Effect Signals
Journal of Superconductivity and Novel Magnetism (2021)
-
Thermal behavior of spin-current generation in PtxCu1-x devices characterized through spin-torque ferromagnetic resonance
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.