Abstract
Electronic and phonon coherence are usually measured in different ways because their time-scales are very different. In this paper we simultaneously measure the electronic and phonon coherence using the interference of the electron-phonon correlated states induced by two phase-locked optical pulses. Interferometric visibility showed that electronic coherence remained in a semiconducting GaAs crystal until ~40 fs; in contrast, electronic coherence disappeared within 10 fs in a semimetallic Bi crystal at room temperature, differing substantially from the long damping time of its phonon coherence, in the picosecond range.
Similar content being viewed by others
Introduction
Coherence is a fundamental characteristic of quantum mechanics and a key issue in future devices and information technologies. Measuring coherence is essential to understanding the quantum nature of materials. The coherence of quantum states can be evaluated by measuring interference, such as in Young's double-slit experiment. Irradiating a material with an ultrashort optical pulse can induce both coherent oscillations of interband transition amplitude (polarization) and coherent oscillation of phonons. The former oscillation is referred to as electronic coherence, while the latter is referred to as phonon coherence. In many materials, the coherent oscillation of phonons have been observed using transient reflectivity measurements with single-pulse excitation1,2,3,4,5,6,7,8. Two-pulse excitation, which is used for coherent control technique9,10,11,12,13,14, can be used to measure the interference of electronic and phonon quantum states: When an optical pulse irradiates a material, this creates a coherent superposition of valence band and conduction band states that can be described by a coherent oscillation of the polarization. The second optical pulse enhances or decrease the polarization amplitude from the first pulse via constructive or destructive interference, depending on the relative phases of the two pulses. To measure the relaxation time of the electronic coherence in crystalline GaAs, photon-echo and four-wave-mixing experiments with two-pulse excitation were performed15,16,17,18,19,20,21. The reported relaxation times are in the range from several tens of femtoseconds to a few picoseconds, depending on the sample temperature. However, the electronic and phonon coherence were measured separately, in spite of the correlation between them.
In this study, we simultaneously measured the electronic and phonon coherence in the electron-phonon correlated states induced in bulk solids at room temperature. To accomplish this, we performed transient reflectivity measurements with phase-locked two-pulse excitation, with separation time controlled to sub-femtosecond precision. We examined semiconducting GaAs and semimetallic Bi crystals, whose band gap is near or below the excitation photon energy. In both samples, the transient reflectivity measurements showed coherent oscillations, caused by optical phonons, with relaxation times of a few picoseconds. Interferograms of the amplitudes of the coherent oscillations, obtained by varying the delay of the two pump pulses, showed fringe patterns that represent both the electronic and phonon coherence. The interferometric visibility showed that electronic coherence remained after several tens of femtoseconds in GaAs, while it disappeared within 10 fs in Bi. We discuss the interference using a three-level model for the electron-phonon system and density matrix formalism.
Results
Schematic of the pump-probe reflectivity measurement setup
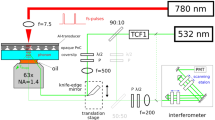
The transient reflectivity was measured with a typical pump-probe technique with electro-optic detection. Figure 1(a) shows a schematic of our pump-probe setup. The output of the Ti:sapphire oscillator (center wavelength = 805 nm (1.54 eV), pulse width = ~50 fs) was split with a partial beam splitter into two beams at a 9:1 ratio; these beams were used as pump and probe pulses, respectively. The pump pulse was introduced into a scan delay unit (APE Scan Delay) to control the delay between the pump and probe pulses. It was then introduced into a Michelson-type interferometer to produce two phase-locked pulses (pulse 1 and 2). The delay (t12) between pulse 1 and 2 was controlled with a precision of ~0.5 fs. The power of pulses 1 and 2 were 40 and 30 mW, respectively. The phase-locked pump pulses were focused on the sample using a lens, which also focused the probe pulse (pulse 3). The beam diameter at the sample position position was measured to be 86 μm (full width of half maximum: FWHM) by the knife-edge method for both pump and probe pulses and fluencies of pulse 1, 2 and 3 was 8.6, 6.5 and 0.2 μJ/cm2/pulse, respectively. The pulse width at the sample position after the lens was estimated to be 60 fs (FWHM) by using the cross-correlation technique with second-harmonic generation. The pump and probe pulse were linearly polarized and the angle between pump and probe polarization was 45 degrees. The reflected pulse from the probe pulse was fed into a polarization beam splitter. The parallel and perpendicular polarized light was monitored with balanced photodiodes (PD1 and PD2). The differential signal from the PDs was amplified with a current amplifier (SRS SR570) and averaged in a digital oscilloscope. The temporal evolution of the reflectivity change (ΔR) was measured by scanning the delay (t13) between the first pump and probe pulses, repetitively, at 20 Hz with a fixed t12. To filter non-oscillatory background in the temporal evolution, a bandpass filter (3–300 kHz) was used to amplify the measurements. The samples were single crystals of n-type GaAs and Bi.
Scheme of the present experiment.
(a) Experimental configuration of the pump-probe reflectivity measurement. CM: chirp mirror, BS: beam splitter, PBS: polarization beam splitter, PD: photo diode, Amp: current amplifier, SM: fiber-coupled spectrometer, POL: polarizer. t12 denotes the delay between the two phase-locked pump pulses and t13 denotes the delay between the first pump pulse and the probe pulse. (b, c) Temporal evolution of reflectivities ΔR(t)/R0 in (b) GaAs and (c) Bi, scanning the pump-probe delay t13 and fixing t12 to 0 fs. The insets show the respective Fourier-transformed spectra for t13 = 0.16 to 4.16 ps (GaAs) and t13 = 0.48 to 4.48 ps (Bi). The peaks at 8.7 and 7.7 THz correspond to the longitudinal optical (LO) phonons and the LO phonon–plasmon coupling oscillations in GaAs. The peak at 2.9 THz corresponds to A1g oscillations in Bi. The red curves are fitted with damping oscillations to the data using eq. (1) and parameters described in the manuscript.
Coherent oscillations caused by phonons
Figure 1(b) shows an example of the time-dependent reflectivity (ΔR(t)/R0) from GaAs, scanning t13 and fixing t12 to ~0 fs; this result shows mode beating. The Fourier-transformed (FT) spectrum, shown in the inset of Fig. 1(b), confirms that two modes were coherently excited at frequencies of 8.7 and 7.7 THz, corresponding respectively to the longitudinal optical (LO) phonons and the LO phonon–plasmon coupling (LOPC) oscillations13. ΔR(t)/R0, shown in Fig. 1(b), is described with a linear combination of two damped harmonic oscillators, corresponding to the LO phonons and the LOPC oscillations:

where A0 is the baseline and Ai, Γi, Ti and δI are the phonon amplitude, relaxation time, oscillation period and initial phase, respectively. By curve fitting, we found the oscillation periods (T1 and T2) and relaxation times (Γi and Γ2) to be 115 fs (8.7 THz) and 1.7 ps for the LO phonons and 130 fs (7.7 THz) and 0.8 ps for the LOPC oscillations, respectively.
Figure 1(c) shows the time-dependent reflectivity from Bi, where one mode is coherently excited at the frequency of 2.9 THz, corresponding to the A1g phonons. By fitting to eq. (1), we found the oscillation period and relaxation time to be T1 = 345 fs (2.9 THz) and Γ1 = 3.6 ps, respectively.
Interference in intensities of coherent oscillations
Figure 2(a–e) shows interferograms of the coherent oscillations, obtained by varying the delay between the pump pulses along with the optical interferogram. Figure 2(a) and 2(d) show the optical interferograms; the intensity of the optical interference between pulses 1 and 2 was obtained using a spectrometer. The beat and envelope of the oscillation (as shown in Fig. 2(a)) correspond to the optical cycle and envelope shape of the pulse, respectively. Figure 2(b), 2(c) and 2(e) show examples of the interferograms of the LO phonons, the LOPC oscillations in GaAs and the A1g phonons in Bi; we obtained these values from the peak intensity of the FT spectrum of the transient reflectivity obtained by scanning t13 (same as Fig. 1(b) and 1(c)), with delay t12 scanned with a time step of ~0.5 fs. We observed fast beating with a period of ~2.7 fs, representing electronic coherence, within 80 fs for the LO phonons and LOPC oscillations in GaAs; we observed this same beating within 50 fs for the A1g phonons in Bi. The envelopes of the signals mainly represent the interference of the coherent oscillations of the phonons induced by the pulse 1 and 2, as discussed in Ref. 13. For example, the intensity of the LO phonons in GaAs (Fig. 2(c)) decreased to zero at a half period (58 fs) by destructive interference and then increased again.
Interferograms of phonons and its interferometric visibility in GaAs and Bi.
(a–e) Temporal evolutions of the (a) intensities of the optical pump pulses, (b) the LO phonon–plasmon coupling oscillations, (c) the longitudinal optical (LO) phonons for GaAs and (d) the optical pump pulses and (e) A1g coherent phonons for Bi; t12 is the delay between the two pump pulses scans. (f, g) Interferometric visibility in the temporal evolution of the intensities of (f) the LO phonons and LO phonon–plasmon coupling oscillations in GaAs and (g) the A1g phonons in Bi. The green curves are fits to Gaussian functions.
We calculated the interferometric visibility (V(t12)) of the fast beating as follows:

where Imax and Imin correspond to the maximum and minimum values of the beat around the delay t12, because the interferometric visibility is a measure of coherence22. Figure 2 (f) and 2(g) show the time-dependent visibility of the optical interference, LO phonons and LOPC oscillations in GaAs (Fig. 2(f)) as well as the A1g phonons in Bi (Fig. 2(g)). The time-dependent visibility of the optical interference fits well to a half-Gaussian function with a width of 25–30 fs, corresponding to half the cross-correlation width of the pulses. In contrast, the visibility of the LO phonons and LOPC oscillations in the GaAs intensities was higher than 0.6 at 60 fs and gradually decreased to less than 0.2 within 80 fs, indicating that electronic coherence remained in GaAs at 80 fs. In contrast, the visibility of the A1g phonons in Bi decreased as the optical interference collapsed.
Three-level model calculations
To understand the interference between the electron-phonon coupled states, we performed calculations using a three-level model and density matrix formalism. We approximated the electron-phonon system as three levels of the zero-phonon state in the electronic ground state |g,0〉 and the zero- and one-phonon states in the electronic excitation states |e,0〉 and |e,1〉. The Hamiltonian is expressed as

where  ,
,  and
and  are the energies of the electronic ground and excited states and the phonon energy, respectively. Using the rotating wave approximation, the interaction with the two pump pulses is given as
are the energies of the electronic ground and excited states and the phonon energy, respectively. Using the rotating wave approximation, the interaction with the two pump pulses is given as

where μ is the transition dipole moment, Ω is the central frequency of the pulse, E(t) is the envelope of the pulse centered at t = 0 and α is the electron-phonon coupling constant. To phenomenologically account for the phase relaxation mechanism, we adopt the stochastic model of Anderson and Kubo23,24, in which the excited state energy εe is assumed to have a random fluctuation part f(t) that obeys the Markoffian–Gaussian process defined by the following two-time correlation function:

where γ is the effective frequency of the random force and D is its amplitude. We neglect the phase relaxation in the phonon part because of its long relaxation time. We also assume that the central frequency of the pulse satisfies the resonance condition 
In the interaction representation, the time evolution of the state is obtained by solving the time-dependent Schrödinger equation to the first order of μ as

where  . Equation (6) represents the correlation between electronic and phonon states. The density matrix ρ(t) at t is given by ρ(t) = |ψ(t)〉〈ψ(t)|. The coherent oscillation of the phonon is generated by the superposition of |e,0〉 and |e,1〉 in the impulsive absorption and is observed as an oscillatory modulation in the reflectivity change ΔR(t), which is proportional to the expectation value of the coordinate of the phonon leading to the change in the electric susceptibility. Therefore, the amplitude of the oscillation [ΔR(t)] in ΔR(t) is proportional to the expectation value of the off-diagonal terms between |e,0〉 and |e,1〉,
. Equation (6) represents the correlation between electronic and phonon states. The density matrix ρ(t) at t is given by ρ(t) = |ψ(t)〉〈ψ(t)|. The coherent oscillation of the phonon is generated by the superposition of |e,0〉 and |e,1〉 in the impulsive absorption and is observed as an oscillatory modulation in the reflectivity change ΔR(t), which is proportional to the expectation value of the coordinate of the phonon leading to the change in the electric susceptibility. Therefore, the amplitude of the oscillation [ΔR(t)] in ΔR(t) is proportional to the expectation value of the off-diagonal terms between |e,0〉 and |e,1〉,

in which  means the average over the stochastic process. The right hand side of eq. (7) can be obtained with eqs. (5) and (6) as follows:
means the average over the stochastic process. The right hand side of eq. (7) can be obtained with eqs. (5) and (6) as follows:

where the memory function  is calculated using the Gaussian property of f(t) as
is calculated using the Gaussian property of f(t) as

This function describes the relaxation of the phase memory, encompassing the non-Markoffian decay  in the early stages (γ|t|≪1) to the Markoffian decay
in the early stages (γ|t|≪1) to the Markoffian decay  over long time-spans (γ|t|≫1).
over long time-spans (γ|t|≫1).
With a short enough pulse width, eq. (8) can be simplified for t far after the passage of the pulse 2, as follows:

where  is the pulse area. The electronic fringe pattern arises from the last term, which is superimposed on the phonon fringe pattern. Figure 3 shows an example of simulations with eq. (10), which qualitatively reproduce the experimental interferograms of the phonons. Although the three-level model seems to be a crude approximation for the band-to-band transitions in semiconductors and semimetals, the effect of the continuous spectra in the final states is partially taken into account as the Gaussian decay of the phase memory. The difference in the estimated value of D (0.03 fs−1 for GaAs, 0.05 fs−1 for Bi) is consistent with the difference of the band structure in both materials. In the analysis we assumed that D is a constant within 100 fs, because the carrier lifetime is much longer. For instance, the thermalizatin of nonequilibrium photo-induced carrier has time constant of ~600 fs25 and minority-carrier lifetime is ~10 ns26.
is the pulse area. The electronic fringe pattern arises from the last term, which is superimposed on the phonon fringe pattern. Figure 3 shows an example of simulations with eq. (10), which qualitatively reproduce the experimental interferograms of the phonons. Although the three-level model seems to be a crude approximation for the band-to-band transitions in semiconductors and semimetals, the effect of the continuous spectra in the final states is partially taken into account as the Gaussian decay of the phase memory. The difference in the estimated value of D (0.03 fs−1 for GaAs, 0.05 fs−1 for Bi) is consistent with the difference of the band structure in both materials. In the analysis we assumed that D is a constant within 100 fs, because the carrier lifetime is much longer. For instance, the thermalizatin of nonequilibrium photo-induced carrier has time constant of ~600 fs25 and minority-carrier lifetime is ~10 ns26.
Simulation of interferograms.
Simulation of interferograms for (a) the LO phonons in GaAs and (b) the A1g phonons in Bi, using eq. (10). For these simulations, (a) Ω/2π = 370 THz, ω/2π = 8.7 THz, D = 0.03 fs−1 and γ = 0.01 fs−1 for GaAs; (b) Ω/2π = 370 THz, ω/2π = 3.0 THz, D = 0.05 fs−1 and γ = 0.01 fs−1 for Bi.
Discussion
We simultaneously measured the electronic and phonon coherence by assessing the interference of the electron-phonon correlated states induced by the two phase-locked optical pulses. The interference visibility in the interferogram of the LO phonons and the LOPC (Fig. 2(f)) shows that the measured coherence in GaAs was longer than that measured from the optical interference. We evaluated how long coherence was maintained by measuring the coherence time (τc), where the interferometric visibility decreases to 0.5. The τc for electronic coherence in GaAs was ~70 fs, while the τc extracted from the optical interferogram was 30 fs. This difference indicates that, in the bulk GaAs at room temperature, the coherence of the optical cycle was transferred to the electronic coherence via interband transitions and the coherence was maintained for ~40 fs. We can qualitatively explain this phenomenon using a three-level model for the electron-phonon coupled states. Our measured memory time of the electronic coherence in the electron-phonon correlated states may be a reasonable value: using four-wave mixing experiments, Wehner et al.16 studied coherent control of electron-phonon scattering in a GaAs crystal at 77 K and found a relaxation time for electronic coherence of 140 fs.
In contrast, we found the τc of the A1g phonon in Bi to be ~40 fs (Fig. 2(g)), indicating that the electronic coherence time in Bi was <10 fs, less than that in GaAs. This difference might be explained by the differing band-gaps of GaAs and Bi: GaAs is a semiconductor with a direct band gap of ~1.44 eV27, while Bi is a semimetal with a small band gap (~15 meV)28. The electronic state excited by the pump pulse (1.54 eV) is close to the band edge in GaAs and is within the conduction band in Bi. Thus, compared with GaAs, many paths exist in Bi for dephasing and electron-electron scattering, a behavior that may not be properly described by the simple three-level model. It may be worthy to discuss limitations of our simple three-level model. This model can be applied for weak- and resonance-excitation conditions but not for strong-excitation conditions, in which phonons are excited in high number states and photo-excited carrier concentrations are high. In addition, it cannot be applied for a thin-film sample, in which the response from its top surface should be significant along with that from a bulk, because the surface states are different from the bulk states.
Note that, in the interferograms of the coherent oscillations of phonons in the measured interference from the transient reflectivity, a fringe pattern appears, caused by both the electronic and phonon coherence. By taking the visibility in the interferogram as a function of the delay-time of the double-pumps, the duration of the coherence can be measured both for the electronic part and the phonon part with the subfemtosecond accuracy. This will open up a possibility to reveal the underlying mechanism of the phase relaxation in various conditions of materials. After the electronic coherence is lost in the materials, the phonon coherence is still observed.
Methods
Data processing
The reflected probe pulse was directed to the polarization beam splitter and the parallel and perpendicular components were detected by two lab-made photodetectors (PD1 and PD2) which use p-i-n photodiodes (Hamamatsu Photonics, S5973-01). The polarization of the probe pulse was optimized in order to balance outputs from two photodiodes. Opposite bias was applied to PD1 and PD2 and the differential signal was amplified by using a current amplifier (SRS SR570) and then transferred to a digital oscilloscope (Iwatsu DS-4354 M) at each pump-probe delay t13 with the fast scan unit. The displacement in this scan unit was proportional to the voltage applied and the voltage was swept sinusoidally at 20 Hz for each scan. The time evolution of the amplified differential signal and the applied voltage were monitored with the oscilloscope. The pump-probe delay t13 was obtained from the voltage data. The data were averaged from 500 scans. The crystal orientation of GaAs was obtained to be (511) by X-ray diffraction.
Optical interference
The output (pulse 1 and 2) from the Michelson-type interferometer was directed to the polarizer and a part of the scattered light from the surface of the polarizer was detected with a fiber-connected spectrometer (Ocean Optics USB4000). The obtained spectrum shows spectral interference of the pulses 1 and 2. The pump optical correlation (shown in Fig. 2(a) and 2(d)) was obtained by plotting the integrated intensity of the spectra between 750 and 850 nm with varying the delay t12 between pulses 1 and 2. This optical correlation was measured at the same time of reflectivity measurement for all measurements and was influenced by fluctuation in laser, temperature and alignment. One optical arm of the interferometer was equipped with a 5-nm feed-back stage.
References
De Silverstri, S. et al. Femtosecond time-resolved measurements of optic phonon dephasing by impulsive stimulated raman scattering in α-perylene crystal from 20 to 300 K. Chem. Phys. Lett. 116, 146–152 (1985).
Cho, G. C., Kutt, W. & Kurz, H. Subpicosecond time-resolved coherent-phonon oscillation in GaAs. Phys. Rev. Lett. 65, 764–766 (1990).
Chang, T. K. et al. Impulsive excitation of coherent phonons observed in reflection in bismuth and antimony. Appl. Phys. Lett. 57, 1004–1006 (1990).
Merlin, R. Generating coherent THz phonons with light pulses. Solid State Commun. 102, 297–220 (1997).
Dekorsy, T., Cho, G. C. & Kurz, H. [Coherent phonons in condensed media] ., Light Scattering in Solids VIII[169–209](Springer, Berlin2000).
Kuznetsov, A. V. & Stanton, C. J. Theory of coherent phonon oscillations in semiconductors. Phys. Rev. Lett. 73, 3243–3246 (1994).
Hase, M., Nakashima, S., Mizoguchi, K., Harima, H. & Sakai, K. Ultrafast decay of coherent plasmon-phonon coupled modes in highly doped GaAs,. Phys. Rev. B 60, 16526–16530 (1999).
Forst, M., & Dekorsy, T. [Coherent phonons in bulk and low-dimensional semiconductors]. Coherent vibrational dynamics [De Silvestri, S., Cerullo, G. & Lanzani, G. (ed.)][129–172] (CRC Press, Boca Raton, 2008).
Weiner, A. M., Leaird, D. E., Wiederrecht, G. P. & Nelson, K. A. Femtosecond pulse sequences used for optical manipulation of molecular motion. Science 247, 1317–1319 (1990).
Hase, M. et al. Optical control of coherent optical phonons in bismuth films. Appl. Phys. Lett. 69, 2474–2476 (1996).
DeCamp, M. F., Reis, D. A., Bucksbaum, P. H. & Merlin, R. Dynamics and coherent control of high-amplitude optical phonons in bismuth. Phys. Rev. B 64, 092301 (2001).
Ohmori, K., Sato, Y., Nikitin, E. E. & Rice, S. A. High-precision molecular wave-packet interferometry with HgAr dimers. Phys. Rev. Lett. 91, 243003 (2003).
Hu, J., Misochko, O. V. & Nakamura, K. G. Delayed formation of coherent LO phonon-plasmon coupled modes in n- and p-type GaAs measured using femtosecond coherent control technique. Phys. Rev. B 86, 235146 (2012).
Katsuki, H. et al. All-optical control and visualization of ultrafast two-dimensional atomic motions in a single crystal of bismuth. Nat. Commun. 4, 2801 (2013).
Heberle, A. P. & Baumberg, J. J. Ultrafast coherent control and destruction of excitations in quantum wells. Phys. Rev. Lett. 75, 2598–2601 (1995).
Wehner, M. U., Uim, M. H. Chemla, D. S. & Wegener, M. Coherent control of electron-LO phonons scattering in bulk GaAs,. Phys. Rev. Lett. 80, 1992–1995 (1998).
Gurioli, M., Bogani, F., Cecheriri, S. & Colocci, M. Coherent vs incoherent emission from semiconductor structures after resonant femtosecond excitation. Phys. Rev. Lett. 78, 3205–3208 (1997).
Wegener, M. Quantum coherence in semiconductors. J. Lumin. 87–89, 20–24 (2000).
Axt, V. M. & Kuhn, T. Femtosecond spectroscopy in semiconductors: a ley to coherences, correlations and quantum kinetics. Rep. Prog. Phys. 67, 433–512 (2004).
Bányai, L. et al. Exciton-KLO-phonon quantum linetics: Evidence of memory effects in bulk GaAs. Phys. Rev. Lett. 75, 2188–2191 (1995).
Hügel, W. A. et al. Photon echoes from semiconductor band-to-band continuum transitions in the regime of coulomb quantum kinetics. Phys. Rev. Lett. 83, 3313–3316 (1999).
Waldermann, F. C. et al. Measuring phonon dephasing with ultrafast pulses using Raman spectral interference. Phys. Rev. B 78, 155201 (2008).
Anderson, P. W. A mathematical model for the narrowing of spectral lines by exchange or motion. J. Phys. Soc. Jpn. 9, 316–339 (1954).
Kubo, R. Note on the stochastic theory of resonance absorption. J. Phys. Soc. Jpn. 9, 935–944 (1954).
Kuhl, J., Gobel, E. O., Pfeiffer, Th. & Joniez, A. Subpicosecond carrier trapping in high-defect-density amorphous Si and GaAs. Appl. Phys. A 34, 105–110 (1984).
Sze, S. M. & Ng Kwok, K. Physics of Semiconductor Devises (John Wiley & Sons, 2007).
Blakemore, J. S. Semiconductig and other major properties of gallium arsenide. J. Appl. Phys. 53, R123–181 (1982).
Bogod, Y. A. & Libinson, A. High-temperature oscillations: Measurement of energy parameters of bismuth band spectrum. Solid State Commun. 96, 609–612 (1995).
Acknowledgements
The authors thank H. Chiba, Y. Okano and K. Ohmori of the Institute of Molecular Science (IMS) as well as H. Katsuki of the Nara Institute of Science and Technology for advice on constructing the Michelson-type interferometer. The authors also thank Y. Shikano of IMS for valuable discussions.
Author information
Authors and Affiliations
Contributions
K.G.N. designed the experiment and S.H. constructed part of the apparatus. K.G.N., Y.K. and S.H. wrote the manuscript. S.H., K.K., K.N. and M.H. performed the experiments and S.H. and K.G.N. analyzed the data. All authors discussed the results. Y.K. created the model and performed the calculations. The project was conceived and supervised by K.G.N.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported license. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Hayashi, S., Kato, K., Norimatsu, K. et al. Measuring quantum coherence in bulk solids using dual phase-locked optical pulses. Sci Rep 4, 4456 (2014). https://doi.org/10.1038/srep04456
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04456
This article is cited by
-
Coherent control theory and experiment of optical phonons in diamond
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.