Abstract
Constructing a discrete model like a cellular automaton is a powerful method for understanding various dynamical systems. However, the relationship between the discrete model and its continuous analogue is, in general, nontrivial. As a quantum-mechanical cellular automaton, a discrete-time quantum walk is defined to include various quantum dynamical behavior. Here we generalize a discrete-time quantum walk on a line into the feed-forward quantum coin model, which depends on the coin state of the previous step. We show that our proposed model has an anomalous slow diffusion characterized by the porous-medium equation, while the conventional discrete-time quantum walk model shows ballistic transport.
Similar content being viewed by others
Introduction
Cellular automata – discrete models that follow a set of rules1 – have been analyzed in various dynamical systems in physics, as well as in computational models and theoretical biology; well-known examples include crystal growth and the Belousov-Zhabotinsky reaction. To simulate quantum mechanical phenomena, Feynman2 proposed a quantum cellular automaton (the Feynman checkerboard). This model, defined in the general case by Meyer3, is known as the discrete-time quantum walk (DTQW). Since the DTQW on a graph is a model of a universal quantum computation4,5, it is of great utility, especially in quantum information6,7,8,9. Furthermore, the DTQW has been demonstrated experimentally in various physical systems10,11,12,13,14,15,16,17,18,19,20,21,22,23,24 to reveal quantum nature under dynamical systems.
As the cellular automaton can be mapped to various differential equations by taking the continuous limit, some DTQW models can be mapped to the Dirac equation25,26,27, the spatially discretized Schrödinger equation28,29, the Klein-Gordon equation27,30, or various other differential equations31,32. These equations have ballistic transport properties, which are reflected mathematically in the one-dimensional (1D) DTQW with a time- and spatial-independent coin operator, i.e. a 1D homogeneous DTQW33. We consider here the 1D DTQW model. Physically, the standard deviation of the homogeneous DTQW is σ(t) ~ t, whereas the unbiased classical random walk has a standard deviation of  .
.
In the homogeneous DTQW, the time evolution of a quantum particle (walker) is given by a unitary operator U defined on the composite Hilbert space  , where
, where  is the walker Hilbert space and
is the walker Hilbert space and  is the two-dimensional coin Hilbert space. For a unitary operator U, the quantum state evolves in each time step t by
is the two-dimensional coin Hilbert space. For a unitary operator U, the quantum state evolves in each time step t by

with

where the upper  (lower
(lower  ) component corresponds to the left (right) coin state at the j-th site at time step t. As an example, the time evolution of the DTQW is given by
) component corresponds to the left (right) coin state at the j-th site at time step t. As an example, the time evolution of the DTQW is given by

The j-th site probability at time step t is given by  and
and  is satisfied for each time step t.
is satisfied for each time step t.
As a generalization of Eq. (3), we define a DTQW with a feed-forward quantum coin described by

with the site-dependent rate function

which incorporates the nearest-neighbor interactions. Since this quantum coin depends on the probability distribution of the coin states on the nearest-neighbor sites at the previous step, this model is called a feed-forward DTQW. It is remarked that the feed-forward DTQW is one of the nonlinear DTQW models. Note that if we set the rate function  to g = cos θ, which is time and site independent, then the model in Eq. (4) reduces to the homogeneous model in Eq. (3). We will show that our proposed feed-forward DTQW is experimentally feasible. Furthermore, we will show that this model shows the anomalous diffusion as introduced below.
to g = cos θ, which is time and site independent, then the model in Eq. (4) reduces to the homogeneous model in Eq. (3). We will show that our proposed feed-forward DTQW is experimentally feasible. Furthermore, we will show that this model shows the anomalous diffusion as introduced below.
One of the famous anomalous diffusion equations is the porous medium equation (PME)34, defined by

where the real parameter m > 1 characterizes the degree of porosity of the porous medium. It is known that the PME can be derived from three physical equations for the density ρ, pressure p and velocity v of the gas flow: the equation of continuity, ∂ρ/∂t + ∇ · (ρv) = 0; Darcy's law, v ∝ −∇p; and the equation of state for a polytropic gas, p ∝ ρν, where ν is the polytropic exponent and m = ν + 1. One of the peculiar features of the PME is the so-called finite propagation, which implies the appearance of a free boundary separating the positive region (p > 0) from the empty region (p = 0).
A well-known solution of the PME is the Barenblatt-Pattle (BP) one35; it is self-similar and its total mass is conserved during evolution. The evolutionary behavior of the BP solution was recently studied in the context of generalized entropies and information geometry36. The BP solution can also be expressed by Tsallis' one-real-parameter (q) generalization of a Gaussian function, i.e., the q-Gaussian37. In the case of 1D space, the BP solution is

with q = 2 − m. Here,  is a positive parameter that characterizes the width of the q-Gaussian at time t and is similar to the variance
is a positive parameter that characterizes the width of the q-Gaussian at time t and is similar to the variance  in a standard Gaussian. In other words, the parameter σq(t) characterizes the spread of the q-Gaussian distribution38,39;
in a standard Gaussian. In other words, the parameter σq(t) characterizes the spread of the q-Gaussian distribution38,39;

which reduces to  in the limit of q → 1. Note that in the same limit, the q-Gaussian reduces to the standard Gaussian,
in the limit of q → 1. Note that in the same limit, the q-Gaussian reduces to the standard Gaussian,  and the PME reduces to the standard heat equation ∂p/∂t = ∂2p/∂x2.
and the PME reduces to the standard heat equation ∂p/∂t = ∂2p/∂x2.
In this paper, we analyze a specific feed-forward DTQW with an experimental proposal using the polarized state and optical mode. We show numerically that the probability distributions of the feed-forward DTQW model have anomalous diffusion characterized by σq= 0.5(t) ~ t0.4. These dynamics are consistent with the time evolution of the self-similar solution35 of the PME, which is known to describe well the anomalous diffusion of an isotropic gas through a porous medium. Furthermore, we show analytically that the interference terms in our model help the speedup of the associated Markovian model but does not help the quadratic speedup like the homogeneous DTQW does40. Note that although anomalous diffusion was found numerically in a nonlinear model41, an aperiodic time-dependent coin model42 and the history-dependent coin43 from the time dependence of the variance σq= 1(t), the partial differential equation (PDE) corresponding to their models have not derived due to the lack of the numerical step (about 100 step). Therefore, we have not yet revealed the origin of the anomalous diffusion in the DTQW.
Results
Experimental proposal of feed-forward DTQW
We propose an optical implementation of the feed-forward DTQW. In the simple optical implementation of the homogeneous DTQW, the walker space uses the spatial mode and the coin space does the polarized state. The shift uses the polarized beam splitter and the quantum coin uses the quarter-wave, half-wave and quarter-wave plates, which can arbitrarily rotate the polarized state in the Poincaré sphere. This was experimentally done in Refs. 10,11,12,16,17,18,19,20,21,22.
Let us construct the feed-forward system of the quantum coin. The detectors put at each path to evaluate the probability distribution of the coin state  and
and  . Since our proposed quantum coin depends on
. Since our proposed quantum coin depends on  and
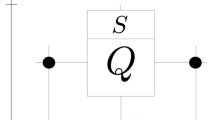
and  , we can calculate the coin operator at the jth site. According to the Jones calculation44 to satisfy Eq. (4), we control the angels of the quarter-wave, half-wave and quarter-wave plates for each path. This can be taken as the quantum coin operator with the feed-forward. This is depicted in Fig. 1. In what follows, we consider the long time time evolution of the feed-forward DTQW.
, we can calculate the coin operator at the jth site. According to the Jones calculation44 to satisfy Eq. (4), we control the angels of the quarter-wave, half-wave and quarter-wave plates for each path. This can be taken as the quantum coin operator with the feed-forward. This is depicted in Fig. 1. In what follows, we consider the long time time evolution of the feed-forward DTQW.
Numerical results of feed-forward DTQW with anomalous diffusion
To study the time evolution of the feed-forward DTQW model, the initial state should have nonzero coin states at the nearest-neighbor sites. This can be easily understood by considering the following example. Let us take ( ,
,  ) as the only non-zero initial state. In this case, the rate is
) as the only non-zero initial state. In this case, the rate is  , because there is no neighboring state. From the map in Eq. (4), we see that the nonzero states at t = 1 are
, because there is no neighboring state. From the map in Eq. (4), we see that the nonzero states at t = 1 are  and
and  . This gives
. This gives  and we see that the only nonzero state is
and we see that the only nonzero state is  at t = 2. This state at t = 2 only differs in sign (or phase) from the initial state. Thus if the initial state is concentrated at a single site, no spreading occurs; the state only oscillates around the initial site.
at t = 2. This state at t = 2 only differs in sign (or phase) from the initial state. Thus if the initial state is concentrated at a single site, no spreading occurs; the state only oscillates around the initial site.
Figure 2 (A) shows a typical probability distribution of the feed-forward DTQW after a long-time evolution. See the Supplementary Movie for more details. The initial state was set as  . We note that the probability distribution diffuses very slowly and does not approach a Gaussian. These features are often observed in anomalous diffusion. It is also remarked that such behavior has not yet seen in DTQWs with the position-dependent coin45,46,47,48, which show the localization property.
. We note that the probability distribution diffuses very slowly and does not approach a Gaussian. These features are often observed in anomalous diffusion. It is also remarked that such behavior has not yet seen in DTQWs with the position-dependent coin45,46,47,48, which show the localization property.
Anomalous slow diffusion of the feed-forward DTQW model.
Its probability distribution at t = 107 step displayed in Panel (A) with running averaged over 10 data sets (light blue line) is fitted by the q-Gaussian (7) with q = 0.5 (red line) to obtain the q-generalized standard deviation σq(t) in Panel (B). Panel (C) shows the long-time evolution of the q-generalized standard deviation σq(t) (green dots), which is well fitted by σq= 0.5(t) ~ t0.4 (red line).
We performed long-time numerical simulations of the feed-forward DTQW model [Eq. (4)] for up to t ~ 108 steps. To study the asymptotic behavior, we take running averages of the numerical solutions to reduce the influence of multiple spikes. The averaged data were fitted with the q-Gaussian of Eq. (7) to determine the corresponding q-generalized standard deviation σq(t), as shown in Fig. 2 (B). We note that the averaged data at each time step are well fitted by the q-Gaussian with q = 0.5.
The long-time evolution of σq(t), plotted in Fig. 2 (C), reveals that the time evolution of the feed-forward DTQW model is well characterized by σq= 0.5(t) ~ t0.4, which is the same time dependency for q = 0.5 of the PME [Eq. (8)].
Analytical derivation of anomalous diffusion in the associated Markov model of feed-forward DTQW
The relationship between our model and the PME can be explored using the decomposition method of Romanelli et al.40,49, in which the unitary evolution of a DTQW model is decomposed into Markovian and interference terms. We obtain the following map for both coin distributions  and
and  :
:

where the two terms including  are interference terms and
are interference terms and  is the real part of a complex number z.
is the real part of a complex number z.
Neglecting the interference terms and introducing the abbreviations  and
and  , we get the associated Markovian model;
, we get the associated Markovian model;


The numerical simulation of the associated Markovian model is performed under initial conditions of  and the typical probability distribution shown in Fig. 3 (A) is well fitted by the q-Gaussian with q = 0.0. Furthermore, Fig. 3 (B) shows that the time evolution of σq(t) of the associated Markovian model is well fitted to σq= 0.0(t) ~ t0.33, which again is the same time dependency as the PME for q = 0.
and the typical probability distribution shown in Fig. 3 (A) is well fitted by the q-Gaussian with q = 0.0. Furthermore, Fig. 3 (B) shows that the time evolution of σq(t) of the associated Markovian model is well fitted to σq= 0.0(t) ~ t0.33, which again is the same time dependency as the PME for q = 0.
Anomalous slow diffusion of the associated Markovian model for the nonlinear quantum walk.
Panel (A) shows the probability distribution of the associated Markovian model at t = 107 step (green dots) fitted by the q-Gaussian, yielding q = 0.0 and σq= 0.0(t) = 283 (red line). Panel (B) shows the long-time evolution of the q-generalized standard deviation σq(t) of the associated Markovian model (blue dots). It is well fitted by σq= 0.0(t) ~ t0.33 (red line).
It is known that the classical Markovian model, i.e. one without the interference terms of the homogeneous DTQW, satisfies the standard heat equation in the continuous limit. Consequently, the associated asymptotic probability distribution is a standard Gaussian. This implies that the ballistic transport property of the homogeneous DTQW comes from the interference term40. We thus consider the continuous limit50 of the associated Markovian model.
We introduce the density ρ(x, t) and current j(x, t) as

where Δx is the difference of the nearest-neighbor sites. Taking a Taylor expansion of Eq. (10), we get

in the diffusion limit, i.e., the quantity (Δx)2/Δt remains constant (set to unity here for simplicity) as Δt, Δx → 0 with the one-step time difference Δt. In a similar manner, by expanding Eq. (11) and taking the diffusion limit, we obtain

which implies a breakdown in Fick's first law (j ∝ −∂ρ/∂x) and is the hallmark of anomalous diffusion. By substituting Eq. (14) into Eq. (13), we obtain the following nonlinear PDE:

Evaluating the asymptotic solution of this nonlinear PDE, after a long-time evolution, ρ(x, t) becomes much less than unity. As the rough approximation in this long-time limit, we have 1 − ρ ≈ 1 and ρ2 ≈ 0 and Eq. (15) is thus well approximated by

which is nothing but the PME in Eq. (6) with m = 2 (q = 0). We thus conclude that the approximated asymptotic solution of Eq. (15) is a q-Gaussian with q = 0. In addition, we can show that this result is mathematically valid by applying the asymptotic Lie symmetry method51 (see Method). This method can give an equivalence between the asymptotic solution of the PDE and the analytically-solved one of the other PDE without analytically solving this PDE. Therefore, the associated Markovian model exhibits anomalous diffusion described by the PME in Eq. (6) with m = 2. This implies that the interference term of our model leads to the speed-up of the quantum walker σq= 0.5 ~ t0.4 compared to the associated Markovian model σq= 0 ~ t1/3 and makes the zig-zag shape around the q-Gaussian distribution.
In summary, we have proposed a feed-forward DTQW model Eq. (4) in which the coin operator depends on the coin states of the nearest-neighbor sites. We show that this model is experimentally feasible. Our feed-forward DTQW model asymptotically satisfies the PME for m = 1.5 (q = 0.5) and exhibits anomalous slow diffusion σq= 0.5(t) ~ t0.4 from the probability distribution and the time dependency of the standard deviation defined in the q-Gaussian distribution.
Discussion
In this section, we show that our results after the long-time numerical simulations have no initial coin dependence and that the interference term can be taken as the noise source in addition to the PME. First, while the above analysis uses the only fixed initial coin states as  , we numerically confirm that there is almost no dependence of the initial coin state except for the trivial cases as follows. We have performed the several numerical simulations for the initial state specified by
, we numerically confirm that there is almost no dependence of the initial coin state except for the trivial cases as follows. We have performed the several numerical simulations for the initial state specified by  and
and  with the real-parameter β and γ ranging from 0 to 1. Note that the trivial cases, β = 0.5, γ = 0 and β = 0, γ = 0.5, lead to the localization of the probability distribution for any time and we cannot define the parameter q for the trivial initial states. Figure 4 shows the numerical evaluation of the parameter q of q-Gaussian distribution from the data at the two different time steps t = 106 and t = 107, under the assumption to satisfy the stationary solution of the PME [Eqs. (7) and (8)]. The evaluated q-parameters for the various initial states are
with the real-parameter β and γ ranging from 0 to 1. Note that the trivial cases, β = 0.5, γ = 0 and β = 0, γ = 0.5, lead to the localization of the probability distribution for any time and we cannot define the parameter q for the trivial initial states. Figure 4 shows the numerical evaluation of the parameter q of q-Gaussian distribution from the data at the two different time steps t = 106 and t = 107, under the assumption to satisfy the stationary solution of the PME [Eqs. (7) and (8)]. The evaluated q-parameters for the various initial states are  except for the trivial cases. Therefore, we can conclude that our nonlinear model shows the anomalous slow diffusion to satisfy the PME with
except for the trivial cases. Therefore, we can conclude that our nonlinear model shows the anomalous slow diffusion to satisfy the PME with  (
( ) without the initial state dependence.
) without the initial state dependence.
Initial coin state dependence.
Changing the parameters β and γ, we numerically evaluate the parameter q of q-Gaussian distribution for 225 different initial states expressed by  and
and  . Note that the trivial cases, β = 0.5, γ = 0 and β = 0.5, γ = 1, are not plotted. Our fitting result except for the trivial cases is
. Note that the trivial cases, β = 0.5, γ = 0 and β = 0.5, γ = 1, are not plotted. Our fitting result except for the trivial cases is  .
.
Finally, let us consider the difference between the probability distribution of our model and the q-Gaussian distribution with q = 0.5, as shown in Fig. 2 (B); the power spectrum of this difference exhibits a white noise as shown in Fig. 5. This power spectrum divided by the physical time scale t0.4 may remain finite in the asymptotic case, which suggests that our nonlinear model may be mapped to the stochastic PME, i.e. the PME plus a white noise term, in the continuous limit. This stochasticity must come from the interference term. The problem of extracting the stochasticity from a deterministic process has been discussed in another context, that of Mori's noise52. Further analysis of this model may reveal the origin of the stochasticity. This is interesting as a purely mathematical problem of a stochastic nonlinear partial differential equation and for showing the relationship between the discrete model and its continuous limit.
The difference between the nonlinear model and the fit.
The power spectrum of the difference between the probability distribution of our model and the q-Gaussian with q = 0.5 at 107 step. To remove the effects of the expectation value, we replace x with x − 36.91 in the q-Gaussian with q = 0.5 [Eq. (7)].
Methods
In what follows, the solution of Eq. (15) is asymptotically identical to the solution of Eq. (16). This is mathematically equivalent to showing that the probability distribution

is invariant under an asymptotic Lie symmetry51 of the nonlinear partial differential equation (15). In other words,

In Eq. (17), Z(σq= 0) = 4σq= 0/3 is the normalization factor and in what follows, the argument of this function is omitted where possible and ∂tρ is denoted as ρt for simplicity.
We follow the asymptotic Lie symmetry method and notations in Ref. 51. Under an infinitesimal transformation with the generator

that is

the function ρ(x, t) is mapped to a new function  , with
, with

By applying this to the probability distribution Eq. (17), we see that the transformation X with ξ = −x leaves Eq. (17) invariant if and only if

Note that τ = η · t remains unrestricted at this stage because ρ(q = 0)(x) does not explicitly depend on time t. Conversely, the function ρ(x) is invariant under  for any τ if and only if ρ(x) is of the form given in Eq. (17).
for any τ if and only if ρ(x) is of the form given in Eq. (17).
Following the general procedure for a Lie group analysis of differential equations53, the second prolongation of X is described by

The coefficients Ψt, Ψx and Ψxx are defined as follows. Under an infinitesimal transformation of X, the partial derivatives are transformed as  ,
,  and
and  . We then readily obtain
. We then readily obtain

The coefficients Ψt, Ψx and Ψxx are then obtained by applying the prolongation formula (2.39) from Ref. 52:



We note that Eq. (18) can be written as

with

The asymptotic Lie symmetry condition

with

can be written in the following compact form:

When the condition in Eq. (30) is fulfilled, each Ak(k = 0, 1, 2, 3) function must vanish separately in the asymptotic limit

implying that the variance σq= 0 also becomes infinity in the asymptotic limit from Eq. (17);

The function A3 can be expressed as

which must be nonzero as σq= 0 → ∞, unless we choose

Making this choice, X becomes

and A3 reduces to

Thus, A3 → 0 as σq= 0 → ∞.
In a similar manner, A0, A1 and A2 are given by

and all become zero as σq= 0 → ∞. Therefore, we conclude that the distribution in Eq. (17) is an invariant solution for the transformation X of Eq. (37), which is an asymptotic symmetry for large |x| of the nonlinear partial differential equation Eq. (18).
References
von Neumann, J. The general and logical theory of automata, in Cerebral Mechanisms in Behavior: The Hixon Symposium Jeffress, L. A. (Ed.), pp. 1–41 (John Wiley and Sons, New York, NY, 1951).
Feynman, R. P. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 20, 367–387 (1948).
Meyer, D. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 85, 551–574 (1996).
Lovett, N. B. et al. Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 81, 042330 (2010).
Childs, A., Gosset, D. & Webb, Z. Universal Computation by Multiparticle Quantum Walk. Science 339, 791–794 (2013).
Kempe, J. Quantum random walks - an introductory overview. Contemp. Phys. 44, 307–327 (2003).
Venegas-Andraca, S. E. Quantum walks: a comprehensive review. Quant. Inf. Proc. 11, 1015–1106 (2012).
Kitagawa, T. Topological phenomena in quantum walks: elementary introduction to the physics of topological phases. Quant. Inf. Proc. 11, 1107–1148 (2012).
Shikano, Y. From Discrete Time Quantum Walk to Continuous Time Quantum Walk in Limit Distribution. J. Comput. Theor. Nanosci. 10, 1558–1570 (2013).
Do, B. et al. Experimental realization of a quantum quincunx by use of linear optical elements. J. Opt. Soc. Am. B 22, 499–504 (2005).
Zhang, P. et al. Demonstration of one-dimensional quantum random walks using orbital angular momentum of photons. Phys. Rev. A 75, 052310 (2007).
Perets, H. B. et al. Realization of Quantum Walks with Negligible Decoherence in Waveguide Lattices. Phys. Rev. Lett. 100, 170506 (2008).
Karski, M. et al. Quantum Walk in Position Space with Single Optically Trapped Atoms. Science 325, 174–177 (2009).
Peruzzo, A. et al. Quantum walks of correlated particles. Science 329, 1500–1503 (2010).
Zähringer, F. et al. Realization of a Quantum Walk with One and Two Trapped Ions. Phys. Rev. Lett. 104, 100503 (2010).
Schreiber, A. et al. Photons Walking the Line: A Quantum Walk with Adjustable Coin Operations. Phys. Rev. Lett. 104, 050502 (2010).
Kitagawa, T. et al. Observation of topologically protected bound states in photonic quantum walks. Nat. Comm. 3, 882 (2012).
Schreiber, A. et al. A 2D Quantum Walk Simulation of Two-Particle Dynamics. Science 336, 55–58 (2012).
Sansoni, L. et al. Two-Particle Bosonic-Fermionic Quantum Walk via Integrated Photonics. Phys. Rev. Lett. 108, 010502 (2012).
Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photon. 7, 322–328 (2013).
Jeong, Y.-C. et al. Experimental realization of a delayed-choice quantum walk. Nat. Comm. 4, 2471 (2013).
Xue, P. et al. Observation of quasiperiodic dynamics in a one-dimensional quantum walk of single photons in space. e-print: arXiv:1312.0123 (2013).
Fukuhara, T. et al. Microscopic observation of magnon bound states and their dynamics. Nature 502, 76–79 (2013).
Manouchehri, K. & Wang, J. Physical Implementation of Quantum Walks (Springer, Berlin, 2014).
Strauch, F. W. Relativistic effects and rigorous limits for discrete- and continuous-time quantum walks. J. Math. Phys. 48, 082102 (2007).
Sato, F. & Katori, M. Dirac equation with an ultraviolet cutoff and a quantum walk. Phys. Rev. A 81, 012314 (2010).
Chandrashekar, C. M., Banerjee, S. & Srikanth, R. Relationship between quantum walks and relativistic quantum mechanics. Phys. Rev. A 81, 062340 (2010).
Chisaki, K., Konno, N., Segawa, E. & Shikano, Y. Crossovers induced by discrete-time quantum walks. Quant. Inf. Comp. 11, 741–760 (2011).
Childs, A. M. On the Relationship Between Continuous- and Discrete-Time Quantum Walk. Comm. Math. Phys. 294, 581–603 (2010).
di Molfetta, G. & Debbasch, F. Discrete time Quantum Walks: continuous limit and symmetries. J. Math. Phys. 53, 123302 (2012).
Knight, P., Roldán, E. & Sipe, J. E. Propagating Quantum Walks: the origin of interference structures. J. Mod. Opt. 51, 1761–1777 (2004).
de Valcarcél, G. J., Roldán, E. & Romanelli, A. Tailoring discrete quantum walk dynamics via extended initial conditions. New J. Phys. 12, 123022 (2010).
Konno, N. Quantum Random Walks in One Dimension. Quant. Inf. Proc. 1, 345–354 (2002); A new type of limit theorems for the one-dimensional quantum random walk. J. Math. Soc. Jpn. 57, 935–1234 (2005).
Vazquez, J. L. The Porous Medium Equation, Mathematical Theory (Oxford University Press, Oxford, 2006).
Barenblatt, G. I. Scaling, Self-Similarity and Intermediate Asymptotics (Cambridge University Press, Cambridge, 1996).
Ohara, A. & Wada, T. Information geometry of q-Gaussian densities and behaviors of solutions to related diffusion equations. J. Phys. A 43, 035002 (2010).
Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World (Springer, New York, NY, 2009).
Anteneodo, C. Non-extensive random walks. Physica A 358, 289–298 (2005).
Schwämmle, V., Nobre, F. D. & Tsallis, C. q-Gaussians in the porous-medium equation: stability and time evolution. Eur. J. Phys. B 66, 537–546 (2008).
Romanelli, A. Distribution of chirality in the quantum walk: Markovian process and entanglement. Phys. Rev. A 81, 062349 (2010).
Navarrete-Benlloch, C., Pérez, A. & Roldán, E. Nonlinear optical Galton board. Phys. Rev. A 75, 062333 (2007).
Ribeiro, P., Milman, P. & Mosseri, R. Aperiodic quantum random walks. Phys. Rev. Lett. 93, 190503 (2004).
Rohde, P. P., Brennen, G. K. & Gilchrist, A. G. Quantum walks with memory provided by recycled coins and a memory of the coin-flip history. Phys. Rev. A 87, 052302 (2013).
Yariv, A. Optical Electronics in Modern Communications (Oxford University Press, Oxford, 1997).
Romanelli, A. The Fibonacci quantum walk and its classical trace map. Physica A 388, 3985–3990 (2009).
McGettrick, M. One Dimensional Quantum Walks with Memory. Quantum Inf. Comp. 10, 0509–0524 (2010).
Joye, A. & Merkli, M. Dynamical Localization of Quantum Walks in Random Environments. J. Stat. Phys. 140, 1–29 (2010).
Shikano, Y. & Katsura, H. Localization and fractality in inhomogeneous quantum walks with self-duality. Phys. Rev. E 82, 031122 (2010); Notes on Inhomogeneous Quantum Walks. AIP Conf. Proc. 1363, 151–154 (2011).
Romanelli, A. et al. Quantum random walk on the line as a Markovian process. Physica A 338, 395–405 (2004).
Godoy, S. & García-Colín, L. S. From the quantum random walk to classical mesoscopic diffusion in crystalline solids. Phys. Rev. E 53, 5779–5785 (1996).
Gaeta, G. Asymptotic symmetries in an optical lattice. Phys. Rev. A 72, 033419 (2005).
Mori, H. Transport, Collective Motion and Brownian Motion. Prog. Theor. Phys. 33, 423–455 (1965); A Continued-Fraction Representation of the Time-Correlation Functions. Prog. Theor. Phys. 34, 399–416 (1965).
Olver, P. J. Applications of Lie Groups to Differential Equations (Springer-Verlag, New York, NY, 1986).
Acknowledgements
Y.S. thanks Masao Hirokawa for valuable discussions. This work was partially supported by the Joint Studies Program of the Institute for Molecular Science.
Author information
Authors and Affiliations
Contributions
Y.S. provided the theoretical model of the discrete-time quantum walk; T.W. and J.H. provided the numerical analysis; and T.W. provided the analytical solution of the associated Markovian model with assistance from Y.S. Y.S. conducted this project. All authors contributed to writing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Probability Distribution of Feed-forward DTQW
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Shikano, Y., Wada, T. & Horikawa, J. Discrete-time quantum walk with feed-forward quantum coin. Sci Rep 4, 4427 (2014). https://doi.org/10.1038/srep04427
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04427
This article is cited by
-
Negative correlations can play a positive role in disordered quantum walks
Scientific Reports (2021)
-
Quantum walk hydrodynamics
Scientific Reports (2019)
-
A nonlinear quantum walk induced by a quantum graph with nonlinear delta potentials
Quantum Information Processing (2019)
-
Weak limit theorem for a nonlinear quantum walk
Quantum Information Processing (2018)
-
Discrete-time quantum walks in random artificial gauge fields
Quantum Studies: Mathematics and Foundations (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.