Abstract
Ion current rectification dependent on the concentration gradient of KCl solutions was systematically investigated in polyethyleneimine modified glass nano-pipettes with inner diameter of 105 nm. Peak shape dependence of the rectification factor on outer KCl solution concentration was observed when inner KCl solution with concentration from 1 mM to 500 mM was used. The peak shape dependence was also observed when the concentrations of the inner and outer KCl solutions were identically controlled. The peak shape in the ion current rectification could be explained by the ion conductance changes through the conical nano-pipette, which result from modulation of ion concentration.
Similar content being viewed by others
Introduction
Glass pipettes have been widely used as a tool for transferring different types of liquids with various volumes1. As going down the size of pipettes to micro or nano-meters, many novel phenomena and applications are involved. For example, the glass pipettes were used to obtain the ionic currents flowing through a cell's plasma membrane in the patch clamp technique2,3. The low volume liquid delivery induced by electric field was realized and used for nano-fluidics and nano-lithography, which were essential for applications to controlled delivery and selective deposition4,5,6,7. Pipettes could be also used as probes in scanning electrochemical microscopy (SECM) and scanning ion conductance microscopy (SICM) for high resolution imaging8,9,10. Moreover, ion transfer process and its kinetic parameters at a liquid/liquid interface were studied using nano-pipettes11.
Ion current rectification (ICR), which was a very important nonlinear ion current-voltage (I-V) behavior in the voltage-gated ion channels, was initially discovered in biological systems12,13. In 1997, ICR using a quartz nano-pipette electrode was discovered by Wei et al.14. Since then, ICR has been observed in various materials and geometries, such as conical silica nano-pores15, ion-track-etched conical polymer membranes16,17, nano-pipettes14,18 and nano-channels19,20. ICR could be also observed in a micro-pore with 2.2 μm diameter21, although it was typically found in nano-sized gaps. The recent progress of building artificial nano-channels which possessed ICR properties was reviewed in detail by Jiang et al.22,23. ICR was generally affected by pore size24, surface charge density25,26, electrolyte concentration14,27, pore geometry28,29 and species of ions30. Some other factors, such as voltage scan rate31,32 and pressure-driven electrolyte flow33, may also influence ICR.
In addition, the forward direction of ICR could be tuned by concentration gradient and surface charge polarity18,34,35. Cheng et al. studied ICR between two ionic solutions with different concentrations and suggested that the phenomenon resulted from the accumulation and depletion of both cations and anions in homogeneous silica nano-channels by calculation based on Possion-Nernst-Planck theory36. Siwy et al. reported the asymmetric diffusion currents through a charged conical nano-pore with a concentration gradient and interpreted the results based on the effect of salt concentration on the thickness of the electrical double layer related to the surface charge and distribution of electric fields37. Jiang et al. investigated a work that experimentally and theoretically study the influence of pH gradient and ion concentration gradient on ionic transport properties inside the nano-channel38. Very recently, Cao et al. discovered that ICR could be inversed by applying the reverse concentration gradient in negatively charged conical nano-pores and attributed it to the cooperation and competition between geometry-induced asymmetric ion transport and diffusive ion flow16. In addition, peak shape dependence of rectification factor on solution concentration was observed using a polyethyleneimine (PEI) modified pipettes with positively charged surface and tip size from 4 nm to 700 nm39. However, by far, systematic study on ICR in a structurally asymmetric bare or coated nano-pipette with different concentration gradients is rarely reported.
In this study, the dependence of ICR in KCl solutions on concentration gradient in PEI-coated glass nano-pipettes was investigated. A peak shape relationship between ICR and concentration was observed in KCl solutions with or without concentration gradient at the PEI-coated or bare glass nano-pipettes. The conductance changes induced by the concentration changes at the pipette tip coupled with the ion transport in the nano-channel were proposed to elucidate the underlying mechanism.
Results
First, the bare pipette (without PEI modification) with an ID of 105 nm was used to measure ICR behavior as reference. Figure 1 shows typical results obtained using 100 mM KCl solution inside pipette and external KCl solutions with various concentrations. As the concentration of external KCl solution increases, the observed ICR behaviors reveal an inversion from upward to downward direction, as shown in Figure 1a, which is consistent with previous reports16,36. Figure 1b shows that R decreases from 1 mM to 50 mM and increases from 50 mM to 2000 mM as the concentration of external KCl solution increases. The minimum rectification factor occurs at 50 mM of external KCl solution.
The thickness of electrical double layer (δ) can be estimated by the following equation41:

where c is the concentration (in mol/L). From this equation, the double layer thickness is about 0.95 nm at the fixed internal concentration of 100 mM. For concentration less than 100 mM of external solution, the diffusive flow direction induced by concentration gradient is toward external solution, which is opposite to the flow direction generated by the conical geometry. Therefore, in the lower concentration (such as 1 mM or 10 mM) of external solution, the concentration gradient rather than conical geometry may dominate the rectification16. At the positive potential, the electric filed pushes the cations toward external solution as concentration gradient resulting in the higher current and thus upward rectification. As concentration of external solution increases, the concentration gradient becomes weaker and even inversed resulting in the downward rectification. Therefore, further increased concentration of external solution generates naturally downward rectification because at the negative potential the cations move into the pipette, which is in the same direction as the concentration gradient. However, as the concentration of external solution becomes higher, the currents generated by applying positive and negative potential show smaller difference leading to less rectification, which is consistent with the previously reported concentration-gradient-dependent ICR in charged conical nano-pores16.
This behavior can be easily expressed by conductance changes at the tip due to the concentration changes36,39,40, as shown in Figure 1c. At the concentration of 1 mM and 10 mM, the conductance at positive bias is larger than that at negative bias so that the rectification is upward. As the concentration of the external solution increases, the conductance at negative bias becomes larger than that at positive bias leading to downward rectification. The conductance difference between negative and positive bias reaches maximum at 50 mM.
Figure 2 shows the I-V relationships of PEI-coated nano-pipettes with various concentrations of both external and internal KCl solutions (all the obtained I-V curves are shown in Figure S1). Figure 2a shows that for the 1 mM internal KCl solution upward rectification appears at lower external KCl solutions and the I-V curve becomes linear and further downward with increase of external KCl concentration. However, when the internal solution concentration is increased to 10–500 mM, the I-V curves show mostly upward rectification, which is enhanced by increasing external solution concentration to achieve a maximum and then suppressed by further increasing the concentration, as shown in Figures 2b–e.
The dependence of rectification on concentration is demonstrated by plotting the rectification factor versus concentration of external KCl solution, as shown in Figure 3. Figures 3b–e indicates that there exists a maximum rectification factor at a specific concentration gradient. Figure 3a shows that the rectification factor continuously decreases as increasing the external solution concentration for the internal solution of 1 mM, which may be due to the lack of experimental data at extremely low concentration of external solution, according to the previous reports24,39,40. Therefore, we can plot the external solution concentration at a peak point as a function of the internal solution concentration, as shown in Figure 3f which confirms that a data point at 1 mM follows the tendency of the curve well.
Dependence of ion current rectification on external KCl solution concentration for PEI-coated nano-pipettes with internal KCl solution concentration of (a) 1 mM, (b) 10 mM, (c) 50 mM, (d) 100 mM and (e) 500 mM. (f) The external KCl solution concentration at which maximum rectification occurs for an internal KCl solution concentration.
The ion current rectification without concentration gradient is also investigated for a PEI coated glass nano-pipette, as shown in Figure 4a. The I-V curves reveal the similar tendency with those in Figures 2b–e: the rectification is enhanced with concentration up to 50 mM; suppressed by further increase of concentration; almost lost at 500 mM. Because the thickness of diffuse double layer is 0.42 nm at 500 mM, the effect of conical geometry on ion flux becomes weak leading to the rectification factor very close to 1. The maximum of rectification occurs at 50 mM, as shown in Figure 4b. The obtained rectification factor higher than 1 implies that the PEI is successfully coated on the surface of glass nano-pipette.
Discussion
In order to explain the observed phenomena, the relationship between conductance and external solution concentration is plotted in Figure 5. The conductance at +1 V is mostly higher than that at −1 V except for the case of higher external solution concentration with internal solution concentration of 1 mM and 500 mM. Therefore, the rectification is almost higher than 1, which is consistent with the results in Figure 3 and previous results39. The difference of conductance between positive and negative bias increases, reaches maximum and decreases sequentially with external solution concentration independent of concentration gradient. The concentration at the maximum difference of conductance is in good agreement with that at the maximum rectification. Therefore, the conductance changes are suitable for explaining the ICR induced in the nano-pipette with or without a concentration gradient. However, the origin of conductance change has not been clearly pointed out.
Dependence of the conductance at ±1 V on the concentration of external KCl solution (a–e) with or (f) without concentration gradient.
The different concentrations of internal KCl solutions are used: (a) 1 mM, (b) 10 mM, (c) 50 mM, (d) 100 mM and (e) 500 mM. (f) Identical internal and external KCl solutions were used with different concentrations ranging from 1 mM to 500 mM.
In fact, the conductance was related to the ion transport in the nano-channel studied by Kovarik et al.24. When the ion moved from tip (small size) to base (large size), i.e. from a high transference number region at and near the tip to a low transference number region within nano-channel, the high conductance state was formed; opposite directional movement of ion resulted in the low conductance state. Figure 6 shows the schematic diagram of the ion flux through a PEI-coated nano-pipette. According to the result obtained by Pu et al.41, the current relations are obtained:


where the subscripts B, n and L designate the parameters in bath, nano-channel and the left side, respectively. By considering that the electrophoretic mobility μCland μK are very similar, the ratios of the current in the nano-channel to that in the bath (at micro-/nano-channel interface) for different ions can be simplified to36:

Similarly, the ion current ratios near right side are:

After combination of above equations and the continuity of the total currents (JB,L = JB,R) at the two ends of the nano-channel, we have:

In our case, for the nano-pipette with inner diameter of d, the fixed charge concentration (f) is36:

where σS is surface charge density, NA is Avogadro's number and the cation/anion ratios (α and β), in Donnan equilibrium, can be expressed as

where CR and CL represent the bulk ion concentrations and the sign of f depends on the polarity of the fixed surface charge in the nano-channel.
The ion current is carried by cations and anions migrating toward cathode and anode, respectively, based on the assumption of their same electrophoretic mobility41. For the internal solution CR = 100 mM (fixed α), the current ratios in equations (4– 6) with respect to different concentration of external solution CL are plotted in Figure 7 for PEI-coated and bare glass nano-pipettes (the current ratios for variously different CR are shown in Figure S2).  and
and  decrease and
decrease and  and
and  increase as the concentration CL increases. The ratios of
increase as the concentration CL increases. The ratios of  and
and  reach 1 and current equilibrium is achieved at high CL (Figure 7a). The ratios of
reach 1 and current equilibrium is achieved at high CL (Figure 7a). The ratios of  and
and  pass through 1 and are inversed as CL increases (Figure 7b). The cation current ratios calculated for a PEI-coated nano-pipette are identical to the anion current ratios calculated for a bare glass nano-pipette Therefore, the unbalanced flow of ions results in the accumulation and depletion of both K+ and Cl− ions in the nano-pipette and consequently increase and decrease the conductance by applying forward and reverse bias leading to the rectification behaviors36. Figures 7a and b reveals that the ratios of the current in the PEI-coated nano-channel to that in the bath are decreased and increased to 1 for Cl− and K+, respectively. At lower concentration, we have
pass through 1 and are inversed as CL increases (Figure 7b). The cation current ratios calculated for a PEI-coated nano-pipette are identical to the anion current ratios calculated for a bare glass nano-pipette Therefore, the unbalanced flow of ions results in the accumulation and depletion of both K+ and Cl− ions in the nano-pipette and consequently increase and decrease the conductance by applying forward and reverse bias leading to the rectification behaviors36. Figures 7a and b reveals that the ratios of the current in the PEI-coated nano-channel to that in the bath are decreased and increased to 1 for Cl− and K+, respectively. At lower concentration, we have  and
and  . When the positive bias is applied as shown in Figure 6, the ions are accumulated in the nano-channel because ions dragged into the channel are more than those taken out, resulting in the high conduction based on the Poisson-Nernst-Planck equation36,42. On the contrary, when applying the negative bias, the ions are depleted in the nano-channel resulting in low conductance. Therefore, the rectification factors are larger than 1 in this case and it increases with the concentration of external solution because the total accumulated ions increases with the KCl concentration. At the same time, the ratio of
. When the positive bias is applied as shown in Figure 6, the ions are accumulated in the nano-channel because ions dragged into the channel are more than those taken out, resulting in the high conduction based on the Poisson-Nernst-Planck equation36,42. On the contrary, when applying the negative bias, the ions are depleted in the nano-channel resulting in low conductance. Therefore, the rectification factors are larger than 1 in this case and it increases with the concentration of external solution because the total accumulated ions increases with the KCl concentration. At the same time, the ratio of  and
and  decreases, as shown in Figure 7c, which means that the accumulation rate decreases for both cations and anions, therefore, the accumulation should have the maximum corresponding to the maximum rectification. The maximum rectification occurs when the ratio of
decreases, as shown in Figure 7c, which means that the accumulation rate decreases for both cations and anions, therefore, the accumulation should have the maximum corresponding to the maximum rectification. The maximum rectification occurs when the ratio of  and
and  just becomes very close to each other and nearly independent of concentration, as shown in Figure 7c, which means that αβ is very close to 1 from equation (6).
just becomes very close to each other and nearly independent of concentration, as shown in Figure 7c, which means that αβ is very close to 1 from equation (6).
At high concentration, the ratios are  and
and  but very close to 1, which means that the ions moving out are almost balanced with those moving in and thus, the conductance at positive and negative biases are very similar resulting in the less rectifying effect. However, the conductance in this situation is very high leading to high current level, as shown in Figure 2.
but very close to 1, which means that the ions moving out are almost balanced with those moving in and thus, the conductance at positive and negative biases are very similar resulting in the less rectifying effect. However, the conductance in this situation is very high leading to high current level, as shown in Figure 2.
Here, the values of α and β are related to fixed charge concentration f (surface charge density) and bulk concentration CR and CL. However, the current change tendency would be only related to the surface charge polarity and bulk concentration (see Figure S3). Moreover, the surface charge density chosen to be 4.5 mC/m2 is reasonable from αβ → 1 when the maximum occurs, which is in the range of reported data17,36,43, although the real density may be larger than this value. Similarly to the results reported by Cheng et al.36,42, the concentration gradient should result in change of the current ratios and ion conductance while changing external solution concentration.
Finally, we would like to point out that there is a difference between our results, as shown in Figure 8 and the previous report in the concentration-gradient-dependent ion current rectification with fixed 1 mM KCl solution16. From Figure 8a, the diffusive ion flow is toward external solution which is opposite to the ion flux direction induced by the geometry. Thus the rectification factor decreases as the increase of internal solution concentration which is consistent with the previous results16. From Figure 8b, the direction of diffusive ion flow is the same as that induced by geometry which should generate larger rectification factor as increasing the external solution concentration, however, the observed rectification factor still decreases as the increase of external concentration. This could be explained by the conductance changes as shown in insets of Figure 8. As we know, the anions are dominant in a nano-pipette with the positively charged surface33. Combined with Figure S2a, the anion flux inside the nano-pipette is larger than external solution whereas the cation flux is opposite, therefore, the anions accumulated in the nano-pipette when the positive bias applied. For negative bias, the anions deplete in the nano-pipette and thus the conductance at +1 V is always higher than that at −1 V independent of concentration gradient. And it is expected that the higher the concentration is the higher conductance is obtained. As the concentration increases, the ratio of  and
and  is getting close to 1 which means that the ion flux inside the nano-pipette is close to outside of nano-pipette resulting in the smaller difference in conductance by applying positive and negative bias. In summary, the conductance difference at ±1 V becomes smaller as the concentration increases resulting in the smaller rectification factor.
is getting close to 1 which means that the ion flux inside the nano-pipette is close to outside of nano-pipette resulting in the smaller difference in conductance by applying positive and negative bias. In summary, the conductance difference at ±1 V becomes smaller as the concentration increases resulting in the smaller rectification factor.
In conclusion, the surface of glass nano-pipette was successfully modified with PEI by a simple method. The ion current rectification was investigated in the KCl solution with a different concentration gradient. The peak shape dependence of rectification factor on KCl concentration was observed with a wide range of internal KCl concentration (from 1 mM to 500 mM), even in the bare glass nano-pipette. The dependence of rectification on KCl concentration could be explained by ion conductance changes in the nano-pipette with asymmetric geometry, which are caused by modulation of ion concentration.
Methods
The pipettes with inner diameters of ca. 105 nm, as shown in Figure 9a, were fabricated by a CO2-laser-based pipette puller (Model P-2000, Sutter Instrument) with glass capillaries (outer diameter (OD) of 1 mm, inner diameter (ID) of 0.6 mm and length (L) of 9 cm, Narishige group). The program used for fabricating pipettes was shown in the following:


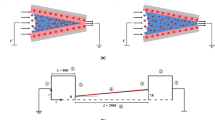
(a) Top view scanning electron microscope (SEM) image of the nano-pipette used in this work and (b) schematic diagram of the experimental set-up. RE, CE and WE denote saturated silver chloride (Ag–AgCl) reference electrode, 0.2 mm diameter Pt wire counter electrode and 0.1 mm diameter Ag wire working electrode, respectively. KCl solutions with different concentrations are filled for current–voltage (I-V) measurement.
The surface charge polarity of glass nano-pipetts were modified using the similar method reported by Shao et al.39. Briefly, 0.1 g PEI (branched, M.W. 25000, CAS 9002-98-6, Sigma-Aldrich) was dissolved in 100 mL distilled water to form 0.1% PEI aqueous solution. First, 0.6 μL of 0.1% PEI aqueous solution was backfilled into the tip of pipette. Then we used centrifugation to drive out the air bubbles, checked it under a microscope (BM1350, Azzota) and placed it in air for 90 minutes to let PEI interact with the inner wall of the pipette. Finally, the pipette was baked at 120°C for more than 2 hours to remove water. The hydrodynamic radius Rh could be evaluated to be about 5.3 nm39. KCl aqueous solutions with different concentrations were injected into pipettes. Then, we used centrifugation and checked it under the microscope to make sure that there were no residual air bubbles in the pipettes and placed it in the external solutions with different concentrations for experiments.
I-V curves were obtained with an electrochemical workstation (VersaSTAT 4, Princeton Applied Research) by changing the voltage from −1 V to +1 V with the step of 25 mV and scan rate of 25 mV/s. A three-electrode system composed of a saturated Ag/AgCl reference electrode and a 0.2 mm diameter Pt wire electrode, which were placed in external solution and a 0.1 mm diameter Ag electrode inserted inside a pipette, was used to investigate the local I-V properties through a nano-pipette, as schematically shown in Figure 9b, which was similar to a previous report44. The I-V curves were measured at least three times using the nano-pipettes with the same size. The rectification factor was defined as R = |I (+1 V)/I(−1 V)| where the current values were determined from the measured I-V curve and the ratio G = I (V)/V at the voltage (V) of ± 1 V was used to define the voltage-dependent conductance of the nano-pipette40.
References
Morris, C. A., Friedman, A. K. & Baker, L. A. Applications of nanopipettes in the analytical sciences. Analyst 135, 2190–2202 (2010).
Zhao, Y. et al. Patch clamp technique: review of the current state of the art and potential contributions from nanoengineering. Proc. IMechE, Part N: J. Nanoengineering and Nanosystems 222, 1–11 (2008).
Malboubi, M., Gu, Y. & Jiang, K. Experimental and simulation study of the effect of pipette roughness on giga-seal formation in patch clamping. Microelectron. Eng. 87, 778–781 (2010).
An, S. M. et al. Low-volume liquid delivery and nanolithography using a nanopipette combined with a quartz tuning fork-atomic force microscope. Nanoscale 4, 6493–6500 (2012).
Suryavanshi, A. P. & Yu, M. F. Probe-based electrochemical fabrication of freestanding Cu nanowire array. Appl. Phys. Lett. 88, 083103 (2006).
Suryavanshi, A. P. & Yu, M. F. Electrochemical fountain pen nanofabrication of vertically grown platinum nanowires. Nanotechnology 18, 105305 (2007).
Laforge, F. O., Carpino, J., Rotenberg, S. A. & Mirkin, M. V. Electrochemical attosyringe. Proc. Natl. Acad. Sci. USA 104, 11895 (2007).
Prater, C. B., Hansma, P. K., Tortonese, M. & Quate, C. F. Improved scanning ion-conductance microscope using microfabricated probes. Rev. Sci. Instrum. 62, 2634 (1991).
Takahashi, Y. et al. Simultaneous Noncontact Topography and Electrochemical Imaging by SECM/SICM Featuring Ion Current Feedback Regulation. J. Am. Chem. Soc. 132, 10118–10126 (2010).
Elsamadisi, P., Wang, Y. X., Velmurugan, J. & Mirkin, M. V. Polished Nanopipets: New Probes for High-Resolution Scanning Electrochemical Microscopy. Anal. Chem. 83, 671–673 (2011).
Li, Q. et al. Fast Ion-Transfer Processes at Nanoscopic Liquid/Liquid Interfaces. Angew. Chem. 121, 8154–8157 (2009).
Schroeder, J. I., Raschke, K. & Neher, E. Voltage dependence of K+ channels in guard-cell protoplasts. Proc. Nati. Acad. Sci. USA 84, 4108–4112 (1987).
Schroeder, J. I. K+ transport properties of K+ channels in the plasma membrane of Vicia faba guard cells. J. Gen. Physiol. 92, 667–683 (1988).
Wei, C., Bard, A. J. & Feldberg, S. W. Current rectification at quartz nanopipet electrodes. Anal. Chem. 69, 4627–4633 (1997).
Cruz-Chu, E. R., Aksimentiev, A. & Schulten, K. Ionic current rectification through silica nanopores. J. Phys. Chem. C. Nanomater Interfaces 113, 1850 (2009).
Cao, L. X., Guo, W., Wang, Y. G. & Jiang, L. Concentration-gradient-dependent ion current rectification in charged conical nanopores. Langmuir 28, 2194–2199 (2012).
Ali, M. et al. Layer-by-layer assembly of polyelectrolytes into ionic current rectifying solid-state nanopores: insights from theory and experiment. J. Am. Chem. Soc. 132, 8338–8348 (2010).
Umehara, S. et al. Current rectification with poly-l-lysine-coated quartz nanopipettes. Nano Lett. 6, 2486–2492 (2006).
Karnik, R., Duan, C. H., Castelino, K., Daiguji, H. & Majumdar, A. Rectification of ionic current in a nanofluidic diode. Nano Lett. 7, 547–551 (2007).
Yeh, L. H., Zhang, M. K., Qian, S. Z., Hsu, J. P. & Tseng, S. J. Ion concentration polarization in polyelectrolyte-modified nanopores. J. Phys. Chem. C 116, 8672–8677 (2012).
Yusko, E. C., An, R. & Mayer, M. Electroosmotic flow can generate ion current rectification in nano- and micropores. ACS Nano 4, 477–487 (2010).
Guo, W., Tian, Y. & Jiang, L. Asymmetric ion transport through ion-channel-mimetic solid-state nanopores. Accounts Chem. Res. 46, 2834–2846 (2013).
Zhang, H. C., Tian, Y. & Jiang, L. From symmetric to asymmetric design of bio-inspired smart single nanochannels. Chem. Commun. 49, 10048–10063 (2013).
Kovarik, M. L., Zhou, K. M. & Jacobson, S. C. Effect of conical nanopore diameter on ion current rectification. J. Phys. Chem. B 113, 15960–15966 (2009).
Liu, J. et al. Surface charge density determination of single conical nanopores based on normalized ion current rectification. Langmuir 28, 1588–1595 (2012).
Siwy, Z., Heins, E., Harrell, C. C., Kohli, P. & Martin, C. R. Conical-nanotube ion-current rectifiers: the role of surface charge. J. Am. Chem. Soc. 126, 10850–10851 (2004).
Siwy, Z. et al. Preparation of synthetic nanopores with transportproperties analogous to biological channels. Surf. Sci. 532–535, 1061–1066 (2003).
Apel, P. Y., Blonskaya, I. V., Orelovitch, O. L., Ramirez, P. & Sartowska, B. A. Effect of nanopore geometry on ion current rectification. Nanotechnology 22, 175302 (2011).
Kubeil, C. & Bund, A. The role of nanopore geometry for the rectification of ionic currents. J. Phys. Chem. C 115, 7866–7873 (2011).
Bhattacharya, S. et al. Rectification of the current in α-Hemolysin pore depends on the cation type: the alkali series probed by molecular dynamics simulations and experiments. J. Phys. Chem. C 115, 4255–4264 (2011).
Guerrette, J. P. & Zhang, B. Scan-rate-dependent current rectification of cone-shaped silica nanopores in quartz nanopipettes. J. Am. Chem. Soc. 132, 17088–17091 (2010).
Momotenko, D. & Girault, H. H. Scan-rate-dependent ion current rectification and rectification inversion in charged conical nanopores. J. Am. Chem. Soc. 133, 14496–14499 (2011).
Lan, W. J., Holden, D. A. & White, H. S. Pressure-dependent ion current rectification in conical-shaped glass nanopores. J. Am. Chem. Soc. 133, 13300–13303 (2011).
Yameen, B. et al. Single conical nanopores displaying pH-tunable rectifying characteristics. Manipulating ionic transport with zwitterionic polymer brushes. J. Am. Chem. Soc. 131, 2070–2071 (2009).
Ali, M., Schiedt, B., Healy, K., Neumann, R. & Ensinger, W. Modifying the surface charge of single track-etched conical nanopores in polyimide. Nanotechnology 19, 085713 (2008).
Cheng, L. J. & Guo, L. J. Rectified ion transport through concentration gradient in homogeneous silica nanochannels. Nano Lettt. 7, 3165–3171 (2007).
Siwy, Z., Kosińska, I. D., Fuliński, A. & Martin, C. R. Asymmetric diffusion through asymmetric nanopores. Phys. Rev. Lett. 94, 048102 (2005).
Zhang, H. C. et al. Bioinspired artificial single ion pump. J. Am. Chem. Soc. 135, 16102–16110 (2013).
Liu, S. J. et al. Studies of Ionic Current Rectification Using Polyethyleneimines Coated Glass Nanopipettes. Anal. Chem. 84, 5565–5573 (2012).
White, H. S. & Bund, A. Ion current rectification at nanopores in glass membranes. Langmuir 24, 2212–2218 (2008).
Pu, Q. S., Yun, J. S., Temkin, H. & Liu, S. R. Ion-enrichment and ion-depletion effect of nanochannel structures. Nano Lett. 4, 1099–1103 (2004).
Cheng, L. J. Ion and Molecule Transport in Nanochannels [dissertation]. Ann Arbor (MI), University of Michigan (2008). (last accessed on 16 Jan. 2014). URL http://hdl.handle.net/2027.42/60830.
Behrens, S. H. & Grier, D. G. The charge of glass and silica surfaces. J. Chem. Phys. 115, 6716–6721 (2001).
Chen, C. C., Zhou, Y. & Baker, L. A. Single-nanopore investigations with ion conductance microscopy. ACS Nano 5, 8404–8411 (2011).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Korea government (MSIP) (No. 2013R1A3A2042120, 2011-0030228 and 2008-0061893 (QMMRC)).
Author information
Authors and Affiliations
Contributions
X.L.D., T.T. and B.H.P. planned the projects; X.L.D., T.T., T.K. and B.H.P. designed the experiments; X.L.D. and E.J.K. made nano-pipettes; X.L.D. and J.W.S carried out ion current measurements; X.L.D. and T.T. performed theoretical analysis; X.L.D., T.T., T.K. and B.H.P. interpreted the results; all authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supporting Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Deng, X., Takami, T., Son, J. et al. Effect of concentration gradient on ionic current rectification in polyethyleneimine modified glass nano-pipettes. Sci Rep 4, 4005 (2014). https://doi.org/10.1038/srep04005
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04005
This article is cited by
-
Nanopore extended field-effect transistor for selective single-molecule biosensing
Nature Communications (2017)
-
Recent advances of DNA sequencing via nanopore-based technologies
Science Bulletin (2015)
-
Nanopipette exploring nanoworld
Nano Convergence (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.