Abstract
In most social and information systems the activity of agents generates rapidly evolving time-varying networks. The temporal variation in networks' connectivity patterns and the ongoing dynamic processes are usually coupled in ways that still challenge our mathematical or computational modelling. Here we analyse a mobile call dataset and find a simple statistical law that characterize the temporal evolution of users' egocentric networks. We encode this observation in a reinforcement process defining a time-varying network model that exhibits the emergence of strong and weak ties. We study the effect of time-varying and heterogeneous interactions on the classic rumour spreading model in both synthetic and real-world networks. We observe that strong ties severely inhibit information diffusion by confining the spreading process among agents with recurrent communication patterns. This provides the counterintuitive evidence that strong ties may have a negative role in the spreading of information across networks.
Similar content being viewed by others
Introduction
In the last ten years the access to high resolution datasets from mobile devices, communication and pervasive technologies has propelled a wealth of developments in the analysis of large-scale networks1,2,3,4. A specific effort has been devoted to characterize how network's structure influences the behaviour of dynamical processes evolving on top of them, an extremely important question for the understanding and modelling of the spreading of ideas, diseases, informations and many others dynamical phenomena5,6,7,8,9. However, the large majority of approaches put forth so far uses a time-aggregated representation of network's interactions, neglecting the time-varying nature of real systems connectivity patterns. This approximation is extremely convenient for the sake of mathematical and computational analysis, but it is prone to introduce strong biases in the description of the dynamical processes occurring on the network2,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28. Indeed, the concurrency and time ordering of interactions are crucial in a correct description of network's processes11,23,29,30,31,32.
The characterization and modelling of time-varying networks are still open and active areas of research33,34. In this context, relational event-based network analysis enable to model network dependent, time-stamped event data3 as well as human and organizational interactions35,36. Appropriate dyadic level statistics govern the rate at which actors send out communications to their neighbours encoding traditional network structures as well as actor level attributes or even the history of actor level events for the sender. A simplification of this framework has been recently proposed by the activity-driven generative algorithm for time-varying networks23. This approach is based on the activity potential, a time invariant function characterizing agents' interactions. This class of models generates activity-driven networks that provides a simplified picture of highly dynamical networks23,24,25,26. The activity-driven framework has considered only memoryless generative processes so far. At each time step, nodes select their partners with a uniform probability. The model thus neglects the heterogeneous nature of individuals' social interactions. Indeed, in real social systems, agents have strong ties defined as connections that are frequently repeated and weak ties signalling occasional interactions. The heterogeneity of social ties is a key ingredient of social networks and plays a crucial role on diffusion processes37. However, a full understanding of the mechanism driving their formation and their effects on dynamical phenomena, explicitly considering the network's time-varying nature, is still missing.
In this paper we propose an extension of the activity-driven framework to model and capture the emergence of heterogeneous ties in social networks. We perform a thorough analysis of a large-scale mobile phone-call (MPC) dataset containing time-stamped communication events of more than six million individuals (for detailed description see Methods). In this system, the interaction dynamics of a node (ego) can be explained by introducing simple memory effects encoded in a non-Markovian reinforcement process. The introduction of this mechanism in the activity-driven model allows capturing the evolution of the egocentric network of each actor in the system. Within this new framework we study a family of information propagation processes, namely the rumour spreading model38,39. We tackle the case in which the dynamics of contacts and the spreading process are acting on the same time-scale. Interestingly, both in synthetic and real time-varying networks we find that memory hampers the rumour spreading process. Strong ties have an important role in the early cessation of the rumor diffusion by favouring interactions among agents already aware of the gossip. The celebrated Granovetter conjecture that spreading is mostly supported by weak ties40, goes along with a negative effect of strong ties. In other words, while favouring locally the rumor spreading, strong ties have an active role in confining the process for a time sufficient to its cessation.
Results
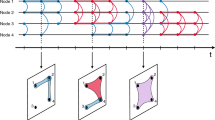
We focus on a prototypical large scale communication network where mobile phone users are nodes and the calls among them links. The common analysis framework for such systems neglects the temporal nature of the connections in favour of time-aggregated representations. In these representations, the degree k of a node indicates the total number of contacted individuals, while the weight of a link w (the strength of the tie) the total number of calls between the pair of connected nodes. The distributions of these quantities are shown in Fig. 1.a and b. Interestingly, they are characterized by heavy-tailed distributions. Although, the study of the time-aggregated network provides basic information about its structure, it cannot inform us on the processes driving its dynamics. This intuition is clearly exemplified in Fig. 2.a and b. These figures show two snapshots of the network at different times covering few hours of calls in a town. The two plots capture dynamical interaction patterns not visible from the aggregated network representation (Fig. 2.c).
Distributions of the characteristic measures of the aggregated MPC network and activity-driven networks.
In panels (a) and (d) we plot the degree distributions. In panels (b) and (e) we plot the weight distributions. Finally, in panels (c) and (f) we plot the activity distributions. In each figure grey symbols are assigning the original distributions while coloured symbols are denoting the same distributions after logarithmic binning. Measured quantities in MPC sequences were recorded for 182 days (see Methods). In panels (d), (e) and (f) solid lines are assigned to the distributions induced by the reinforced process, while dashed lines denote results of the original memoryless process. Model calculations were performed with parameters N = 106,  = 10−4 and T = 104.
= 10−4 and T = 104.
Dynamics of the MPC network.
Panels (a) and (b) show calls within 3 hours between people in the same town in two different time windows. Panel (c) presents the total weighted social network structure, which was recorded by aggregating interactions during 6 months. Node size and colors describe the activity of users, while link width and color represent weight.
Here we aim to study and identify the mechanisms driving the evolution and dynamics of the egocentric networks (egonets) of the global network. Egonets were thoroughly investigated earlier in psychology and sociology41,42,43. Some other characteristics have been recently mapped out with the availability of large-scale data44,45,46,47,48. We tackle this problem from a different angle focusing on the activity rate, a, that allows describing the network evolution beyond simple static measures. It is defined as the probability of any given node to be involved in an interaction at each unit time. The activity distribution is also heavy-tailed (see Fig. 1.c), but contrary to degree and weight, is a time invariant property of individuals23. It does not change by using different time aggregation scales23,25. This quantity is the basic ingredient of the activity-driven modelling framework23. Here we extend this approach by identifying and modelling another crucial component: the memory of each agent. We encode this ingredient in a simple non-Markovian reinforcing mechanism that allows to reproduce with great accuracy the empirical data.
Egocentric network dynamics
In general, social networks are characterized by two types of links. The first class describes strong ties that identify time repeated and frequent interactions among specific couples of agents. The second class characterizes weak ties among agents that are activated only occasionally. It is natural to assume that strong ties are the first to appear in the system, while weak ties are incrementally added to the egonet of each agent1. This intuition has been recently confirmed49 in a large-scale dataset and indicates a particular egocentric network evolution. In order to quantify it, we measure the probability, p(n), that the next communication event of an agent having n social ties will occur via the establishment of a new (n + 1)th link. We calculate these probabilities in the MPC dataset averaging them for users with the same degree k at the end of the observation time. We therefore measure the quantity pk(n) for the egonets with the same degree k and n ≤ k. The empirical pk(n) functions for different degree groups are shown in Fig. 3 inset (coloured symbols). Interestingly, the probabilities are decreasing with n for each degree class denoting a slow down in the egocentric network evolution. The larger the egocentric network, the smaller the probability that the next communication will be with someone who was not contacted before. Agents have memory. They remember their social ties and tend to repeat interactions on these already established connections.
The pk(n) probability functions calculated for different degree groups in the MPC network.
In the inset, symbols show the averaged pk(n) for groups of nodes with degrees between the corresponding  values. Continuous lines are the fitted functions of Eq.1 with c parameter values showed in the legend. The main panel depicts the same functions after rescaling them using Eq.2. The continuous line describes the analytical curve of Eq.2.
values. Continuous lines are the fitted functions of Eq.1 with c parameter values showed in the legend. The main panel depicts the same functions after rescaling them using Eq.2. The continuous line describes the analytical curve of Eq.2.
The empirical growth of the egonet can be captured by a simple mechanism. We find that the probability that a node, characterized by a social circle of size n, will establish a new tie is well fitted by the expression:

Analogously, the probability of having an interaction with someone who is already in the egocentric network is n/(n + c). Here c is an offset constant depending on the degree class considered. By fitting the function in Eq. 1 on the empirical data (solid lines in Fig. 3 inset) we can determine the corresponding constant c for each degree group (see Supplementary Materials (SM) for the obtained values). Using the measured c values we can rescale the empirical pk(n) functions as

and collapse the data points of different degree groups on a single curve (see Fig. 3 main panel). This remarkable result suggests that the same mechanism is driving the evolution of the egonets of all individuals independently of their final number of connections.
Activity-driven network model with memory
The basic activity-driven network model23 considers N nodes, each one assigned with an activity probability per unit time ai = ηxi. Here xi denotes the activity potential drawn from a desired F(xi) distribution ( fixes the minimal value of activity in the system) and η is a rescaling factor that fixes the average number of active nodes per unit time to η〈x〉N. The generative network process is defined according to the following rules: i) At each discrete time step t the network Gt starts with N disconnected vertices; ii) With probability aiΔt each vertex i becomes active and generates m links that are connected to m other randomly selected vertices; iii) At the next time step t + Δt, all the edges in the network Gt are deleted. In this formulation inactive nodes can receive connections. Different rules can be easily implemented to model different scenarios50. Without loss of generality we fix the parameters η = 1,
fixes the minimal value of activity in the system) and η is a rescaling factor that fixes the average number of active nodes per unit time to η〈x〉N. The generative network process is defined according to the following rules: i) At each discrete time step t the network Gt starts with N disconnected vertices; ii) With probability aiΔt each vertex i becomes active and generates m links that are connected to m other randomly selected vertices; iii) At the next time step t + Δt, all the edges in the network Gt are deleted. In this formulation inactive nodes can receive connections. Different rules can be easily implemented to model different scenarios50. Without loss of generality we fix the parameters η = 1,  and Δt = 1. Furthermore, in order to suit the MPC dataset we set m = 1, i.e. each call take place between two people. We consider heavy-tailed distributions of activity i.e. F(x) ∝ x−ν, that reproduce the behaviour observed in real data for a number of real-world networks23,25,51,52. Inspired by measurements in the MPC dataset we set the exponent to ν = 2.8 (see Fig. 1.c and f).
and Δt = 1. Furthermore, in order to suit the MPC dataset we set m = 1, i.e. each call take place between two people. We consider heavy-tailed distributions of activity i.e. F(x) ∝ x−ν, that reproduce the behaviour observed in real data for a number of real-world networks23,25,51,52. Inspired by measurements in the MPC dataset we set the exponent to ν = 2.8 (see Fig. 1.c and f).
In the basic activity-driven model the network dynamics is memoryless (ML). At each time step all connections previously established are removed and the new one are created with no memory of the past. Here we extend the modelling framework introducing a simple reinforcement process in which nodes keep remembering who they have connected46,53,54. Inspired by the observations in the MPC dataset, we impose a reinforcement mechanism in which an active node with n previously established social ties will contact randomly a new node with probability p(n) = c/(n + c). Otherwise, with probability 1 − p(n) = n/(n + c) it will interact with a node already contacted, thus reinforcing earlier established social ties. In this case, the selection is done randomly among the n neighbours. This model, that in the following we will denote as RP (reinforcement process), is non-Markovian. Memory is explicitly introduced in the egonetwork dynamics as each node keeps remembering the list of already established ties. We fix c = 1 for all the nodes and we leave the generalization of the model where this value is correlated with node properties for future studies (indeed we show in the SM how the emerging network properties are changing for different values of c).
A side by side comparison of the time-aggregated representations of networks generated by the ML and RP models (using the same parameters) is shown in Fig. 4-a and b. The ML dynamics (Fig. 4.a) induces an aggregated network with a degree distribution P(k) ∝ k−γ where γ = ν and a weight distribution decaying exponentially23,55. This is also confirmed by large scale simulation results reported in Fig. 1.d and e (dashed lines). In case of the RP dynamics (Fig. 4.b), the memory process induces a considerably different structure. These effects are quantified in Fig. 1.d, e and f (solid lines). We observe a degree distribution that is heavy-tailed but more skewed in the RP model than the ML. This distribution is qualitatively matching the corresponding empirical measure in Fig. 1.a. Furthermore, the RP model generates heterogeneous weight distributions (see Fig. 1.e solid line) capturing extremely well real data. This is not the case in the ML model where the absence of memory induces exponential weight distributions far from reality (see Fig. 1.e dashed line). The RP dynamics not only induces realistic heterogeneities in the network structure, but also controls the evolution of the macroscopic network components. Indeed, due to the reinforcement mechanism, the largest connected component (LCC) in RP networks grows considerably slower than in the case of ML models (for illustration see Fig. 5.a). This is an important feature because dynamical process evolving on time-varying networks will progress with a time-scale that cannot be smaller than the LCC growth time-scale. As consequence, dynamical phenomena taking place on time-varying networks with memory will evolve at a slower rate than in memoryless time-varying networks. In the case of epidemic spreading for example, the memory in individuals' connections patterns shifts the epidemic threshold to larger values and more in general reduces the final number of infected nodes (see SM for details).
Rumour spreading processes in (a) ML and (b) RP activity-driven networks.
Node colors describe their states as ignorant (blue), spreader (red) and stifler (yellow). Node sizes, color and width of edges represent the corresponding degrees and weights. The parameters of the simulations are the same for the two processes: N = 300, T = 900, λ = 1.0 and α = 0.6. The processes were initiated from a single seed with maximum strength.
In panel (a) we show the sizes of the largest connected components (LCC) as a function of time for time aggregated ML and RP networks.
Simulations were run with the same parameters considering N = 105 nodes. In panel (b) we show the stifler r(t) density in rumor spreading simulations in ML (main panel, blue dashed line) and RP (main panel, purple solid line) networks with N = 105 nodes. We set λ = 1.0 and α = 0.6 and run the simulations for T = 105 time steps. The rumor spreading processes were simulated with the same parameters on aggregated ML (inset, yellow dashed line) and RP (inset, brown solid line) networks integrated for T time steps.
Rumour spreading processes on activity-driven networks
In order to study the effects of the emergence of strong ties on dynamical processes taking place in the network, we consider the classic rumor spreading process38. In this scheme, each node can be in three possible states; ignorant (I), spreader (S) or stifler (R). We denote the densities of individuals in each state at time t as i(t) = I(t)/N, s(t) = S(t)/N and r(t) = R(t)/N accordingly. At T = 0 everyone is ignorant except the selected single or multiple seeds who are set to be spreaders. At the time of an interaction the states of connected nodes can change by the following rules: (a)  or (b)
or (b)  or (c)
or (c)  . Here λ and α are the transition rates into the states of spreader or stifler accordingly. In all measurement (if it is not noted otherwise) we set λ = 1 and use α as a parameter. We assume that only their ratio matters for the spreading behaviour (supporting results are summarized in SM). Using these rules the spreaders communicate with probability λ the rumor to connected agents that become spreaders on their turn. If the spreaders however find that a contacted agent is already aware of the rumours, with probability α loose interest in the rumours and stop spreading it thus becoming a stifler. In the long run the system always reaches an equilibrium state where all spreaders have turned into stiflers, ∂ti(t) = 0 and ∂tr(t) = 0. Different parameters provide different penetration of the rumor in the network. Interesting quantities to study are the velocity of spreading of the rumor and the total number of agents aware of the gossip at the end of the process (stiflers).
. Here λ and α are the transition rates into the states of spreader or stifler accordingly. In all measurement (if it is not noted otherwise) we set λ = 1 and use α as a parameter. We assume that only their ratio matters for the spreading behaviour (supporting results are summarized in SM). Using these rules the spreaders communicate with probability λ the rumor to connected agents that become spreaders on their turn. If the spreaders however find that a contacted agent is already aware of the rumours, with probability α loose interest in the rumours and stop spreading it thus becoming a stifler. In the long run the system always reaches an equilibrium state where all spreaders have turned into stiflers, ∂ti(t) = 0 and ∂tr(t) = 0. Different parameters provide different penetration of the rumor in the network. Interesting quantities to study are the velocity of spreading of the rumor and the total number of agents aware of the gossip at the end of the process (stiflers).
Here we are interested in studying the differences on the final contagion densities in networks with or without memory (Fig. 5.b main panel), all other parameters of the rumor spreading model being equal. We set λ = 1.0 and α = 0.6 and in the case of ML networks at the end of the rumor spreading ~85% of the network is aware of the rumor. Instead, in the RP case the final contagion proportion is only slightly more than 60% of the total nodes. This hampering of the contagion process is also shown in Fig. 4.a and b for the same set of parameters. The differences are evident not only in the diffusion patterns, but also in the level of contagion. In the RP network, the rumor has spread only locally and reached 6 nodes other than the seed, while during the same time in the ML network the information reached 92 nodes out of 300.
To investigate in more details rumor spreading processes on different activity-driven models, we perform further simulations using different initial conditions and varying the rumours model parameters. In particular, we initiate the spreading from (i) the most active seed, (ii) one randomly selected seed or (iii) ten random seeds. We then simulate each process for T = 5 × 104 time steps and measure the average final proportion of nodes aware of the rumor 〈req〉. In each case, we perform 103 (or 104 for smaller systems) simulations in identically parametrized ML and RP networks, where the process lasts at least 103 steps. To highlight differences arising between the rumor propagation processes evolving on the two network dynamics, we kept λ = 1 and calculate the  ratios as function of α. Results in Fig. 6 indicate marginal size effects but strong dependence on the initial conditions. All corresponding ratios are decreasing with α, highlighting increasing differences between the fraction of population reached by the rumor in the two network dynamics. The largest differences are observed for a single initial seed, especially in the case of the most active nodes. These numerical findings can be understood by considering that the rumor spreading and the reinforcement process are occurring on comparable time scales. The reinforcement mechanism induces recurrent interactions that enhance the cessation of rumor spreading by “pair annihilation” of nodes connected by strong ties. This effect is controlled by α and can induce up to ~45% relative difference in the population reached by the rumor in the case of the RP model.
ratios as function of α. Results in Fig. 6 indicate marginal size effects but strong dependence on the initial conditions. All corresponding ratios are decreasing with α, highlighting increasing differences between the fraction of population reached by the rumor in the two network dynamics. The largest differences are observed for a single initial seed, especially in the case of the most active nodes. These numerical findings can be understood by considering that the rumor spreading and the reinforcement process are occurring on comparable time scales. The reinforcement mechanism induces recurrent interactions that enhance the cessation of rumor spreading by “pair annihilation” of nodes connected by strong ties. This effect is controlled by α and can induce up to ~45% relative difference in the population reached by the rumor in the case of the RP model.
In order to understand the biases induced in the dynamical properties of rumor spreading processes by the time aggregated representation of the networks, we consider topologies generated by a time-aggregated view of ML and RP models (see Fig. 5.b inset) and compare the results with their time-varying counterparts (see Fig. 5.b main panel). The results obtained show striking differences between the velocity of spreading. Indeed, the time for the rumor to reach a consistent fraction of nodes varies four orders of magnitudes in the two cases, with a very slow spreading dynamics in time-varying networks. Interestingly, this behaviour is general to all spreading processes. The observed results indicate a clear difference between the dynamical properties of processes taking place on time aggregated or time resolved networks. Our findings confirm that, when the time-scale of the processes is comparable with the evolution of the network, static representations of the system might introduce strong biases on the correct characterization of the phenomenon.
Rumour spreading processes on real time-varying networks
To verify the picture emerging from synthetic time-varying networks, we study the properties of rumor spreading processes in a real world time-varying system. In particular, we consider the MPC dataset and simulate the rumor spreading by using the actual sequence of calls (for more details see Methods)16. At the same time to directly contrast the role of memory and repeated interactions we defined a random null model defined by keeping the caller of each event as it appears in the MPC dataset, but selecting a callee randomly. In this way, we obtain a sequence recovering the original activities and shuffled egocentric networks. Furthermore, inter-event correlations are removed. The corresponding simulation results in Fig. 7.a shows a clear difference in the speed of spreading and final density of stifler nodes. While in the null model everyone becomes stifler at the end of the simulation, by using the original interaction sequences less than 40% of the network is aware of the rumor. This effect is even more clear in Fig. 7.b where their relative difference is rapidly increasing and becomes several orders of magnitude larger for larger α values. Different initial conditions are playing similar roles as we observed in synthetic networks. The effect of memory and repetitive interactions are the strongest if we initiate the rumor from the most active individual. We observed similar but weaker effects selecting a single or multiple random seeds.
In panel (a) we show the stifler r(t) density in data-driven rumor spreading simulations run on top of the MPC dataset (purple solid line) and the MPC null model (blue dashed line) with α = 0.1.
Panel (b) depicts the  ratios of average stifler densities at equilibrium. Simulations of panels (a) and (b) were run with various initial conditions (see legend) and averaged over 103 realizations. In panels (c) and (d) we plot the surviving probability, Ps(t), of rumor spreading processes initiated from a single random seed in the real MPC sequence and the MPC null model respectively. Probability values of panels (c) and (d) were averaged over 104 realizations.
ratios of average stifler densities at equilibrium. Simulations of panels (a) and (b) were run with various initial conditions (see legend) and averaged over 103 realizations. In panels (c) and (d) we plot the surviving probability, Ps(t), of rumor spreading processes initiated from a single random seed in the real MPC sequence and the MPC null model respectively. Probability values of panels (c) and (d) were averaged over 104 realizations.
We also measure the surviving probability Ps(t) defined as the probability that a rumor spreading process survives (still contains nodes actively spreading the rumor) up to time t56,57. We show Ps(t) for different α in Fig. 7.c. The initial scaling of Ps(t) shows that generally the rumor can spread only locally due to repeated interactions occurring on strong links between the seed and its neighbourhood. A very different behaviour emerges if we remove the effect of memory and repeated interactions considering the same quantities measured on the null model (see Fig. 7.d). Here, as the initial effect of repeated interactions vanishes and all realizations survive until the rumor covers the whole network. Note that similar results were obtained for activity-driven model processes presented in the SM. This highlights the significant role of recurrent interactions via strong ties. They play as bottleneck for the information propagation controlling the global outbreak of rumor spreading phenomena.
Discussion
We have presented the study of a large scale dataset of social interactions via mobile phone calls. We provided a simple empirical characterization of the effects of memory in its microscopic dynamical evolution. Considering the empirical evidences, we defined a novel generative model for time-varying networks with memory. The model mirrors many of the structural properties observed in the real network, like degree and weight heterogeneities and shows the spontaneous emergence of non-trivial connectivity patterns characterized by strong and weak ties. We characterize the effects of non-Markovian and heterogeneous connectivity patterns on rumor spreading processes. Interestingly, we find that strong ties are responsible for constraining the rumor diffusion within localized groups of individuals. This evidence points out that strong ties may have an active role in weakening the spreading of information by constraining the dynamical process in clumps of strongly connected social groups. The presented results underline the subtleties inherent to the analysis of dynamical processes in time-varying networks. No one-fits-all picture exists and a classification of dynamical process behaviour calls for a thorough analysis of each particular processes and networks considered. Furthermore, several extensions of the utilized framework of activity-driven networks are possible. Examples are node-node correlations, heterogeneous dynamics and bursty behaviour of nodes. The present study thus offers potential avenues for the study of dynamical processes in time-varying networks in complex settings where the memory of agents plays a determinant role in the evolution of the connectivity patterns of the system.
Methods
Dataset
The utilized dataset consists of 633, 986, 311 time stamped mobile-phone call (MPC) events recorded during 182 days with 1 second resolution between 6, 243, 322 individuals connected via 16, 783, 865 edges. The dataset was recorded by a single operator with 20% market share in an undisclosed European country (ethic statement was issued by the Northeastern University Institutional Review Board). To consider only true social interactions and avoid commercial communications we used interactions between users who had at least one pair of mutual interactions.
Data-driven model
In data-driven simulations we initiated the rumor spreading from a randomly selected call event of a randomly selected user in the MPC network. We then run the process for the length of the recorded period. When a realization arrived to the last event of the sequence, we used a periodic temporal boundary condition as we continued the process with the first event of the sequence16. However, as the simulations were executed no longer than the recorded time period, no event was used twice during one simulation run.
References
Lazer, D. et al. Computational social science. Science 323, 721 (2009).
Vespignani, A. Modeling dynamical processes in complex socio-technical systems. Nature Physics 8, 32–30 (2012).
Butts, C. Relational event framework for social action. Sociological Methodology 38, 155–200 (2008).
Newman, M. Networks: An Introduction (Oxford University Press, USA, 2010), 1 edn. URL http://www.worldcat.org/isbn/0199206651.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: Structure and dynamics. Physics Reports 424, 175 (2006).
Christakis, N. A. & Fowler, J. The spread of obesity in a large social network over 32 years. New England Journal of Medicine 357, 370–379 (2007).
Barrat, A., Barthélemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge University Press, 2008), 1 edn. URL http://www.worldcat.org/isbn/0521879507.
Aral, S., Muchnik, L. & Sundararajan, A. Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proceedings of the National Academy of Sciences 106, 21544–21549 (2009).
Volz, E. & Meyers, L. A. Epidemic thresholds in dynamic contact networks. J. R. Soc. Interface 6, 233–241 (2009).
Morris, M. Telling tails explain the discrepancy in sexual partner reports. Nature 365, 437 (1993).
Morris, M. Sexually Transmitted Diseases, Holmes, K. K., et al. Eds. (McGraw-Hill, 2007).
Clauset, A. & Eagle, N. Persistence and periodicity in a dynamic proximity network. In: DIMACS Workshop on Computational Methods for Dynamic Interaction Networks, 1–5 (2007).
Rocha, L. E. C., Liljeros, F. & Holme, P. Simulated epidemics in an empirical spatiotemporal network of 50,185 sexual contacts. PLoS Comput Biol 7, e1001109 (2011).
Isella, L. et al. What's in a crowd? analysis of face-to-face behavioral networks. J. Theor. Biol 271, 166 (2011).
Stehlé, J. et al. Simulation of an seir infectious disease model on the dynamic contact network of conference attendees. BMC Medicine 9 (2011). URL http://www.biomedcentral.com/1741-7015/9/87.
Karsai, M. et al. Small but slow world: How network topology and burstiness slow down spreading. Physical Review E 83, 025102 (2011). URL http://dx.doi.org/10.1103/PhysRevE.83.025102.
Miritello, G., Moro, E. & Lara, R. Dynamical strength of social ties in information spreading. Physical Review E 83, 045102 (2011). URL http://dx.doi.org/10.1103/PhysRevE.83.045102.
Fujiwara, N., Kurths, J. & Díaz-Guilera, A. Synchronization in networks of mobile oscillators. Physical Review E 83, 025101 (2011).
Parshani, R., Dickison, M., Cohen, R., Stanley, H. E. & Havlin, S. Dynamic networks and directed percolation. EPL (Europhysics Letters) 90, 38004 (2010). URL http://stacks.iop.org/0295-5075/90/i=3/a=38004.
Bajardi, P., Barrat, A., Natale, F., Savini, L. & Colizza, V. Dynamical patterns of cattle trade movements. PLoS ONE 6, e19869 (2011).
Baronchelli, A. & Díaz-Guilera, A. Consensus in networks of mobile communicating agents. Phys. Rev. E 85, 016113 (2012).
Starnini, M., Baronchelli, A., Barrat, A. & Pastor-Satorras, R. Random walks on temporal networks. Phys. Rev. E 85, 056115 (2012).
Perra, N., Gonçalves, B., Pastor-Satorras, R. & Vespignani, A. Activity driven modeling of time varying networks. Sci. Rep. 2, 469; 10.1038/srep00469 (2012).
Perra, N. et al. Random Walks and Search in Time-Varying Networks. Phys. Rev. Lett. 109, 238701 (2012). URL http://arxiv.org/abs/1206.2858. 1206.2858.
Ribeiro, B., Perra, N. & Baronchelli, A. Quantifying the effect of temporal resolution on time-varying networks. Sci. Rep. 3, 3006; 10.1038/srep03006 (2013).
Liu, S., Baronchelli, A. & Perra, N. Contagion dynamics in time-varying metapopulations networks. Physical Review E 87, 032805 (2013).
Hoffmann, T., Porter, M. & Lambiotte, R. Generalized master equations for non-poisson dynamics on networks. Physical Review E 86, 046102 (2012).
Pfitzner, R., Scholtes, I., Garas, A., Tessone, C. & Schweitzer, F. Betweenness preference: Quantifying correlations in the topological dynamics of temporal networks. Phys. Rev. Lett. 110, 19 (2013).
Morris, M. & Kretzschmar, M. Concurrent partnerships and transmission dynamics in networks. Social Networks 17, 299 (1995).
Toroczkai, Z. & Guclu, H. Proximity networks and epidemics. Physica A 378, 68 (2007).
Butts, C. Revisting the foundations of network analysis. Science 325, 414–416 (2009).
Rocha, L. E. C., Decuyper, A. & Blondel, V. D. Epidemics on a stochastic model of temporal network (2012). URL http://arxiv.org/abs/1204.5421. 1204.5421.
Handcock, M. S. Dynamic social network modeling and analysis. Breiger, K. M., Carley, P. Pattison Eds. National Academies, Washington, DC 229–240 (2003).
Holme, P. & Saramäki, J. Temporal networks. Physics Reports (2012).
Brandes, U., Lerner, J. & Snijders, T. Networks evolving step by step: Statistical analysis of dyadic event data. In: nternational Conference on Advances in Social Networks Analysis and Mining, 200–205 (2009).
Nooy, D. Signs over time: Statistical and visual analysis of a longitudinal signed network. Journal of Social Structure 9 (2008).
Onnela, J. P. et al. Structure and tie strengths in mobile communication networks. Proceedings of the National Academy of Sciences 104, 7332–7336 (2007).URL http://dx.doi.org/10.1073/pnas.0610245104 physics/0610104v1.
Daley, D. J. & Kendall, D. G. Epidemics and Rumours. Nature 204, 1118 (1964). URL http://dx.doi.org/10.1038/2041118a0.
Maki, D. P. & Thompson, M. Mathematical models and applications: with emphasis on the social, life and management sciences (Prentice-Hall, 1973).
Granovetter, M. The strength of weak ties. Am. J. Sociol. 78, 1360–1380 (1973).
Wasserman, S. & Faust, K. Social Network Analysis: Methods and Applications. Structural analysis in the social sciences, 8 (Cambridge University Press, 1994), 1 edn. URL http://www.worldcat.org/isbn/0521387078.
Barrett, L., Dunbar, R. & Lycett, J. Human Evolutionary Psychology (Princeton University Press, 2002). URL http://www.worldcat.org/isbn/0691096228.
Degenne, A. & Forse, M. Introducing Social Networks (Introducing Statistical Methods series) (Sage Publications Ltd, 1999), 1 edn. URL http://www.worldcat.org/isbn/0761956042.
Fisher, D. Using Egocentric Networks to Understand Communication. IEEE Internet Computing 9, 20–28 (2005). URL http://dx.doi.org/10.1109/MIC.2005.114.
Newman, M. E. J. Ego-centered networks and the ripple effect. Social Networks 25, 83–95 (2003). URL http://dx.doi.org/10.1016/S0378-8733(02)00039-4.
Karsai, M., Kaski, K. & Kertész, J. Correlated Dynamics in Egocentric Communication Networks. PLoS ONE 7, e40612 (2012). URL http://dx.doi.org/10.1371/journal.pone.0040612.
Gonçalves, B., Perra, N. & Vespignani, A. Modeling users' activity on twitter networks: Validation of Dunbar's number. PLoS ONE 6, e22656 (2011). URL http://dx.doi.org/10.1371/journal.pone.0022656.
Miritello, G. et al. Time as a limited resource: Communication strategy in mobile phone networks. arXiv:1301.2464 (2012).
Krings, G., Karsai, M., Bernhardsson, S., Blondel, V. D. & Saramäki, J. Effects of time window size and placement on the structure of an aggregated communication network. EPJ Data Science 1, 4 (2012). URL http://www.epjdatascience.com/content/1/1/4.
Hoppe, K. & Rodgers, G. J. Mutual selection in time-varying networks. Phys. Rev. E 88, 042804 (2013).
Cattuto, C. et al. Dynamics of Person-to-Person Interactions from Distributed RFID Sensor Networks. PLoS ONE 5, e11596 (2010). URL http://dx.doi.org/10.1371/journal.pone.0011596.
Chmiel, A., Kowalska, K. & Holyst, J. A. Scaling of human behavior during portal browsing. Physical Review E 80, 066122 (2009). URL http://dx.doi.org/10.1103/PhysRevE.80.066122.
Stehlé, J., Barrat, A. & Bianconi, G. Dynamical and bursty interactions in social networks. Physical Review E 81, 035101 (2010). URL http://dx.doi.org/10.1103/PhysRevE.81.035101.
Karsai, M., Kaski, K., Barabási, A.-L. & Kertész, J. Universal features of correlated bursty behaviour. Sci. Rep. 2, 397; 10.1038/srep00397 (2012).
Starnini, M. & Pastor-Satorras, R. Topological properties of a time-integrated activity-driven network. Phys. Rev. E 87, 062807 (2013).
Marro, J. & Dickman, R. Nonequilibrium Phase Transitions in Lattice Models (Collection Alea-Saclay: Monographs and Texts in Statistical Physics) (Cambridge University Press, 1999). URL http://www.worldcat.org/isbn/0521480620.
Satorras, R. P. & Vespignani, A. Epidemic Spreading in Scale-Free Networks. Physical Review Letters 86, 3200–3203 (2001). URL http://dx.doi.org/10.1103/PhysRevLett.86.3200.
Acknowledgements
This work has been partially funded by the NSF CCF-1101743 and NSF CMMI-1125095 awards. We acknowledge support from the FET project MULTIPLEX 317532 and MK acknowledges support from EUs 7th Framework Programs FET-Open ICTeCollective project (No. 238597). We thank A.-L. Barabási for the dataset used in this research. We thank B. Ribeiro, R. Burioni and A. Vezzani for useful discussions.
Author information
Authors and Affiliations
Contributions
M.K., N.P. and A.V. designed the research and participated in the writing of the manuscript. M.K. analysed the empirical data, performed the numerical calculations and completed the corresponding analytical derivations.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Materials
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Karsai, M., Perra, N. & Vespignani, A. Time varying networks and the weakness of strong ties. Sci Rep 4, 4001 (2014). https://doi.org/10.1038/srep04001
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04001
This article is cited by
-
Telling functional networks apart using ranked network features stability
Scientific Reports (2022)
-
A Fast Transform for Brain Connectivity Difference Evaluation
Neuroinformatics (2022)
-
Emergence and evolution of social networks through exploration of the Adjacent Possible space
Communications Physics (2021)
-
Temporal properties of higher-order interactions in social networks
Scientific Reports (2021)
-
Spreading of performance fluctuations on real-world project networks
Applied Network Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.









 ratios of average stifler densities at equilibrium.
ratios of average stifler densities at equilibrium.