Abstract
The motion of particles in random potentials occurs in several natural phenomena ranging from the mobility of organelles within a biological cell to the diffusion of stars within a galaxy. A Brownian particle moving in the random optical potential associated to a speckle pattern, i.e., a complex interference pattern generated by the scattering of coherent light by a random medium, provides an ideal model system to study such phenomena. Here, we derive a theory for the motion of a Brownian particle in a speckle field and, in particular, we identify its universal characteristic timescale. Based on this theoretical insight, we show how speckle light fields can be used to control the anomalous diffusion of a Brownian particle and to perform some basic optical manipulation tasks such as guiding and sorting. Our results might broaden the perspectives of optical manipulation for real-life applications.
Similar content being viewed by others
Introduction
Various phenomena rely on particles performing stochastic motion in random potentials. Examples range from the nanoscopic world of molecules undergoing anomalous diffusion within the cytoplasm of a cell1 to the Brownian motion of stars within galaxies2. Another example of this kind of phenomena is given by the motion of a Brownian particle in a random optical potential generated by a speckle pattern, i.e., the random light field resulting from complex light scattering in optically complex media, such as biological tissues, turbid liquids and rough surfaces (see background in Figure 1a–c)3,4. This latter example is particularly suited to work as a model system because its parameters (e.g., particle size and material, illumination light) are easily controllable and its dynamics are easily accessible by standard optical microscopy techniques5. Earlier experimental works showed the possibility of trapping particles in high-intensity speckle light fields6,7,8,9, the simplest optical manipulation task and the emergence of superdiffusion in an active media constituted by a dense solution of microparticles that generates a time-varying speckle field10. However, apart from these previous studies, there is little understanding of the interaction of Brownian motion with random light potentials and the intrinsic randomness of speckle patterns is largely considered a nuisance to be minimized for most purposes, e.g., in optical manipulation11,12. In fact, similar and even more complex effects have been extensively studied using periodic potentials rather than random potentials: these studies include the observation of giant diffusion induced by an oscillating periodic potential13 and the demonstration of guiding and sorting particles using either moving periodic potentials14,15,16 or static periodic potentials in microfluidic flows17,18,19. It is not a priori obvious that the same phenomena that have been observed with periodic potentials can also arise with random potentials, as the statistical properties of random potentials fundamentally differ from those of periodic potentials. For example, in non-equilibrium statistical physics, the dynamics of a Brownian particle in a moving periodic potential can be described as a straightforward generalization of the dynamics of a Brownian particle in static not out-of-equilibrium potentials, while this is no longer the case for random potentials for which a full out-of-equilibrium description is still required20.
Subdiffusion in a static speckle pattern.
(a–c) The background represents a speckle pattern generated by a circular aperture (λ = 1064 nm, speckle grain 490 nm); the white scale bar corresponds to 2 μm. The trajectories (green solid lines) show progressive confinement of a polystyrene bead (R = 250 nm, np = 1.59) in water (nm = 1.33, η = 0.001 Ns/m2, T = 300 K) as a function of the increasing speckle intensity corresponding to an average force on the particle of (a) 〈F〉 = 10 fN (〈I〉 = 13 mW/μm2), (b) 〈F〉 = 50 fN (〈I〉 = 65 mW/μm2), (c) 〈F〉 = 200 fN (〈I〉 = 260 mW/μm2). (d) Normalized autocorrelation function of the force field produced by the speckle pattern according to our theoretical model (solid line) and in the simulated speckle pattern (circles). The dashed line represents the theoretical normalized autocorrelation function of the speckle pattern intensity. (e) Brownian particle mean square displacements as a function of 〈F〉 (purple lines) and their deviation from Einstein's free diffusion law (black line).
In this Letter, we study the Brownian motion of a particle in a speckle pattern and, in particular, we derive the characteristic timescale τ of such motion, which is universal as it depends only on the universal properties of speckle light fields3,21,22. This theoretical insight permits us to demonstrate that random potentials can also be used instead of more regular potentials to control the dynamics of a Brownian particle in a very accurate way, despite their intrinsic randomness. First of all, while the emergence of superdiffusion in time-varying speckle patterns has already been observed10, we demonstrate that speckle fields provide a tunable and controllable model system to study anomalous diffusion by relating τ to the emergence of subdiffusion and superdiffusion in time-varying speckle patterns. Moreover, we demonstrate the possibility of harnessing the memory effect of speckle fields21,22 to perform basic optical manipulation tasks such as guiding and sorting23, which go beyond selective optical trapping in high-intensity speckle grains7,8.
Results
Speckle light patterns can be generated by different processes, such as scattering of a laser on a rough surface, multiple scattering in an optically complex medium, or mode-mixing in a multimode fiber4. In general, they are the result of the interference of a large number of waves propagating along different directions and with a random phase distribution, and, despite their random appearance, they share some universal statistical properties3,24 (see Supplementary Note S1). In particular, a speckle pattern has a negative exponential intensity distribution and the normalized spatial autocorrelation function CI(Δr) can be approximated by a Gaussian25:

where I(r) is the speckle pattern intensity as a function of the position r and the standard deviation σ ≈ d/3 is proportional to the average speckle grain size d (see Supplementary Note S1).
The motion of a Brownian particle in a static speckle field is the result of random thermal forces and deterministic optical forces. In the following discussion, we focus on particles whose radius is smaller than the light wavelength λ. We develop a theory that is strictly valid for Rayleigh particles (see Methods), but our conclusions hold also for larger particles26. In particular, as we show in the Supplementary Figure S1 using exact electromagnetic theory27,28, our theory is also approximately valid for bigger particles provided that their radius is smaller than the light wavelength λ. Optical gradient forces are the dominant deterministic forces acting on small particles and they attract high-refractive index particles towards the intensity maxima of the optical field26.
As a particle moves in a speckle field, the optical force acting on it changes both in magnitude and direction with a characteristic time scale  , where L is the correlation length of the optical force field and <v> is the average particle drift speed. The optical force field correlation function (Figure 1d) is
, where L is the correlation length of the optical force field and <v> is the average particle drift speed. The optical force field correlation function (Figure 1d) is

where  and α is the particle polarizability, so that
and α is the particle polarizability, so that  (see detailed derivation in Methods and Supplementary Note S2). Since the particle motion is overdamped29, the average particle drift speed is
(see detailed derivation in Methods and Supplementary Note S2). Since the particle motion is overdamped29, the average particle drift speed is  , where γ is the particle friction coefficient and
, where γ is the particle friction coefficient and  is the average force (see Supplementary Note S2). Thus, we obtain
is the average force (see Supplementary Note S2). Thus, we obtain

which is our central theoretical result and permits us to demonstrate how random optical fields can also be used instead of more regular ones to control the dynamics of a Brownian particle, despite the intrinsic randomness of the field. In the following, after considering how τ is related to the Brownian motion of a particle in a static speckle pattern, we will present two such examples via numerical experiments.
We start by considering the motion of a particle in a static speckle pattern. As shown by the trajectory in Figure 1a, when the optical forces are relatively low (average force 〈F〉 = 10 fN), the particle is virtually freely diffusing. As the forces increase (Figure 1b, 〈F〉 = 50 fN), first a subdiffusive behavior emerges where the particle is metastably trapped in the speckle grains, while it can still move between them30. Finally, for even stronger forces (Figure 1c, 〈F〉 = 200 fN), the particle remains trapped in one of the speckle grains for a very long time, as previously observed experimentally6,7,8,9. These observations can be interpreted in terms of τ: for relatively high forces (〈F〉 = 200 fN, τ ≈ 5.6 ms), τ is quite low which means that the particle, on average, experiences a restoring force towards its previous position quite soon in its motion, having little possibility to escape a speckle grain; for relatively low forces (〈F〉 = 10 fN, τ ≈ 112.5 ms) instead, τ is much higher which means that the particle has time to diffuse away from a speckle grain before actually experiencing the influence of the optical forces exerted by it. These qualitative considerations can be made more precise by calculating the mean square displacement MSD(Δt) of the particle motion (see Methods). As shown in Figure 1e, for low optical forces and high τ the mean square displacement is substantially linear in Δt, i.e. MSD(Δt) ≈ 4DSEΔt, where DSE is the Stokes-Einstein diffusion coefficient. As the forces increase and τ decreases, there is a transition towards a subdiffusive regime characterized by MSD(Δt) ∝ Δtβ with β < 1. We remark that, for very large Δt, the motion returns diffusive, i.e. β = 1, albeit with an effective diffusion coefficient Deff < DSE. Interestingly, in many naturally occurring anomalous diffusion processes, such as the subdiffusion of molecules within the living cell, the distribution of waiting times is expected to correspond to a random walker continually caught in potential wells whose depths are distributed exponentially1. Compared to periodic potentials, therefore, speckle patterns represent better model systems to study such phenomena: in fact, while periodic potentials are characterized by only a few potential depths, the distribution of potential depths (e.g. the distribution of intensities) in a speckle pattern follows a negative exponential distribution3,24.
We move now to an example of fundamental interest: the demonstration that using speckle patterns it is possible to control and tune anomalous diffusion continuously from subdiffusion to superdiffusion by employing a time-varying speckle pattern which changes over a timescale ξ similar to τ. A time-varying speckle pattern can result from a time-varying environment10, but can also be produced in a more controllable way by modulating spatially or spectrally the laser that generates it4. Here, we consider timescales for the speckle pattern variation in the order of microseconds or even slower: this is several orders of magnitude above the fluctuation timescales observed for incoherent light, which result in a loss of contrast and of the corresponding optical forces31. As can be seen in Figure 2a, different diffusive regimes emerge depending on the value of the ratio ξ/τ, thus allowing one to tune the diffusive behavior of the particle just relying on the external control of the speckle pattern time scale ξ. For ξ/τ ≫ 1, the speckle pattern motion is adiabatic so that the particle can reach its equilibrium distribution in the optical potential before the speckle field changes. This leads to a subdiffusive behavior, i.e., MSD(Δt) ∝ Δtβ with β < 1, as in a static speckle pattern. For ξ/τ ≪ 1, the particle cannot follow the fast variation of the speckle pattern so that the average optical force on the particle is zero leading to a diffusive behavior, i.e., MSD(Δt) ≈ 4DSEΔt. For ξ/τ ≈ 1, the particle is subject to time-varying forces, which can induce a superdiffusive behavior, i.e., MSD(Δt) ∝ Δtβ with β > 1. As in the case of the static speckle field, at long timescales, the particle motion will become again diffusive. Figure 2b highlights the transition from subdiffusion to superdiffusion by plotting  as a function of ξ/τ for various 〈F〉: if the resulting Deff > DSE, the particle has undergone superdiffusion. In this way, the diffusive behavior of a Brownian particle in a speckle field can be controlled by tuning the relevant adimensional parameter ξ/τ, thus providing a simple model system to study anomalous diffusion32, which has been shown to occur naturally, e.g., in the kinetics of single molecules in living cells1.
as a function of ξ/τ for various 〈F〉: if the resulting Deff > DSE, the particle has undergone superdiffusion. In this way, the diffusive behavior of a Brownian particle in a speckle field can be controlled by tuning the relevant adimensional parameter ξ/τ, thus providing a simple model system to study anomalous diffusion32, which has been shown to occur naturally, e.g., in the kinetics of single molecules in living cells1.
Superdiffusion in a time varying speckle pattern.
(a) Mean square displacements in logarithmic scale for a Brownian particle moving in a speckle pattern which varies on a timescale ξ ≈ τ (red line), ξ ≪ τ (orange line) and ξ ≫ τ (yellow line). The dots represent Einstein's free diffusion law. (b) The effective diffusion of the motion at long timescales as a function of ξ/τ shows a transition from subdiffusion (Deff < DSE) to superdiffusion (Deff > DSE). The maximum value of the superdiffusion appears for ξ ≈ τ (τ ≈ 22.5 ms for 〈F〉 = 50 fN, τ ≈ 11.2 ms for 〈F〉 = 100 fN and τ ≈ 5.6 ms for 〈F〉 = 200 fN). Every mean point is averaged over 500 particle trajectories 100 s long and whose initial position was randomly chosen within the speckle field. The gray shaded areas represent one standard deviation around the average values.
The second example is more applied and is the demonstration that it is possible to control the motion of a Brownian particle by using speckle fields, which sets the stage to perform optical manipulation tasks such as guiding particles in a particular direction, despite the randomness of the illumination. The relevant parameter for guiding is the ratio between the speckle pattern speed VS and the average drift velocity of the particle in a static speckle pattern  . As VS/〈v〉 increases, the average guiding velocity 〈vp〉 reaches a maximum for VS/〈v〉 ≈ 1, as shown in Figure 3a. A small speckle pattern translation up to a few micrometers can be implemented capitalizing on the speckle property known as memory effect21,22: for a speckle pattern generated by a thin sample, a small tilt of the illumination, easily achievable, e.g., with a galvanometric mirror or an acousto-optic deflector, entails a small spatial translation of the speckle pattern. As shown in Figure 3b, this is sufficient to realize a Brownian ratchet33: the speckle pattern repeatedly shifts first slowly (VS/〈v〉 = 1) by 1 μm in the positive direction, which exerts a strong drag on the particle and then fast (VS/〈v〉 = 10) back to the initial position, which has little effect on the particle position. In 250 ms, the particle is dragged by ≈3 μm in the direction of the speckle pattern shift, while the particle's trajectory in the perpendicular direction remains unaffected (Figure 3c).
. As VS/〈v〉 increases, the average guiding velocity 〈vp〉 reaches a maximum for VS/〈v〉 ≈ 1, as shown in Figure 3a. A small speckle pattern translation up to a few micrometers can be implemented capitalizing on the speckle property known as memory effect21,22: for a speckle pattern generated by a thin sample, a small tilt of the illumination, easily achievable, e.g., with a galvanometric mirror or an acousto-optic deflector, entails a small spatial translation of the speckle pattern. As shown in Figure 3b, this is sufficient to realize a Brownian ratchet33: the speckle pattern repeatedly shifts first slowly (VS/〈v〉 = 1) by 1 μm in the positive direction, which exerts a strong drag on the particle and then fast (VS/〈v〉 = 10) back to the initial position, which has little effect on the particle position. In 250 ms, the particle is dragged by ≈3 μm in the direction of the speckle pattern shift, while the particle's trajectory in the perpendicular direction remains unaffected (Figure 3c).
Guiding by the speckle memory effect.
(a) Average guiding velocity 〈vp〉 in the direction of the speckle pattern shift as a function of the shift speed VS for 〈F〉 = 200 fN (circles), 〈F〉 = 100 fN (triangles) and 〈F〉 = 50 fN (squares). The maximum 〈vp〉 is achieved for VS ≈ 〈v〉 (〈v〉 ≈ 10.5 μm/s for 〈F〉 = 50 fN, 〈v〉 ≈ 21.2 μm/s for 〈F〉 = 100 fN and 〈v〉 ≈ 42.4 μm/s for 〈F〉 = 200 fN). Every mean velocity point is calculated over 500 trajectories simulated during 10 s and whose initial position was randomly chosen within the speckle field. The gray shaded areas represent one standard deviation around the average values. (b) Speckle pattern shift and (c) particle displacement as a function of time in the direction of the speckle pattern shift x (black line) and in the orthogonal direction y (gray line). The speckle pattern repeatedly shifts first slowly in the positive direction by 1 μm and then fast to the initial position. The dashed lines represent the instant of time when there is a change of trend in the speckle pattern shift.
This guiding capability of a speckle pattern can be combined with standard microfluidic systems in order to perform tasks, such as sieving and sorting. For example, a static speckle pattern can be employed to realize a speckle sieve (Figure 4a and Supplementary Video S1). As a liquid containing 200 nm and 250 nm particles flows from left to right at 42 μm/s, a static speckle pattern efficiently holds the larger particles back while the smaller ones go through almost unaffected; interestingly, the size of the particle that are held back can be dynamically adjusted by changing the intensity of the speckle pattern. A spatiotemporal varying speckle field instead can be employed to realize a speckle sorter (Figure 4b and Supplementary Video S2). In a configuration similar to the one for the speckle sieve, the memory effect can be used to exert a perpendicular force to the flow selectively on the larger particles, so that each kind of particle gets guided into a different channel.
Microfluidic speckle sieve and speckle sorter.
(a) Lapse-time snapshots of the motion of polystyrene particles with radius R = 200 nm (〈F〉 = 90 fN, green dots) and R = 250 nm (〈F〉 = 46 fN, black dots) in a microfluidic speckle sieve, where a static speckle pattern (red shaded area) traps the smaller particles while it lets the larger particles go away with the flow (flow speed 42 μm/s, see also Supplementary Video S1). (b) Same as in (a), but with the speckle pattern ratcheting in the direction orthogonal to the flow by 1 μm (flow speed 34 μm/s, see also Supplementary Video S2). The black scale bar represents 50 μm.
Discussion
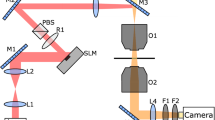
Using similar configurations, which are routinely used in microfluiduics, it is possible to separate particles on the basis of various parameters, such as their size or their refractive index, as shown in Supplementary Figures S2 and S3; the resolution of this optical fractionation17,18,19 is only limited by the size of the speckle field, i.e., the longer the speckle field the higher the sensitivity in particle's size or refractive index. These devices can, therefore, be scaled to achieve the high throughput or sensitivity needed in microfluidics (thousands of particles per second) by increasing the flow speed and laser power, as it is also the case for alternative optofluidics devices17,18,19. Moreover, an additional advantage of speckle patterns is that they are also intrinsically widefield and could be used to sort many particles in parallel in a broader microfluidic chamber, where flow speed is strongly reduced. From the experimental point of view, speckle light fields with such universal statistical properties are straightforwardly generated over large areas using different processes, such as scattering of a laser on a rough surface, multiple scattering in an optically complex medium, or mode-mixing in a multimode fiber4. In the Supplementary Note S3, we propose some possible setups that can be implemented at low cost, with little alignment and few optical components based on these processes of generation of a speckle field. Here, we have mainly considered possible experimental implementations where the Brownian particles are moving in a quasi 2-dimensional speckle pattern. This is particularly true for experiments that are designed satisfying one of the following conditions: the speckle field is generated with a low numerical aperture so that the average longitudinal extension of the speckle grain extends over the depth of the microfluidic channel; optical scattering forces push the particles in the direction of propagation of light, so that in the presence of a boundary, such as the glass or PDMS surface of a microchannel, they effectively confine the particles in a quasi two dimensional space34; or the motion of the particles is confined to a quasi 2-dimensional volume far from any physical boundary, for example, by employing acoustic standing waves35. In more complex settings, our results can be readily extended to take into account a 3-dimensional description of the speckle field24. Particular care should be paid to extent the speckle memory effect to a 3-dimensional case: while the standard memory effect achieves a lateral translation of the speckle field by adding a linear phase gradient at the input of a complex medium21,22, a longitudinal translation of the speckle field can be obtained by adding a quadratic phase gradient at the input36. Therefore a combination of these two effects allows one to translate the results of our work to a 3-dimensional situation.
In conclusion, we have developed a theoretical framework that allows one to convert the randomness of a speckle light field into a tunable tool to influence the motion of a Brownian particle. In particular, we performed numerical experiments to show the applicability of this concept to the tunable control of anomalous diffusion and to perform standard optical manipulation tasks, such as sorting and guiding. While some of the tasks we propose in the manuscript can be achieved using optical traps or lattices in periodic arrangements13,14,15,16,17,18,19, the alternative use of random potentials offers some additional advantages, such as intrinsic robustness to noise and aberrations from the optics and the environment. In fact, the use of random optical potentials over periodic ones has the advantage of requiring very simple optical setups as well as a very low degree of control over the experimental environment, thus offering the possibility of performing optical manipulation through scattering media, such as diffusers and biological tissue, where light propagation naturally leads to the formation of speckle patterns, without recurring to wavefront shaping11.
Methods
Simulation of Brownian motion in a speckle pattern
The motion of a Brownian particle of radius R in a generic force field can be modeled with the following Langevin equation37:

where  , m and γ = 6πηR are respectively the particle's velocity, mass and friction coefficient, η the viscosity of the surrounding medium, W a white noise vector, kB the Boltzmann constant and T the temperature of the system. For a Rayleigh particle, F(r) = κ∇I(r) where
, m and γ = 6πηR are respectively the particle's velocity, mass and friction coefficient, η the viscosity of the surrounding medium, W a white noise vector, kB the Boltzmann constant and T the temperature of the system. For a Rayleigh particle, F(r) = κ∇I(r) where  and α is the particle polarizability, which depends on the particle's volume, shape and composition38. For a spherical particle with radius R and refractive index np immersed in a liquid with refractive index nm,
and α is the particle polarizability, which depends on the particle's volume, shape and composition38. For a spherical particle with radius R and refractive index np immersed in a liquid with refractive index nm,  . Inserting the full expression of the force and neglecting inertial effects in the motion of the particle29, Equation (4) simplifies as:
. Inserting the full expression of the force and neglecting inertial effects in the motion of the particle29, Equation (4) simplifies as:

where  is the Stokes-Einstein's diffusion coefficient of the Brownian particle. Simulations of Brownian motion in the field of forces generated by a speckle pattern were therefore obtained by numerically solving Equation (5)39. In all simulations, the particles are polystyrene beads (np = 1.59) in water (nm = 1.33, η = 0.001 Ns/m2, T = 300 K). Due to the low scattering cross-section of the particles and their low concentration, we consider that the force field of the speckle pattern is not influenced by the particle. Even though we used a 2-dimensional model to simulate Brownian dynamics, our results can be readily extended to a 3-dimensional situation by considering a fully 3-dimensional description of the speckle pattern24,39. In the presence of a hard boundary, an effective diffusion constant and an effective friction coefficient must be included in the model40, while for the case of low density suspensions of Brownian particles multiple reflections are very small and can be safely neglected. In the presence of flow, we assumed laminar flow because of the low Reynolds numbers associated to microfluidc channels29,40. Every particle trajectory used in the data presented from Figure 1 to 3 was calculated over a different realization of speckle field. Moreover, the initial position for the trajectory was randomly chosen within the speckle field. In Figure 4, instead, we used the same speckle field and initial position for every simulated particle.
is the Stokes-Einstein's diffusion coefficient of the Brownian particle. Simulations of Brownian motion in the field of forces generated by a speckle pattern were therefore obtained by numerically solving Equation (5)39. In all simulations, the particles are polystyrene beads (np = 1.59) in water (nm = 1.33, η = 0.001 Ns/m2, T = 300 K). Due to the low scattering cross-section of the particles and their low concentration, we consider that the force field of the speckle pattern is not influenced by the particle. Even though we used a 2-dimensional model to simulate Brownian dynamics, our results can be readily extended to a 3-dimensional situation by considering a fully 3-dimensional description of the speckle pattern24,39. In the presence of a hard boundary, an effective diffusion constant and an effective friction coefficient must be included in the model40, while for the case of low density suspensions of Brownian particles multiple reflections are very small and can be safely neglected. In the presence of flow, we assumed laminar flow because of the low Reynolds numbers associated to microfluidc channels29,40. Every particle trajectory used in the data presented from Figure 1 to 3 was calculated over a different realization of speckle field. Moreover, the initial position for the trajectory was randomly chosen within the speckle field. In Figure 4, instead, we used the same speckle field and initial position for every simulated particle.
Mean square displacement calculation
The calculation of the MSD is performed according to  , where P(r,Δt) is the probability density function of finding a particle at position r at time Δt1. In practice, each MSD curve was obtained by averaging over 500 different particle trajectories that were simulated over 100 s after waiting enough time for the particles to thermalize in the random optical potential given by the speckle pattern.
, where P(r,Δt) is the probability density function of finding a particle at position r at time Δt1. In practice, each MSD curve was obtained by averaging over 500 different particle trajectories that were simulated over 100 s after waiting enough time for the particles to thermalize in the random optical potential given by the speckle pattern.
References
Barkai, E., Garini, Y. & Metzler, R. Strange kinetics of single molecules in living cells. Phys. Today 65, 29–35 (2012).
Chandrasekhar, S. Brownian motion, dynamical friction and stellar dynamics. Rev. Mod. Phys. 21, 383–388 (1949).
Goodman, J. W. Some fundamental properties of speckle. J. Opt. Soc. Am. 66, 1145 1150 (1976).
Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nature Photon. 6, 283–292 (2012).
Babic, D., Schmitt, C. & Bechinger, C. Colloids as model systems for problems in statistical physics. Chaos 15, 026114 (2005).
Boiron, D. et al. Trapping and cooling cesium atoms in a speckle field. Eur. Phys. J. D 7, 373–377 (1999).
Shvedov, V. G. et al. Laser speckle field as a multiple particle trap. J. Opt. 12, 124003 (2010).
Shvedov, V. G. et al. Selective trapping of multiple particles by volume speckle field. Opt. Express 18, 3137–3142 (2010).
Staforelli, J. P., Brito, J. M., Vera, E., Solano, P. & Lencina, A. A clustered speckle approach to optical trapping. Opt. Commun. 283, 4722–4726 (2010).
Douglass, K. M., Sukhov, S. & Dogariu, A. Superdiffusion in optically controlled active media. Nature Photon. 6, 834–837 (2012).
Čižmár, T., Mazilu, M. & Dholakia, K. In situ wavefront correction and its application to micromanipulation. Nature Photon. 4, 388–394 (2010).
Dholakia, K. & Čižmár, T. Shaping the future of optical manipulation. Nature Photon. 5, 335–342 (2011).
Lee, S. H. & Grier, D. G. Giant colloidal diffusivity on corrugated optical vortices. Phys. Rev. Lett. 96, 190601 (2006).
Ricárdez-Vargas, I., Rodríguez-Montero, P., Ramos-García, R. & Volke-Sepúlveda, K. Modulated optical sieve for sorting of polydisperse microparticles. Appl. Phys. Lett. 88, 121116 (2006).
Demergis, V. & Florin, E. L. High precision and continuous optical transport using a standing wave optical line trap. Opt. Express 19, 20833–20848 (2011).
Šiler, M., Čižmár, T. & Zemánek, P. Speed enhancement of multi-particle chain in a traveling standing wave. Appl. Phys. Lett. 100, 051103 (2012).
McDonald, M. P., Spalding, G. C. & Dholakia, K. Fractionation of polydispersed colloid with acousto-optically generated potential energy landscapes. Nature 426, 421–424 (2003).
Milne, G., Rhodes, D., McDonald, M. & Dholakia, K. Microfluidic sorting in an optical lattice. Opt. Lett. 32, 1144–1146 (2007).
Xiao, K. & Grier, D. G. Multidimensional optical fractionation of colloidal particles with holographic verification. Phys. Rev. Lett. 104, 028302 (2010).
De Groot, S. R. & Mazur, P. Non-equilibrium thermodynamics (Dover, New York, 1984).
Feng, S., Kane, C., Lee, P. A. & Stone, A. D. Correlation and fluctuations of coherent wave transmission through disordered media. Phys. Rev. Lett. 61, 834–837 (1988).
Freund, I., Rosenbluh, M. & Feng, S. Memory effects in propagation of optical waves though disordered media. Phys. Rev. Lett. 61, 2328–2331 (1988).
Jonáš, A. & Zemánek, P. Light at work: the use of optical forces for particle manipulation, sorting and analysis. Electrophoresis 29, 4813–4851 (2008).
Goodman, J. W. Speckle Phenomena in Optics: Theory and Applications. (Roberts and Co. Publishers, Greenwood Village, 2007).
Zhang, B., Zerubia, J. & Olivo-Marin, J. C. Gaussian approximations of fluorescence microscope point-spread function models. Appl. Opt. 46, 1819–1829 (2007).
Ashkin, A. History of optical trapping and manipulation of small-neutral particle, atoms and molecules. IEEE J. Sel. Top. Quant. El. 6, 841–846 (2000).
Nieminen, T. A. et al. Optical tweezers computational toolbox. J. Opt. A 9, S196–S203 (2007).
Borghese, F., Denti, P. & Saija, R. Scattering from model nonspherical particles (Springer, Heidelberg, 2007).
Purcell, E. M. Life at low Reynolds numbers. Am. J. Phys. 45, 3–11 (1977).
McCann, L. I., Dykman, M. & Golding, B. Thermally activated transitions in a bistable three-dimensional optical trap. Nature 402, 785–787 (1999).
Curry, N. et al. Direct determination of diffusion properties of random media from speckle contrast. Opt. Express 36, 3332–3334 (2011).
Bouchad, J. P. & Georges, A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Rep. Phys. 195, 127–293 (1990).
Rousselet, J., Salome, L., Ajdari, A. & Prost, J. Directional motion of Brownian particles induced by a periodic asymmetric potential. Nature 370, 446–448 (1994).
Mikhael, J., Roth, J., Helden, L. & Bechinger, C. Archimedean-like tilting on decagonal quasicrystalline surfaces. Nature 454, 501–504 (2008).
Thalhammer, G. et al. Combined acoustic and optical trapping. Biomed. Opt. Express 2, 2859–2870 (2011).
Ghielmetti, G. & Aegerter, C. M. Scattered light fluorescence microscopy in three dimensions. Opt. Express 20, 3744–3752 (2012).
Volpe, G., Volpe, G. & Petrov, D. Brownian motion in a nonhomogeneous force field and photonic force microscope. Phys. Rev. E 76, 061118 (2007).
Harada, Y. & Asukura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 124, 529–541 (1996).
Volpe, G. & Volpe, G. Simulation of a Brownian particle in an optical trap. Am. J. Phys. 81, 224–230 (2013).
Happel, J. & Brenner, H. Low Reynolds number hydrodynamics (Springer, New York, 1983).
Acknowledgements
The authors thank Andrew Griffiths and Patrick Tabeling for insightful discussions. Giovanni Volpe was partially supported by Marie Curie Career Integration Grant (MC-CIG) PCIG11 GA-2012-321726. Sylvain Gigan acknowledges funding from Agence Nationale de La Recherche (ANR-JCJC-ROCOCO), the City of Paris (Programme Emergence) and the European Research Council (under grant N°278025).
Author information
Authors and Affiliations
Contributions
G.V., G.V. and S.G. contributed to the original idea. G.V. and G.V. developed the theoretical model. G.V. (Giorgio Volpe) performed the numerical simulations. All authors discussed the results and contributed to the redaction of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Supplementary Information
Supplementary Video S1
Supplementary Information
Supplementary Video S2
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Volpe, G., Volpe, G. & Gigan, S. Brownian Motion in a Speckle Light Field: Tunable Anomalous Diffusion and Selective Optical Manipulation. Sci Rep 4, 3936 (2014). https://doi.org/10.1038/srep03936
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03936
This article is cited by
-
Fickian yet non-Gaussian diffusion of a quasi-2D colloidal system in an optical speckle field: experiment and simulations
Scientific Reports (2023)
-
Spatial coherence of light inside three-dimensional media
Nature Communications (2021)
-
High-performance reconstruction of microscopic force fields from Brownian trajectories
Nature Communications (2018)
-
Numerical study on trapping and guiding of nanoparticles in a flow using scattering field of laser light
Optical Review (2018)
-
Disorder-mediated crowd control in an active matter system
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.