Abstract
Electromagnetic resonances in conducting structures give rise to the enhancement of local fields and extinction efficiencies. Conducting structures are conventionally fabricated with a fixed geometry that determines their resonant response. Here, we challenge this conventional approach by demonstrating the photo-generation of THz linear antennas on a flat semiconductor layer by the structured optical illumination through a spatial light modulator. Free charge carriers are photo-excited only on selected areas, which enables the realization of different conducting antennas on the same sample by simply changing the illumination pattern, thus without the need of physically structuring the sample. These results open a wide range of possibilities for the all-optical spatial control of resonances on surfaces and the concomitant control of THz extinction and local fields.
Similar content being viewed by others
Introduction
The possibility of confining electromagnetic fields in subwavelength volumes has been a main motivation driving the current interest on optical plasmonics1,2,3. Optical antennas with localized resonances resulting from the coherent oscillation of conduction electrons are characterized by large local field enhancements in subwavelength volumes. One of the greatest challenges for optical antennas and plasmonics in general is the efficient and fast active control of resonant frequencies and local fields. Coherent control of local fields by temporally shaping optical pulses4,5 or by phase shaping of beams6,7,8 has been demonstrated. Ultrafast active control of surface waves has been also achieved by the transient modulation of the dielectric function. This modulation is attained by a pump laser that induces changes in the electron distribution function and the optical properties of the metal9,10,11,12,13,14, or by modifying the permittivity of the surrounding dielectric15. An alternative to metals for the active control of localized resonances at THz frequencies are high mobility doped semiconductors with metallic behavior in this frequency range16. Doped semiconductors have charge carrier densities orders of magnitude lower than in metals17,18,19, which enables the excitation of resonances at THz frequencies with a similar behavior to those of metals at near- and mid-infrared frequencies20,21,22,23. Moreover, this characteristic offers the possibility of actively tuning THz resonances from a plasmonic behavior to that of surface currents in perfect electrical conductors by controlling the carrier density16. This concept has been used to modify the propagation of surface waves24 and the resonant response of THz antennas27 and of metamaterials structured on top of semiconducting substrates25,26 by the photo-excitation of electrons across the semiconductor bandgap. Common to all these works is that electromagnetic fields are controlled in surfaces that have been physically structured with nano and micro-structures.
In this manuscript we demonstrate experimentally a full all-optical generation of linear antennas at THz frequencies. The photo-generation is realized by illuminating a thin GaAs layer with a laser beam shaped by a Spatial Light Modulator (SLM) to contain several micro antennas. This approach does not require any physical structuring of the sample and offers the unique possibility of controlling spatially and spectrally resonances and local fields by modifying the illumination pattern. Okada and coworkers have recently demonstrated the photo-generation of THz diffraction gratings on Si by illumination through a SLM28,29. Chatzakis et al. extended this work to GaAs gratings generated by illumination through an optical mask30. Also, THz beam steering using photoactive semiconductors has been recently demonstrated by Busch et al.31 and photo-generated metamaterials have been theoretically proposed by Rizza et al.32. These works have laid a solid background for the realization of all-optical active THz devices; However, they have not demonstrated experimentally the possibility of inducing resonant phenomena by the structured illumination of flat surfaces. Therefore, this manuscript constitutes a bridge between the emerging fields of active photonics and THz metamaterials.
Results
Setup and sample description
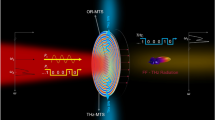
The measurements have been performed using time-resolved THz time-domain spectroscopy (see Methods). With this technique an optical pulse is used to pump a semiconductor while a time-delayed THz pulse probes the photoinduced changes in the conductivity of the semiconductor. A key element in our setup is a computer controlled SLM, which is used to structure the pump by spatially shaping the beam. The operation principle of the structured illumination is illustrated in Fig. 1(a). A horizontally polarized optical pulse (λ = 800 nm), indicated by the red beam in the figure, is transmitted through a polarizing beam splitter (PBS) and reflected back by the SLM. The SLM is a pixelated liquid crystal device (1920 × 1200 pixels), which rotates the polarization of the incident light. Light reflected from the so-called bright pixels undergoes a rotation of the polarization by 90°, being reflected by the PBS towards the sample; while light reflected from dark pixels maintains its polarization and it is transmitted back through the PBS, thus not reaching the sample. The intensity of the light reflected by each pixel of the SLM and by the PBS can be changed continuously from a maximum value (bright pixel) to a minimum (dark pixel). A lens (not shown in Fig. 1(a)) with a focal length of 150 mm is used to project (1:1) the structured beam onto the surface of the sample, which is a thin GaAs layer, where electrons are photo-excited from the valence to the conduction band only on the illuminated regions. A THz pulse, indicated by the yellow beam in Fig. 1(a), propagates collinearly with the optical pulse and transmitted through the sample. The pixel size on the surface of the sample is 8 × 8 μm2, being much smaller than the wavelength of THz radiation. Therefore, this technique is ideally suited for the optical generation of subwavelength THz structures.
(a) Schematic representation of the setup used for photo-generation of THz linear antennas. The optical pump is indicated by the red beam, whose profile is structured by the spatial light modulator (SLM). Collinear to the optical pump is a THz pulse represented by the yellow beam. (b) Photograph of the GaAs layer used as sample to photo-generate plasmonic antennas.
The sample used for the experiments consists of a layer of single crystalline undoped GaAs with a thickness of 1 μm bonded to a SiO2 substrate (see Methods). A photograph of the sample is shown in Fig. 1(b). Intrinsic GaAs has a dielectric behavior at THz frequencies. However, its real component of the permittivity becomes negative, hence GaAs becomes conducting, at 1 THz for carrier densities above 1.5 × 1016 cm−3. These carrier densities are easy to reach by pumping the sample with an optical pulse of moderate fluence. The high electron mobility of intrinsic GaAs at room temperature (~ 7000 cm2V−1s−1), favors the excitation of localized SPPs. Moreover, the small thickness of the semiconductor slab, which is comparable to the optical absorption length of GaAs (La = 0.7 μm at λ = 800 nm), allows the (nearly) homogeneous excitation of carriers as a function of the depth in the layer. For the experiments we used pump fluences up to 80 μJ/cm2, which excites ~ 1018 cm−3 free carriers on the bright pixels of the illuminated pattern. The carrier density in GaAs at the regions illuminated by dark pixels is lower than 1016 cm−3. Therefore, optical pumping of GaAs with a shaped beam results into the local change of the permittivity from an insulating to a conducting state.
Photo-generated THz antennas
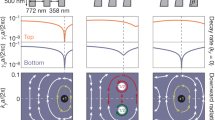
To demonstrate the photo-generation of THz antennas on the GaAs layer we have measured the THz extinction spectra of random arrays of rods with the same orientation generated at a fixed optical fluence while varying their lengths. We have also measured arrays of rods with the same length but generated with different fluences. Figure 2(a) shows an image of an array of rods. This image is taken by placing a CCD camera at the sample position. Their random distribution suppresses any effect due to periodicity in the THz extinction, while their horizontal alignment enables the excitation of antenna resonances for THz radiation incident with an horizontal polarization. A close view of a single linear antenna rod is shown in Fig. 2(b). The effective dimensions of the photo-excided antennas were defined by the FWHM of the pumped fluence. The illuminated area (filling fraction of the rods) corresponds to 18% of the surface. The spacing between two consecutive rods was chosen to be larger than 100 μm along the long axis of the rod and 40 μm along the short axis. These distances are large enough to minimize the near field coupling between consecutive rods33, while maximizing their filling fraction to increase the THz extinction.
(a) Image of a random array of photo-generated rods. (b) Close view image of a single rod. The upper and right plots are the intensity profiles along the horizontal and vertical dotted lines. The vertical axis and the color scale indicate the pump fluence in μJ/cm2. The dimensions of the rods are defined by the FWHM of the pump beam intensity marked by the vertical dashed lines.
For the THz extinction measurements the sample was first illuminated with a pump pulse with a center wavelength λ = 800 nm and a duration of 100 fs. Subsequently, a THz pulse was transmitted through the sample. The time delay between the optical pump and the arrival of the THz pulse was Δτp−p = 10 ps, which is sufficiently long to enable the relaxation of hot electrons to the lowest energy state of the conduction band34. Furthermore, this time delay was much shorter than the carrier recombination time, which was experimentally determined to be τr ~ 450 ps. The THz transmission amplitude is measured within a time window of 12 ps. Over this time window the carrier diffusion length is much shorter than all the characteristic lengths in the experiment, i.e., the dimensions of the structures and the THz wavelength. Therefore, the photo-excited antennas can be described in a first approximation as having stationary dimensions and carrier density.
We measure the zeroth order differential transmission transients, ΔE(t), i.e., the THz amplitude transient transmitted through the optically pumped sample in the forward direction minus the transmitted transient of the unpumped sample ΔE(t) = EP(t) − ENP(t). These measurements are done by chopping the pump beam at half the repetition rate of the laser, i.e., 500 Hz44. To gain spectral information about this transmission, the transients are Fourier transformed and squared to obtain the transmittance. The extinction  , defined as the sum of scattering and absorption, is given according to the optical theorem as one minus the zeroth-order transmittance. The latter is equal to the ratio of the pumped to the unpumped transmittance
, defined as the sum of scattering and absorption, is given according to the optical theorem as one minus the zeroth-order transmittance. The latter is equal to the ratio of the pumped to the unpumped transmittance  . Therefore,
. Therefore,  .
.
Figure 3 is the main result of this manuscript. Figure 3 (a) shows the extinction spectra of photo-generated THz antennas with a fixed dimension of 230 × 40 μm2 and varying optical pumping fluences. The polarization of the THz beam was set parallel to the long axis of the rods. A resonance appears in the extinction spectrum for optical fluences higher than 12 μJ/cm2. At this fluence the number of photo-excited carriers in GaAs is large enough to give a metallic behavior to the semiconductor in the THz frequency range. The maximum extinction reaches values higher than 65% while the illuminated fraction of the GaAs is only 18%. This enhanced extinction can be explained in terms of the large THz scattering cross section of the rods resulting from their antenna like behavior. The resonance can be associated to the fundamental antenna mode, which occurs when the length of the rod is approximately equal to half the effective wavelength of the mode, i.e., L = λ/(2neff) − 2δ, where λ is the vacuum wavelength, neff the effective refractive index of the THz antenna mode defining its phase velocity35 and δ is a parameter that leads to an apparent increase of the antenna length to L + 2δ due to the reactance at the ends35,36. This parameter depends in principle on the antenna width and on the materials defining the antenna and its surroundings. It is thus expected to change with the pump fluence as a consequence of the graded intensity along the edges of the rods. There is also a clear blue-shift of the resonance as the pump fluence increases. This blue-shift is a consequence of the increase in conductivity of the pumped GaAs and the evolution of the resonance from a plasmonic behavior to a behavior that approaches that of a perfect conductor16. Indeed, a larger conductivity results in a weaker penetration of the THz field in the pumped GaAs and a reduction of neff35. In the limit of perfect electric conductor the field does not penetrate into the metal and neff is defined by the dielectrics surrounding antenna.
The extinction spectra of photo-generated THz linear antennas with various lengths and a fixed width of 40 μm pumped at 70 μJ/cm2 is shown in Fig. 3 (b). A large red-shift of the resonance and increase of the extinction is observed as the length of the photo-generated rods is increased. In Fig. 4 we plot the rod length as a function of the resonant wavelength of maximum extinction. From the slope of the linear fit, illustrated by the solid line, we obtain neff = 1.84 ± 0.07, while the intersection of this fit with the ordinate axis equals −2δ with δ = 20.8 ± 3.9 μm.
A closer look to Fig. 3(b) reveals a shoulder at shorter wavelengths (around 300 μm) in the extinction spectrum of the longer rods. We attribute this shoulder, which is absent in the spectra of the shorter rods, to the excitation of the next higher order antenna mode in a rod by normal incident THz radiation, i.e., the 3λ/2neff mode37. The observation of multipolar photo-generated modes is a consequence of the high quality of the GaAs layer used for the experiments.
Discussion
To further investigate the localized modes associated to the photo-generated rods, we have performed Finite Difference in Time Domain (FDTD) simulations using a commercial software package (Lumerical Solutions). Details on the simulations can be found in the Methods. Figure 5 (a) shows the extinction spectra of the 230 μm and 80 μm long rods. To approximate the simulated geometry as much as possible to the experiment, we have considered a graded variation of the carrier concentration in the GaAs film at the boundaries of the rod from N = 2 × 1018 cm−3 at the core to N = 5 × 1015 cm−3 in the unpumped surrounding region, which resembles the illumination profiles shown in Fig. 2(b). As can be appreciated in Fig. 5(a), this geometry reproduces reasonably well the resonance wavelength and magnitude of the extinction. Figures 5 (b) and (c) show the near field enhancement at the GaAs-air interface and at the wavelengths of the maximum extinction for the 230 μm and 80 μm long rods respectively. The enhancement, defined as the near field intensity normalized to the incident intensity at the GaAs-air interface, has the dipolar character expected for the λ/(2neff) mode in the rod-shaped antennas. The maximum field enhancement, which is larger for the shorter rods, is achieved at the edges of the rods where the charge density is maximum.
Finite difference in time domain simulations of photo-generated rods.
(a) Simulated extinction for rods with effective dimensions 230 × 40 μm2 and 80 × 40 μm2. (b) simulated total field enhancement at the GaAs-air interface for a rod with an effective length of 230 μm. (c) same as (b) but for a rod with an effective length of 80 μm.
It is worthwhile to stress that the near-field enhancement in photo-generated antennas can be fully controlled in magnitude and spatial position by simply changing the illumination pattern defined with the SLM. By controlling the time delay between the optical pump and THz probe pulse, it is also possible to tune the magnitude of the enhancement. This approach could be exploited to enhance the sensitivity of locally functionalized surfaces or to realize spectroscopy of subwavelength structures by resonant enhancement of the local fields. Moreover, larger field enhancements could be achieved by coupling rods to form dimers22 or by defining bowtie antennas with sharp tips and small gaps27.
In conclusion, we have demonstrated the photo-generation of THz antennas by the structured illumination of a thin layer of undoped GaAs. This illumination is accomplished with a spatial light modulator that allows a full optical control of resonant frequencies and local field enhancements. This approach can be extended to the photo-generation of metamaterials exhibiting magnetic resonances, i.e., split ring resonators38, metasurfaces for active beam steering39 and THz wave guiding structures40.
Methods
GaAs layer fabrication
The sample was prepared utilizing epitaxial growth in an Aixtron 200 low pressure metal organic chemical vapour deposition reactor and subsequent layer transfer. The epitaxial structure composed of a 10 nm thick sacrificial AlAs layer followed by a 1 μm thick undoped GaAs layer was grown at a temperature of 650°C and a pressure of 20 mbar on a 2-inch diameter (001) GaAs wafer, 2 degrees off towards <110>. Source materials were trimethyl-gallium and trimethyl-aluminium as group-III precursors and arsine as group V precursor. After growth a flexible plastic support carrier was mounted on top of the GaAs epi-layer and the sample was subjected to a 20% HF solution in water for selective etching of the AlAs layer41. During the process the plastic carrier is used as a handle to bent away the GaAs epi-layer from the wafer ensuring optimal access of the HF solution to the 10 nm high etch front of the AlAs release layer42. After separation the GaAs thin-film is bonded to a 1 mm thick SiO2 substrate using a mercapto-ester based polymer. The thickness of this bonding layer is approximately 40 μm. Finally the plastic support carrier is removed leaving the 1 μm single crystal GaAs layer on a SiO2 substrate.
Permittivity values
The values of the permittivity of the SiO2 substrate and the bonding layer were experimentally determined in the frequency range of the measurements by measuring the time-domain THz transmission. This phase sensitive technique allows to obtain the complex permittivity from a single measurement provided that the thickness of the layers are precisely defined. These values of the permittivity are  and
and  for the bonding layer and the substrate, respectively. The permittivity of the GaAs layer could not be accurately determined in the same way due to its small thickness compared to the wavelength of THz radiation. Therefore, we approximate the permittivity of GaAs by that of a free electron gas described by the Drude model. This approximation has been proven to be valid for semiconductors at THz frequencies34. The frequency dependent complex permittivity
for the bonding layer and the substrate, respectively. The permittivity of the GaAs layer could not be accurately determined in the same way due to its small thickness compared to the wavelength of THz radiation. Therefore, we approximate the permittivity of GaAs by that of a free electron gas described by the Drude model. This approximation has been proven to be valid for semiconductors at THz frequencies34. The frequency dependent complex permittivity  resulting from the Drude model of free charge carriers is given by
resulting from the Drude model of free charge carriers is given by

where both electron-electron and electron-phonon interactions are taken into account. The relative high and low (DC) frequency dielectric constants are  and
and  , respectively. Moreover, the transverse optical phonon absorption is at νTO = 8.03 THz with a damping coefficient Γp = 0.072 THz. The plasma frequency of GaAs is given by
, respectively. Moreover, the transverse optical phonon absorption is at νTO = 8.03 THz with a damping coefficient Γp = 0.072 THz. The plasma frequency of GaAs is given by  where N is the carrier concentration per unit volume and meff = 0.063 me is the effective electron mass. The e-e collision rate is given by Γe = e/(meffμ), where μ is the carrier concentration dependent mobility, which can be approximated by the empirical relation43
where N is the carrier concentration per unit volume and meff = 0.063 me is the effective electron mass. The e-e collision rate is given by Γe = e/(meffμ), where μ is the carrier concentration dependent mobility, which can be approximated by the empirical relation43

Time-resolved THz time-domain spectroscopy
The measurements have been performed with a modified time-resolved THz time-domain spectrometer. With this pump-probe technique, a pulsed laser beam from an amplified oscillator (λ = 800 nm, repetition rate = 1 KHz, pulse duration = 100 fs) is split in three beams. One of the beams is used to generate THz radiation by optical rectification in a 0.5 mm thick ZnTe crystal. The THz pulse is collected by parabolic gold mirrors and weakly focused onto the sample. The beam size onto the sample has a FWHM of 2.5 mm. The transmitted THz radiation is focused onto a 1 mm thick ZnTe crystal. The THz field amplitude in this crystal is probed by the second optical beam, which detects changes in the refractive index of the ZnTe crystal induced by the THz pulse (electro-optical sampling). By controlling the time delay between the optical beam generating the THz pulse and the optical beam probing the THz field amplitude, it is possible to measure the THz amplitude transients. These transients can be Fourier transformed to obtain the amplitude or the power spectra. The third optical beam in the setup is used as an optical pump for the sample. Controlling the time delay between the optical pump and the THz pulse probing the sample allows an accurate investigation of carrier dymanics in photo-excited samples44.
FDTD simulations
The extinction and near fields were simulated using a commercial 3D - Finite Difference in Time Domain (FDTD) software. The simulated structures were chosen to be as close as possible to the experimental conditions, i.e., a multi-layered structure consisting of air - silicon oxide - bonding polymer - GaAs - air. The experimentally determined values of the permittivity of the bonding layer and the substrate were used for the simulations. An homogeneous carrier concentration was considered through the thickness of 1 μm of the GaAs layer. The illuminated rods were simulated by considering a rectangular region with rounded corners and a permittivity given by the Drude model. A graded illumination across the edges of the rods (see side graphs in Fig. 2(b)) was taken into account by considering consecutive shells with varying thickness of and a reduced carrier density as the shell dimensions is increased. The carrier density in the innermost region of the rod is N = 2 × 1018 cm−3, while the outermost shell has N = 5 × 1016 cm−3. The non-illuminated GaAs was assumed to have N = 5 × 1015 cm−3 to take into account the finite contrast between bright and dark pixels in the structured illumination. For the simulations we used a total field scattered field source, a perfectly matched layer as boundary of the simulated volume and a transmission monitor to determine the extinction. The simulated transmission was corrected by the rod filling fraction to compare quantitatively to the experiments.
References
Ebbesen, T. W., Lezec, H. J., Ghaemi, H. F., Thio, T. & Wolff, P. A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 391, 667–669 (1998).
Barnes, W. L., Dereux, A. & Ebbesen, T. W. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
schuller, J. A. et al. Plasmonics for extreme light concentration and manipulation. Nat. Mat. 9, 193–204 (2010).
Stockman, M. I., Kling, M. F., Kleineberg, U. & Krausz, F. Attosecond nanoplasmonic-field microscope. Nat. Phot. 1, 539–544 (2007).
Aeschlimann, M. et al. Adaptive subwavelength control of nano-optical fields. Nature 446, 301–304 (2007).
Volpe, G., Cherukulappurath, S., Parramon, R. J., Molina-Terriza, G. & Quidant, R. Controlling the Optical Near Field of Nanoantennas with Spatial Phase-Shaped Beams. Nano Lett. 9, 3608–3611 (2009).
Gjonaj, B. et al. Active spatial control of plasmonic fields. Nat. Phot. 5, 360–363 (2011).
Kao, T. S., Rogers, E. T. F., Ou, J. Y. & Zheludev, N. I. Digitally Addressable Focusing of Light into a Subwavelength Hot Spot. Nano Lett. 12, 2728–2731 (2012).
Perner, M. et al. Optically Induced Damping of the Surface Plasmon Resonance in Gold Colloids. Phys. Rev. Lett 78, 2192–2195 (1997).
Link, S. & El-Sayed, M. A. Spectral Properties and Relaxation Dynamics of Surface Plasmon Electronic Oscillations in Gold and Silver Nanodots and Nanorods. J. Phys. Chem B 103, 8410–8426 (1999).
Rotenberg, N., Betz, M. & van Driel, H. M. Ultrafast control of grating-assisted light coupling to surface plasmons. Opt. Lett. 33, 2137–2139 (2008).
Halté, V., Banabbas, A. & Bigot, J.-Y. Surface plasmon dynamics in arrays of subwavelength holes: the role of optical interband transitions. Opt. Express 16, 11611–11617 (2008).
MacDonald, K. F., Samson, Z. L., Stockman, M. I. & Zheludev, N. I. Ultrafast active plasmonics. Nat. Phot. 3, 55–58 (2009).
Temnov, V. V. et al. Femtosecond surface plasmon interferometry. Opt. Express 17, 8423–8432 (2009).
Dintinger, J., Robel, I., Kamat, P. V., Genet, C. & Ebbesen, T. W. Terahertz all-optical molecule-plasmon modulation. Adv. Mater. 18, 1645–1648 (2006).
Giannini, V., Berrier, A., Maier, S. A., Sánchez-Gil, J. A. & Gómez Rivas, J. Scattering efficiency and near field enhancement of active semiconductor plasmonic antennas at terahertz frequencies. Opt. Express 18, 2797–2807 (2010).
Allen, S. J., Tsui, D. C. & Logan, R. A. Observation of the Two-Dimensional Plasmon in Silicon Inversion Layers. Phys. Rev. Lett. 38, 980–983 (1977).
Gómez Rivas, J., Kuttge, M., Haring Bolivar, P., Kurz, H. & Sánchez-Gil, J. A. Propagation of surface plasmon polaritons on semiconductor gratings. Phys. Rev. Lett. 93, 256804 (2004).
Gómez Rivas, J. Terahertz: the art of confinement. Nat. Phot. 2, 137–138 (2008).
Neubrech, F. et al. Resonant Plasmonic and Vibrational Coupling in a Tailored Nanoantenna for Infrared Detection. Phys. Rev. Lett. 101, 157403 (2008).
Kundu, J., Le, F., Nordlander, P. & Halas, N. J. Surface enhanced infrared absorption (SEIRA) spectroscopy on nanoshell aggregate substrates. Chem. Phys. Lett. 452, 115119 (2008).
Schnell, M. et al. Controlling the near-field oscillations of loaded plasmonic nanoantennas. Nat. Phot. 3, 287–291 (2009).
Adatoa, R. et al. Ultra-sensitive vibrational spectroscopy of protein monolayers with plasmonic nanoantenna arrays. Proc. Nat. Acad. Sci. 106, 19227–19232 (2009).
Gómez Rivas, J., Kuttge, M., Kurz, H., Haring Bolivar, P. & Sánchez-Gil, J. A. Low-frequency active surface plasmon optics on semiconductors. Appl. Phys. Lett. 88, 082106 (2006).
Chen, H. T. et al. Active terahertz metamaterial devices. Nature 444, 597–600 (2006).
Chen, H. T. et al. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Phot. 2, 295–298 (2008).
Berrier, A., Ulbricht, R., Bonn, M. & Gómez Rivas, J. Ultrafast active control of localized surface plasmon resonances in silicon bowtie antennas. Opt. Express 18, 23226–23235 (2010).
Okada, T., Ooi, K., Nakata, Y. & Fujita, K. Direct creation of a photoinduced metallic structure and its optical properties in the terahertz frequency region. Opt. Lett. 10, 1719–1721 (2010).
Okada, T. & Tanaka, K. Photo-designed terahertz devices. Sci. Rep. 1, 121 (2011).
Chatzakis, I. et al. One- and two-dimensional photo-imprinted diffraction gratings for manipulating terahertz waves. Appl. Phys. Lett. 103, 043101 (2013).
Busch, S., Scherger, B., Scheller, M. & Koch, M. Optically controlled terahertz beam steering and imaging. Opt. Lett. 8, 1391–1392 (2012).
Rizza, C., Ciattoni, A., Columbo, L., Brambilla, M. & Prati, F. Terahertz optically tunable dielectric metamaterials without microfabrication. Opt. Lett. 38, 1307–1309 (2013).
Muskens, O. L., Giannini, V., Sánchez-Gil, J. A. & Gómez Rivas, J. Optical scattering resonances of single and coupled dimer plasmonic nanoantennas. Opt. Express 15, 17736–17746 (2007).
Beard, M. C., Turner, G. M. & Schmuttenmaer, C. A. Subpicosecond carrier dynamics in low-temperature grown GaAs as measured by time-resolved terahertz spectroscopy. J. Appl. Phys. 90, 5915–5923 (2001).
Novotny, L. Effective wavelength scaling for optical antennas. Phys. Rev. Lett. 98, 266802 (2007).
Cubukcu, E. & Capasso, F. Optical nanorod antennas as dispersive one-dimensional FabryProt resonators for surface plasmons. Appl. Phys. Lett. 95, 201101 (2009).
Giannini, V., Vecchi, G. & Gómez Rivas, J. Lighting up multipolar surface plasmon polaritons by collective resonances in arrays of nanoantennas. Phys. Rev. Lett. 105, 266801 (2010).
Padilla, W. J., Taylor, A. J., Highstrete, C., Lee, M. & Averitt, R. D. Dynamical electric and magnetic metamaterial response at terahertz frequencies. Phys. Rev. Lett. 96, 107401 (2006).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Gacemi, D., Mangeney, J., Colombelli, R. & Degiron, A. Subwavelength metallic waveguides as a tool for extreme confinement of THz surface waves. Sci. Rep. 3, 1369 (2013).
Voncken, M. M. A. J. et al. Etching AlAs with HF for epitaxial lift-off applications. J. Electrochem. Soc. 151, G346–G351 (2004).
Schermer, J. J. et al. Photon confinement in high-efficiency, thin-film IIIV solar cells obtained by epitaxial lift-off. Thin Sol. Films. 511–512, 645–653 (2006).
Hilsum, C. Simple empirical relationship between mobility and carrier concentration. Electron. Lett. 10, 259–260 (1974).
Ulbricht, R., Euan, H., Shan, J., Heinz, T. & Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 83, 543–586 (2011).
Acknowledgements
We are thankful to M.C. Schaafsma and J. Versluis for valuable discussions. This work has been supported by the ERC through grant no 259727 THZ-PLASMON and by the Netherlands Foundation for Fundamental Research on Matter (FOM) and the Netherlands Organisation for Scientific Research (NWO).
Author information
Authors and Affiliations
Contributions
G.G. did the measurements and simulations and partially wrote the manuscript, H.K.T. helped with the measurements, P.M., G.J.B. and J.J.S. fabricated the sample, J.G.R. conceived the experiment and partially wrote the manuscript. All the authors participated in the discussions and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Georgiou, G., Tyagi, H., Mulder, P. et al. Photo-generated THz antennas. Sci Rep 4, 3584 (2014). https://doi.org/10.1038/srep03584
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03584
This article is cited by
-
Metasurfaces for Terahertz Wavefront Modulation: a Review
Journal of Infrared, Millimeter, and Terahertz Waves (2020)
-
Excitation and propagation of surface plasmon polaritons on a non-structured surface with a permittivity gradient
Light: Science & Applications (2016)
-
Photo-generated metamaterials induce modulation of CW terahertz quantum cascade lasers
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.