Narrow Energy Gap between Triplet and Singlet Excited States of Sn²⁺ in Borate Glass

Abstract

Transparent inorganic luminescent materials have attracted considerable scientific and industrial attention recently because of their high chemical durability and formability. However, photoluminescence dynamics of ns²-type ions in oxide glasses has not been well examined, even though they can exhibit high quantum efficiency. We report on the emission property of Sn²⁺-doped strontium borate glasses. Photoluminescence dynamics studies show that the peak energy of the emission spectrum changes with time because of site distribution of emission centre in glass. It is also found that the emission decay of the present glass consists of two processes: a faster S₁-S₀ transition and a slower T₁-S₀ relaxation and also that the energy difference between T₁ and S₁ states was found to be much smaller than that of (Sn, Sr)B₆O₁₀ crystals. We emphasize that the narrow energy gap between the S₁ and T₁ states provides the glass phosphor a high quantum efficiency, comparable to commercial crystalline phosphors.

Introduction

Nowadays, various types of rare earth (RE)-doped phosphors are being actively developed worldwide for applications in light emitting diodes (LEDs)¹, displays², scintillators³, persistent luminescence⁴ and solid-state laser materials⁵. For example, phosphors for white LEDs have been enthusiastically examined^6,7,8. These LEDs are expected to replace conventional white fluorescent lamps in the future because of their several advantages such as absence of Hg vapour, long life-span and low power consumption. Although deep-UV LEDs are not currently available commercially, recent developments in the field of LEDs clearly suggest a possibility of their realization in the near future^9,10,11. However, the organic sealant for most types of powdered phosphors is damaged by high-power and/or high-energy excitation light sources. Consequently, it is expected that a monolithic material possessing high durability as well as good emission property will be required for future applications. Therefore, inorganic glasses exhibiting emission property are one of the practical phosphor candidates.

Investigation into the emission property of amorphous glasses has been mainly limited to RE-containing glasses¹². This is not only because the analysis of RE cations whose emission is almost independent of the coordination state is relatively simple compared to other emission centres, but also because glass materials possessing random networks are thought to be unsuitable for a precise analysis of their luminescent property. In addition, oxide glasses have not attracted attention as phosphor candidates, despite possessing good formability and wide transparent wavelength region, because it is believed that such glasses exhibit low emission intensity. Therefore, the local structure of the emission centre in the amorphous glass has not been previously discussed, although its site distribution can vary.

Our group has focused on the ns²-type cations (n ≧ 4) such as Sn²⁺, Sb³⁺, Hg⁰, Tl⁺ and Pb²⁺ that give strong photoluminescence (PL) because of the parity allowed transition^13,14. Because these types of emission centres possess electrons in the outermost shell in both the ground state (ns²) and the excited state (ns¹np¹), the emission spectrum is strongly affected by the coordination field. Therefore, it can be said that the amorphous glass, in which site distribution is much broader than that in a crystal, is one of the most fascinating solid-state host materials for an emission centre. Recently, we reported the emission property of the SnO-ZnO-P₂O₅ glass^{15,16,17,18,19,20}. This glass showed blue light emission with high quantum efficiency (QE) caused by deep-UV irradiation. The emission is brought about by Sn²⁺, which is the most common ns²-type centre¹³. It is notable that the transparent glass containing no RE cations shows intense UV-excited emission that is comparable to a crystal phosphor such as MgWO₄. Furthermore, the SnO-ZnO-P₂O₅ glass shows the highest efficiency among the glass materials that have no RE cations¹⁵. We have also demonstrated white light emission from the MnO-doped SnO-ZnO-P₂O₅ glass whose QE is comparable to MgWO₄^16,17. Thus, the emission consisting of broad bands can be tailored by the addition of another emission centre such as Mn²⁺ or by changing the local coordination field (i.e., the chemical composition of the host glass) of the Sn²⁺ centre. Recently, we have also reported that the emission of the Sn²⁺ centre does not reflect the average (macroscopic) basicity of the glass; instead, it reflects the local basicity of the emission centre²⁰. The result indicates that macroscopic randomness is not important for attaining high QE and that amorphous materials can exhibit high conversion efficiency comparable to that of crystalline phosphors by controlling the microscopic coordination state.

In the present study, we focus on a Sn-doped borate glass. Because the melting temperature required for fabricating borate glasses is generally lower than that required for conventional oxide glasses, partial oxidation of Sn²⁺ in the glass melt is expected, which results in a decrease in the emission efficiency. On the other hand, it is worthwhile to examine the PL of the Sn²⁺ emission centre in a random matrix instead of in phosphate glasses, because different host glasses provide the Sn²⁺ emission centre with different coordination fields. Neither the coordination state nor the emission mechanism of Sn²⁺ in a borate glass has yet been investigated; therefore, their investigation is attractive from scientific and industrial viewpoints. Because the Sn-doped SrB₆O₁₀ crystal is known to show emission by UV excitation^21,22, it is expected that the Sn-doped borate glass also possesses a comparable emission property. For comparison, the chemical composition of the host glass was selected as 25.0SrO-75.0B₂O₃, which is equivalent to the stoichiometric composition of SrB₆O₁₀. Examining the effect of the randomness of the oxide matrix on the emission property of the Sn²⁺ emission centre is also meaningful from the viewpoint of the local structure in the glass matrix.

Results

Thermal property of SnO-doped strontium borate glasses

Transparent xSnO-(25.0-x)SrO-75.0B₂O₃ glasses were obtained in the region 0 ≤ x ≤ 1.8. The glass became translucent when x was increased to 1.9 because of the precipitation of SnO₂. T_g of the nondoped 25SrO-75B₂O₃ glass was 610°C, which is approximately 200°C higher than previous phosphate glasses¹⁵ and decreased with increasing amount of SnO.

PL-PL excitation (PLE) spectra of SnO-doped strontium borate glasses

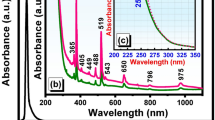
Figure 1 shows normalized PL-PLE spectra of xSnO-(25.0-x)SrO-75.0B₂O₃ glasses. Optical absorption spectra of these glasses are also shown. The PLE spectra were measured at the peak photon energy of each PL spectrum, whereas the PL spectra were measured by excitation at the peak energy of each PLE spectrum. The peak energy of the asymmetric broad emission slightly red-shifts with an increasing amount of SnO, although the peak width is almost unchanged. Because the SnO-free 25.0SrO-75.0B₂O₅ glass (x = 0) exhibiting the absorption edge at much higher photon energy (over 6 eV) shows no emission, it is clear that not only the emission band but also the observed absorption edge of the Sn-doped glass originates from the Sn²⁺ species. The main excitation band position locates in the vicinity of the optical absorption edge, which was also observed in the SnO-doped zinc phosphate glass system^15,19. It is also found that the PLE spectra apparently consist of two bands; among them, the lower energy band strongly correlates with the optical absorption edge¹⁹. It was reported that the twofold-coordinated Sn in SiO₂ shows two emission bands: α-band [singlet (S₁) - singlet (S₀), ~4.1 eV] and β-band [triplet (T₁) - singlet (S₀), ~3.1 eV]²³. Although the T₁ state consists of ³P₀, ³P₁ and ³P₂¹³, we use “T₁” in the present paper, because the actual coordination number of Sn²⁺ to determine the transition probability has not yet been clarified. If we consider the origin of the emission based on the photon energy, the emission can be mainly attributed to the T₁-S₀ relaxation. The emission intensity has a maximum at composition x = 0.2, which is much smaller compared to that of a SnO-doped zinc phosphate glass system¹⁹. It is because overlapping of PL and PLE bands in the present borate system takes place even though SnO concentration was less than 1.0 mol% (see Fig. 1). The overlapping of PL and PLE bands induces concentration quenching to decrease emission intensity. On the other hand, the PLE band becomes broader with an increasing amount of SnO, while the peak energy is almost unchanged. Therefore, the absorption spectra and PLE bands of several Sn-containing glasses were examined to clarify in detail the correlation between the SnO amount and the PLE bands.

Figure 1

Concentration dependence of PL, PLE and optical absorption spectra of xSnO-(25-x)SrO-75B₂O₃ glasses.

PL and PLE spectra (solid line) are normalized. Absorption spectra (dashed line) indicate that strong absorption band originating in Sn²⁺ correlates with emission.

Figure 2(a) shows a PLE spectrum of the 1.5SnO-23.5SrO-75B₂O₃ glass together with the two bands deconvoluted using Gaussian functions: the higher energy excitation band A at 4.9 eV and the lower energy excitation band B at 4.2 eV. Figure 2 (b) shows the peak area ratio B/(A + B) and the peak energy of A and B bands as a function of SnO amount. With increasing SnO amount, the peak area ratio of the B band increases and the peak energy red-shifts. Note that the peak energy of the B band closely corresponds to the optical absorption edge estimated from the absorption spectra. It was reported that the twofold-coordinated Sn²⁺ species in SiO₂ exhibits several excitation bands and the photon energy for the S₀-S₁ excitation is calculated as 4.9 eV²³. Comparing this value with the present two values: 4.2 eV and 4.9 eV, it is expected that the excitation band A, whose peak position is independent of the SnO concentration, arises because of the S₀-S₁ excitation process of the twofold-coordinated Sn²⁺ species.

Figure 2

Concentration dependence of PLE spectra of xSnO-(25-x)SrO-75B₂O₃ glasses.

(a) PLE spectrum (emission at 3.13 eV) of 1.5SnO-23.5SrO-75B₂O₃ glass together with deconvoluted bands: higher energy band A and lower energy band B. (b) Peak position and area of B band as a function of SnO amount in PLE spectra of xSnO-(25-x)SrO-75B₂O₃ glasses.

Figure 3 shows the PL-PLE contour plots of the xSnO-(25.0-x)SrO-75.0B₂O₃ glasses: (a) x = 0.1, (b) 0.5 and (c) 1.0, using an intensity axis on a linear scale. The contour plot of the (Sn_0.02Sr_0.98) B₆O₁₀ crystal (d) is also shown for comparison. The emission intensity decreases with increasing amount of SnO, which is clearly because of the concentration quenching. These figures indicate that the higher the excitation energy, the higher the emission peak energy. In other words, the higher the S₁ energy level, the higher the T₁ level. Although a weak S₀-T₁ excitation band is observed at 3.9 eV in the (Sn_0.02Sr_0.98)B₆O₁₀ crystal²¹, indicated by the dashed circle in Fig. 3(d), no such excitation band is observed in the corresponding glasses. It is also obvious from Figs. 3(b) and (d) that both the excitation and emission bands are much broader in the glasses than in the corresponding crystal.

Figure 3

PL-PLE contour plots of xSnO-(25-x)SrO-75B₂O₃ glasses.

(a) x = 0.1, (b) x = 0.5 and (c) x = 1.0. Contour plot of (Sn_0.02Sr_0.98)B₆O₁₀ crystal (d) is also shown for comparison. Dashed circle in (d) shows weak excitation band owing to S₀-T₁ excitation²¹.

Photoluminescence dynamics of SnO-doped strontium borate glasses

The emission decay curves monitored at 2.95 eV for the xSnO-(25.0-x)SrO-75.0B₂O₃ glasses and the (Sn_0.02Sr_0.98)B₆O₁₀ crystal are shown in Fig. 4, where the samples were irradiated using UV light of 4.43 eV. The decay curves consist of two components: a faster component (lifetime, τ′_1/e, of nanoseconds) and a slower component (τ″_1/e of microseconds). From the decay curves of the glasses, τ″_1/e was estimated as 7.4 ~ 5.6 μs, which decreases with increasing SnO amount as shown in Table 1. It seems that the emission decay of the microsecond order can be expressed using a single exponential curve and the emission has its origin in the Sn²⁺ emission centre. The decrease of decay constants suggests the concentration quenching occurs as shown in Fig. 1. Because the lifetime of the glasses is longer than that of the crystal (~4.0 μs)²¹, we have speculated that the structural disorder of the host material affects the lifetime of the Sn²⁺ emission centre. However, the faster decay was not observed in the SnO-ZnO-P₂O₅ glass system, which also showed the emission of Sn^2+16,17,19. Therefore, it is expected that relaxation of the nanosecond order in the borate glass originates from the different coordination field of the Sn²⁺ centre in the phosphate glasses. As mentioned above, if we consider the origin of the emission based on the photon energy, we will find that the emission can be mainly attributed to the T₁-S₀ relaxation. However, when the presence of the faster relaxation is taken into account, whose decay time is shorter than 10 ns, it is expected that both the S₁-S₀ and T₁-S₀ relaxations exist. It turns out that the peak energy of the S₁-S₀ relaxation (~3.4 eV) in the present glass is much lower than that in the SiO₂ glass (~4.1 eV).

Table 1 Photoluminescent properties of the xSnO-(25-x)SrO-75B₂O₃ glasses and (Sn_0.02Sr_0.98)B₆O₁₀ crystal. The errors of QE measurement and decay constants were ±2% and ±0.2 μs, respectively

Figure 4

Intensity decay curves of xSnO-(25-x)SrO-75B₂O₃ glasses and (Sn_0.02Sr_0.98)B₆O₁₀ crystal.

Decays of Sn²⁺ emission at 2.95 eV were measured with excitation energy 4.43 eV.

Photoluminescence dynamics analysis using streak images

In order to confirm the existence of the faster emission decay, photoluminescence dynamics at room temperature was also evaluated using a streak camera and a monochromater. Figure 5a and 5b show the streak images of the 1.0SnO-24.0SrO-75.0B₂O₃ glass and (Sn_0.02Sr_0.98)B₆O₁₀ crystal, respectively. The vertical and horizontal axes show the timescale and photon energy, respectively. It is notable that timescale of the borate glass is nanosecond whereas that of crystal is microsecond. The image clearly shows the existence of fast decay in borate glass with a lifetime of less than 10 ns, which is different from conventional decay constant of Sn²⁺ centre in crystal with T₁-S₀ relaxation. The emission peaks of two materials are ~3.4 eV (glass) and 2.9 eV (crystal), suggesting these concerning energy levels are different. It also suggests that the emission peak energy of the glass slightly red-shifts, which is different from (Sn_0.02Sr_0.98)B₆O₁₀ crystal (see supplemental Fig. 1). Figure 5c shows the correlation between the emission peak energy and the time elapse of the 1.0SnO-24.0SrO-75.0B₂O₃ glass. The emission peak energy shifts toward lower energy with increasing time elapse, suggesting that the lower the emission peak energy, the longer the lifetime. Although the peak energy of the 1.0SnO-24.0SrO-75.0B₂O₃ glass is slightly higher than that of other glass systems, their time evolution is comparable. Because the internal QEs of the obtained glasses were at least 55% and that of the 0.2SnO-24.8SrO-75B₂O₃ glass was 81%, the main relaxation process is surely due to the photoluminescent decay. Because the Sn-free glass does not show such emission, we have attributed the observed emission decay of the nanoscale order to the S₁-S₀ relaxation of the Sn²⁺ centre, which has not been observed for phosphate glass systems. It is notable that internal QEs of the obtained glasses are higher than that of (Sn_0.02Sr_0.98)B₆O₁₀ crystal. This is also an advantage of the present Sn²⁺-doped glass phosphor.

Figure 5

Time-dependent emission property of SnO-SrO-B₂O₃ glasses and (Sn_0.02Sr_0.98)B₆O₁₀ crystal.

Streak images of 1.0SnO-24.0SrO-75B₂O₃ glass (a) and (Sn_0.02Sr_0.98)B₆O₁₀ crystal (b) excited by photon energy 4.86 eV. (c) Time-dependence of emission peak energy of xSnO-(25-x)SrO-75B₂O₃ glasses. Radiative relaxation of nanosecond order indicates relaxation from S₁ excitation state.

Valence states of Tin in strontium borate glasses and crystal

Because the valence state of Sn is easily varied with the the preparation conditions, such as Sn concentration, preparation atmosphere and basicity of the host glass, it is important to examine the valence state of Sn in the matrix. Since Sr cation absorbs γ-ray of Sn, however, it is difficult to estimate Sn²⁺/Sn⁴⁺ ratio in these materials from the ^119mSn Mössbauer spectroscopy. Therefore, X-ray absorption fine structure (XAFS) measurement is only one approach for the evaluation. Figure 6 shows Sn K-edge XANES spectra of several xSnO-(25.0-x)SrO-75.0B₂O₃ glasses (x = 0.5, 1.0 and 1.5) along with those of SnO and (Sn_0.02Sr_0.98)B₆O₁₀ crystal. Because a higher absorption edge indicates a higher oxidation state of the cation, we take absorption edge energy, E₀, to be the energy at the zero-crossing of the 2nd derivative. The Sn K-edge energies of xSnO-(25.0-x)SrO-75.0B₂O₃ glasses are similar to that of SnO. Using each E₀ value, |Δ(E₀(SnO)-E₀(glass))| is calculated to be less than 0.6 eV. Considering the resolution of the measurement (ΔE/E ~ 6 × 10⁻⁵), we assume that this difference (less than 1.75 eV) is insignificant. Thus, Sn K-edge XAFS supports the hypothesis that the percentage of Sn²⁺ to total Sn in xSnO-(25.0-x)SrO-75.0B₂O₃ glass is nearly 100%.

Figure 6

Sn K-edge XANES spectra of the xSnO-(25-x)SrO-75B₂O₃ glasses along with those of SnO and (Sn_0.02Sr_0.98)B₆O₁₀ crystal for reference.

| The Sn K-edge energies of xSnO-(25.0-x)SrO-75.0B₂O₃ glasses were similar to that of SnO.

Discussion

RE-free emitting material is attractive not only from the viewpoint of the uneven distribution of RE on earth but also from the unique property²⁴. The present results clearly suggest that Sn²⁺-containing glasses can be used as alternative inorganic phosphors that exhibit transparency in the visible region as well as a high QE. Although there are several reports on the luminescent property of Sn-containing glasses^{25,26,27,28,29}, the reported quantum efficiencies were lower than that of our results. This is because these previous reports lack control of the Sn²⁺ cation that can give high QE because of the parity allowed transition. Because Sn²⁺ is a very sensitive and metastable species at higher temperatures, it is often reported that Sn²⁺ in a glass melt is easily oxidized during the melt in air condition. However, Sn K-edge XAFS measurement suggests that most of tin species in the present borate glass is Sn²⁺ that affects the emission property. We have confirmed that PLE spectrum of xSnO-(25.0-x)SrO-75.0B₂O₃ glasses melted in Ar atmosphere is similar to that of the one melted in air (see supplemental Fig. 2). It confirms that (1) percentage of Sn²⁺ to total Sn in xSnO-(25.0-x)SrO-75.0B₂O₃ glass is nearly 100%, (2) both excitation bands originate from Sn²⁺ centres. It was reported that there is an equilibrium reaction between Sn²⁺/Sn⁴⁺ and BO₄⁴⁻/BO₃³⁻ as shown in Eq. (1),

Since¹¹B MAS NMR spectrum of xSnO-(25.0-x)SrO-75.0B₂O₃ glass (see supplemental Fig. 3) consists of both BO₄⁴⁻ and BO₃³⁻ units, it is expected that Sn²⁺ species preferentially generated in the present melting condition (at 1100°C for 20 min) even though melting was performed in air. The effect of the equilibrium reaction on the valence state of tin will be clarified in a separated paper by comparison with the glass melted in Ar and that of the one melted in air.

As shown in Figs. 1–2, the excited state of Sn²⁺ in borate glasses consists of two bands. Although two excitation bands attributed to the Sn²⁺ emission centre in glass materials have been reported^19,20,21, there are conflicting assignments of the excitation bands. Considering the previous finding that the Sn²⁺ centre in a silica glass with the C_2v symmetry shows the S₁ band at 4.9 eV²¹ and the present finding of the high internal QEs (at least 55%), we assume that there are two different Sn²⁺ emission centres that take different coordinate states¹⁷. According to a previous report concerning Sn²⁺ in zinc phosphate glasses¹⁷, we call the higher energy band (A) the S₁ band and the lower band (B) the S₁′ band. The S₁ band at 4.8–4.9 eV, whose energy is comparable to the previous value²¹, is almost unchanged, whereas the lower band S₁′ red-shifts with an increasing amount of SnO, as shown in Fig. 2. The emergence of the S₁′ band is also observed in the PL-PLE contour mappings (Fig. 3), in which the lower excitation band is observed in the glass containing a high amount of SnO. Therefore, it is suggested that the S₁′ band originates in a local structure different from the one that yields the S₁ band (two coordinated Sn²⁺ centre with C_2v symmetry) that occurs at low Sn²⁺ concentration. However, the peak area of the S₁′ band in the borate glass is much smaller than that in the phosphate glass containing the same SnO concentration¹⁷. Because the network randomness of phosphate glasses is higher than that of borate glasses, it is expected that not only a high ionic network but also the network flexibility are responsible for high SnO concentration and the existence of the S₁′ state. Although the actual coordination of Sn²⁺ at the S₁′ state in the borate glass is unknown, we believe that the S₁′ state is characteristic of the glass phosphor exhibiting high QE.

In the present study, we assume that emission at the microsecond scale originates during the relaxation from the T₁ state, although the actual spin state has not been measured. Similarly, based on the timescale, it is assumed that the emission occurs from the S₁ state. We have recently reported that the emission of Sn²⁺ is affected by the local coordination field¹⁸ and not by the average basicity of glasses. It is expected that a nonuniform distribution of the Sn²⁺ emission centre in the glass causes a wide distribution of the excitation energy and lifetime. An expected large distribution of the S₁ state of the Sn²⁺ emission centre in the glass is actually observed in the PL-PLE contour mapping and the time-dependent emission decay curves. In particular, the streak images, with a lifetime of nanoseconds, show that the time-integrated PL spectra consist of asymmetric emission exhibiting nonexponential decay at the nanosecond order. Because radiative relaxation at the nanosecond order has not been reported in Sn²⁺-doped crystals or in Sn²⁺-doped phosphate glasses, we emphasize that the observed relaxation depends on the borate glass system. In addition, it is notable that emission peak energy of S₁–S₀ relaxation is close to that of T₁–S₀ relaxation. Although it is expected that the difference originates from both the symmetry and basicity of local coordination field of Sn²⁺ centre, it has not been clarified yet. Further study is needed for understanding the basic science to improve the performance.

Based on these results, we discuss the emission mechanism of the xSnO-(25.0-x)SrO-75.0B₂O₃ glass. Figure 7 shows plausible energy schemes for the photoluminescence process of Sn²⁺ in the (Sn_0.02Sr_0.98)B₆O₁₀ crystal¹⁹ (a), Sn-doped SiO₂ glass²¹ (b) and 0.5SnO-24.5SrO-75.0B₂O₃ glass (c). In the case of the (Sn_0.02Sr_0.98)B₆O₁₀ crystal, photon energies for the S₀–S₁ and S₀–T₁ excitations are 4.8 and 3.9 eV, respectively. The observed emission at 2.9 eV is attributed to the T₁–S₀ relaxation. However, the photon energy for the S₀–S₁ excitation in the two glasses is 4.9 eV, which is slightly higher than that in the corresponding crystal. In the glass material, there are two decay processes: one corresponding to a faster relaxation from the S₁ state and the other corresponding to a slower one from the T₁ state. Although the emission energy from the T₁ state of silica glass is similar to that of the present borate glass, the emission energy from the S₁ state of the former is higher than that of the latter. It is easily understood that the smaller the energy difference between the S₁ and T₁ states, the more effective the intersystem crossing will be to prevent nonradiative transition. Therefore, it is expected that the high QE of the present glass, which is comparable to the crystalline phosphor, is attained by the unique energy scheme shown in Figure 7c. Most previous works on photoluminescence of ns²-type emission centre were performed in alkali halide systems^30,31,32. Although it has been thought that ns²-type ion takes O_h symmetry in both halides and oxide, it is natural that the emission centre possessing the lone pair electrons exhibits more disordered symmetry in glass (random) materials. We have, therefore, emphasized that ns²-type centre in random materials possessing unique emission property will open up an application field for emitting materials.

Figure 7

Plausible energy scheme for photoluminescence process of Sn²⁺ emission centre.

(a) (Sn_0.02Sr_0.98)B₆O₁₀ crystal²¹, (b) Sn²⁺-doped silica glass²³ and (c) 0.5SnO-24.5SrO-75B₂O₃ glass. Solid lines and dashed lines indicate radiative and nonradiative transitions, respectively. Photon energies of each excitation (blue) and relaxation (red) processes are shown.

In summary, we have demonstrated the UV-excited light emission property of Sn²⁺-doped strontium borate glasses. Two excitation bands emerged depending on the amount of SnO, where the lower energy band strongly correlates with the optical absorption edge. The broad emission of the glass is caused by the S₁-S₀ and T₁-S₀ relaxation processes of Sn²⁺ centre. The randomness of the amorphous matrix makes the emission decay duration longer compared with the corresponding crystal. It is notable that the energy difference between the S₁ and T₁ states is much narrower in the glass than the corresponding crystal, which may give the glass phosphor a high QE, comparable to the commercial crystalline phosphor. The present paper demonstrates a possibility of unique emission property of ns²-type centre in a random matrix, which will be different from the conventional emission system in halide crystals.

Methods

Preparation of SnO-doped strontium borate glass

The xSnO-(25.0-x)SrO-75.0B₂O₃ glasses were prepared according to a conventional melt-quenching method using a platinum crucible. Batches consisting of SnO (99.5%), SrCO₃ (99.9%) and B₂O₃ (99.9%) were mixed and melted at 1100°C for 20 min. The glass melt was quenched on a stainless steel plate maintained at 200°C and then annealed at the glass transition temperature, T_g, as measured by the differential thermal analysis (DTA), for 1 h. After cutting (10 mm × 10 mm × 1 mm), the glass samples were optically polished with an aqueous diamond slurry.

Analysis methods. The absorption spectra were measured using a U3500 UV-vis-NIR spectrophotometer (Hitachi, Japan). The photoluminescence (PL) and PL excitation (PLE) spectra were measured at room temperature using an 850 fluorescence spectrophotometer (Hitachi, Japan). Band pass filters were used for the excitation (5 nm) and the emission (3 nm) for PL measurements. The emission decay at room temperature was measured using a Quantaurus-Tau (Hamamatsu Photonics, Japan). The excitation light source used was an LED operated at photon energy 4.43 eV and frequency 10 kHz. The PL dynamics was also evaluated using a streak camera and a monochromater. The light source used for photoexcitation was an optical parametric amplifier system based on a regenerative amplified mode-locked Ti:sapphire laser (Spectra Physics, USA) with a pulse duration of 150 fs and a repetition rate of 1 kHz. The photon energy was 4.96 eV, which corresponded to the peak energy of the PLE spectra. The Sn K-edge (29.3 keV) XAFS spectra were measured at BL01B1 of SPring-8 (Hyogo, Japan). The storage ring energy was operated at 8 GeV with a typical current of 100 mA. The measurements were carried out using a Si (311) double crystal monochromator in the transmission mode (Quick Scan method) at r.t.

Preparation of SnO-doped strontium borate crystal. For comparison, a (Sn_0.02Sr_0.98)B₆O₁₀ crystal was prepared by sintering. According to a previous report²¹, the starting materials of SnO, SrCO₃ and B₂O₃ were mixed and heat-treated twice at 800°C in a N₂ atmosphere. A pellet of the sintered (Sn_0.02Sr_0.98)B₆O₁₀ crystal (10 mm in diameter) was used for the measurements.