Abstract
Graphene was the first material predicted to realize a topological insulator (TI), but unfortunately the gap is unobservably small due to carbon's weak spin-orbital coupling (SOC). Based on first-principles calculations, we propose a stable sp-sp2 hybrid carbon network as a graphene analog whose electronic band structures in proximity of the Fermi level are characterized by Dirac cones. We demonstrate that this unique carbon framework has topologically nontrivial electronic structures with the Z2 topological invariant of v = 1 which is quite promising for hosting the quantum spin Hall effect (QSHE) in an experimentally accessible low temperature regime (<7 K). This provides a viable approach for searching for new TIs in 2D carbon allotropes.
Similar content being viewed by others
Introduction
Topological insulators (TIs) comprising of a class of remarkably spin-orbital-coupled nonmagnetic materials are insulating in the bulk but on the boundary they have gapless edge or surface states that are topologically protected by time reversal symmetry1,2,3. The exotic phenomena of these systems, including Majorana fermions4,5, charge fractionalization6 and novel magnetoelectric7,8,9, are quite promising for the uses of quantum computing2 and spintronic devices10. Two-dimensional (2D) TIs are ideally suitable for such applications due to robustness of conducting edge states from backscattering and graphene was the first material predicted to realize a TI1, in which the spin-orbital coupling (SOC) opens a band gap at the Dirac points (K and K/). The quantum spin Hall effect (QSHE), a new quantum state of matter with a nontrivial topological property, was expected to be observed in graphene, where the time reversal invariant electronic state with a bulk electronic band gap will support the transport of charge and spin in gapless edge state. Subsequent works, however, indicated that the gap is unobservavbly small (~10−3 meV) and the QSHE in graphene can occur only at an unrealistically low temperature, because the SOC is rather weak, which is in fact a second order process for graphene11,12,13,14. Further theoretical works suggest that the SOC gap of graphene can be dramatically enhanced to detectable values by dilute concentrations of 3d or 5d transition metal adatoms15,16,17,18,19, which can host a quantum spin Hall state or a quantum anomalous Hall state. This was attributed to the hybridization of graphene with impurity bands arising from heavy adatoms possessing partially filled d shells, as well as the interplay between proximity-induced magnetization and Rashba SOC. The quantum spin Hall states in some metal-organic frameworks with remarkable SOC has also been proposed based on first-principles20,21,22,23,24. However, if the QSHE in 2D carbon materials without dopants can occur at experimentally accessible low temperature remains doubtful.
Recent works show that carbon has abundant 2D allotropes beyond graphene. The most representative allotropes are the so-called graphynes, which are built from triple- and double-bonded units of carbon atoms25,26,27,28. Many graphynes can be assumed to be chemically stable, even though they are less favorable in formation energy than graphene due to the presence of sp-hybridized carbons. Indeed, finite building blocks and cutouts have already been synthesized and first steps towards the preparation of extended graphynes have been proposed and developed29,30,31,32,33,34,35. The presence of acetylenic bonds associated with sp-hybridized carbon atoms in these 2D frameworks introduces a rich variation in electronic and optical properties. Considerable efforts have been devoted to the electronic structures of graphynes26,28,36,37,38,39,40,41,42,43. Both γ-graphyne and the already-synthesized graphdiyne film are semiconducting with a moderate band gap of about 1.1 eV42,43. Interestingly, there exists a special class of graphynes associated with Dirac-cone-characterized electronic band structures in proximity of Fermi level. Up to now, this special class includes α-graphyne, β-graphyne and 6,6,12-graphyne belonging to different lattices28. Unlike graphene, the Dirac cones are not located at the K or K/ point but on the lines from Γ to M for the hexagonal β-graphyne. Rectangular 6,6,12-graphyne lattice, however, has two self-doped nonequivalent distorted Dirac cones28. In a sense, honeycomb α-graphyne is by far an ideal analog of graphene in both the shape and positions of Dirac cones, but it is energetically most unstable among the graphynes. The abundant 2D carbon allotropes with versatile electronic properties offer candidate materials for hosting QSHE superior to graphene, unfortunately, such possibility has never been considered, partly due to the weak SOC revealed in graphene.
In this work, from first-principles calculations within density-functional theory (DFT), we propose a novel 2D carbon allotrope, named as δ-graphyne (Figure 1(a)), which has higher energetic favorability compared with most of the graphynes including α- and β-graphynes, as well as the already-synthesized graphdiyne. Like graphene, the band structure of δ-graphyne in proximity of the Fermi level can be characterized by Dirac cones at the K and K/ points of the Brillouin zone (BZ), except that the slope of the Dirac cones (Fermi velocity) is only 56% of that of graphene. Combined with a tight-binding method, we demonstrate that δ-graphyne has topologically nontrivial electronic structures with a Z2 topological invariant of v = 1. The band gap opened up at the Dirac points of δ-graphyne due to the SOC for the π orbital is about 0.59 meV, which can host the QSHE in an experimentally accessible low temperature regime (<7 K). This offers a viable approach for searching new TIs in 2D carbon allotropes.
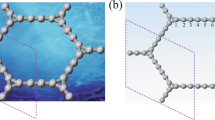
(a) Schematic representation of honeycomb lattice of δ-graphyne with a unit cell indicated by the dashed lines. The two basis vectors are represented by a1 and a2. Carbon atoms in difference chemical environments (C1, C2 and C3) are indicated by the balls in different colors. (b) Phonon spectrum of δ-graphyne along the high symmetric points in the BZ.
Results
Generally, the frameworks of graphynes comprise of sp-hybridized carbon atoms accompanied by acetylenic bonds beside sp2-hybridized carbon atoms, but the ratios of the sp-hybridized carbon atoms and the arrangements of the acetylenic bonds differ significantly for different allotropes. The honeycomb framework of δ-graphyne is plotted in Figure 1(a). We classify the carbons atoms of δ-graphyne into three types: (1) sp2-hybridized carbon atoms at the hexagons (denoted as C1 hereafter); (2) sp-hybridized carbon atoms forming the acetylenic bonds (C2); and (3) sp2-hybridized carbon atoms joint to three sp-hybridized carbon atoms (C3). The length of the covalent bond between C1 atoms is 1.437 Å, slightly longer than that in graphene,1.420 Å. The length of the acetylenic bond (C2-C2) is about 1.229 Å. The lengths of the bonds between C1 and C2 and that between C2 and C3 are 1.389 Å and 1.395 Å, respectively, both of which are shorter than the C1-C1 covalent bond, due to the stabilization effect of the triple bonds. All the atoms are on the same plane without any buckling. The unit cell contains 20 carbon atoms and the optimized lattice constant (the length of lattice vectors) is 9.440 Å. The ratio of sp-hybridized carbon atoms is 0.6, lower than that of α-graphyne (0.75), due the existence of carbon hexagons.
To compare the energetic stability of δ-graphyne with other graphynes, we plotted their formation energies with respect to graphene in Fig. 2. The datum of graphdiyne monolayer whose multi-layered counterpart (graphdiyne film) has been fabricated in recent experiments35 is presented as a reference point (represented by the dashed line). The graphynes with formation energy lower than that of graphdiyne monolayer are expected to be plausible. From this figure, we can see the following features: (1) These graphynes are energetically less favorable than graphene, due to the presence of sp-hybridized carbon atoms, however, δ-graphyne, 6,6,12-graphyne and γ-graphyne are more stable in energy than the reference point of graphdiyne monolayer. Especially, δ-graphyne is energetically more favorable than the reference point by about 0.022 eV/atom. (2) The formation energy (Eform) of these graphynes varies linearly with respect to the sp-hybridized carbon atoms ratio x and can be fitted using the formula: Eform = kx, with k = 1.25 eV/atom, as indicated by the solid line in Fig. 2. This linear relationship can be easily understood by supposing that the energy increase of graphynes with respect to graphene is due to the sp-hybridized atoms. In this case, the value of k represents the energy increase of a sp-hybridized atom relative to the sp2-hybridized carbon atom in graphene. This empirical formula is useful for evaluating the energetic priority of graphynes simply from the sp-hybridized carbon atom ratio, i.e., a smaller x corresponds to higher energetic favorability. Noting that δ-graphyne is not energetically most stable among the graphynes under study (less stable than 6,6,12-graphyne and γ-graphyne), however, γ-graphyne is semiconducting and 6,6,12-graphyne has two self-doped nonequivalent distorted Dirac cones both of which are unsuitable for hosting QSHE.
The formation energies (Eform) of some representative graphyne allotropes (α-,β-,γ-,δ- and 6,6,12-graphynes, as shown in the inset of this figure) with respect to graphene as a function of sp-hybridized carbon atom ratio, x.
The data are fitted by the formula: Eform = 1.25x, as indicated by the solid line. The formation energy of the already-synthesized graphdiyne, 0.772 eV/atom, is indicated by the dash line.
The kinetic stability of the δ-graphyne is also confirmed from a vibrational analysis of the phonon spectrum calculated from first-principles. We didn't find the modes with imaginary frequencies in the phonon spectrum along the highly-symmetric points of BZ as shown in Fig. 1(b). We also heated a large supercell (4 × 4) of δ-graphyne at 500 K for 1.0 ps by using the Nose thermostat to check the thermal stability. No obvious collapse tendency of the framework was found at this time scale. These results imply the stability and plausibility of the δ-graphyne from other points.
The electronic structures of the δ-graphyne are then calculated. The band lines along the highly-symmetric point of BZ are plotted in Fig. 3 (a). There are six points (three equivalent K and three equivalent K/) in the BZ where conduction and valence bands meet in a single point at the Fermi level without SOC (Fig. 3(a) and 3(b)). These meeting points of valence and conduction bands are Dirac points equivalent to those of graphene. Around the meeting point, both the valence and conduction bands (referred to as Dirac bands) are linear and can be characterized by Dirac cones. The charge carriers (electrons and holes) in these bands will behave as massless Dirac fermions, similar to the cases of the well-known Dirac-fermion materials such as graphene44, silicene45, germanene45 and silicon germanide46. We also evaluated the Fermi velocity (νf) of the δ-graphyne by fitting these two bands at k = K + q to the expression of  . The Fermi velocities of electrons and holes are identical in our calculations, which are 6.96 × 105 m/s. This value is about 56% of value of graphene, 8.22 × 105 m/s from the present calculations. Noting that that the Dirac cones of the δ-graphyne differ significantly from those of the 6,6,12-graphyne proposed in the Ref. 28 in both positions and shapes. Due to the rectangular symmetry, the 6,6,12-graphyne has four Dirac cones which are distorted and direction-dependent in its BZ28. Therefore, δ-graphyne can be regarded as the most stable counterpart of graphene in electronic structures among the graphynes.
. The Fermi velocities of electrons and holes are identical in our calculations, which are 6.96 × 105 m/s. This value is about 56% of value of graphene, 8.22 × 105 m/s from the present calculations. Noting that that the Dirac cones of the δ-graphyne differ significantly from those of the 6,6,12-graphyne proposed in the Ref. 28 in both positions and shapes. Due to the rectangular symmetry, the 6,6,12-graphyne has four Dirac cones which are distorted and direction-dependent in its BZ28. Therefore, δ-graphyne can be regarded as the most stable counterpart of graphene in electronic structures among the graphynes.
(a) Band lines (without SOC) of δ-graphyne in proximity of the Fermi level (set to zero) along the high symmetric points in the BZ. The data obtained from DFT calculations (solid lines) and TB model (red dotted lines) are presented separately for propose of comparison. (b) Two-dimensional profile of the two Dirac bands in reciprocal space. The Dirac cones at the K and K/ points are obvious. (c) Brillouin zone with high symmetric points labeled.
Charge density distribution of the two Dirac bands in proximity of the Fermi level and the electron density of states (PDOS) projected onto the s and p (px, py and pz) orbitals of the atoms labeled as C1, C2 and C3 are then employed to reveal the origins of the Dirac cones. From Fig. 4 (a) and 4(b), it is obvious that electronic states in proximity of the Fermi level arise mainly from the pz orbitals of carbon atoms which are perpendicular to the basal plane of the δ-graphyne. The electronic states contributed by the px, py and s states locate in the region ~2 eV away from the Fermi level. The interactions between the pz orbitals lead to the formation of π-conjugated framework. These features allow us to model the electronic structures in proximity of the Fermi level using a simple tight-binding (TB) Hamiltonian of the π-electrons:

where  and ci represent the creation and annihilation operators of an electron at the ith atom, respectively. The parameter tij is the hopping energy of an electron between the i-th and j-th atoms. For simplification, we only considered the hopping between the nearest-neighboring (NN) atoms. Corresponding to the three types of carbon atoms (C1, C2 and C3) in the δ-graphyne framework (Fig. 1(a)), there are four types of NN hopping energies which are tC1-C1, tC1-C2, tC2-C2 and tC2-C3, respectively. Noting that the lengths of the bonds (C1-C1, C1-C2 and C2-C3) are very close with the difference less than 0.04 Å, whereas that of the C2-C2 bond is much shorter, we therefore set tC1-C1, tC1-C2 and tC2-C3 to be identical to the value in graphene, 2.7 eV and tC2-C2 to 3.0 eV. Through diagonalizing a 20 × 20 matrix in the reciprocal space, the electronic band structures can be obtained, as indicated by the red dash lines in Fig. 3(a). Obviously, this simple TB Hamiltonian can reproduce well the band lines of the δ-graphyne in proximity of the Fermi level given by DFT calculations, especially the appearance of the Dirac cones as well as the profiles of the two Dirac bands. Further studies show that the appearance of the Dirac cones is independent of the NN hopping energies, suggesting that it is the intrinsic feature of such π-conjugated δ-graphyne framework.
and ci represent the creation and annihilation operators of an electron at the ith atom, respectively. The parameter tij is the hopping energy of an electron between the i-th and j-th atoms. For simplification, we only considered the hopping between the nearest-neighboring (NN) atoms. Corresponding to the three types of carbon atoms (C1, C2 and C3) in the δ-graphyne framework (Fig. 1(a)), there are four types of NN hopping energies which are tC1-C1, tC1-C2, tC2-C2 and tC2-C3, respectively. Noting that the lengths of the bonds (C1-C1, C1-C2 and C2-C3) are very close with the difference less than 0.04 Å, whereas that of the C2-C2 bond is much shorter, we therefore set tC1-C1, tC1-C2 and tC2-C3 to be identical to the value in graphene, 2.7 eV and tC2-C2 to 3.0 eV. Through diagonalizing a 20 × 20 matrix in the reciprocal space, the electronic band structures can be obtained, as indicated by the red dash lines in Fig. 3(a). Obviously, this simple TB Hamiltonian can reproduce well the band lines of the δ-graphyne in proximity of the Fermi level given by DFT calculations, especially the appearance of the Dirac cones as well as the profiles of the two Dirac bands. Further studies show that the appearance of the Dirac cones is independent of the NN hopping energies, suggesting that it is the intrinsic feature of such π-conjugated δ-graphyne framework.
Now that such δ-graphyne can be regarded as an ideal counterpart of graphene with superior stability among the graphynes, the SOC in δ-graphyne becomes interesting. We therefore switch on SOC in our DFT calculations. As a benchmark, we first calculated the SOC gap in graphene and fond that it is only 0.008 meV, close to the value of previous works11. Using the same method, we calculated the band structures of δ-graphyne in the vicinity of the Fermi level. The band gap opened by SOC for the π orbital at the Dirac point is about 0.59 meV, as shown in Fig. 5(a), which corresponds to 7 K. This value is much larger than that of graphene, suggesting that the effective SOC in δ-graphyne is stronger than that in graphene. Consequently, QSHE can be observed in an experimentally accessible low temperature regime (<7 K) in δ-graphyne. We also evaluated the SOC gap of α-graphyne at the Dirac points using the same method and found that it is only 0.014 meV which is much smaller than that in δ-graphyne. This implies that the presence of acetylenic bonds is not always associated with drastic increase of SOC strength. For 6,6,12-graphyne, although the SOC gap opened in each Dirac cone is in the order of ~0.5 meV, there is no gap throughout the BZ due to the self-doping effect.
(a) Enlarged view of the two Dirac bands (with SOC) nearest to the Fermi level in vicinity of the K point. The profiles of the Dirac bands with and without SOC are very similar. Only the enlarged view in close vicinity of the K point is presented. (b) Brillouin zone with the values of δi associated with the time-reversal invariant momenta. b1 and b2 are the primitive reciprocal lattice vectors.
In the presence of SOC, the TB Hamiltonian for the δ-graphyne is written as5:

In addition to the nearest-neighbor hopping term (the first term), the spin-orbital interaction with spin-dependent second-nearest-neighbor hopping is involved (the second term). λSO is spin-orbital coupling strength and S is the spin. The unit vector  is defined as:
is defined as:

where  and
and  are bond vectors along the two bonds that the electron traverses when going from atom j to i. According to this definition,
are bond vectors along the two bonds that the electron traverses when going from atom j to i. According to this definition,  . Based on the above Hamiltonian with λSO = 0.4 meV, the two Dirac bands are well reproduced as shown in Fig. 5(a).
. Based on the above Hamiltonian with λSO = 0.4 meV, the two Dirac bands are well reproduced as shown in Fig. 5(a).
The low energy effective Harmiltonian with SOC in graphene in the vicinity of Dirac point K can be described by

where νF is the Fermi velocity of π electrons near the Dirac points and σz is Pauli matrix. The effective SOC ξ for graphene has the explicit from  , with Δε being the energy difference between the 2s and 2p orbitals and
, with Δε being the energy difference between the 2s and 2p orbitals and  half of the intrinsic spin-orbital strength, respectively13. The parameter Vspσ corresponds to the σ bond formed by the 2s and 2p orbitals. This effective Harmiltonian leads to a spectrum
half of the intrinsic spin-orbital strength, respectively13. The parameter Vspσ corresponds to the σ bond formed by the 2s and 2p orbitals. This effective Harmiltonian leads to a spectrum  . The energy gap at the Dirac point is 2ξ. For graphene, ξ was estimated to be of order of 10−3 meV13. Supposing that this effective Harmiltonian still holds for δ-graphyne, because they have similar electronic bands structures in the vicinity of Dirac point K, ξ is estimated to be about 0.3 meV from our first-principles calculations, almost three orders of graphene. The physical reasons behind the vastly enhanced SOC gap size compared to graphene are related to the unique framework of δ-graphyne. Basically, the SOC is a relativistic effect described by a Hamiltonian with the form
. The energy gap at the Dirac point is 2ξ. For graphene, ξ was estimated to be of order of 10−3 meV13. Supposing that this effective Harmiltonian still holds for δ-graphyne, because they have similar electronic bands structures in the vicinity of Dirac point K, ξ is estimated to be about 0.3 meV from our first-principles calculations, almost three orders of graphene. The physical reasons behind the vastly enhanced SOC gap size compared to graphene are related to the unique framework of δ-graphyne. Basically, the SOC is a relativistic effect described by a Hamiltonian with the form  ,
,  is the Pauli matrix. The SOC strength is proportional to the grad of electric potential
is the Pauli matrix. The SOC strength is proportional to the grad of electric potential  . The presence of acetylenic bonds in the δ-graphyne framework enhances the local inhomogenity of electron distribution and thus the grad of electronic potential compared to the case of graphene. This is also the reason why the SOC gap sizes of other 2D carbon allotropes (α- and 6,6,12-graphynes) are larger than that of graphene. Obviously, the enhancement of electric potential grad depends on the distribution pattern of the acetylenic bonds, because α-graphyne possesses the smallest SOC gap size among the three graphynes.
. The presence of acetylenic bonds in the δ-graphyne framework enhances the local inhomogenity of electron distribution and thus the grad of electronic potential compared to the case of graphene. This is also the reason why the SOC gap sizes of other 2D carbon allotropes (α- and 6,6,12-graphynes) are larger than that of graphene. Obviously, the enhancement of electric potential grad depends on the distribution pattern of the acetylenic bonds, because α-graphyne possesses the smallest SOC gap size among the three graphynes.
The topologically nontrivial electronic structures of δ-graphyne can be confirmed by calculating the Z2 topological invariant. The work of Fu and Kane showed that the inversion symmetry can simplify the calculations of the Z2 invariants5. In their strategy, the Z2 invariant v is defined by

with

for 2N occupied bands. ζ2m(Γi) = ±1 is the parity eigenvalue of the 2m-th occupied energy band at the time-reversal invariant momentum Γi. The two states of a Kramers doublet have the same parity, ζ2m = ζ2m−1. It means that with inversion symmetry, the Z2 topological invariants can be deduced from the knowledge of the parity of the four time-reversal and parity invariant points at BZ. This provides a simple method for determining the topological phase of any inversion symmetric insulator, without having to know about the global properties of the energy bands. For the honeycomb δ-graphyne lattice, the four time-reversal invariant momenta occur at Γi = (n1 n2) = (n1b1 + n2b2)/2 with n1, n2 = 0, 1 and b1, b2 are primitive reciprocal lattice vectors, which correspond to the Γ and three M points in BZ, as shown in Fig. 5(b). Using this strategy, we calculated the Z2 topological invariant based on the above-mentioned TB Hamiltonian and found that v = 1. This confirms that δ-graphyne is a topological insulator in the quantum spin-Hall phase. Noting that the Fermi level is right within the SOC band gap, doping is therefore unnecessary in realizing QSHE in δ-graphyne.
Discussion
We should stress that although δ-graphyne is kinetically stable and energetically more favorable than the already-synthesized graphdiyne, its synthesis remains challenging for chemists. Neither γ-graphyne nor 6,6,12-graphyne has been realized in experiments, even though both of them are lower in energy than δ-graphyne. However, the recent progresses on the growth of graphene on metal surfaces by chemical vapor deposition or organics precursor molecules may also be helpful for reaching this goal. Anyway, our work suggests that the observation of TIs may be within rich in 2D carbon allotropes beyond graphene. The acetylenic bonds associated with sp-hybridized carbon atoms in these allotropes introduce a rich variation in electronic properties superior to graphene. Interestingly, the unique framework with Dirac-cone characterized electronic structures is also useful for the design of other 2D materials, because the appearance of the Dirac cones is independent of the NN hopping energies as revealed by TB model. For example, one can replace the C3 atom of δ-graphyne with silicon or other atoms to get novel 2D Dirac materials.
In conclusion, using first-principles calculations combined with a tight-binding model, we propose a two-dimensional carbon topological insulator (δ-graphyne) beyond graphene with superior energetic stability and remarkable spin-orbital interactions. The electronic band structures in proximity of the Fermi level of the π-conjugated framework resembles well those of graphene characterized by the appearance of Dirac cones at the K and K/ points, but the spin-orbital interaction is more remarkable. The band gap opened up at the Dirac points due to SOC is about 0.59 meV and can host the QSHE in an experimentally accessible low temperature regime (<7 K). The topologically nontrivial electronic structures of δ-graphyne in the quantum spin-Hall phase is identified by a Z2 topological invariant of v = 1. This provides a viable approach for searching new TIs in 2D carbon allotropes.
Methods
We performed first-principles calculations within DFT using the Vienna ab initio simulation package (VASP)47,48. The electron-electron interactions are treated within a generalized gradient approximation (GGA) in the form of Perdew-Burke-Ernzerhof (PBE) for the exchange-correlation functional49. Projector-augmented-wave (PAW) potentials are adopted to describe the electron-ion interaction50. The electron wavefunctions are expanded using the plane-waves with the energy cutoff of 800 eV. Self-consistent solution of the Kohn-Sham equation is carried out with the convergence of 10−8. The supercells are repeated periodically on the x-y plane while a vacuum region of about 15 Å is applied along the z-direction to avoid mirror interaction between neighboring images. A symmetry reduced (9 × 9 × 1) Monkhorst-Pack sampling is used for the Brillouin zone (BZ) integration. The convergence of gap size with respect to the number of k points and cutoff energy is better than 1 × 10−3 meV. Structural optimizations are carried out using a conjugated gradient (CG) method until the remaining force on each atom is lower than 0.001 eV/Å.
References
Kane, C. L. & Mele, E. J. Z2 Topological order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 226802 (2005).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Fu, L. & Kane, C. L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 100, 096407 (2008).
Fu, F. & Kane, C. L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction. Phys. Rev. B 79, 161408 (2009).
Seradjeh, B., Moore, J. E. & Fanz, M. Exciton Condensation and Charge Fractionalizationin a Topological Insulator Film. Phys. Rev. Lett. 103, 066402 (2009).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamicsin crystalline Insulators. Phys. Rev. Lett. 102, 146805 (2009).
Meng, Q., Shivamoggi, V., Hughes, T. L., Gilbert, M. J. & Vishveshwara, S. Fractional spin Josephson effect and electrically controlled magnetizationin quantum spin Hall edges. Phys. Rev. B 86, 165110 (2012).
Nagaosa, N. A new state of quantum matter. Science 318, 758–759 (2007).
Yao, Y. G., Ye, F., Qi, X.-L., Zhang, S.-C. & Fang, Z. Spin-orbit gap of graphene: First-principles calculations. Phys. Rev. B 75, 041401 (2007).
Min, H. et al. Intrinsic and Rashba spin-orbit interactions in graphene sheets. Phys Rev B 74, 165310 (2006).
Boettger, J. C. & Trickey, S. B. Erratum: First-principles calculation of the spin-orbital splitting in graphene. Phys. Rev. B 75, 121402 (2007).
Gmitra, M., Konschuh, S., Ertler, C., Ambrosch-Draxl, C. & Fabian, J. Band-structure topologies of graphene: Spin-orbit coupling effects from first principles. Phys. Rev. B 85, 235431 (2009).
Weeks, C., Hu, J., Alicea, J., Franz, M. & Wu, R. Q. Engineering a Robust Quantum Spin Hall State in Graphene via Adatom Deposition. Phys. Rev. X 1, 021001 (2011).
Ding, J., Qiao, Z. H., Feng, W. X., Yao, Y. G. & Niu, Q. Engineering quantum anomalous/valley Hall states in graphene via metal-atom adsorption: An ab-initio study. Phys. Rev. B 84, 195444 (2011).
Zhang, H., Lazo, C., Blügel, S., Heinze, S. & Mokrousov, Y. Electrically tunable quantum anomalous Hall effect in graphene decorated by 5d transition-metal adatoms. Phys. Rev. Lett. 108, 056802 (2012).
Jiang, H., Qiao, Z. H., Liu, H. W., Shi, J. R. & Niu, Q. Stabilizing topological phases in graphene via random adsorption. Phys. Rev. Lett. 109, 116803 (2012).
Hu, J., Alicea, J., Wu, R. Q. & Franz, M. Giant topological insulator gap in graphene with 5d adatoms. Phys. Rev. Lett. 109, 266801 (2012).
Wang, Z. F., Ninghai Su, N. & Liu, F. Prediction of a Two-Dimensional Organic Topological Insulator. Nano Lett. 13, 2842–2845 (2013).
Wang, Z. F., Liu, Z. & Liu, F. Organic topological insulators in organometallic lattices. Nature Commun. 4, 1471–1475 (2013).
Liu, Z., Wang, Z. F. & Liu, F. Flat Chern Band in a Two-Dimensional Organometallic Framework. Phys. Rev. Lett. 110, 106804 (2013).
Wang, Z. F., Liu, Z. & Liu, F. Quantum anomalous Hall effect in 2D organic topological insulator. Phys. Rev. Lett. 110, 196801 (2013).
Zhao, M. W., Wang, A. Z. & Zhang, X. M. Half-metallicity of a kagome spin lattice: the case of a manganese bis-dithiolene monolayer. Nanoscale 5, 10404–10408 (2013).
Baughman, R. H. & Eckhardt, H. Structure-property predictions for new planar forms of carbon: layered phases containing sp2 and sp atoms. J. Chem. Phys. 87, 6687–6699 (1987).
Coluci, V. R., Braga, S. F., Legoas, S. B., Galvão, D. S. & Baughman, R. H. Families of carbon nanotubes: graphyne-basednanotubes. Phys. Rev. B 68, 035430 (2003).
Hirsch, A. The era of carbon allotropes. Nat. Mater. 9, 868–871 (2010).
Malko, D., Neiss, C., Ciñes, F. & Görling, A. Competition for graphene: Graphynes with direction-dependent Dirac cones. Phys. Rev. Lett. 108, 086804 (2012).
Bunz, U. H. F., Rubin, Y. & Tobe, Y. Polyethynylated cyclic π-systems: scaffoldings for novel two and three-dimensional carbon networks. Chem. Soc. Rev. 28, 107–119 (1999).
Kehoe, J. M. et al. Carbon networks based on dehydrobenzoannulenes. 3. Synthesis of Graphyne Substructures. Org. Lett. 2, 969–72 (2000).
Marsden, J. A., Palmer, G. J. & Haley, M. H. Synthetic Strategies for Dehydrobenzo[n]annulenes. Eur. J. Org. Chem. 2003, 2355–2369 (2003).
Gholami, M. et al. Synthesis and characterization of a new generation of expanded radialenes, bis-radialenes and radiaannulenes. Angew. Chem. Int. Ed. 46, 9081–9085 (2007).
Yoshimura, T. et al. Synthesis and Properties of Trefoil-Shaped Tris (hexadehydrotribenzo[12]annulene) and Tris(tetradehydrotribenzo[12] annulene). Org. Lett. 8, 2933–2936 (2006).
Diederich, F. & Kivala, M. All-Carbon Scaffolds by Rational Design. Adv. Mater. 22, 803–810 (2010).
Li, G. X. et al. Architecture of graphdiyne nanoscale films. Chem. Commun. 46, 3256–3258 (2010).
Narita, N., Nagai, S., Suzuki, S. & Nakao, K. Optimized geometries and electronic structures of graphyne and its family. Phys. Rev. B 58, 11009 (1998).
Zhou, J. et al. Electronic structures and bonding of graphyne sheet and its BN analog. J. Chem. Phys. 134, 174701–174705 (2011).
Konstantinov, E., Dantas, S. O. & Barone, P. M. V. B. Electronic and elastic properties of two-dimensional carbon planes. Phys. Rev. B 74, 035417 (2006).
Long, M., Tang, L., Wang, D., Li, Y. & Shuai, Z. Electronic structure and carrier mobility in graphdiyne sheet and nanoribbons: Theoretical predictions. ACS Nano 5, 2593–2600 (2011).
Pan, L. D., Zhang, L. Z., Song, B. Q., Du, S. X. & Gao, H.-J. Graphyne- and graphdiyne-based nanoribbons: Density functional theory calculations of electronic structures. Appl. Phys. Lett. 98, 173102–173104 (2011).
Enyashin, A. N. & Ivanovskii, A. L. Graphene allotropes. Phys. Status Solidi B 248, 1879–1883 (2011).
Zhang, H. Y. et al. High mobility and high storage capacity of lithium in sp–sp2 hybridized carbon network: The case of graphyne. J. Phys. Chem. C 115, 8845–8850 (2011).
Luo, G. et al. Quasiparticle energies and excitonic effects of the two-dimensional carbon allotrope graphdiyne: Theory and experiment. Phys. Rev. B 84,075439 (2011).
Gelm, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Liu, C.-C., Feng, W. X. & Yao, Y. G. Quantum Spin Hall Effect in silicene and two-dimensional germanium. Phys. Rev. Lett. 107, 076802 (2011).
Zhou, H. C. et al. First-principles prediction of a new Dirac-fermion material: silicon germanide monolayer. J. Phys. Condens. Mater. 25, 395501–295505 (2013).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Acknowledgements
This work is supported by the National Basic Research Program of China (No. 2012CB932302), the National Natural Science Foundation of China (No.91221101), the 111 project (no. B13209) and National Super Computing Centre in Jinan.
Author information
Authors and Affiliations
Contributions
M.Z. conceived the study and performed most of the calculations, analyzed the data, drafted and revised the manuscript. W.D. calculated the phonon spectrum. A.W. contributed to the calculations and analysis of PDOS. All authors read and approved the final manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Zhao, M., Dong, W. & Wang, A. Two-dimensional carbon topological insulators superior to graphene. Sci Rep 3, 3532 (2013). https://doi.org/10.1038/srep03532
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03532
This article is cited by
-
Colossal figure of merit and compelling HER catalytic activity of holey graphyne
Scientific Reports (2023)
-
Exploring strong and weak topological states on isostructural substitutions in TlBiSe\(_2\)
Scientific Reports (2022)
-
A first principles investigation on the structural, mechanical, electronic, and catalytic properties of biphenylene
Scientific Reports (2021)
-
Synthesis of radiaannulene oligomers to model the elusive carbon allotrope 6,6,12-graphyne
Nature Communications (2019)
-
Design of 2D massless Dirac fermion systems and quantum spin Hall insulators based on sp–sp2 carbon sheets
npj Computational Materials (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.