Introduction

The recent work of Murdin et al.1 impressively demonstrates that an impurity atom in a semiconductor host acts as a hydrogen atom in a white dwarf star, yet in a laboratory magnetic field about one thousand times less than the stellar field. In free hydrogen, the space between the proton and the electron is a vacuum. In the laboratory analogue, the introduced P+ atom and the donated e− are immersed in a crystal of Si. The effective mass, m*, of the electron is decreased and the relative permittivity, , of the medium is increased with respect to the vacuum values of me and 1. Both changes work to increase the orbital radius, , from the Bohr radius a0, to decrease the binding energy, , from the Rydberg R and to reduce the characteristic magnetic field, , from the value for the hydrogen atom (where e, κ and are the electron charge, Coulomb constant and reduced Planck constant, respectively). Importantly, the crystal matrix introduces another factor—a reduction in symmetry. The previous work was limited to magnetic fields along the 〈100〉 crystallographic direction. Varying the crystal direction relative to the magnetic field gives an additional control. Another magnetic field orientation, B||〈111〉, is noteworthy. This is the unique orientation for which all six conduction-band valleys make the same angle with the magnetic field. Consequently, the six conduction-band valleys are all equivalent. It follows that the energy levels and the allowed transitions, are simpler than for the 〈100〉 orientation. Here we present data for B||〈111〉 in Si:P to an equally high field (30 T), supported by new calculations, simultaneously comprehensively confirming and extending the previous work and allowing a simpler comparison with the hydrogen atom, as the fewer transitions involved are easier to identify.

Results

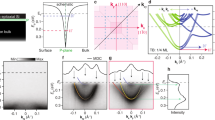
As Murdin et al.1 point out, the hydrogenic Lyman spectra are simple both at low field, where the magnetic field can be treated as a perturbation and at high field, where the Coulomb field can be treated as a perturbation. The most interesting, complex and challenging region is the intermediate field and we will focus our attention on this. Figure 1 shows the Lyman spectrum for Si:P that we have calculated (full lines) and measured (circled dots). We will now compare these new results both to the previous calculations of the hydrogen spectrum (Fig. 3 of ref. 1) and to the previous calculations and experiments for the Si:P spectrum (Fig. 2 of ref. 1). We note our results are in good agreement with those of Mu et al.2 as far as that work extends, to 10 T.

Figure 1
figure 1

Calculated (lines) and observed (circled dots) frequencies of Lyman transitions for Si:P as a function of magnetic field B for B||〈111〉.

Full size image

With respect to the hydrogen spectrum, Fig. 3 of ref. 1, we note that the exact solution has been given previously by Kravchenko et al.3 with numerical values listed for the states 1s, 2s, 2p0, 2p−, 3p0, 3p−, 3d− and 3d2−. We have calculated the states of hydrogen using a finite-difference method4 and now using a Rayleigh-Ritz method and in each case obtain excellent agreement with the values given in ref. 3. Turning now to the Si:P spectrum, the exact method of solution cannot be applied due to the complication of crystalline anisotropy. The finite-difference method is still applicable, but involves large matrices4. Instead, we employ a variational method5, which uses much smaller matrices and so is much more efficient. Since our previous work5 we have improved the minimisation. Details are given in the Methods section below. The Lanczos procedure of ref. 1 represents another calculational approach.

We divide our discussion into two parts, separated by the prominent 2p+ transition, which runs diagonally from the bottom middle to the top right corner of Fig. 1. We first consider lower-energy transitions, that is, ones lying to the left of the 2p+ transition in Fig. 1. In the hydrogen spectrum (Fig. 3 of ref. 1), along with 2p+, the transitions originating from the zero-field n = 2 transition (at ) are 2p− and 2p0. (The 2s state also originates here, but transitions are forbidden from the ground state 1s to the 2s state, so it is not displayed.) The other transitions in this energy regime are the pairs 3p−/3p0, 4p−/4p0 and 5p−/5p0, all shown (but not labelled) on Fig. 3 of ref. 1. Compare this with the case of Si:P, B||〈100〉, Fig. 2 of ref. 1. A conspicuous difference is that the crystal symmetry lifts the degeneracy of the n = 2 states; the state labelled 2pox has a different energy to the 2p± states, even in the absence of magnetic field. As well, the region between the 2p− and 3p− transitions no longer has a lone transition (2p0), but four transitions now appear. The high-energy region at the highest magnetic fields is even more cluttered, with some ten additional unpolarised transitions in addition to the clear 3p−, 4p− and 5p−. Finally, compare with the case of Si:P, B||〈111〉 shown in Fig. 1. The split-off 2p0 state is evident, well separated from the others, as for B||〈100〉. However, in contrast to B||〈100〉, the region between the 2p− and 3p− is much less cluttered, containing only the 3p0 state. Moreover, in the high-energy, high-field region, there are far fewer transitions expected and observed and there is an excellent agreement between experiment and calculation.

Turning now to the 2p+ transition itself, in contrast to B||〈100〉, the B||〈111〉 orientation yields repeated examples of anti-crossing. The first three anti-crossings are clear in the experimental data. The theoretical absorption intensities calculated as function of magnetic field reveal seven anti-crossings within the field range 0–30 T.

Finally, to better deal with transitions of higher energies than the 2p+ transition, we will focus on the low-field region 0–6 T (Fig. 2, Fig. 3). Both the positions and the intensities of the observed and calculated transitions are shown. In comparison to Fig. 5 of ref. 1, at the lowest energies and fields we distinctly observe the 4p0 transition. The data for that transition and the repulsion of the adjacent 3p− transition, are very distinct and in excellent agreement with the calculations. In the same way, the data for the 3p− transition follows the calculation very precisely, with a second anti-crossing evident at about 5 T. The simpler crystallographic orientation means the whole region is less cluttered than for B||〈100〉; in particular, the most intense transitions of Fig. 5 of ref. 1, occurring between the 3p± and 4p± zero-field energies, do not appear at all for B||〈111〉, leaving a striking example of a crossing at around 2 T in the middle of this energy range. Further such detailed observations may be made; however, this becomes progressively more difficult at higher energies due to the diminishing intensities and increasing number of the transitions.

Figure 2
figure 2

Calculated and observed frequencies and strengths of Lyman transitions for Si:P as a function of magnetic field B for B||〈111〉 in the region of high energy and low magnetic field.

Circles represent the experimental data; the radii are proportional to the area of the absorption peaks. Lines represent the theoretical data; the widths of the lines are proportional to the square root of the calculated absorption strengths.

Full size image
Figure 3
figure 3

Experimental spectra of Si:P at magnetic fields of B = 0, 1 and 2 T with B||〈111〉.

The absorption coefficient has been calculated in the usual way. For clarity, the spectra for 1 and 2 T have been offset on the vertical axis by 10 and 20 cm−1, respectively. As highlighted, the lower branch of the transition labelled 3p± interacts with the transition labelled 4p0 at around 1 T and the upper branch of transition labelled 3p± interacts with the transition labelled 4f0 (not evident at 0 T) at around 2 T.

Full size image

To conclude, the general problem of the semiconductor analogue of free hydrogen in a magnetic field involves three symmetries: the crystal tetrahedral symmetry interacting with the magnetic field cylindrical symmetry and the electric (Coulombic) spherical symmetry. We have made measurements and calculations to magnetic fields at which the cyclotron energy approaches the binding energy with the field along the simplest crystal direction. Clear-cut agreement is found between the data and model, increasing confidence in the extension of such laboratory analogues to astrophysical phenomena.

Methods

Experimental methods

The sample used was a single crystal of silicon doped by neutron transmutation to a phosphorous concentration of ~1 × 1014 cm−3. The residual concentration of other donors and acceptors was estimated to be below 1012 cm−3; no transitions other than from Si:P were observed in the spectra. The sample was wedged to suppress interference fringes. Data to 30 T with the sample at 4.2 K were collected using a Bruker 113v Fourier spectrometer operating at unapodised resolution of 1 cm−1 (0.03 THz, 0.12 meV). Data to 6 T with the sample at 10 K were collected using a modified Polytec Fourier spectrometer operating at unapodised resolution of 0.4 cm−1 (0.01 THz, 0.05 meV). In both cases, a liquid-helium-cooled Si-composite bolometer was used as the detector.

Theoretical methods

The effective-mass equation for the donor impurity in silicon is solved for a single valley of the conduction band and the symmetric gauge is chosen for the magnetic field. With the field along the [111] direction, the six valleys are equivalent and we disregard both the coupling between them and the central-cell correction. The latter is expected to be relevant for the ground 1s state only. Therefore, the dependence of the ground energy level on the magnetic field strength is corrected by fitting the experimental data for 1s → 2p0 transition energies. As a result, the 1s level is shifted by ΔE = −115.45 − 0.00225 B2, with B given in Tesla. For the calculation of the dipole transition matrix elements, however, we retain the uncorrected 1s wavefunction.

Because of the inversion symmetry, the donor wavefunctions are symmetric or antisymmetric. The ground state belongs to the first class, while the excited states of the dipole-allowed transitions are of the second class. The donor states are calculated by the Rayleigh-Ritz method6. Each state is given by a linear combination of elongated, scaled and orthonormal hydrogenic orbitals of the following form2,5:

where n, l and m are the atomic quantum numbers. The elongation is given by the variational parameter β, which is expected to take into account the anisotropy induced by the effective mass and the magnetic field, while the scaling variational parameter ξl,m is intended to adjust the size of the basis function for the combined effect of the Coulomb and magnetic fields. The symmetry of the basis functions is chosen to agree with the symmetry of the donor state. The Hamiltonian matrix elements are calculated analytically2. Hence, for each symmetry and for given values of the elongation and scaling variational parameters, a simple diagonalisation technique produces a set of estimates for the donor energies and the corresponding coefficients of the linear combinations. Moreover, each donor state may be improved separately, by minimising the corresponding energy as a function of the elongation and scaling variational parameters.

For each symmetry, the calculations have been performed by including the states with n ≤ 6. This leads to a set of 47 (44) basis functions for the symmetric (antisymmetric) donor states and the energy minimisation is performed over the elongation parameter β and the 21 (15) scaling variational parameters. The relatively large number of variational parameters gives some flexibility to the trial wavefunctions. Accordingly, the energy of each level may present multiple local minima. Since iterative minimisation procedures are used, several choices of the starting points are made in order to reach the lowest local minimum. The simplest of such choices is the set of variational parameters that minimises the trace of the Hamiltonian matrix5,6.

After the energy levels and the parameters of the variational trial functions have been obtained as a function of the magnetic-field strength, the 1s→(antisymmetric state) transition energies and the corresponding absorption strengths are determined. For unpolarised radiation, the latter is directly proportional to the square of the matrix element of the electron position times the transition energy7.