Abstract
By using a half soap bubble heated from below, we obtain large isolated single vortices whose properties as well as their intensity are measured under different conditions. By studying the effects of rotation of the bubble on the vortex properties, we found that rotation favors vortices near the pole. Rotation also inhibits long life time vortices. The velocity and vorticity profiles of the vortices obtained are well described by a Gaussian vortex. Besides, the intensity of these vortices can be followed over long time spans revealing periods of intensification accompanied by trochoidal motion of the vortex center, features which are reminiscent of the behavior of tropical cyclones. An analysis of this intensification period suggests a simple relation valid for both the vortices observed here and for tropical cyclones.
Similar content being viewed by others
Introduction
Vortices are prominent features of fluid flows and span length scales ranging from an insect's length1 to planetary sizes2. Understanding the displacement of vortices, their structure and their long time dynamics is crucial for different aspects be they at the level of small engines, turbulent flows, or planetary atmospheres3. Vortices may be found in turbulent flows, where they appear at all scales, in the wake of a bluff body, where they come in pairs, or in atmospheric flows whether on earth or on other planets3,4. In the latter case, these single vortices may be giant and very long lived such as the famous great red spot on Jupiter2 or the great dark spot in Neptune5. Or they may be short lived and capable of traveling long distances such as tropical cyclones (TC) on earth6,7. The exact structure of planetary vortices and notably that of the great red spot is still debated but some of their features are known. The two great spots are elliptical for example5,8,9 and tropical cyclones can be reasonably modeled with a modified version of an ideal vortex known as the Rankine vortex10 or even more refined models introduced recently11. Nonetheless and when it comes to predicting their trajectories (as for TCs on earth), the evolution of their intensity, or their lifetime, vortices still pose a number of problems mainly because the interactions with the environment are complex7,12,13. For example, the intensity of tropical cyclones and its temporal evolution is an issue which has been tackled over the past few decades with some success as thermodynamical models as well as simple coupled ocean atmosphere models seem to capture some of the essential features12,14. Its prediction remains an arduous task as there is need to consider several factors such as the interaction with the sea and the environment, the structure of the TC itself, as well as the role of rotation on the dynamics of such vortices13,15. It is therefore highly desirable to devise experimental systems to study the generic properties as well as the effects of such single vortices16,17,18,19,20,21. It goes without saying that such experimental systems may bring insight into the vastly complex problem of Tropical cyclone intensity or the stability of giant planetary vortices, however, care has to be taken in using results from such systems considering the large differences in the mechanisms at play between the model systems and their natural counterparts.
Here we use a half bubble heated from below on which large isolated vortices are observed. We first characterize the general properties of these vortices (their displacement and location on the bubble surface, their life time) with and without rotation of the bubble to gauge the effects of rotation on such a situation. Second, we characterize these vortices by measuring their velocity and vorticity profiles. In a third stage and based on the preceding velocity measurements, we analyze the long time behavior of the rotation rate of these vortices. The measurements show that the system at hand exhibits a number of intriguing features such as intensification of vortices and trochoidal motion which are common in natural vortices such as tropical cyclones.
For the sake of making such qualitative observations more quantitative, the measurements of intensification periods are then compared to the long time variation of the intensity of tropical cyclones. The rationale behind this comparison is very simple. Since the vortices here and Tropical cyclones are large vortices with dimensions much larger than the thickness of the bubble membrane or of the atmosphere respectively, both may be considered as two dimensional objects. This is a huge simplification of the tropical cyclone structure so its limitations will be kept in mind. The results show that parallels may be drawn.
Results
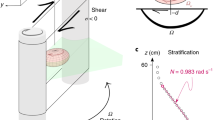
The system used here is a half bubble heated from below18,19,22 in a specially designed cell capable of rotating the bubble at different rates (see methods and figure 1). Once formed, the bubble is subject to strong convection due to the heating at the base of the bubble22. Care was taken so that the air within the bubble does not generate additional convection so a priori the convection on the bubble surface is due solely to the heating at the base of the bubble. Images of the bubble with well defined thermal plumes are shown in figure 1b and c. After a short period, a large vortex may emerge. The emergence of vortices occurs both for bubbles not subject to rotation as well as under the rotation of the bubble. The formation of such vortices usually occurs when a large plume, which is the result of the merging of a few smaller ones, rises to near the top of the bubble and forms a swirl as shown in figure 1d. While this is one possible way to form such vortices, our study did not allow us to discover all the possible ways leading to the formation of such vortices. Once formed, the large vortices are followed using video imaging. A large vortex of this sort is visible in figure 1e. Note that the vortex has a well defined center or ‘eye’ and develops as a spiral looking structure of dimensions between 1 and 2 cm. By using numerical simulations of two dimensional thermal convection on a sphere23, we obtain a roughly similar phenomenology as the experimental system although the effects of rotation have not been examined in the numerical simulations. Figure 1f and 1g show a snapshot of the thermal convection obtained as well as the presence of a large single vortex. The nice agreement between the numerical observations and the observations carried out in the soap bubble comfort our initial assumption that the dynamics on the bubble surface is quasi two dimensional.
The bubble: (a) Set up: a brass disk (1) with a circular groove (3) can be rotated using a continuous motor (6) connected to it by a shaft (5). This disk is heated by the proximity of a hollow annulus (2) connected to a water circulation bath. The bubble is blown using the soap solution in the groove (3). The inner side of the brass disk is covered by a Teflon coating (2 mm thick) to minimize the heating of the air inside the bubble. The temperature at the equator of the bubble is set by the temperature of the water bath. (b) and (c) Images showing the detachment of thermal plumes from near the equator and rising towards the pole taken using an infrared camera (the temperature scale is in deg °C) (b) and a CCD color camera (c). (d) Image of the full bubble with a vortex being formed by a large thermal plume. (e) A zoom on the vortex, the colors are interference colors of white light being reflected by the thin water layer constituting the bubble. (f) Numerical simulation of thermal convection on the surface of a sphere of radius 1, the colors indicate the vorticity field. g) a zoom on the single vortex in image (f). The color code indicates the value of the vorticity and the grid used is 2048 × 2048.
Let us first focus on some general properties of these vortices such as their location on the bubble surface and their lifetime. The vortex center moves around the bubble, as has been shown before for the case where rotation of the bubble is absent18,19, with the position of the center of the vortex, Fig. 2a, showing several turns and wobbles. Rotation of the cell introduces a global movement of the bubble and the vortex. This movement gives a privileged direction to the vortex trajectory as seen in Fig. 2a for the high rotation frequency. Note that Fig. 2a shows trajectories of vortices both with and without rotation of the bubble. In general, rotation forces the vortex to remain at a restricted latitude as shown in Fig. 2a. By tracking the center of the vortex, the mean and the standard deviation of the latitude of the vortex center can be defined from the meandering of the vortex position around the bubble. As the rotation rate increases, the mean latitude for the presence of the vortices increases, as shown in Fig. 2b, with most observed vortices living between 70 and 90 degrees (i.e. close to the pole) for rotation rates in excess of 0.2 Hz. The inset of Fig. 2b shows that, on average, vortices are more confined for the higher rotation rates as the standard deviation of their latitude becomes smaller when the rotation rate increases. The effect of rotation is thus to privilege vortices near the pole and whose displacement is quite confined. We are not aware of calculations or experiments showing such an effect. A second surprising result is that beyond a certain rotation rate (about 1.8 Hz), vortices simply do not live long enough to be scrutinized. The life time of the vortices is plotted in the inset of Fig. 2b for high rotation rates. This life time can be large for low rotation speeds or for the case with no rotation but decreases for high rotation rates. Again, we are not aware of observations or calculations of this counterintuitive effect. The effects of rotation therefore turn out to be highly non trivial as it suppresses long lifetime vortices and confines them near the pole. Both effects call for additional work to elucidate reasons behind our observations. Numerical simulations of turbulent flows on a rotating sphere24 have however indicated a tendency of single vortices to migrate to the polar region and our experiments seem to be in line with these results. Our sphere is undergoing thermal convection which is not taken into account in these simulations.
Properties of the vortices: (a) Examples of trajectories of the center of the vortex, note that the vortex' center moves in all directions. As the rotation rate increases, the vortex moves towards the pole and deviations from its mean latitude decrease. (b) Latitude of the vortex position versus rotation frequency, for each frequency three representative vortices were selected. Left inset: Standard deviation of vortex latitude versus rotation rate. Right inset: Life times of the vortices for different rotation frequencies.
Besides the effects of rotation on the location and lifetime of the vortices, we have characterized their structure through measurements of their velocity and vorticity profiles. From video imaging, we obtain the velocity field of the vortex, Fig. 3a, using particle imaging velocimetry (PIV). Also, the center location of the vortex as well as the temporal evolution of the position of small thickness inhomogeneities or particles surrounding the vortex can be followed. From such tracks, Fig. 3b, where the trajectory of the tracked inhomogeneities around the eye can be seen, one obtains the azimuthal velocity and the vorticity averaged over one revolution. The tracks of the markers show elliptical trajectories around the center of the vortex once the global movement of the vortex center has been subtracted. The long axis of the elliptical trajectory usually lies along the horizontal direction. The ellipticity of these trajectories indicates that these vortices are elliptical vorticity patches. The ellipticity (the ratio of the long axis to the short axis) of the trajectories is around 1.2 to 1.3. No marked changes of the ellipticity for different rotation frequencies was noted.
Structure of the vortex: (a) The velocity field of a vortex from Particle Imaging Velocimetry. (b) Once the center position has been subtracted from the trajectory of the tracked particles, elliptical trajectories are obtained. Analysis of these trajectories allows to obtain the velocity and the vorticity around the vortex. Four different trajectories at different distances from the center are shown. (c) a zoom on a vortex obtained in our numerical simulations, the color code (given in figure 1) indicates the value of the vorticity. (d) The velocity and vorticity profiles obtained from the full velocity field as shown in a. The solid lines are fits using a Gaussian vortex. The parameters of the fit are given in the graph. (d) Different trajectories (as in b) at different positions from the center allow to obtain the variation of the vorticity and the azimuthal velocity versus radial position. This variation is fit to a Gaussian vortex with parameters given in the graph. (e) Velocity and vorticity profile of the numerical vortex in (c). The solid lines are fits to a Gaussian vortex with parameters given in the graph. The distance scale and the time scale of the numerics are normalized by the radius of the bubble R and by  (g is gravity) respectively.
(g is gravity) respectively.
Examples of velocity and vorticity profiles for a typical vortex are displayed in Fig. 3d and e. The velocity first increases as the distance to the center increases, goes through a maximum, before decaying far away from the center. The velocity does not necessarily decay to zero but rather to the value of the velocity in the far away flow field. Such velocity profiles are typical of a variety of known vortices3. The one examined here can be reasonably approximated by a Gaussian vortex3 as shown by the solid lines in Fig. 3. The azimuthal velocity profile of such a vortex obeys  . Here Γ is the circulation, r is the distance from the center of the vortex and λ is a characteristic length. From the azimuthal velocity we obtain the vorticity profile as ω(r) = V(r)/r + ∂V(r)/∂r (Fig. 3). A fit to the Gaussian functional shape is shown as well and seems to capture the essential features of this vortex. Similar profiles can be obtained from the tracking measurements. Each ellipse gives access to a distance r from the center of the vortex; analysis of different ellipses gives access to the profile. While the profiles (see Fig. 3e) are not as populated as the profiles obtained from the PIV measurements especially near the center and far away from it, the Gaussian shape works reasonably well. The structure of the single vortices obtained numerically mimics that from experiments as shown in Fig. 3c and 3f where the vorticity and the velocity variation versus the distance from the center of the vortex is shown along with a Gaussian vortex fit. The vortices obtained both from the numerical simulations and the experiments are therefore Gaussian vortices. While the profiles shown in Fig. 3 are for the case with no rotation of the bubble, velocity and vorticity profiles in the presence of rotation can also be reasonably approximated with the Gaussian shape. Rotation therefore does not change the structure of the observed vortices.
. Here Γ is the circulation, r is the distance from the center of the vortex and λ is a characteristic length. From the azimuthal velocity we obtain the vorticity profile as ω(r) = V(r)/r + ∂V(r)/∂r (Fig. 3). A fit to the Gaussian functional shape is shown as well and seems to capture the essential features of this vortex. Similar profiles can be obtained from the tracking measurements. Each ellipse gives access to a distance r from the center of the vortex; analysis of different ellipses gives access to the profile. While the profiles (see Fig. 3e) are not as populated as the profiles obtained from the PIV measurements especially near the center and far away from it, the Gaussian shape works reasonably well. The structure of the single vortices obtained numerically mimics that from experiments as shown in Fig. 3c and 3f where the vorticity and the velocity variation versus the distance from the center of the vortex is shown along with a Gaussian vortex fit. The vortices obtained both from the numerical simulations and the experiments are therefore Gaussian vortices. While the profiles shown in Fig. 3 are for the case with no rotation of the bubble, velocity and vorticity profiles in the presence of rotation can also be reasonably approximated with the Gaussian shape. Rotation therefore does not change the structure of the observed vortices.
Besides the characterization of the structure of the observed vortices, we have also made measurements of the azimuthal velocity of the vortex over longer periods of time spanning several turnover times of the vortex. A typical turnover time of these vortices is a fraction of a second (0.1 s). An example of the long time dynamics of the azimuthal velocity is displayed in figure 4a. The time trace is obtained from tracking particles and the velocity and vorticity are obtained from fits to the trajectory of the particles around the center of the vortex as in Fig. 3. Each ellipse gives access to the azimuthal velocity and to the vorticity for a particular location from the center of the vortex and for a particular time period. Note that a long time variation can be observed in these measurements. This long time variation shows periods of constant low velocity and vorticity followed by an intensification period with higher velocities and vorticities. The particle followed in this example remains at approximately the same distance from the center so variation in the velocity is not due to the particle meandering towards the center of the vortex or moving away from it. Since the velocity varies with distance from the center of the vortex, if the particle moves towards or away from the center its velocity may change even if the vortex keeps the same intensity. Changes in the intensity are therefore due to the change of the vortex intensity in this case. The vortex followed here ends up reducing its velocity in the end and practically disapearing in the background flow.
Long time dynamics: (a) Long time evolution of the azimuthal velocity and the vorticity of a single vortex, the upper left inset shows the trajectory with visible trochoidal motion during the intensification phase marked by the red and black dots. The two components of the center position are shown in the lower inset. Note the oscillations (indicative of the trochoidal motion) in the temporal variation of the position coordinates versus time with a period close to a turnover time of the vortex. The cell is not under rotation for this case. (b) Trochoidal motion for a vortex except in this case the rotation rate of the cell was set to 0.6 Hz. Images of the vortex are shown in the figure at different instants during the trochoidal motion. Note the absence of a secondary eye.
Another curious aspect we have observed is that during the intensification period, the trajectory of the center of the vortex shows a trochoidal motion as seen in figure 4a and b: the vortex center wobbles a few times around its mean position. The period of oscillation of the center is roughly one turnover time which is comparable to the oscillation period observed for some tropical cyclones25. This is seen for different vortices (two realizations are shown in figure 4) with the period of trochoidal motion being roughly the same and close to 0.1 s. The link between such trochoidal motion and the intensity of the vortex in our case is not clear since trochoidal motion was observed both for the increasing intensity phase as well as during the decreasing intensity one. Different reasons have been proposed to explain this peculiar feature observed during the motion of some TC25,26,27 including an instability of the core of the vortex26 or the existence of a double vortex structure27 giving rise to a periodic displacement of the vortex core with respect to its periphery. Our own observations do not allow a precise determination of the mechanisms at play here but our velocity measurements seem to exclude the double vortex hypothesis and visualizations of the vortex do not seem to indicate large deformations of the core during this phase (see photos in figure 4b).
Let us come back to the intensification of vortices. In Fig. 5 we show several intensification events from the soap bubble as well as from our numerical simulations. Note that both data sets from five different intensification events in the soap bubble and the three events from the numerics show an intensification period where the velocity increases up to a maximum value we note Vmax followed by a decline in intensity. The time scale in this graph has been shifted, so that Vmax occurs at zero time and normalized by a characteristic time τ while the velocity was normalized by Vmax. A surprising feature of this graph is that through a simple rescaling of the velocity and time axes all the data collapse onto a single universal curve indicating that the intensification shows similar features for different vortices at different bubble rotation rates as well as for vortices from the numerical simulations. The time constant τ used to collapse the data is shown in the inset of this figure and turns out to be roughly 0.07 s for the bubble vortices and for the vortices from the numerical simulations. This time constant seems comparable to a tunover time of these vortices which is roughly 0.1 s. The mechanisms behind the intensification and decline of the vortices are however difficult to decipher. We did note that during the intensification period, the vortex seems to maintain its average position without being swept by the background flow. There are also no apparent changes in the structure of the vortices during the intensification phase. Also, the decline phase seems to be related to the presence of strong background flow which ends up sweeping the vortex away from its original position.
Superposition of intensification events from the bubble vortices and from the numerics: vortex intensity from five different intensification events at a different frequencies (of 0, 0.2 and 0.6 Hz) versus time.
Three intensification events from the numerics (using different grids of 512 × 512, 256 × 256 and 2048 × 2048 for the events 1 to 3 respectively) are also shown. The velocity axis has been normalized by the maximum velocity and the time has been normalized by a characteristic time τ and shifted so that the position of the maximum velocity is at zero. Inset: characteristic time versus maximum velocity for the bubble vortices used in this graph.
Discussion
The experimental system proposed here shows a variety of interesting features concerning the properties of vortices on the surface of the bubble: the existence of long lifetime vortices whose structure is well defined and whose long time dynamics shows intriguing properties such as intensification events and trochoidal motion. There are few if any experiments on spherical shells and apart from comparisons to numerical simulations of flow on rotating shallow water spheres, there are few results we can compare our experiments to. As mentioned above, our experiments show a clear tendency for the vortices to move towards the poles as the rotation rate of the spherical shell increases. This aspect seems to be in agreement with numerical simulations24. Also, the velocity and vorticity profiles of the vortices obtained here seems however to be a standard result in many shallow water experiments where Gaussian shapes have been observed3. However, we are not aware of results (experimental, numerical, or theoretical) on the life time of vortices and the effects of rotation on such a quantity, nor are we aware of previous studies of intensification of model vortices.
While the vortices observed here are quasi two dimensional and therefore very different from natural giant vortices such as Tropical cyclones, some of the properties observed here (trochoidal motion and intensification) are also characteristic of Hurricanes and Typhoons. For the sake of comparison and keeping in mind the differences in mechanisms as well as in the energetics of the vortices here and Tropical cyclones we have examined whether such qualitative similarities can be made more quantitative. In a previous study we had shown that the trajectories of the vortices studied here and that of Tropical cyclones share some quantitative features18,19. A particular feature we have examined here concerns the link between the intensification observed here and that of tropical cyclones. These are the only known vortices for which intensification as observed in our experiments is documented. In Fig. 6a we show the variation of the wind velocity V(t) versus time t for a few hurricanes (data obtained from28). Note that the normalization used above is used here also to superimpose intensification data from different hurricanes. This figure shows that such a normalization works reasonably well for this set of data with time constants (given in the figure) which vary but hover around 6 hours. We went a step further and superimposed data from other hurricanes alongside our data (shown in figure 5 above) in figure 6b. Note that both our data from five different intensification events and the tropical cyclone data show an intensification period where the velocity increases up to a maximum value we note Vmax followed by a decline in intensity. The time scale in this graph has been shifted, as done above so that Vmax occurs at zero time and normalized by a characteristic time τ as in figure 5. The velocity was again normalized by Vmax. The curves from different tropical cyclones, from our vortices and from our numerics are superimposed in this representation suggesting that the variation of the velocity versus time is similar for such very different vortices. In itself this result is perhaps not surprising since many different vortices may show an increase and a decrease in intensity. However, a notable feature is that the characteristic time τ needed to normalize the data turns out to be roughly constant and of order 6 h for TCs and 0.07 s for our vortices as shown in the inset. For the numerics the value of τ is about 0.07 s for the three vortices shown in very good agreement with the experiments. Each system therefore seems to be characterized by a single time constant. While the exact meaning of this time constant is not clear at present, its order of magnitude points to roughly one turnover time for the experiments and the numerics and roughly one turnover time for the tropical cyclones if the radius of hurricane force winds is considered. In order to test whether for tropical cyclones the time constant is robust and not just a coincidence, we have performed a similar analysis on a large ensemble of events. A time constant was obtained from superimposing all the data onto the same graph. The histogram of τ values obtained from an analysis of 171 TCs in the Atlantic and the Pacific basins is shown in the inset to figure 6b. Note that the histogram is well defined suggesting that the value of τ has a mean of 6 h with a standard deviation of about 2 h. Furthermore and in Fig. 6b, we have added data from a compilation of tropical cyclone intensity variation with time (over 56 storms in the Atlantic and 73 storms in the Pacific) obtained from29. The normalization as above of this data set using a time constant of 6 h works reasonably well.
(a) Intensification for several hurricanes in the North Eastern pacific. Here again the time and velocity axis have been normalized as in figure 5.The time constants are given along with the name of the TC in the figure. (b) hurricane intensity (from five different hurricanes in the Atlantic as well as two compilations extracted from29 for the Atlantic and Pacific oceans) and vortex intensity (five different intensification events at a frequency of 0, 0.2 and 0.6 Hz) versus time. Three intensification events from the numerics (using different grids of 512 × 512, 256 × 256 and 2048 × 2048 for the events 1 to 3 respectively) are also shown. The velocity axis has been normalized by the maximum velocity and the time has been normalized by a characteristic time τ and shifted so that the position of the maximum velocity is at zero. The left inset shows the characteristic time versus maximum velocity for the intensification events shown in the main figure and for a few additional hurricanes (Georges 1998, Bill 2009, Rita 2005, Katrina 2005, Beta 2005, Helene 2006, Paloma 2008, Dolly 2008, Omar 2008, Isaac 2006, Earl 2010). The right inset shows the linear relation between intensification rate and maximum velocity for a dozen hurricanes (different from the ones used in the left inset): Opal 1995, Andrew 1992, Hugo 1989, Dean 1989, Gilbert 1988, Gloria 1985, Camille 1969, Igor 2010, Gordon 2006, Florence 2006, Dean 2007, Chris 1994. The bottom inset shows a histogram of the time τ obtained from an analysis of 171 tropical cyclones in the Atlantic and the Pacific oceans. The mean value of τ is 6 hours with a standard deviation of 1.8 hours.
The superposition of the data shown in Fig. 6b suggests a simple relation for the variation of the wind speed versus time:  or equivalently
or equivalently  for the increase and the decrease in intensity before and after tmax. Note however that there are deviations for t > tmax (see Katrina case in Fig. 6b) when the hurricane approaches landfall and the intensity decreases fast. From this relation, the maximum attainable wind speed Vmax is directly related to the rate of change of the velocity during the intensification period. Separate estimates of the velocity rate of change
for the increase and the decrease in intensity before and after tmax. Note however that there are deviations for t > tmax (see Katrina case in Fig. 6b) when the hurricane approaches landfall and the intensity decreases fast. From this relation, the maximum attainable wind speed Vmax is directly related to the rate of change of the velocity during the intensification period. Separate estimates of the velocity rate of change  and the maximum speed Vmax comfort this relation as seen in the inset of Fig. 6b. Furthermore and since the temporal variation of the velocity turns out to be roughly linear, the duration of the intensification period or tmax can be determined as it lasts 16τ. Note that the mechanisms at play in the intensification of vortices here and of tropical cyclones are very different since our vortices are quasi two dimensional and prone mostly to interactions with the background flow while tropical cyclones have a full and complex three dimensional structure. The collapse of the data shown here is therefore not indicative of mechanisms that are similar. We recall that different mechanisms have been proposed for the intensification of tropical cyclones and which stress different aspects such as the thermodynamic profile of the atmosphere and upper ocean, the interplay between evaporation from the ocean and the dissipation in the storm's atmospheric boundary layer, the role of vortical convective plumes, among others7,12,13. For the soap film vortices, the role of thermal plumes and the surrounding flow may be important. A major difference between tropical cyclone intensification mechanisms and possible mechanisms in the soap film is their three dimensional nature in the first case and the two dimensional nature in the second case. Nonetheless, the collapse of the data proposed here may indicate that the dynamics of the intensification of vortices may have generic features which may be useful in the understanding of such a difficult problem.
and the maximum speed Vmax comfort this relation as seen in the inset of Fig. 6b. Furthermore and since the temporal variation of the velocity turns out to be roughly linear, the duration of the intensification period or tmax can be determined as it lasts 16τ. Note that the mechanisms at play in the intensification of vortices here and of tropical cyclones are very different since our vortices are quasi two dimensional and prone mostly to interactions with the background flow while tropical cyclones have a full and complex three dimensional structure. The collapse of the data shown here is therefore not indicative of mechanisms that are similar. We recall that different mechanisms have been proposed for the intensification of tropical cyclones and which stress different aspects such as the thermodynamic profile of the atmosphere and upper ocean, the interplay between evaporation from the ocean and the dissipation in the storm's atmospheric boundary layer, the role of vortical convective plumes, among others7,12,13. For the soap film vortices, the role of thermal plumes and the surrounding flow may be important. A major difference between tropical cyclone intensification mechanisms and possible mechanisms in the soap film is their three dimensional nature in the first case and the two dimensional nature in the second case. Nonetheless, the collapse of the data proposed here may indicate that the dynamics of the intensification of vortices may have generic features which may be useful in the understanding of such a difficult problem.
Methods
Set up description: The set up is composed of different parts and is shown in Fig. 1a. An inner brass disk (1) on which the half bubble is blown and an outer annulus (2) to heat up this brass disk and therefore heat up the soap solution contained in the circular hollow groove (3) on the inner brass disk. The outer annulus and the inner brass disk are not in contact with each other but are spaced by less than a millimeter to facilitate the heating. The outer annulus is hollow and water circulating within this annulus and heated using a water circulation bath allows to fix the temperature of this annulus. The immediate proximity of the inner brass disk and the soap solution contained in the groove to this heated outer annulus helps fix the temperature of the soap water and therefore the base of the bubble in contact with the soap water in the groove. The inner brass disk and therefore the whole half bubble can be rotated using a continuous motor (6) connected to the inner disk with a shaft (5). The bubble is blown using the solution (water + 1% detergent (Fairy Dreft by Procter & Gamble)) in the groove. The water in the groove is heated through the heating of the inner disk by the outer annulus. The middle section of the inner disk is covered with a thick (2 mm) Teflon coating (4) to minimize the heating of the air inside the bubble. The cell dimensions allow to make half bubbles with a 12 cm diameter (i.e. the diameter of the groove). The temperature at the equator of the bubble is set by the temperature of the water circulation bath. This temperature can be varied from 30 to 90°C. In principle, only the base of the bubble in contact with the soap water in the groove is heated. It is this heating at the base of the bubble which generates thermal convection on the bubble surface. For the results shown here, the temperature of the bath was fixed to 55°C. For such a temperature, the probability of obtaining vortices is reasonably large and their life time can be long enough. Measurements done at other temperature did not show much change in the characteristics of the vortices described here. The whole cell can be set in motion around the central axis introducing a rotation frequency f which can be varied between 0.1 and 3 Hz. The schematic of figure 1a gives a full description of the set up. The images are taken in reflection, using a fast color camera working at rates up to 500 frames per second, of white light so the colors represent interference fringes and therefore thickness variations of the thin membrane constituting the bubble.
References
Hu, D. L., Chan, B. & Bush, J. W. M. The hydrodynamics of water strider locomotion. Nature 424, 663 (2003).
Marcus, P. S. Numerical simulation of Jupiter's Great Red Spot. Nature 331, 693 (1988).
Green, S. I. Fluid Vortices, (Kluwer Academic Publishers, The Netherlands, 1995).
Frisch, U. Turbulence: The Legacy of Kolmogorov, (Cambridge University Press, Cambridge, UK, 1995).
Polvani, L. M., Wisdom, J., Dejong, E. & Ingersoll, A. P. Simple dynamical models of Neptune's great dark spot. Science 249, 1393 (1990).
Chan, J. C. L. & Kepert, J. D. Global Perspectives on Tropical Cyclones, (World Scientific Publishing Co. 2010).
Emanuel, K. E. Tropical Cyclones. Annu. Rev. Earth and Planet. Sci. 31, 75 (2003).
Liu, T., Wang, B. & Choi, D. S. Flow structures of Jupiter's Great Red Spot extracted by using optical flow method. Phys. Fluids 24, 096601 (2012).
Choi, D. S., Banfield, D., Gierasch, P. & Showman, A. P. Velocity and vorticity measurements of Jupiter's Great Red Spot using automated cloud feature tracking. Icarus 188, 35 (2007).
Mallen, K. J., Montgomery, M. T. & Wang, B. Reexamining the near-core radial structure of the tropical cyclone primary circulation: Implications for vortex resiliency. J. Atmos. Sci. 62, 408 (2005).
Holland, G. J., Belanger, J. I. & Fritz, A. A Revised model for radial profiles of Hurricane winds. Monthly Weather Review 138, 4393 (2010).
Emanuel, K. E. Thermodynamic control of hurricane intensity. Nature 401, 665 (1999).
Montgomery, M. T. & Smith, R. K. Paradigms for tropical-cyclone intensification. Australian Meteorological and Oceanographical Journal, (in press).
Ooyama, K. Numerical simulation of the life cycle of tropical cyclones. J. Atmos. Sci. 26, 3 (1969).
Smith, R. K., Schmidt, C. W. & Montgomery, M. T. An investigation of rotational influences on tropical-cyclone size and intensity. Q. J. R. Meteorol. Soc. 137, 1841 (2011).
Sommeria, J., Meyers, S. D. & Swinney, H. L. Laboratory model of a planetary eastward jet. Nature 337, 58 (1989).
Solomon, T. H., Holloway, W. J. & Swinney, H. L. Shear flow instabilities and Rossby waves in barotropic flow in a rotating annulus. Phys. Fluids 5, 1971 (1993).
Seychelles, F., Amarouchene, Y., Bessafi, M. & Kellay, H. Thermal convection and emergence of isolated vortices in soap bubbles. Phys. Rev. Lett. 100, 144501 (2008).
Meuel, T., Prado, G., Seychelles, F., Bessafi, M. & Kellay, H. Hurricane track forecast cones from fluctuations. Scientific. Reports. 2, 446, 10.1038/srep00446 (2012).
Xia, H., Byrne, D., Falkovich, G. & Shats, M. Upscale energy transfer in thick turbulent fluid layers. Nature Physics 7, 321 (2011).
Turner, J. S. & Lilly, D. K. The carbonated-water tornado vortex. J. Atmos. Sci. 20, 468 (1963).
Seychelles, F., Ingremeau, F., Pradere, J. C. & Kellay, H. From intermittent to nonintermittent behavior in two dimensional thermal convection in a soap bubble. Phys. Rev. Lett. 105, 264502 (2010).
Xiong, Y.-L., Fischer, P. & Bruneau, C. H. Numerical simulations of two-dimensional turbulent thermal convection on the surface of a soap bubble, paper presented at Intern. Conf. Comput. Fluid Dynamics Proceedings, Hawaii (July 9–13, 2012), ICCFD7-3703. The paper is accessible at http://www.iccfd.org/iccfd7/proceedings.html.
Cho, J. Y. K. & Polvani, L. M. The energence of jets and vortices in freely evolving, shallowwater turbulence on a sphere. Phys. Fluids 8, 1531 (1996).
Lawrence, M. B. & Mayfield, B. M. Satellite observations of trochoidal motion during hurricane Belle 1976. Monthly Weather Review 105, 1458 (1977).
Nolan, D., Montgomery, M. T. & Grasso, T. The wavenumber-one instability and trochoidal motion of hurricane like vortices. J. Atmos. Sci. 58, 3233 (2001).
Oda, M., Nakanishi, M. & Naito, G. Interaction of an Asymmetric Double Vortex and Trochoidal Motion of a Tropical Cyclone with the Concentric Eyewall Structure. J. Atmos. Sci. 63, 1069 (2006).
The National Hurricane Center web site: http://www.nhc.noaa.gov, last accessed on the 5th of March 2013.
Emanuel, K. E. A statistical analysis of tropical cyclone intensity. Monthly Weather Review 128, 1139 (2000).
Acknowledgements
This work was funded by an ANR grant ‘Cyclobulle’. We thank S. Bosio for help with the experimental set up and J. Vigh for discussions.
Author information
Authors and Affiliations
Contributions
H.K. designed the experiment, T.M. carried out the experiments, T.M. and H.K. analyzed data. Y.L.X., P.F. and C.H.B. carried out the numerical simulations. M.B. provided hurricane data and contributed to the analysis. H.K. wrote the paper with input from all authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Meuel, T., Xiong, Y., Fischer, P. et al. Intensity of vortices: from soap bubbles to hurricanes. Sci Rep 3, 3455 (2013). https://doi.org/10.1038/srep03455
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03455
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.