Abstract
Fermi liquid theory is remarkably successful in describing the transport and optical properties of metals; at frequencies higher than the scattering rate, the optical conductivity adopts the well-known power law behavior σ1(ω) ∝ ω−2. We have observed an unusual non-Fermi liquid response σ1(ω) ∝ ω−1±0.2 in the ground states of several cuprate and iron-based materials which undergo electronic or magnetic phase transitions resulting in dramatically reduced or nodal Fermi surfaces. The identification of an inverse (or fractional) power-law behavior in the residual optical conductivity now permits the removal of this contribution, revealing the direct transitions across the gap and allowing the nature of the electron-boson coupling to be probed. The non-Fermi liquid behavior in these systems may be the result of a common Fermi surface topology of Dirac cone-like features in the electronic dispersion.
Similar content being viewed by others
Introduction
In a Fermi liquid, the complex conductivity  can be expressed through the generalized Drude model,
can be expressed through the generalized Drude model,  (in units of Ω−1cm−1), where
(in units of Ω−1cm−1), where  and 1 + λ(ω) = m*(ω)/mb are the plasma frequency, frequency-dependent scattering rate and mass enhancement, respectively, where n is a carrier concentration and mb is the band mass. At low-temperature the scattering rate will vary quadratically with frequency and temperature,
and 1 + λ(ω) = m*(ω)/mb are the plasma frequency, frequency-dependent scattering rate and mass enhancement, respectively, where n is a carrier concentration and mb is the band mass. At low-temperature the scattering rate will vary quadratically with frequency and temperature,  , where A is a constant that varies with the material1,2. In the frequency domain, for
, where A is a constant that varies with the material1,2. In the frequency domain, for  the conductivity varies slowly, but for
the conductivity varies slowly, but for  the conductivity adopts a power-law behavior, σ1 ∝ ω−2; however, deviations from this behavior may be observed in strongly-correlated electronic systems3,4,5,6,7.
the conductivity adopts a power-law behavior, σ1 ∝ ω−2; however, deviations from this behavior may be observed in strongly-correlated electronic systems3,4,5,6,7.
Results
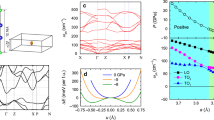
The temperature dependence of the optical conductivity of optimally-doped Bi2Sr2CaCu2O8+δ, one of the most thoroughly studied cuprate high-temperature superconductors8, is shown versus wave number (photon energy) in a log-log plot in Fig. 1a for light polarized along the crystallographic a axis9. Just above Tc it may be argued that the optical properties are consistent with those of a Fermi liquid (see Supplementary Information and Fig. S1 online for a discussion of different models for the optical conductivity and the frequency-dependent scattering rate); this statement is in keeping with the proposed phase diagram for the high-temperature superconductors10. Below Tc there is a rapid reduction of the low-frequency conductivity or spectral weight, which is defined as the area under the conductivity curve; this ‘missing spectral weight’ is the optical signature for the formation of a superconducting condensate8. However, even down to the lowest measured temperature there is still a significant amount of low-frequency residual conductivity11. This is because, unlike a conventional s-wave superconductor in which the entire Fermi surface is completely gapped below Tc, the cuprate materials have a momentum-dependent d-wave gap that contains nodes12,13, Δ(k) = Δ0 [cos(kxa) − cos(kya)], where Δ0 is the gap maximum. The presence of nodes allows pair-breaking out of the superconducting state resulting in unpaired nodal quasiparticles14. For low photon energies ( ) only the nodal structure of the d-wave gap is probed and the Fermi surface topology is similar to that of the Dirac cone observed in graphene and other quantum materials15,16. The rapid collapse of the quasiparticle scattering rate17 below Tc indicates that in the far-infrared region
) only the nodal structure of the d-wave gap is probed and the Fermi surface topology is similar to that of the Dirac cone observed in graphene and other quantum materials15,16. The rapid collapse of the quasiparticle scattering rate17 below Tc indicates that in the far-infrared region  , so σ1 ∝ ω−2 should be clearly revealed. Surprisingly, what is observed instead is that below Tc low-frequency residual optical conductivity forms a family of lines with the same non-Fermi liquid fractional power law behavior σ1 ∝ ω−1.2; in metallic systems at low-frequency where
, so σ1 ∝ ω−2 should be clearly revealed. Surprisingly, what is observed instead is that below Tc low-frequency residual optical conductivity forms a family of lines with the same non-Fermi liquid fractional power law behavior σ1 ∝ ω−1.2; in metallic systems at low-frequency where  , this is approximately equivalent to the scattering rate having a fractional power law behavior 1/τ ∝ ω1.2. Another family of cuprates that has been extensively investigated are the YBa2Cu3O6+y materials. The optical conductivity of optimally-doped YBa2Cu3O6.95 is shown in Fig. 1b for light polarized along the a axis; this crystallographic axis is transverse to the copper-oxygen chains and should therefore probe the dynamics of only the copper-oxygen planes18. Well below Tc, the observed power law for the residual conductivity σ1 ∝ ω−1.2 is identical to the response observed in optimally-doped Bi2Sr2CaCu2O8+δ. The underdoped YBa2Cu3O6.60 sample is of particular interest due to the formation of a pseudogap in the normal state19 and the commensurate reduction of the Fermi surface around the nodal regions, a condition that has been referred to as a ‘nodal metal’20,21. The optical conductivity for this material is shown in Fig. 1c for light polarized along the a axis. Just above Tc in the normal state the low-frequency optical conductivity may be described using a non-Fermi liquid power-law, σ1 ∝ ω−0.85; however, what is fascinating is that well below Tc the response of the unpaired quasiparticles displays the identical fractional power law. This indicates the (unpaired) quasiparticles appear to behave the same way regardless of whether it is the pseudogap that results in the reduction of a large Fermi surface to a small arc or pocket22, or the formation of a d-wave superconducting energy gap resulting in nodes. This non-Fermi liquid power-law behavior in the underdoped material has been previously observed in the microwave region23; however, in that work the exponent is considerably larger, σ1 ∝ ω−1.45. The most likely source for this disagreement is the fact that the microwave experiments are done in the ωτ ~ 1 region, while the optical work was performed in the
, this is approximately equivalent to the scattering rate having a fractional power law behavior 1/τ ∝ ω1.2. Another family of cuprates that has been extensively investigated are the YBa2Cu3O6+y materials. The optical conductivity of optimally-doped YBa2Cu3O6.95 is shown in Fig. 1b for light polarized along the a axis; this crystallographic axis is transverse to the copper-oxygen chains and should therefore probe the dynamics of only the copper-oxygen planes18. Well below Tc, the observed power law for the residual conductivity σ1 ∝ ω−1.2 is identical to the response observed in optimally-doped Bi2Sr2CaCu2O8+δ. The underdoped YBa2Cu3O6.60 sample is of particular interest due to the formation of a pseudogap in the normal state19 and the commensurate reduction of the Fermi surface around the nodal regions, a condition that has been referred to as a ‘nodal metal’20,21. The optical conductivity for this material is shown in Fig. 1c for light polarized along the a axis. Just above Tc in the normal state the low-frequency optical conductivity may be described using a non-Fermi liquid power-law, σ1 ∝ ω−0.85; however, what is fascinating is that well below Tc the response of the unpaired quasiparticles displays the identical fractional power law. This indicates the (unpaired) quasiparticles appear to behave the same way regardless of whether it is the pseudogap that results in the reduction of a large Fermi surface to a small arc or pocket22, or the formation of a d-wave superconducting energy gap resulting in nodes. This non-Fermi liquid power-law behavior in the underdoped material has been previously observed in the microwave region23; however, in that work the exponent is considerably larger, σ1 ∝ ω−1.45. The most likely source for this disagreement is the fact that the microwave experiments are done in the ωτ ~ 1 region, while the optical work was performed in the  limit, suggesting that the relaxation processes in these two regimes may be different. Surprisingly, recent results on the single-layer, underdoped cuprate HgBa2CuO4+δ demonstrate that it displays Fermi liquid-like behavior24, indicating that the nature of the underdoped (pseudogap) region in the cuprate materials is still controversial.
limit, suggesting that the relaxation processes in these two regimes may be different. Surprisingly, recent results on the single-layer, underdoped cuprate HgBa2CuO4+δ demonstrate that it displays Fermi liquid-like behavior24, indicating that the nature of the underdoped (pseudogap) region in the cuprate materials is still controversial.
The optical conductivity of some quantum materials.
(a), The temperature dependence of the optical conductivity versus wave number (photon energy) for optimally-doped Bi2Sr2CaCu2O8+δ (Tc = 91 K) for light polarized along the crystallographic a axis. At low frequency just above Tc the material may be cautiously described as a Fermi liquid. For all the temperatures measured below Tc the residual conductivity from the unpaired quasiparticles follows the same non-Fermi liquid fractional power law, σ1(ω) ∝ ω−1.2. (b), The plot for optimally-doped YBa2Cu3O6.95 (Tc = 91 K), for light polarized along the a axis, illustrating the fractional power law below Tc. (c), The plot for underdoped YBa2Cu3O6.60 ( ), for light polarized along the a axis, illustrating an identical (non-Fermi liquid) fractional power-law behavior in the normal (pseudogap) and superconducting states. (d), The plot for the BaFe2As2 (TSDW = 138 K), for light polarized in the a–b planes. Below TSDW the fractional power law σ1 ∝ ω−1.2 is again observed.
), for light polarized along the a axis, illustrating an identical (non-Fermi liquid) fractional power-law behavior in the normal (pseudogap) and superconducting states. (d), The plot for the BaFe2As2 (TSDW = 138 K), for light polarized in the a–b planes. Below TSDW the fractional power law σ1 ∝ ω−1.2 is again observed.
Interestingly, an almost identical behavior has also been observed in the AFe2As2 (A = Ba and Ca) iron-arsenic compounds25. In BaFe2As2 a spin-density-wave (SDW) state develops below  , resulting in the formation of a Dirac-like cone in the electronic dispersion close to the Fermi surface26,27 with small pockets or puddles. The frequency-dependent scattering rate has a clear quadratic component just above TSDW, suggesting the non-magnetic state of this material may be described as a Fermi liquid (see Supplementary Fig. S2a online); when the SDW transition is removed by Co substitution, the quadratic behavior persists from 295 K down to 27 K (see Supplementary Fig. S2b online). The optical conductivity of BaFe2As2 is shown in Fig. 1d; for
, resulting in the formation of a Dirac-like cone in the electronic dispersion close to the Fermi surface26,27 with small pockets or puddles. The frequency-dependent scattering rate has a clear quadratic component just above TSDW, suggesting the non-magnetic state of this material may be described as a Fermi liquid (see Supplementary Fig. S2a online); when the SDW transition is removed by Co substitution, the quadratic behavior persists from 295 K down to 27 K (see Supplementary Fig. S2b online). The optical conductivity of BaFe2As2 is shown in Fig. 1d; for  we once again observe the fractional power law in the residual low-frequency optical conductivity28, σ1 ∝ ω−1.2, similar to that seen in the ground state of several of the cuprates. The identical power law is also observed in CaFe2As2 for
we once again observe the fractional power law in the residual low-frequency optical conductivity28, σ1 ∝ ω−1.2, similar to that seen in the ground state of several of the cuprates. The identical power law is also observed in CaFe2As2 for  (see Supplementary Fig. S3 online).
(see Supplementary Fig. S3 online).
Discussion
One important aspect of the fractional power law lies in its ability to remove the nodal quasiparticle (residual) response that masks the gap. In a superconductor, the real part of the optical conductivity at low frequencies may be expressed as the linear combination  , where δ(0) is the zero-frequency component that corresponds to the superfluid density, σqp is the conductivity due to the unpaired quasiparticles and σgap is the contribution due to direct excitations across the gap. [In the normal state, δ(0) is absent and σqp is just the quasiparticle response from the whole Fermi surface.] Because we now have an explicit functional form for σqp for various materials, then for ω > 0 we neglect δ(0) and the low-frequency response is
, where δ(0) is the zero-frequency component that corresponds to the superfluid density, σqp is the conductivity due to the unpaired quasiparticles and σgap is the contribution due to direct excitations across the gap. [In the normal state, δ(0) is absent and σqp is just the quasiparticle response from the whole Fermi surface.] Because we now have an explicit functional form for σqp for various materials, then for ω > 0 we neglect δ(0) and the low-frequency response is  . The conductivity due to the superconducting energy gap may be described phenomenologically using a Kubo-Greenwood approach29 in which all the zero-momentum transitions across the gap in the Brillouin zone are considered; in general terms, the optical conductivity due to the gap is a reflection of the joint density of states of the photo-excited electron and hole pairs. In a conventional superconductor with an isotropic energy gap Δ and weak coupling to phonons (or any other exchange boson), then for
. The conductivity due to the superconducting energy gap may be described phenomenologically using a Kubo-Greenwood approach29 in which all the zero-momentum transitions across the gap in the Brillouin zone are considered; in general terms, the optical conductivity due to the gap is a reflection of the joint density of states of the photo-excited electron and hole pairs. In a conventional superconductor with an isotropic energy gap Δ and weak coupling to phonons (or any other exchange boson), then for  in systems at or close to the dirty limit
in systems at or close to the dirty limit  , the onset of absorption will occur at 2Δ; for modest coupling, this onset shifts to Ω0 + 2Δ, where Ω0 is the energy of the boson30,31. Similarly, in a d-wave superconductor in the dirty limit with weak coupling, the onset would be expected at
, the onset of absorption will occur at 2Δ; for modest coupling, this onset shifts to Ω0 + 2Δ, where Ω0 is the energy of the boson30,31. Similarly, in a d-wave superconductor in the dirty limit with weak coupling, the onset would be expected at  ; however, for moderate coupling the onset should shift to Ω0 with a local maximum at
; however, for moderate coupling the onset should shift to Ω0 with a local maximum at  .
.
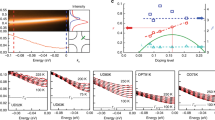
The result for the removal of the quasiparticle contribution, σ1(ω) − σqp, is shown in Fig. 2 for Bi2Sr2CaCu2O8+δ at ~6 K, well below Tc the resulting conductivity is effectively zero at low frequency and the onset of conductivity does not begin until  . This corresponds to the bosonic excitation at Ω0, the frequency above which a change occurs in the optical conductivity due to the strong renormalization of the scattering rate (see Fig. 1a). This indicates that there is at least moderate electron-boson coupling in this material32,33 and that the local maximum in the conductivity will be at
. This corresponds to the bosonic excitation at Ω0, the frequency above which a change occurs in the optical conductivity due to the strong renormalization of the scattering rate (see Fig. 1a). This indicates that there is at least moderate electron-boson coupling in this material32,33 and that the local maximum in the conductivity will be at  . The inferred values of
. The inferred values of  and
and  are in good agreement with estimates for these quantities based from angle-resolved photoemission spectroscopy13 and are consistent with optical inversion techniques9,34. This procedure may also be successfully applied to the YBa2Cu3O6+y materials (see Supplementary Fig. S4 online), as well as the iron-based BaFe2As2 and CaFe2As2 materials in their SDW states (see Supplementary Fig. S5 online).
are in good agreement with estimates for these quantities based from angle-resolved photoemission spectroscopy13 and are consistent with optical inversion techniques9,34. This procedure may also be successfully applied to the YBa2Cu3O6+y materials (see Supplementary Fig. S4 online), as well as the iron-based BaFe2As2 and CaFe2As2 materials in their SDW states (see Supplementary Fig. S5 online).
The decomposition of the optical conductivity in a cuprate superconductor.
The optical conductivity of optimally-doped Bi2Sr2CaCu2O8+δ at 6 K versus wave number (photon energy) with the residual quasiparticle conductivity shown and removed; several sharp features in the conductivity have been fit to Lorentzian oscillators (Supplementary Information) and have also been removed. The subtracted spectra shows an onset of absorption at Ω0 and a local maximum at  .
.
The significance of our finding is the common fractional power law behavior of the low-frequency optical conductivity (THz and far-infrared regions) in materials with Dirac cone-like electronic dispersion and nodal Fermi surfaces. More generally, the fractional power law behavior signals the importance of many-body effects in quantum materials with this unique electronic dispersion, where the fractional power law in conductivity is roughly equivalent to a nearly-linear frequency dependence of the scattering rate. Similar results have been found in single layer graphene in the linear dependence of the resistivity which is the result of electron-phonon (acoustic phonon) coupling35. However, in the materials discussed here, the electron-phonon coupling is weak. The power-law behavior observed in this work is likely the result of the scattering of nodal quasiparticles by low-energy (bosonic) excitations, or possibly some unique self-energy effect of the Dirac-like quasiparticles. What is common for these systems are the existence of antiferromagnetic spin fluctuations (or over-damped spin density waves in the SDW materials), which may be the underlying mechanism that gives rise to the nearly linear frequency dependence of the scattering rate.
Methods
The temperature dependence of the absolute reflectance was measured at a near-normal angle of incidence over a wide frequency range using an in situ evaporation method36. In this study mirror-like as-grown crystal faces have been examined. The complex optical properties were determined from a Kramers-Kronig analysis of the reflectance37. The Kramers-Kronig transform requires that the reflectance be determined for all frequencies, thus extrapolations must be supplied in the ω → 0, ∞ limits. In the metallic state the low frequency extrapolation follows the Hagen-Rubens form,  , while in the superconducting state R(ω) ∝ 1 − ω4 is typically employed; however, it should be noted that when the reflectance is close to unity the analysis is not sensitive upon the choice of low-frequency extrapolation. The reflectance is assumed to be constant above the highest measured frequency point up to
, while in the superconducting state R(ω) ∝ 1 − ω4 is typically employed; however, it should be noted that when the reflectance is close to unity the analysis is not sensitive upon the choice of low-frequency extrapolation. The reflectance is assumed to be constant above the highest measured frequency point up to  , above which a free electron gas asymptotic reflectance extrapolation R(ω) ∝ 1/ω4 is employed38.
, above which a free electron gas asymptotic reflectance extrapolation R(ω) ∝ 1/ω4 is employed38.
References
Gurzhi, R. N. Some features of the electrical conductivity of metals at low temperatures. Soviet Physics JETP 20, 953–960 (1965).
Nagel, U. et al. Optical spectroscopy shows that the normal state of URu2Si2 is an anomalous Fermi liquid. PNAS 109, 19161–19165 (2012).
van der Marel, D. Anisotropy of the optical conductivity of high-Tc cuprates. Phys. Rev. B 60, R765–R768 (1999).
Dodge, J. S. et al. Low-frequency crossover of the fractional power-law conductivity in SrRuO3 . Phys. Rev. Lett. 85, 4932–4935 (2000).
Orenstein, J. & Millis, A. J. Advances in the physics of high-temperature superconductivity. Science 288, 468–474 (2000).
Dordevic, S. V. & Basov, D. N. Electrodynamics of correlated electron matter. Ann. Phys. 15, 545–570 (2006).
Berthod, C. et al. Non-Drude universal scaling laws for the optical response of local Fermi liquids. Phys. Rev. B 87, 115109 (2013).
Basov, D. N. & Timusk, T. Electrodynamics of high-Tc superconductors. Rev. Mod. Phys. 77, 721–779 (2005).
Tu, J. J., Homes, C. C., Gu, G. D., Basov, D. N. & Strongin, M. Optical studies of charge dynamics in optimally doped Bi2Sr2CaCu2O8+δ . Phys. Rev. B 66, 144514 (2002).
Broun, D. M. What lies beneath the dome? Nat. Phys. 4, 170–172.
Buckley, R. G., Barowski, H. S. & Renk, K. F. Far-infrared measurement of the dopant-dependent residual absorptivity of Bi2Sr2CaCu2O8+δ . Phys. Rev. B 64, 014509 (2001).
Van Harlingen, D. J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—Evidence for symmetry. Rev. Mod. Phys. 67, 515–535 (1995).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Lee, P. A. Localized states in a d-wave superconductor. Phys. Rev. Lett. 71, 1887–1890 (1993).
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).
Shibauchi, T. et al. In-plane microwave conductivity and quasiparticle scattering rate of superconducting high-Tc cuprates. J. Phys. Soc. Jpn. 65, 3266–3273 (1996).
Homes, C. C. et al. Effect of Ni impurities on the optical properties of YBa2Cu3O6+y . Phys. Rev. B 60, 9782–9792 (1999).
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Ando, Y., Lavrov, A. N., Komiya, S., Segawa, K. & Sun, X. F. Mobility of the doped holes and the antiferromagnetic correlations in underdoped High- Tc cuprates. Phys. Rev. Lett. 87, 017001 (2001).
Lee, Y. S. et al. Electrodynamics of the nodal metal state in weakly doped high-Tc cuprates. Phys. Rev. B 72, 054529 (2005).
Kanigel, A. et al. Evolution of the pseudogap from Fermi arcs to the nodal liquid. Nature Phys. 2, 447–451 (2006).
Turner, P. J. et al. Observation of weak-limit quasiparticle scattering via broadband microwave spectroscopy of a d-wave superconductor. Phys. Rev. Lett. 90, 237005 (2003).
Mirzaei, S. I. et al. Spectroscopic evidence for Fermi liquid-like energy and temperature dependence of the relaxation rate in the pseudogap phase of the cuprates. PNAS 110, 5774–5778 (2013).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Zabolotnyy, V. B. et al. (π, π) electronic order in iron arsenide superconductors. Nature 457, 569–572 (2009).
Richard, P. et al. Observation of dirac cone electronic dispersion in BaFe2As2 . Phys. Rev. Lett. 104, 137001 (2010).
Hu, W. Z. et al. Origin of the spin density wave instability in AFe2As2 (A = Ba, Sr) as revealed by optical spectroscopy. Phys. Rev. Lett. 101, 257005 (2008).
Harrison, W. A. Solid State Theory (McGraw-Hill, New York, 1970).
Akis, R., Carbotte, J. P. & Timusk, T. Superconducting optical conductivity for arbitrary temperature and mean free path. Phys. Rev. B 43, 12804–12808 (1991).
Nicol, E. J., Carbotte, J. P. & Timusk, T. Optical conductivity in high-Tc superconductors. Phys. Rev. B 43, 473–479 (1991).
Carbotte, J. P., Schachinger, E. & Basov, D. N. Coupling strength of charge carriers to spin fluctuations in high-temperature superconductors. Nature 401, 354–356 (1999).
Munzar, D., Bernhard, C. & Cardona, M. Does the peak in the magnetic susceptibility determine the in-plane infrared conductivity of YBCO? A theoretical study. Physica C 312, 121–135 (1999).
Dordevic, S. V. et al. Extracting the electron-boson spectral function α2F(ω) from infrared and photoemission data using inverse theory. Phys. Rev. B 71, 104529 (2005).
Bolotin, K. I., Sikes, K. J., Hone, J., Stormer, H. L. & Kim, P. Temperature-dependent transport in suspended graphene. Phys. Rev. Lett. 101, 096802 (2008).
Homes, C. C., Reedyk, M., Crandles, D. A. & Timusk, T. Technique for measuring the reflectance of irregular, submillimeter-sized samples. Appl. Opt. 32, 2976–2983 (1993).
Dressel, M. & Grüner, G. Electrodynamics of Solids (Cambridge University Press, Cambridge, 2001).
Wooten, F. Optical Properties of Solids (Academic Press, New York, 1972).
Acknowledgements
The authors would like to acknowledge useful discussions with P.W. Anderson, Y.M. Dai, D.N. Basov, D.A. Bonn, S.V. Borisenko, G. Kotliar, P. Phillips, J.D. Rameau, D. Schmeltzer and C. Varma. Research supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Contract No. DE-AC02-98CH10886. C.C.H. would like to acknowledge the hospitality of the Theory Institute for Strongly Correlated and Complex Systems.
Author information
Authors and Affiliations
Contributions
C.C.H. supervised the project and wrote the manuscript and performed the optical measurements on hole-doped YBa2Cu3O6+y and electron-doped Pr1.85Ce0.15CuO4. J.J.T. supervised part of the project, measured the optical properties of Bi2Sr2CaCu2O8+δ and BaFe1.85Co0.15As2 and wrote part of the manuscript. G.D.G. synthesized single crystals of Bi2Sr2CaCu2O8+δ. A.A. measured the optical properties of BaFe2As2 and CaFe2As2; J.L. assisted with the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Homes, C., Tu, J., Li, J. et al. Optical conductivity of nodal metals. Sci Rep 3, 3446 (2013). https://doi.org/10.1038/srep03446
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03446
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.