Abstract
The conversion between enhancement and suppression in six-wave mixing (SWM) and fluorescence signals by phase modulation has demonstrated for the first time. It is observed in our experiment the suppression of SWM and fluorescence is transformed into enhancement in company with the switch from electromagnetically induced transparency (EIT) to electromagnetically induced absorption (EIA) in the transmitted probe with the relative phase changed from 0 to π/2. Our research could be potentially applied in optical communication and quantum information processing.
Similar content being viewed by others
Introduction
Lots of studies focus on the electromagnetically induced transparency (EIT) and the higher-order nonlinear optical process comprising four-wave mixing (FWM) and six-wave mixing (SWM) under EIT condition1,2,3. In the meantime, the fluorescence owing to spontaneous emission is also observed4,5,6. Moreover, the enhancement and suppression of FWM (SWM) and fluorescence corresponding to electromagnetically induced absorption (EIA) and EIT has aroused much interest7,8. The switch between bright state (EIA in the transmitted probe signal and enhancement in FWM and fluorescence signals) and dark state (EIT in the transmitted probe signal and suppression in FWM and fluorescence signals) can be realized by controlling phase difference between the two circularly polarized components of a single coherent field9. In addition, the switch can also be obtained by manipulating the dressing field power and the probe detuning8,10,11,12.
In this paper, we experimentally demonstrate the phase-modulated switch between enhancement and suppression of SWM and fluorescence signals for the first time. First, the phase modulated switch between bright and dark states is realized under self-dressing condition. Second, we study the phase modulated switch under multi-dressing condition including the external-dressing. At last, we observe the dependence of the measured signals on relative phase.
Results
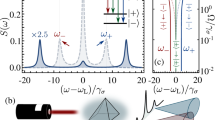
Our experiment is carried out in a 85Rb vapor cell. The energy levels 5S1/2(F = 3), 5S1/2(F = 2), 5P3/2, 5D3/2 and 5D5/2 constitute a five-level atomic system(Fig. 1(a)). The transition 5S1/2(F = 3) (|0〉) − 5P3/2 (|1〉) is probed by the laser beam E1 (frequency ω1, wave vector k1 and Rabi frequency G1). The transition 5P3/2 − 5S1/2(F = 2) (|3〉) is driven by two coupling beams E3 (ω3, k3 and G3) and  (ω3,
(ω3,  and
and  ). Two dressing beams E2 (ω2, k2 and G2) and E4 (ω4, k4 and G4) respectively drive the upper transitions 5P3/2 − 5D5/2 (|2〉) and 5P3/2 − 5D3/2 (|4〉). In normal experiment, the five beams are placed in a square-box pattern (Fig. 1(b)). The beams E2, E4, E3 and
). Two dressing beams E2 (ω2, k2 and G2) and E4 (ω4, k4 and G4) respectively drive the upper transitions 5P3/2 − 5D5/2 (|2〉) and 5P3/2 − 5D3/2 (|4〉). In normal experiment, the five beams are placed in a square-box pattern (Fig. 1(b)). The beams E2, E4, E3 and  propagate through the cell in the same direction with tiny angles about 0.3° between any two. In the opposite direction of E2 there is the probe beam E1. However, in our experiment, the normal experimental configuration should be modified since we study the phase-controlled switch. The coupling beam E2 (E4) is deviated with an angle α (β) from the normal position (Fig. 1(c) and 1(d)). In the experimental system, we use ES1 and ES2 to represent the SWM signals generated by E1, E3,
propagate through the cell in the same direction with tiny angles about 0.3° between any two. In the opposite direction of E2 there is the probe beam E1. However, in our experiment, the normal experimental configuration should be modified since we study the phase-controlled switch. The coupling beam E2 (E4) is deviated with an angle α (β) from the normal position (Fig. 1(c) and 1(d)). In the experimental system, we use ES1 and ES2 to represent the SWM signals generated by E1, E3,  and E2 and by E1, E3,
and E2 and by E1, E3,  and E4, respectively. Besides, the single-photon fluorescence caused by the photon decay from the level |1〉 is called R0. The sign R1 (R2) denotes the fluorescence due to the photon decay from the level |2〉 (|4〉).
and E4, respectively. Besides, the single-photon fluorescence caused by the photon decay from the level |1〉 is called R0. The sign R1 (R2) denotes the fluorescence due to the photon decay from the level |2〉 (|4〉).
Generally, we can obtain the density matrix elements  (related with EIT),
(related with EIT),  (related with SWM signal) and
(related with SWM signal) and  ,
,  ,
,  and
and  (related with fluorescence R0, R1 and R2) by solving the density-matrix equations. With Liouville pathway
(related with fluorescence R0, R1 and R2) by solving the density-matrix equations. With Liouville pathway  and E4 blocked, we can obtain
and E4 blocked, we can obtain

where d1 = iΔ1 + Γ10, d2 = i(Δ1 + Δ2) + Γ20, Δi = Ωi − ωi (Ωi denotes the level resonance frequency and Γij denotes the transverse relaxation rate between states |i〉 and |j〉). Significantly, the phase factor  (ΔΦ1 is related with the orientations of induced dipole moments μ1 and μ212) has been introduced into the dressing term |G2|2/d2 in
(ΔΦ1 is related with the orientations of induced dipole moments μ1 and μ212) has been introduced into the dressing term |G2|2/d2 in  since the angle α between E2 and the opposite direction of E1 is considered. With all five beams including E4 turned on,
since the angle α between E2 and the opposite direction of E1 is considered. With all five beams including E4 turned on,  is modified as
is modified as

with d4 = i(Δ1 + Δ4) + Γ40, where ΔΦ2 is the phase factor related with the angle β. Via the Liouville pathway  , the SWM signal ES1 can be obtained as
, the SWM signal ES1 can be obtained as

with E4 blocked or

with all five beams turned on, where  , d3 = i(Δ1 − Δ3) + Γ30, d5 = Γ21 + iΔ2 + |G3|2/[Γ23 + i(Δ2 + Δ3)] and
, d3 = i(Δ1 − Δ3) + Γ30, d5 = Γ21 + iΔ2 + |G3|2/[Γ23 + i(Δ2 + Δ3)] and  . Similarly, the SWM ES2 can be described by
. Similarly, the SWM ES2 can be described by

with  and d7 = Γ41 + iΔ4 + |G3|2/[Γ43 + i(Δ4 + Δ3)] and
and d7 = Γ41 + iΔ4 + |G3|2/[Γ43 + i(Δ4 + Δ3)] and

with  under self-dressing (the self-dressing effect refer to that one of the participating fields for generating SWM signals dresses the involved energy levels, which then modifies the SWM process itself, for example, the term
under self-dressing (the self-dressing effect refer to that one of the participating fields for generating SWM signals dresses the involved energy levels, which then modifies the SWM process itself, for example, the term  is the self-dressing term) and external dressing (the external-dressing effect refer to that the field will dresses the involved energy levels to modify the signals, while it is not the participated field for the generation of these signals, for example, the term
is the self-dressing term) and external dressing (the external-dressing effect refer to that the field will dresses the involved energy levels to modify the signals, while it is not the participated field for the generation of these signals, for example, the term  is the external dressing term) condition, respectively. For the fluorescence signals, via the Liouville pathway
is the external dressing term) condition, respectively. For the fluorescence signals, via the Liouville pathway  , one can obtain
, one can obtain

or

to describe the profile of fluorescence R0 under single-dressing or double-dressing case, respectively. With the pathway  , one can acquire
, one can acquire

to describe the DC background of R0. Consequently, the fluorescence R0 is proportional to  . For two-photon fluorescence R1, via
. For two-photon fluorescence R1, via  , we have
, we have

with d9 = Γ21 + iΔ2. Similarly, the other two-photon fluorescence R2 is described as

with d10 = Γ41 + iΔ4.
First, we consider the phase-modulated switch of self-dressed signals as shown in Fig. 2. In the experiment, we turn on E1, E2,  , E3 and block E4 and the signals are obtained by scanning Δ2 at different discrete designated Δ1 with ΔΦ1 = 0 (Fig. 2(a), viewed as the reference point at the normal configuration), ΔΦ1 = −π/5 (Fig. 2(b)) and ΔΦ1 = 3π/5 (Fig. 2(c)). In Fig. 2(a1), the EIT caused by E2, meeting Δ1 + Δ2 = 0, emerges in the larger range of the probe detuning. The EIA, satisfying Δ1 + Δ2 = |G2|2/Δ1, only appears at the large probe detuning, such as Δ1 = ±400 MHz. In Fig. 2(b1), we can find the probe transmission signals present as EIT at negative detunings Δ1 while change from strong EIT to partial-EIT-partial-EIA and lastly to week EIA with Δ1 increasing at positive detunings Δ1. In Fig. 2(c1), with the probe detuning transformed from negative to positive, the signals turn from EIA to partial-EIT-partial-EIA and lastly to EIT. Obviously, the variations of the probe transmission signals are quite the contrary in above three figures. This is caused by the modulation of the relative phase ΔΦ1 in the dressing term
, E3 and block E4 and the signals are obtained by scanning Δ2 at different discrete designated Δ1 with ΔΦ1 = 0 (Fig. 2(a), viewed as the reference point at the normal configuration), ΔΦ1 = −π/5 (Fig. 2(b)) and ΔΦ1 = 3π/5 (Fig. 2(c)). In Fig. 2(a1), the EIT caused by E2, meeting Δ1 + Δ2 = 0, emerges in the larger range of the probe detuning. The EIA, satisfying Δ1 + Δ2 = |G2|2/Δ1, only appears at the large probe detuning, such as Δ1 = ±400 MHz. In Fig. 2(b1), we can find the probe transmission signals present as EIT at negative detunings Δ1 while change from strong EIT to partial-EIT-partial-EIA and lastly to week EIA with Δ1 increasing at positive detunings Δ1. In Fig. 2(c1), with the probe detuning transformed from negative to positive, the signals turn from EIA to partial-EIT-partial-EIA and lastly to EIT. Obviously, the variations of the probe transmission signals are quite the contrary in above three figures. This is caused by the modulation of the relative phase ΔΦ1 in the dressing term  in
in  . Thus, at a certain detuning Δ1, we can switch EIT and EIA by adjusting the relative phase ΔΦ1. Similarly, the dressing effect on the SWM signal caused by
. Thus, at a certain detuning Δ1, we can switch EIT and EIA by adjusting the relative phase ΔΦ1. Similarly, the dressing effect on the SWM signal caused by  is also regulated by ΔΦ1. According to
is also regulated by ΔΦ1. According to  , the intensity of SWM has inverse correlation with cos(ΔΦ1 − θ) where θ = arctan(Δ1/Γ10). In the SWM signals, with the relative phase ΔΦ1 changed from 0 (Fig. 2(a2)) to −π/5 (Fig. 2(b2)), the intensity of SWM is obviously enhanced at Δ1 ≥ 0 since cos(−π/5 − θ) < cos(0 − θ) in the region while is suppressed at Δ1 < 0 for cos(−π/5 − θ) > cos(0 − θ) here. One can also see the difference between the SWM signals with ΔΦ1 = 0 (Fig. 2(a2)) and those with ΔΦ1 = 3π/5 (Fig. 2(c2)). Compared with the SWM in Fig. 2(a2), the SWM signal in Fig. 2(c2) is suppressed in the region Δ1 ≥ 200 MHz and enhanced in the region Δ1 < 200 MHz. From Fig. 2(a3) to Fig. 2(b3), one can find, with EIT converted to EIA (for example, at Δ1 = 200 MHz from Fig. 2(a1) to Fig. 2(b1)), on one hand, the dip of the corresponding fluorescence gets shallow due to the weakened dressing effect of E2 on R0 (in company with EIA) according to
, the intensity of SWM has inverse correlation with cos(ΔΦ1 − θ) where θ = arctan(Δ1/Γ10). In the SWM signals, with the relative phase ΔΦ1 changed from 0 (Fig. 2(a2)) to −π/5 (Fig. 2(b2)), the intensity of SWM is obviously enhanced at Δ1 ≥ 0 since cos(−π/5 − θ) < cos(0 − θ) in the region while is suppressed at Δ1 < 0 for cos(−π/5 − θ) > cos(0 − θ) here. One can also see the difference between the SWM signals with ΔΦ1 = 0 (Fig. 2(a2)) and those with ΔΦ1 = 3π/5 (Fig. 2(c2)). Compared with the SWM in Fig. 2(a2), the SWM signal in Fig. 2(c2) is suppressed in the region Δ1 ≥ 200 MHz and enhanced in the region Δ1 < 200 MHz. From Fig. 2(a3) to Fig. 2(b3), one can find, with EIT converted to EIA (for example, at Δ1 = 200 MHz from Fig. 2(a1) to Fig. 2(b1)), on one hand, the dip of the corresponding fluorescence gets shallow due to the weakened dressing effect of E2 on R0 (in company with EIA) according to  , on the other hand, the peaks in the dips get high because the original suppression (in company with EIT) induced by the dressing term
, on the other hand, the peaks in the dips get high because the original suppression (in company with EIT) induced by the dressing term  in
in  turns to enhancement (in company with EIA). While EIA (Fig. 2(a1)) is converted to EIT (Fig. 2(b1)), for example, at Δ1 = −400 MHz, the variations of the fluorescence signals are just the opposite. Same as above, when ΔΦ1 is changed from 0 (Fig. 2(a3)) to 3π/5 (Fig. 2(c3)), the similar variations also appear in the fluorescence signals, for example, at Δ1 = −200 MHz and Δ1 = 400 MHz. We have simulated the EIA-EIT switch in the probe transmission signal and suppression-enhancement transformation in SWM and fluorescence process, as shown in Fig. 2(d) which agrees with the experimental results very well.
turns to enhancement (in company with EIA). While EIA (Fig. 2(a1)) is converted to EIT (Fig. 2(b1)), for example, at Δ1 = −400 MHz, the variations of the fluorescence signals are just the opposite. Same as above, when ΔΦ1 is changed from 0 (Fig. 2(a3)) to 3π/5 (Fig. 2(c3)), the similar variations also appear in the fluorescence signals, for example, at Δ1 = −200 MHz and Δ1 = 400 MHz. We have simulated the EIA-EIT switch in the probe transmission signal and suppression-enhancement transformation in SWM and fluorescence process, as shown in Fig. 2(d) which agrees with the experimental results very well.
In each sub-curve, measured probe transmission signals ((a1), (b1) and (c1)), SWM signals ((a2), (b2) and (c2)) and fluorescence signals ((a3), (b3) and (c3)) versus Δ2 (Δ2 is scanned around −Δ1 from −90 MHz to 90 MHz) with E4 blocked.
Each sub-curve corresponds to different fixed Δ1. For (a1)–(a3) ΔΦ1 = 0, for (b1)–(b3) ΔΦ1 = −π/5 and for (c1)–(c3) ΔΦ1 = 3π/5. The other parameters are Δ3 = 0, G1 = 10.85 MHz, G2 = 19.46 MHz, G3 = 16.66 MHz and  . (d) Theoretical calculations for probe, SWM and fluorescence signals versus ΔΦ1 by scanning Δ2 at three typical detunings Δ1.
. (d) Theoretical calculations for probe, SWM and fluorescence signals versus ΔΦ1 by scanning Δ2 at three typical detunings Δ1.
Further, we turn on all five laser beams including E4 and observe the phase controlled switch of the multi-dressed (the multi-dressing effect is the case where two or more fields including self- and external-dressing fields dress the energy levels to modify the signals) signals by scanning Δ4 at different discrete fixed Δ1 (Fig. 3). In Fig. 3(a1), the peak higher than the baseline in each sub-curve represents the EIT induced by E4. The global profile formed from all baselines means the EIT induced by E2, meeting the condition Δ1 + Δ2 = 0. When we change the related phase ΔΦ2 from 0 (Fig. 3(a1)) to π/2 (Fig. 3(a2)), the original EITs are mostly switched to EIA. In Fig. 3(b1), the dip in each sub-curve shows the suppression on R0 caused by the dressing field E4 and the peak in each dip represents the two-photon fluorescence R2. The profile dip consisting of baselines reveals R0 suppressed by E2 owing to the dressing term |G2|2/d2 in  and the profile peak represents the two-photon fluorescence R1. With ΔΦ2 changed from 0 (Fig. 3(b1)) to π/2 (Fig. 3(b2)), the height of the peak in each sub-curve gets much high because the dressing term
and the profile peak represents the two-photon fluorescence R1. With ΔΦ2 changed from 0 (Fig. 3(b1)) to π/2 (Fig. 3(b2)), the height of the peak in each sub-curve gets much high because the dressing term  in
in  has generated the enhancement effect on R2 at ΔΦ2 = π/2. In this process, the dip in each sub-curve becomes shallow due to the weakened dressing effect of E4 on R0 caused by the modulation of ΔΦ2.
has generated the enhancement effect on R2 at ΔΦ2 = π/2. In this process, the dip in each sub-curve becomes shallow due to the weakened dressing effect of E4 on R0 caused by the modulation of ΔΦ2.
In each sub-curve, measured probe transmission signals (a), fluorescence signals (b) and SWM signals (c)–(d) versus Δ4 (Δ4 is scanned around −Δ1 from −90 MHz to 90 MHz) with the fixed Δ2.
Each sub-curve corresponds to different discrete fixed Δ1. (a1), (b1) and (c) Signals obtained with ΔΦ2 = 0. (a2), (b2) and (d) Signals obtained with ΔΦ2 = π/2. (a), (b), (c1) and (d1) Signals obtained with all beams turned on. (c2) and (d2) Signals obtained with E2 blocked. (c3) Signals obtained by subtracting the signals in (c2) from the signals in (c1). (d3) Signals obtained by subtracting the signals in (d2) from the signals in (d1). Other parameters are Δ2 = 100 MHz, Δ3 = 0, ΔΦ1 = 0, G1 = 10.72 MHz, G2 = 21.16 MHz, G3 = 18.87 MHz,  and G4 = 14.16 MHz.
and G4 = 14.16 MHz.
In Fig. 3(c1), the global profile (dashed curve) consisting of all baselines reveals the SWM signal ES1. In the ES1 signal, one can find the AT splitting which is because the self-dressing term |G1|2/d5 acts on the two-photon term d2 in  . The sub-curve at any Δ1 means the compound signal which includes two components: ID1 and ID2. ID1 denotes the enhancement or suppression intensity of ES1 (arising from the external-dressing field E4 according to
. The sub-curve at any Δ1 means the compound signal which includes two components: ID1 and ID2. ID1 denotes the enhancement or suppression intensity of ES1 (arising from the external-dressing field E4 according to  ) and ID2 signifies the SWM ES2 intensity with the suppression of E2. Figure 3(c2) shows the SWM ES2 intensity without the suppression of E2 which is denoted by IS2. The signals in Fig. 3(c3) are obtained by subtracting the signals (IS2) in Fig. 3(c2) from the signals (ID1 + ID2) in Fig. 3(c1). Therefore, the signals in Fig. 3(c3) represent two dressing results at different Δ1: one is ID1, the other is ID2-IS2 which is the suppressed intensity caused by E2 with regard to the SWM ES2. When we alter the relative phase ΔΦ2, the experiment results similar to Fig. 3(c) are obtained, as shown in Fig. 3(d1)–3(d3). The modulation of signals caused by relative phase can be observed clearly, as shown in Fig. 3(c3) and Fig. 3(d3). For instance, with the relative phase switched from 0 to π/2, the original suppression signals (at Δ1 + Δ2 = −45, −30 and −15 MHz) transform into partial-suppression-partial-enhancement signals and the intensities of original partial-suppression-partial-enhancement signals (at Δ1 + Δ2 = 0, 15, 30, 45 and 60 MHz) are strengthened significantly in correspondence with the EIT-EIA switch in Fig. 3(a). It is worth mentioning that the dressing result of E2 is basically invariable since the relative phase ΔΦ2 is only related to the dressing effect of E4.
) and ID2 signifies the SWM ES2 intensity with the suppression of E2. Figure 3(c2) shows the SWM ES2 intensity without the suppression of E2 which is denoted by IS2. The signals in Fig. 3(c3) are obtained by subtracting the signals (IS2) in Fig. 3(c2) from the signals (ID1 + ID2) in Fig. 3(c1). Therefore, the signals in Fig. 3(c3) represent two dressing results at different Δ1: one is ID1, the other is ID2-IS2 which is the suppressed intensity caused by E2 with regard to the SWM ES2. When we alter the relative phase ΔΦ2, the experiment results similar to Fig. 3(c) are obtained, as shown in Fig. 3(d1)–3(d3). The modulation of signals caused by relative phase can be observed clearly, as shown in Fig. 3(c3) and Fig. 3(d3). For instance, with the relative phase switched from 0 to π/2, the original suppression signals (at Δ1 + Δ2 = −45, −30 and −15 MHz) transform into partial-suppression-partial-enhancement signals and the intensities of original partial-suppression-partial-enhancement signals (at Δ1 + Δ2 = 0, 15, 30, 45 and 60 MHz) are strengthened significantly in correspondence with the EIT-EIA switch in Fig. 3(a). It is worth mentioning that the dressing result of E2 is basically invariable since the relative phase ΔΦ2 is only related to the dressing effect of E4.
Discussion
In order to clearly compare the variations of signals with the relative phase, we discuss the relative phase dependence of the measured signals by scanning Δ4 at the fixed detuning Δ1 under the above mentioned two cases of self-dressing and multi-dressing effects. First, with E2 blocked (Fig. 4(a), the self-dressing case), EIT in Fig. 4(a1) can be switched to EIA along with the change of ΔΦ2 from bottom to top. During this process, the strongest EIT and EIA separately appear at ΔΦ2 = −π/6 and ΔΦ2 = 3π/4. Depending on whether ΔΦ2 is greater than or less than π/4, the transmitted probe signal behaves mainly EIA or EIT. In the phase matching range where ΔΦ2 is altered from −π/6 to π/2, compared with the signals at the reference phase ΔΦ2 = 0, the SWM signal ES2 (Fig. 4(a2)) and fluorescence signal R2 (peaks in Fig. 4(a3)) get large when ΔΦ2 > 0 and become small while ΔΦ2 < 0 due to the switch of the dressing effect of E4 induced by ΔΦ2. The largest intensities of the SWM and fluorescence signals appear at partial-EIT-partial-EIA (ΔΦ2 = π/4) and EIA (ΔΦ2 = π/2), respectively. Along with continuing to increase ΔΦ2 from π/2 to π or to decrease ΔΦ2 from −π/6 to −π/3, which correspond to increasing the deflection angle β under the abnormal configuration (Fig. 1(d)), the SWM and fluorescence signal intensities decrease. This results from the classical effect with the phase mismatching condition. For the sake of clarity, the relative phase dependence of the fluorescence peak R2 is also shown by dash line with circles in Fig. 4(a4). The fluorescence suppression dip (Fig. 4(a3)) induced by E4 evolves from shallow to deep, then to shallow, the variation of which with the relative phase is also illustrated by the solid line with squares in Fig. 4(a4). The fluorescence suppression dip reaches the deepest at the stronger EIT. Next, with all five beams on (Fig. 4(b), the multi-dressing case), the evolvement of probe transmission signal in Fig. 4(b1) is similar to that in Fig. 4(a1) except that the EIT peak in Fig. 4(b1) is weaker than the one in Fig. 4(a1) due to the strong cascade-dressing interaction between E2 and E4. The peaks higher than the baselines in Fig. 4(b2) show the variation of the intensity ID2 of SWM signal ES2 under the dressing effect of E2, the evolvement of which approximates to that of the SWM peaks in Fig. 4(a2). The dips lower than the baselines in Fig. 4(b2) illustrate the variation of the suppression signal intensity ID1 of SWM ES1. In the phase matching range, the suppression dips of SWM ES1 are relatively deep under the condition of EIT and become shallow in the case of EIA. The variations of fluorescence peak R2 and fluorescence suppression dip in Fig. 4(b3), the relative phase dependences of which are shown in Fig. 4(b4), accord with those in Fig. 4(a3) except that the peaks become slightly small and the dips get shallow because of the cascade-dressing interaction between E2 and E4.
The transmitted probe ((a1), (b1)), SWM ((a2), (b2)) and fluorescence ((a3), (b3)) versus Δ4 at different relative phase ΔΦ2 = −π/3, −π/6, 0, π/4, π/2, 3π/4 and π from the bottom to top.
(a1),(a2) and (a3) Signals obtained with E2 blocked. (b1),(b2) and (b3) Signals obtained with all beams turned on. (a4) and (b4) the relative phase dependences of the fluorescence peak (dash line with circles) and the fluorescence dip (solid line with squares) in (a3) and (b3), respectively. The other parameters are ΔΦ1 = 0, Δ1 = −120 MHz, Δ2 = 150 MHz, Δ3 = 0, G1 = 11.84 MHz, G3 = 18.34 MHz,  , G2 = 26.11 MHz and G4 = 18 MHz.
, G2 = 26.11 MHz and G4 = 18 MHz.
In summary, we study the phase modulated switch between suppression and enhancement of fluorescence and SWM. By manipulating the relative phase, the original suppression on SWM and fluorescence signals can be transformed into enhancement in company with the conversion from EIT to EIA in the transmitted probe. Such switch can be applied in optical communication and quantum information processing.
Methods
In our experiment, there are five laser beams generated by four external cavity diode lasers (ECDL) with linewidths of less than or equal to 1 MHz. The probe laser beam E1 is from an ECDL with wavelength of 780.245 nm and a horizontal polarization. The two coupling laser beams E3 and  with wavelength 780.235 nm and a vertical polarization are split from another ECDL. The dressing laser beam E2 (E4) with wavelength of 775.978 nm (776.157 nm) and a vertical polarization are from other two ECDLs. The atomic vapor cell temperature is set at 60°C, corresponding to the typical density of 2 × 1011 cm−3. In our five-level atomic system, there exist two ladder-type EIT windows, two SWM signals and three fluorescence signals under the normal experimental configuration (Fig. 1(b)). Specifically, one SWM signal ES1 is generated by E1, E3,
with wavelength 780.235 nm and a vertical polarization are split from another ECDL. The dressing laser beam E2 (E4) with wavelength of 775.978 nm (776.157 nm) and a vertical polarization are from other two ECDLs. The atomic vapor cell temperature is set at 60°C, corresponding to the typical density of 2 × 1011 cm−3. In our five-level atomic system, there exist two ladder-type EIT windows, two SWM signals and three fluorescence signals under the normal experimental configuration (Fig. 1(b)). Specifically, one SWM signal ES1 is generated by E1, E3,  and E2 in the |0〉 − |1〉 − |2〉 ladder-type EIT window, which satisfies the phase matching condition
and E2 in the |0〉 − |1〉 − |2〉 ladder-type EIT window, which satisfies the phase matching condition  and the other SWM signal ES1 is generated by E1, E3,
and the other SWM signal ES1 is generated by E1, E3,  and E4 in the |0〉 − |1〉 − |4〉 ladder-type EIT window, which satisfies the phase matching condition
and E4 in the |0〉 − |1〉 − |4〉 ladder-type EIT window, which satisfies the phase matching condition  . Besides, the single-photon fluorescence R0 is caused by the photon decay from the level |1〉. The two-photon fluorescence R1 and R2 are due to the photon decay from the level |2〉 and |4〉, respectively. When the coupling beam E2 (E4) is deviated with an angle α (β) from the normal position (Fig. 1(c) and 1(d)), the above EIT windows, SWM and fluorescence signals will switch between bright state (EIA in the transmitted probe signal and enhancement in SWM and fluorescence signals) and dark state (EIT in the transmitted probe signal and suppression in SWM and fluorescence signals).
. Besides, the single-photon fluorescence R0 is caused by the photon decay from the level |1〉. The two-photon fluorescence R1 and R2 are due to the photon decay from the level |2〉 and |4〉, respectively. When the coupling beam E2 (E4) is deviated with an angle α (β) from the normal position (Fig. 1(c) and 1(d)), the above EIT windows, SWM and fluorescence signals will switch between bright state (EIA in the transmitted probe signal and enhancement in SWM and fluorescence signals) and dark state (EIT in the transmitted probe signal and suppression in SWM and fluorescence signals).
References
Wielandy, S. & Gaeta, A. Investigation of electromagnetically induced transparency in the strong probe regime. Phys. Rev. A 58, 2500–2505 (1998).
Kash, M. et al. Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas. Phys. Rev. Lett. 82, 5229–5232 (1999).
Ham, B. S., Shahriar, M. S. & Hemmer, P. R. Enhanced nondegenerate four-wave mixing owing to electromagnetically induced transparency in a spectral hole-burning crystal. Opt. Lett. 22, 1138–1140 (1997).
Harris, S. E. Electromagnetically induced transparency. Phys, Today 50, 36–42 (1997).
Qi, J. et al. Autler-Townes splitting in molecular lithium: Prospects for all-optical alignment of nonpolar molecules. Phys. Rev. Lett. 83, 288–291 (1999).
Qi, J. & Lyyra, A. M. Electromagnetically induced transparency and dark fluorescence in a cascade three-level diatomic lithium system. Phys. Rev. A, 73, 043810 (2006).
Akulshin, A. M., Barreiro, S. & Lezama, A. Electromagnetically induced absorption and transparency due to resonant two-field excitation of quasidegenerate levels in Rb vapor. Phys. Rev. A 57, 2996–3002 (1998).
Li, N. et al. Observation of dressed odd-order multi-wave mixing in five-level atomic medium. Opt. Exp. 20, 1912–1929 (2012).
Khadka, U., Zhang, Y. P. & Xiao, M. Control of multitransparency windows via dark-state phase manipulation. Phys. Rev. A, 81, 023830 (2010).
Li, C. et al. Observation of enhancement and suppression in four-wave mixing processes. Appl. Phys. Lett. 95, 041103 (2009).
Wang, Z. et al. Switching enhancement and suppression of four-wave mixing via a dressing field. J. Mod. Opt. 58, 802–809 (2011).
Hahn, K. H., King, D. A. & Harris, S. E. Nonlinear generation of 104.8-nm radiation within an absorption window in zinc. Phys. Rev. Lett. 65, 2777–2779 (1990).
Acknowledgements
This work was supported by the 973 Program (2012CB921804), NSFC (61078002, 61078020, 11104214, 61108017, 11104216, 61205112), RFDP (20110201110006, 20110201120005, 20100201120031), FRFCU (2012jdhz05, 2011jdhz07, xjj2011083, xjj2011084, xjj2012080, xjj2013089) and CPSF (2012M521773).
Author information
Authors and Affiliations
Contributions
Z.G.W. and Y.P.Z. provided the idea and main contributions to the theoretical and experimental analysis of this work. P.Y., P.Y.L., D.Z., H.Q.H. and H.T. contributed to the presentation and execution of the work. All authors discussed the results and contributed to writing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Wang, Z., Ying, P., Li, P. et al. Switching suppression and enhancement of fluorescence and six-wave mixing by phase modulation. Sci Rep 3, 3417 (2013). https://doi.org/10.1038/srep03417
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03417
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.