Abstract
Pressure can tune material's electronic properties and control its quantum state, making some systems present disconnected superconducting region as observed in iron chalcogenides and heavy fermion CeCu2Si2. For CaC6 superconductor (Tc of 11.5 K), applying pressure first Tc increases and then suppresses and the superconductivity of this compound is eventually disappeared at about 18 GPa. Here, we report a theoretical finding of the re-emergence of superconductivity in heavily compressed CaC6. The predicted phase III (space group Pmmn) with formation of carbon nanofoam is found to be stable at wide pressure range with a Tc up to 14.7 K at 78 GPa. Diamond-like carbon structure is adhered to the phase IV (Cmcm) for compressed CaC6 after 126 GPa, which has bad metallic behavior, indicating again departure from superconductivity. Re-emerged superconductivity in compressed CaC6 paves a new way to design new-type superconductor by inserting metal into nanoporous host lattice.
Similar content being viewed by others
Introduction
The metal doped organic compounds, graphite and solids with π-electrons networks, covering intercalation of alkali metals into buckminsterfullerene solids, metal intercalated graphite intercalation compounds (GICs) and alkali-metal-doped hydrocarbon materials, have recently received much attention in unveiling the new physical properties1, in particular superconductivity. So far, the highest Tc achieved in this class of materials is 38 K in pressurized Cs3C602,3. In the case of GICs, superconductivity was first observed in KC8 with a transition temperature of 0.15 K4. When using calcium atoms to replace the potassium atoms, which brought up to Tc of 11.5 K5,6, making CaC6 considered to be a template for exploring physical properties and superconducting mechanism of GICs-based superconductors as well as improving Tc value. Pressure, as a powerful tool, is often used to elevate superconductors' Tc. Gauzzi et al concluded that a large linear increase of Tc, from the ambient pressure value 11.5 K up to 15.1 K at 7.5 GPa, followed by a sudden drop to 5 K at about 8 GPa due to a first-order structural phase transition7. Theoretically, pressured-induced structural phase transition is ascribed to softening phonon modes related to in-plane vibrations from Ca atom9,10. It has been found that R-3m phase with hexagonal ring transforms into layer orthorhombic Cmmm structure with five- and eight-membered rings at 18 GPa11. Further, the pressure dependence of Tc studied in ac susceptibility measurements indicated that following an initial increase at the rate +0.39(1) K/GPa, Tc drops abruptly from 15 K to 4 K at 10 GPa and no superconducting transition is observed above 2 K between 18 and 32 GPa8. The repressed superconductivity at about 32 GPa should be correlated to further structural modification, signaling the vicinity of new phase. So far, however, available structural information is scare, which partly hinders theoretical or experimental studies on highly compressed CaC6, since it is indispensable to discern stable structures so as to explore hidden physical property of CaC6 at higher pressure.
Results
In this study, ab initio evolutionary algorithm (EA, USPEX code)12,13,14, which has been used to successfully predict high pressure phases of well-known materials, from element solids15,16 to binary17,18 or ternary19 compounds, is chosen to address low enthalpy phases of compressed CaC6. Under compression, a novel high pressure phase with nanoporous characteristic, controlling a wide pressure range, presents superconducting feature with considerable Tc of 14.7 K at 78 GPa. The re-emergence of superconductivity has been observed in various systems. Applying magnetic field, Lévy et al.20 observed superconductivity in the ferromagnet URhGe. Yuan et al.21 observed two disconnected superconducting phases in the pressure-temperature phase diagram of partially germanium-substituted CeCu2Si2. Very recently, Sun et al.22 reported that an unexpected superconducting phase re-emerges in the superconducting iron chalcogenides above 11.5 GPa. Here, re-entrance of superconductivity in compressed CaC6 provides new example to discern peculiar physical behavior of material at extreme conditions.
Pressure induces phase transitions from hexagonal to orthorhombic structures. Three orthorhombic high pressure new phases were found. The enthalpies vs. pressure curves of stable structures are presented in Fig. 1 a). We checked stability of CaC6 compared to its element solids using calcium's stable structures reported experimentally and theoretically23. No decomposition is observed in our calculations. The R-3m structure (referred as phase I) is the most stable structure below 19 GPa, followed by an orthorhombic C222 structure (referred as phase II, 19–39 GPa). The Pmmn phase (referred as phase III), a good metal (see supplementary Fig. S1), predominates in the pressure range of 39 to 126 GPa. Diamond-like carbon structure is adhered to the phase IV (Cmcm) for compressed CaC6 above 126 GPa, showing a bad metallic feature (see supplementary Fig. S2) due to existence of most of saturated sp3 hybridized carbons. Phase II with buckled five- or eight-membered ring's plane has very close enthalpy as of Cmmm structure with flat five- or eight-membered ring's plane reported by Csányi et al.11. For these two structures, we cannot say which structure is more stable than other in term of total energy due to their very small structural difference. As pressure increases, buckling characteristics in phase II gradually disappears, making it transform into Cmmm symmetry. Phonon spectrum calculations show that both C222 and Cmmm structures are dynamically stable. It is well known that non-hexagonal rings in a perfect graphene can be generated by introducing topological defects24,25. Here, external pressure and chemical pre-compression from calcium atoms provide the activation energy to drive di-vacancies defects formed, which leads to graphene layer in phase I transformed into octagonal and pentagonal carbon rings as observed in phase II.
(a) Relative enthalpy per chemical formula unit of compressed CaC6 as a function of pressure, referenced to the Pmmn structure. (b) Structural phase transitional diagram under cold pressure. (c) Atomic arrangement of the R-3m, C222, Pmmn and Cmcm structures of CaC6. The large ball represents the Ca atom. There are one, two, four and three in equivalent carbon atoms in the R-3m, C222, Pmmn and Cmcm structures, respectively. Under pressure, six-membered ring re-arranges into five- and eight-rings. Further, carbon polymerizes into three dimensional networks. Carbon mixing hybridization of sp3 + sp2 is observed in Pmmn and Cmcm phases. For Pmmn structure, sp2 hybridized bonds are linked by sp3 bonds, forming nanoporous structure, which is centered by calcium atoms chains. For Cmcm structure, the arrangement of carbon atoms is transformed into sp3 framework structure (diamond-like behavior) with sp2 bonds as borders and calcium ions have rearranged into 2D buckled plane.
In phase III, there are four types of in-equivalent carbon atoms in the unit cell (referred as C1, C2, C3 and C4, see supplementary Table S1), constructing carbon nanoporous structure. Along y-axis direction, carbon atoms form near quadrangular microporous, in which the size of porous lies in below 2 nm (about 0.61 nm and 0.59 nm at 0 GPa and 39 GPa, respectively). C1 and C2 (four carbon atoms in unit cell) show sp3 hybridization, other two types of carbons C3 and C4 form zigzag chains in the middle of border with two different bonding lengths (1.426 and 1.467 Å at 39 GPa, respectively, see supplementary Table S2), showing mostly sp2 hybridization. Ca atoms stay at center of porous (coordination number 8, with C3 and C4 atoms), forming 1D atomic chain along y-axis direction. At phase transition pressure (39 GPa), the nearest neighbor distance between C and Ca atoms is about 2.31 Å, which is slightly smaller than the value 2.489 Å of Ca-Ca bonding length (i.e., lattice parameter b), so there is stronger interaction between sp2 hybridized carbon and calcium because of charge accumulation in the bond region (see supplementary Fig. S3). Strong covalent bonding between carbon atoms (sp3 and sp2 hybridization) bring about its high rigidity, thus having high hardness. To explore its rigidity, we calculate elastic constants (see Table 1) and phonon spectrum of Pmmn structure at zero pressure. No imaginary frequency (see supplementary Fig. S4) was observed together with elastic stability in conjuncture with elastic and dynamical stability of carbon host lattice (space group Cmcm) at zero pressure (see Table 1 and see supplementary Fig. S5), signaling its rigidity. We also observed a meta-stable high pressure phase (P21/m) for compressed CaC6, in which carbon nanoporous structure includes armchair-type sp2 carbon chains in the middle of border in porous. For phase IV, under external pressure and chemical pre-compression from Ca sub-lattice, carbon atoms integrate closely into diamond-type property's strip (a total of five layer carbon atoms), while Ca atoms is also rearranged as the bulked plane compared to centered sites of porous in phase III. In diamond-like strips, internal carbon atoms form distorted tetrahedrons with obvious sp3 hybridization (see supplementary Fig. S3), while surface carbon atoms mostly form sp2 hybridization in armchair arrangement way along z-axis direction. The alternate carbon 3D framework and metal layers have an AαBβ arrangement, where the A and B represent the metal layers and α and β the diamond-like strip layers. The formed covalent three dimensional quasi-layer network (Ca layer-diamond-like layer-Ca layer- diamond-like layer) in phase IV largely enhances its incompressibility and hardness in comparison with phase III. Using suggested formula by Šimůnek and Vackář26, the estimated hardness is 34 GPa for Pmmn CaC6 at zero pressure, 45 GPa for Pmmn CaC6 at 39 GPa and 91 GPa for Cmcm CaC6 at 126 GPa.
The atomic arrangements of competing structures are shown in Fig. 1 c). The nearest neighbor distance between carbon atoms is 1.444 Å for the R-3m phase at 0 GPa, 1.417 Å for the C222 phase at 19 GPa, 1.426 Å for the Pmmn phase at 39 GPa and 1.460 Å for Cmcm phase at 126 GPa, which are close to the atomic distances in graphite. Interestingly, we found that only small change is observed for these distances as pressure increase, indicating very stiff chemical bonding between carbon atoms. For phase III from zero pressure to 39 GPa, carbon-carbon length only decreases 3 ~ 4%. The stiffness of C-C bonds corresponds to high vibration frequencies in phonon dispersions (discussed later).
Carbon nanoporous structure is very important because of its potential applications in many fields, such as H2 absorption, nanodevices, supercapacitors and lithium ion batteries, as well as chemical and bio-sensors. Structurally, the carbon foam, a three-dimensional porous including both sp2 and sp3 hybridized atoms, can be thought of as assembled from graphene planes interconnected rigidly with one another at a specific angle, forming a linear chain of sp3 bonded atoms along the junction27. Previously, supposed hybrid carbon foam structures with a mixed sp2/sp3 bonding character28,29 have received much less attention for lack of direct experimental observation. Recently, Tománek suggested carbon foam may form under non-equilibrium conditions near gain boundaries of a carbon-saturated metal substrate30. Here, (2, 2) zigzag carbon foam observed in phase III of CaC6 points out new easy-realized way experimentally via powerful high pressure tool. Electronic structure calculation shows that (2, 2) zigzag carbon foam is a semiconductor with narrow band gap (~0.49 eV, see supplementary Fig. S6). In view of nanoporous scientific and technological importance, we in detail explore host lattice's structural behavior (carbon lattice in phase Pmmn) at zero pressure. Removing calcium from lattice, relaxed host carbon sublattice shows higher symmetry (parent group Cmcm), which attributes to C1 and C2 as well as C3 and C4's symmetric degeneracy. For Ca guest sublattice, it forms body-centered tetragonal lattice with Immm symmetry. When adding calcium atoms into host lattice, interaction between Ca and C leads to lattice's symmetry decrease. Most exciting is that carbon nanoporous structure relaxed remains stable mechanically and dynamically at zero pressure (see Table 1 and supplementary Fig. S5). At zero pressure, carbon foam equilibrium structural parameters are listed in supplementary Table S1. The densities, carbon-carbon bond lengths and carbon-carbon bond angles of carbon foam and phase III of CaC6 as well as experimental values of graphite and diamond are listed in supplementary Table S2. The foam contains two-thirds 3-fold coordinated carbon atoms, labeled sp2 and one-third 4-fold coordinated carbon atoms, labeled sp3. The mass density of the optimized foam structure, ρ = 2.589 g/cm3, lies in-between the experimental values for graphite and diamond (see supplementary Table S2), which is highest density among reported carbon foams so far. Our carbon foam has peculiar structural behavior. There are three types of covalent bonds, sp2-sp2, sp2-sp3 and sp3-sp3 and five types of bond angles, sp2-sp2-sp2, sp2-sp3-sp2, sp2-sp3-sp3, sp3-sp2-sp3 and sp3-sp3-sp3, as presented in Table supplementary S2, which leads to non-hexagonal cross-section at junction. From supplementary Table S2, it can be seen that sp2-sp2 bond length in carbon foam is shorter than that in graphite, again indicating its stronger rigidity, which differs from previous reported carbon foam27,29. The size of nanoporous is often measured by its border length. For (2, 2) zigzag carbon foam observed here, it has 3.925 Å of width of tube-wall. The pore diameters (diagonal lengths) of nanoporous are 5.935 Å and 5.408 Å. Further, nanoporous's size can be modified by change numbers of carbon six-membered rings of borders, which helps to tune specific surface area and band gap so as to facilitate requisite applications in purification and separation, adsorption and catalysis31. This shape modification of nanoporous has been observed in other compressed GICs KC8 and LiC6. Using Li as guest, we obtained (2, 2) nanoporous and triangular nanoporous and using K, two kinds of nanoporous discovered (see supplementary Fig. S7). We can expect that more nanoporous solids can be exposed by other metal guest (such as Sc, Ba, Cs and Yb et al). Structure decides property, so further studies remains desirable to uncover structural evolution behavior of GICs under compression. Also we found that some carbon nanoporous systems with peculiar shape observed here present negative linear compressibility31. To add calcium atoms into (2, 2) zigzag carbon foam brings about porous distortion due to strong hybridization between calcium d-electrons and sp2 hybridized carbon p-electrons (see supplementary Fig. S1). As is shown in supplementary Table S2, there are five bond lengths and nine bond angles for carbon atoms. Carbon-carbon bond is slightly increased in length because of calcium atomic insertion but presents strong rigidity.
The small density of states (DOS) value at Fermi level for phase II exactly explains disappearance of Tc of CaC6 at the pressure range from 18 to 32 GPa experimentally8. Phase III has high DOS value at Fermi level compared with that of phase I (see supplementary Fig. S8) stimulates our intense interest on its potential superconductivity, since the electronic DOS at the Fermi level sensitively controls Tc. Energy bands of phase III at 39 GPa were shown in Fig. 2 (a). There are four energy bands, labeled as 1, 2, 3 and 4, crossing the Fermi level along several high symmetry directions in BZ. The most interesting feature is the appearance of a small region (TY direction in BZ) of one two-fold degenerating flat band lying just at the Fermi level around the Y point. The occurrence of flat and steep slopes near the Fermi level, which is a favorable condition for enhancing Cooper pair formation, has been thought to be essential to superconductivity32,33. The calculated DOS shows that a strong hybridization between the Ca-d electrons and sp2 carbon-p electrons (C3 and C4-p electrons) appears in the valence band from −2.78 to 0 eV and in the conduction band from 0 to 4 eV. Electrons from sp3 carbon (C1 and C2)-p electrons construct sp3 chemical bonding, lying mostly valence band from −16 eV to −2.78 eV. Dominant contributions to the DOS near the Fermi level come from the Ca-d electrons and sp2 carbon-p electrons (C3 and C4), whereas the Ca-p, C1-p and C2-p electrons make minor contributions to the DOS at the Fermi level (see supplementary Figure S1). Figure 2 (b) shows the Fermi surface (FS) of the Pmmn structure at 39 GPa. The labeled numbers (1–4) correspond to the labeled energy bands shown in Fig. 2 (a). The FS consists of two electron-hole oblate tube with an ‘8’-like section along the S-Y direction (all four bands), two hole tubes (bands 3 and 4) near the S-X-U-R plane and two hole pockets (band 2, Γ-Z direction). Obvious near parallel pieces of the Fermi surface exists, which favors to enhance the electron-phonon coupling. Both the Fermi pockets and the obvious Fermi nesting create strong electron-phonon interactions in CaC6. By further analyzing the wave functions of the four bands at the high symmetry points, we conclude that electron-like Fermi surfaces arise mainly from the Ca-dz2 and Ca-dx2 states, whereas hole-like Fermi surfaces attributes to the px and pz states from C3 and C4.
Electronic band structure along high symmetry lines of the Brillouin zone (top) and the Fermi surface (bottom) of CaC6 in the Pmmn phase at 39 GPa.
The energy bands crossing the Fermi level are labelled as 1, 2, 3 and 4, respectively. The projected Ca-d and C3- and C4-p electron characters are denoted by red circle and blue square, respectively.
Discussion
Phonon dispersions and the partial phonon density of states (PPHDOS) of phase III are shown in Fig. 3. The flat bands observed along S-X-U-R direction may serve as evidence of its local two-dimensional feature. Many soften modes are observed along the Γ-Z-T-Y and Γ-R directions (see also supplementary Fig. S9). As seen in the PPHDOS (in the right panel of Fig. 3), the calcium atomic vibrations mostly contribute to the phonon dispersions below 385 cm−1. The sp3 carbon (C1 and C2) atomic vibrations mainly dominate narrow frequency range around 1200 cm−1. The phonon dispersions between 385 and 889 cm−1 as well as above 1226 cm−1 are mainly due to the contributions of the sp2 carbon (C3 and C4) atomic vibrations.
Using the phonon linewidth  , we can identify the contribution to the electron-phonon interaction parameter λ from each mode (λQv ) based on the relation
, we can identify the contribution to the electron-phonon interaction parameter λ from each mode (λQv ) based on the relation  . Here, N(0) is the density of states at Fermi surface. We notice that large values of λQv lie at the high symmetry points Γ, S, X, U and R. For instance, we found that at the R point, λ(ω) originates mainly from contributions of the vibration modes at the frequency ranges of 242 to 305 cm−1. The calculated spectral function α2F(ω) and integrated λ(ω) of Pmmn CaC6 at 39 GPa are plotted in Fig. 4 a). The vibrations below 385 cm−1 provide the major contribution to λ (about 0.45). The low-frequency phonons (below 385 cm−1), which mostly involve the Ca and sp2 carbon (C3 and C4) atoms yield 54.5% of the total λ value. The phonons between 385 and 889 cm−1 mainly from sp2 carbon atoms, contribute to 32.4% of total λ. These results indicate that the calcium and sp2 carbon atoms in the Pmmn structure dominate superconductivity in CaC6, due to the prominent contributions to the electron-phonon interaction. Phonons from the Ca and sp2 carbon atoms together with the electrons from the Ca-d and sp2 C-p states provide the strong electron-phonon coupling necessary for strong superconductivity in Pmmn CaC6.
. Here, N(0) is the density of states at Fermi surface. We notice that large values of λQv lie at the high symmetry points Γ, S, X, U and R. For instance, we found that at the R point, λ(ω) originates mainly from contributions of the vibration modes at the frequency ranges of 242 to 305 cm−1. The calculated spectral function α2F(ω) and integrated λ(ω) of Pmmn CaC6 at 39 GPa are plotted in Fig. 4 a). The vibrations below 385 cm−1 provide the major contribution to λ (about 0.45). The low-frequency phonons (below 385 cm−1), which mostly involve the Ca and sp2 carbon (C3 and C4) atoms yield 54.5% of the total λ value. The phonons between 385 and 889 cm−1 mainly from sp2 carbon atoms, contribute to 32.4% of total λ. These results indicate that the calcium and sp2 carbon atoms in the Pmmn structure dominate superconductivity in CaC6, due to the prominent contributions to the electron-phonon interaction. Phonons from the Ca and sp2 carbon atoms together with the electrons from the Ca-d and sp2 C-p states provide the strong electron-phonon coupling necessary for strong superconductivity in Pmmn CaC6.
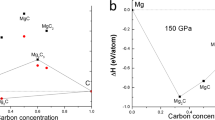
The Allen and Dynes modified formula34 was used to estimate the superconducting transition temperature Tc from the value of λ determined above. Taking a typical value of 0.115 for μ* along with the calculated ωlog of 642 cm−1, we obtained a Tc of 3.48 K for Pmmn CaC6 at 39 GPa. Applying pressure to Pmmn CaC6 clearly leads to λ first enhanced remarkably, then weaken and thus Tc corresponding responded (see supplementary Table S3). The calculated highest value of Tc is up to considerate 14.7 K (at 78 GPa). At 117 GPa, Tc is only 4.74 K. The calculated decrease of Tc agrees with occurrence of another new phase (Cmcm). The change of Tc with increasing pressure in CaC6 is summarized in Fig. 4 b). Phase III has consistent superconducting mechanism with phase I. Re-emerged superconductivity in CaC6 is closely related to structural transformation. Carbon nanofoam centered calcium atom chains in phase III brings about good metallic feature and strong electron-phonon coupling and thus superconductivity. Pressure-induced atomic hierarchical arrangement in phase IV, presenting diamond-like carbon strips (mostly sp3 carbon) and bucked calcium atomic layers, decreases its conductivity and thus represses superconductivity. By tuning electronic order (orbital or spin), pressure or magnetic field-driven the re-emergence of superconductivity has been observed in various systems including ferromagnet URhGe20, heavy fermion compound CeCu2Si221 and iron chalcogenides22.
To conclude, for compressed CaC6, carbon atom's arrangement is transformed from preceding two-dimensional (2D) layer into three-dimensional (3D) framework, while calcium ions themselves from 3D network turn into 2D buckled plane. A novel high pressure phase (Pmmn, two molecules/cell) with nanofoam carbon shows superconducting behavior due to enhanced electronic distribution at Fermi level as well as strong electron-phonon coupling, capturing critical superconducting temperature of 14.7 K at 78 GPa. The pressure-induced re-emergence of superconductivity in CaC6 signals a rich physics for graphite intercalation compounds under high compression. Although compressed LiC6 holds nanoporous carbon in its stable high pressure phases but it does not show the superconducting behavior. Therefore, further theoretical and experimental efforts are well worth to discern physical nature of GICs under compression.
Methods
Stable structures of GICs under cold compression were searched using evolutionary algorithm in combined with VASP code35 based on density functional theory within the generalised gradient approximation with the exchange-correlation functional of Perdew Burke Ernzerhof36, employing the projected augmented wave (PAW)37,38 method where 2s22p2 and 3s23p64s2 are treated as valence electrons for C and Ca atoms, respectively. For the crystal structure searches, we used a plane-wave basis set cutoff of 700 eV and performed the Brillouin zone integrations using a coarse k-point grid. The most interesting structures were further relaxed at a higher level of accuracy with a basis set cutoff of 1000 eV and a k-point grid of spacing 2π × 0.018 Å−1. Iterative relaxation of atomic positions was stopped when all forces were smaller than 0.001 eV/Å. The lattice dynamic and superconducting properties of Pmmn CaC6 were calculated by the Quantum ESPRESSO package39 using Vanderbilt-type ultra-soft potentials with cutoff energies of 55 Ry and 500 Ry for the wave functions and the charge density, respectively. The electronic Brillouin zone (BZ) integration in the phonon calculation was based on a 12 × 16 × 12 of Monkhorst-Pack k-point meshes. The dynamic matrix was computed based on a 2 × 4 × 2 mesh of phonon wave vectors. The electron-phonon coupling was convergent with a finer grid of 48 × 64 × 48 k of 0.01 Ry.
References
Rahnejat, K. C. et al. Charge density waves in the graphene sheets of the superconductor CaC6 . Nature Commun. 2, 558 (2011).
Ganin, A. Y. et al. Bulk superconductivity at 38 K in a molecular system. Nature Mater. 7, 367–371 (2008).
Takabayashi, Y. et al. The Disorder-Free Non-BCS Superconductor Cs3C60 Emerges from an Antiferromagnetic Insulator Parent State. Science 323, 1585–1590 (2009).
Hannay, N. B. et al. Superconductivity in Graphitic Compounds. Phys. Rev. Lett. 14, 225–226 (1965).
Emery, N. et al. Superconductivity of Bulk CaC6 . Phys. Rev. Lett. 95, 087003 (2005).
Weller, T. E., Ellerby, M., Saxena, S. S., Smith, R. P. & Skipper, N. T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nature Phys. 1, 39–41 (2005).
Gauzzi, A. et al. Enhancement of Superconductivity and Evidence of Structural Instability in Intercalated Graphite CaC6 under High Pressure. Phys. Rev. Lett. 98, 067002–067004 (2007).
Debessai, M. et al. Superconductivity for CaC6 to 32 GPa hydrostatic pressure. Phys. Rev. B 82, 132502 (2010).
Kim, J. S., Boeri, L., Kremer, R. K. & Razavi, F. S. Effect of pressure on superconducting Ca-intercalated graphite CaC6 . Phys. Rev. B 74, 214513 (2006).
Zhang, L. et al. Pressure-induced enhancement of electron-phonon coupling in superconducting CaC6 from first principles. Phys. Rev. B 74, 184519 (2006).
Csányi, G., Pickard, C. J., Simons, B. D. & Needs, R. J. Graphite intercalation compounds under pressure: A first-principles density functional theory study. Phys. Rev. B 75, 085432 (2007).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704–244715 (2006).
Glass, C. W., Oganov, A. R. & Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 175, 713–720 (2006).
Lyakhov, A. O., Oganov, A. R. & Valle, M. How to predict very large and complex crystal structures. Comput. Phys. Commun. 181, 1623–1632 (2010).
Oganov, A. R. et al. Ionic high-pressure form of elemental boron. Nature 457, 863–867 (2009).
Ma, Y. et al. Transparent dense sodium. Nature 458, 182–185 (2009).
Kolmogorov, A. N., Shah, S., Margine, E. R., Kleppe, A. K. & Jephcoat, A. P. Pressure-Driven Evolution of the Covalent Network in CaB6 . Phys. Rev. Lett. 109, 075501 (2012).
Li, Y. L. et al. Pressure-induced superconductivity in CaC2 . Proc Natl Acad Sci USA 110, 9289–9294 (2013).
Zhou, X.-F., Oganov, A. R., Qian, G.-R. & Zhu, Q. First-Principles Determination of the Structure of Magnesium Borohydride. Phys. Rev. Lett. 109, 245503 (2012).
Lévy, F., Sheikin, I., Grenier, B. & Huxley, A. D. Magnetic Field-Induced Superconductivity in the Ferromagnet URhGe. Science 309, 1343–1346 (2005).
Yuan, H. Q. et al. Observation of Two Distinct Superconducting Phases in CeCu2Si2. Science 302, 2104–2107 (2003).
Sun, L. et al. Re-emerging superconductivity at 48 kelvin in iron chalcogenides. Nature 483, 67–69 (2012).
Oganov, A. R. et al. Exotic behavior and crystal structures of calcium under pressure. Proc Natl Acad Sci USA 107, 7646–7651 (2010).
Kotakoski, J., Krasheninnikov, A. V., Kaiser, U. & Meyer, J. C. From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Phys. Rev. Lett. 106, 105505 (2011).
Lahiri, J., Lin, Y., Bozkurt, P., Oleynik, I. I. & Batzill, M. An extended defect in graphene as a metallic wire. Nature Nano. 5, 326–329 (2010).
Šimůnek, A. & Vackář, J. Hardness of Covalent and Ionic Crystals: First-Principle Calculations. Phys. Rev. Lett. 96, 085501 (2006).
Seifert, G., Kuc, A. & Heine, T. Hexagon preserving carbon nanofams. arXiv.org, 1106.5888 (2011).
Umemoto, K., Saito, S., Berber, S. & Tománek, D. Carbon foam: Spanning the phase space between graphite and diamond. Phys. Rev. B 64, 193409 (2001).
Zhao, Z. et al. Three Dimensional Carbon-Nanotube Polymers. ACS Nano 5, 7226–7234 (2011).
Zhu, Z. & Tománek, D. Formation and Stability of Cellular Carbon Foam Structures: An Ab Initio Study. Phys. Rev. Lett. 109, 135501 (2012).
Jiang, X., Zhao, J., Li, Y. L. & Ahuja, R. Tunable assembly of sp3 cross-linked three dimensional graphene monoliths: a first-principles prediction. Adv Func Mater. 10.1002/adfm.201301077 (2013).
Simon, A. Superconductivity and Chemistry. Angew. Chem., Int. Ed. Engl. 36, 1788–1806 (1997).
Tse, J. S., Yao, Y. & Tanaka, K. Novel Superconductivity in Metallic SnH4 under High Pressure. Phys. Rev. Lett. 98, 117004–117004 (2007).
Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905 (1975).
Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 29, 2044–2078 (2008).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Paolo, G. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys: condens. Mat. 21, 395502 (2009).
Acknowledgements
This work was supported by the NSFC (11047013), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and Jiangsu Overseas Research & Training Program for University Prominent Young & Middle-aged Teachers and Presidents. We thank Swedish Research Council (VR) for financial support. X.-J.C. was supported as part of EFree, an Energy Frontier Research Center funded by the Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award DESC0001057. Part of the calculations was performed at the Center for Computational Science of Hefei Institutes of Physical Science of Chinese Academy of Sciences, the ScGrid of Supercomputing Center and Computer Network Information Center of the Chinese Academy of Science and the Swedish National Infrastructure for Computing (SNIC).
Author information
Authors and Affiliations
Contributions
Y.-L.L. and R.A. designed research. Y.-L.L. performed research. Y.-L.L., R.A., W.L., X.J.C., Z.Z. and H.Q.L. analyzed data. Y.-L.L., X.J.C., H.Q.L. and R.A. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
CaC6-Suppl-Info
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Li, YL., Luo, W., Chen, XJ. et al. Formation of Nanofoam carbon and re-emergence of Superconductivity in compressed CaC6. Sci Rep 3, 3331 (2013). https://doi.org/10.1038/srep03331
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03331
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.