Abstract
The Leading Edge Vortex (LEV) is a universal mechanism enhancing lift in flying organisms. LEVs, generally illustrated as a single vortex attached to the wing throughout the downstroke, have not been studied quantitatively in freely flying insects. Previous findings are either qualitative or from flappers and tethered insects. We measure the flow above the wing of freely flying hawkmoths and find multiple simultaneous LEVs of varying strength and structure along the wingspan. At the inner wing there is a single, attached LEV, while at mid wing there are multiple LEVs and towards the wingtip flow separates. At mid wing the LEV circulation is ~40% higher than in the wake, implying that the circulation unrelated to the LEV may reduce lift. The strong and complex LEV suggests relatively high flight power in hawmoths. The variable LEV structure may result in variable force production, influencing flight control in the animals.
Similar content being viewed by others
Introduction
Insect flight has long been considered a paradox, defeating the expectations of steady state aerodynamics. We now know that the main lift enhancing mechanism that enables insects to generate enough lift to stay airborne is the Leading Edge Vortex, LEV1,2,3,4,5,6, which are also found in plant seeds7, birds8,9 and bats10. The LEV is generated by separation of the flow at the leading edge of the wing and enables the flow to reattach before the trailing edge. In flapping flight a single core LEV is generally found to stay attached to the top surface of the wing throughout the downstroke (e.g. ref. 11), although recent flapper studies and computational fluid dynamic (CFD) models have implicated a higher complexity with multiple cored vortices12,13,14,15,16. Earlier studies have sometimes described a transient LEV structure with the formation of a second LEV during the shedding of the first LEV16,17. However, this is different from the more recent studies, which indicate a multi-cored LEV that stays attached to the wing throughout the wingbeat12,13,15. The multi-cored LEV structure is proposed to be a potentially general feature of insect flight when a combination of flow conditions are met (see below), although the exact circumstances are still debated13,15. Although proposed as a general feature of insect flight, a multi-cored LEV has until now only been shown in accelerating butterflies18 and is yet to be demonstrated in steadily flying insects.
LEVs in insect flight have mainly been studied using flappers mimicking hawkmoths1,19,20 and other insects2,12,13,14,16,17,20 and more recently CFD models have also been used to study vortex dynamics (e.g. refs. 21,22,23 regarding hawkmoths). LEVs have also been demonstrated in live insects using smoke visualizations3,5,18,20 or Particle Image Velocimetry (PIV)4. Although some of the previous studies are based on freely flying animals3,5,18, a majority are based on tethered animals1,4,19,20,21,22,23 or in the case of flapper and CFD studies on simplified kinematics2,12,13,15. Tethering may affect the deformability of the thorax, which is responsible for the wing motion in insects such as moths24, or give exaggerated responses because the sensory feedback loop is disrupted25 and it is yet to be shown that tethering generates results similar to free flight (but see3). Furthermore, the body and its motions are generally ignored or difficult to simulate in flappers and computational models (but see26), as are wing mechanical properties, resulting in unrealistic aeroelastic interactions23. To the best of our knowledge, no data exist from live, freely flying, insects that quantify the flow structure of the LEV, to be used as a baseline for comparing the results from tethered animals, mechanical flappers and CFD-models. Here we perform detailed, high-resolution PIV, measurements of the flow above the wing of hummingbird hawkmoths (Macroglossum stellatarum) flying steadily in front of small feeders in a wind tunnel, at flight speeds (U∞) of 1 and 2 m/s to quantify the strength and structure of the LEV.
Results
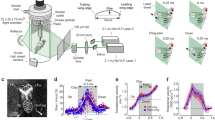
We find that the LEV structure is complex, with multiple vortices present simultaneously. The structure of the LEVs vary along the wingspan. On the inner wing there is generally a single, attached, LEV (Fig. 1a, Supplementary Figs. S4–5, Supplementary Table S2–3), at mid wing there are multiple LEVs (Fig. 1b, Fig. 2, Fig. 3, Supplementary Table S2–3). At the distal part of the wing the flow is fully separated (Fig. 1c), most likely representing a cut through the wing tip vortex, rolling up on the wing. At mid-wing multiple LEVs are clearly visible when constructing the streamlines of the flow above the wing and using swirl strength to identify separate vortex structures (Fig. 2).
Velocity fields (U∞ subtracted), showing every third vector and vorticity field, around the inner (a) (Moth 9), mid (b) (Moth 2) and distal (c) (Moth 2) part of a wing of a M. stellatarum flying at 2 m/s.
Flight direction is to the right. a and b are at mid downstroke and c at beginning of downstroke. Velocity is scaled according to the reference vector and vorticity according to the colorbar below the graphs. The velocity and vorticity fields are superimposed on the original images showing the wing profile as a gray area in the masked region (white). Cartoons to the right show the position of the laser along the span. The gray area shows the region where the structure and strength of the LEV changes along the wing length.
A zoomed in view of Fig. 1b showing the streamlines on top of the swirling strength (a measure of rotation) colorcoded according to the colorbar below.
Free-stream flow not subtracted. The swirling strength indicates two distinct LEVs separated by areas of zero swirl.
Velocity and vorticity plots of the LEV structure at mid wing at mid downstroke at three additional wingbeats from the same flight sequence as Fig. 1b of Moth 2 showing the diversity of the flow structure.
(a–c) show every second vector (free stream subtracted), scaled according to the vector below, on top of the vorticity, scaled according to the upper scale of the colorbar below the figure. (d–f) show the velocity, including the free stream flow, on top of the swirl strength scaled according to the lower scale of the colorbar below (zero swirl). Data from additional individuals and from further inwards on the wing are available in the Supplementary Figs. S1–S6.
In order to better understand the flow conditions governing the LEV stability we determine a number of relevant parameters. During the downstroke the mean angle of attack (α), the angle between the wing chord line and the oncoming airflow, is higher at the lower speed 41.6 ± 2.6°, mean ± S.E.M., (U∞ = 1 m/s) than at the higher speed, 32.2 ± 2.4° (U∞ = 2 m/s). Amplitude normalized by mean chord27,  , is 0.68 ± 0.03 at U∞ = 1 m/s and 0.81 ± 0.03 at U∞ = 2 m/s and wavelength normalized by
, is 0.68 ± 0.03 at U∞ = 1 m/s and 0.81 ± 0.03 at U∞ = 2 m/s and wavelength normalized by  27 is 1.6 ± 0.04 at U∞ = 1 m/s and 3.3 ± 0.12 at U∞ = 2 m/s. Reynolds number10 (Re), a measure of the ratio of inertial and viscous forces, based on mean speed at mid-wing during the downstroke and
27 is 1.6 ± 0.04 at U∞ = 1 m/s and 3.3 ± 0.12 at U∞ = 2 m/s. Reynolds number10 (Re), a measure of the ratio of inertial and viscous forces, based on mean speed at mid-wing during the downstroke and  is 1.0 103 (U∞ = 1 m/s) and 1.4 103 (U∞ = 2 m/s). The Reynolds number based on the wing tip velocity during mid downstroke and wing length (Res)15 is 5.7 103 (U∞ = 1 m/s) and 6.3 103 (U∞ = 2 m/s). The downstroke Strouhal number, Std, an index related to flow unsteadiness, calculated on the basis of the wing tip motion28 is 0.315 ± 0.018 at U∞ = 1 m/s and 0.316 ± 0.012 at U∞ = 2 m/s. Rossby number, Ro, a measure of the rotational acceleration initiating spanwise flow that mediate the growth of the LEV in flapping wings14, based on downstroke wingtip motion8, is 4.26 ± 0.17 at U∞ = 1 m/s and 4.21 ± 0.12 at U∞ = 2 m/s.
is 1.0 103 (U∞ = 1 m/s) and 1.4 103 (U∞ = 2 m/s). The Reynolds number based on the wing tip velocity during mid downstroke and wing length (Res)15 is 5.7 103 (U∞ = 1 m/s) and 6.3 103 (U∞ = 2 m/s). The downstroke Strouhal number, Std, an index related to flow unsteadiness, calculated on the basis of the wing tip motion28 is 0.315 ± 0.018 at U∞ = 1 m/s and 0.316 ± 0.012 at U∞ = 2 m/s. Rossby number, Ro, a measure of the rotational acceleration initiating spanwise flow that mediate the growth of the LEV in flapping wings14, based on downstroke wingtip motion8, is 4.26 ± 0.17 at U∞ = 1 m/s and 4.21 ± 0.12 at U∞ = 2 m/s.
In addition to determining the geometry of the vortex structure and the wing beat kinematics, we calculate the circulation (Γ) of the LEV (ΓLEV) and the circulation in the wake (ΓTEV) by integrating the vorticity above and behind the wing, respectively8,10. The ΓLEV, normalized by the local speed and chord, ΓLEV*, which is equal to half the local force coefficient, increases from inner to middle wing (Fig. 4), with a distinct increase at 33–47% of the wing length (Supplementary Fig. S6). The relative contribution of the LEV to lift production is determined by comparison with the circulation in the wake8,10. The ΓTEV* is more constant along the wing than the ΓLEV*. The LEV is stronger than the TEV at mid-wing, where ΓLEV is 132 ± 13% of the ΓTEV at U∞ = 1 m/s during mid downstroke and 145 ± 10% at U∞ = 2 m/s (Fig. 4). However, at the inner wing the LEV is weaker than the TEV during mid downstroke (39 ± 4% at U∞ = 1 m/s and 38 ± 16% at U∞ = 2 m/s), suggesting that the LEV contributes ~40% of the lift generated at the inner wing (Fig. 4). The transition zone shows intermediate values in ΓLEV* and ΓLEV/ΓTEV with a relatively high variation (Supplementary Fig. 6).
Circulation normalized by the local speed and chord of the LEV (closed) and TEV (open) along the length of the wing (0 at base, 1 at tip) at 1 m/s (a) and 2 m/s (c) flight speed.
ΓLEV/ΓTEV along the length of the wing at 1 m/s (b) and 2 m/s (d) flight speed. A ratio above one suggests that the LEV is stronger than the circulation found in the wake. The gray area indicates the location along the wing where we find an increase in ΓLEV and ΓLEV/ΓTEV. Values are means ± 2*SEM. Colors are beginning of downstroke (blue), mid downstroke (red) and end of downstroke (green).
Discussion
A double LEV structure, similar to the one found here, has also been described in delta wings (e.g. ref. 29), in recent flapper studies (e.g. refs. 12, 13), CFD models15 and in free-flying butterflies during accelerated flight18 (suggesting large forces). In addition, secondary vortex structures, considered shear layer instabilities, have been described as a rare phenomenon in both tethered and freely flying dragonflies3. Contrary to the results in butterflies, our results show that multiple, simultaneous, LEVs are the normal feature during steady flight in our freely flying hawkmoths, which is consistent with the recent flapper studies12,13 and CFD models15 that suggest the complex LEV to be a general feature of insect flight. Not only does the flow show multiple LEVs, but the flow structure also varies between measurements (Fig. 3, Supplementary Figs. S1–3), which to some degree is explained by kinematic variation. However, the variation is partly also due to spanwise variation in LEV stability14,15. Factors influencing the stability of LEVs in flapping flight is currently an active field of research2,8,12,13,14,15,23 and a few diagnostic measures for LEV stability have been identified. The combination of Re and α used by the hawkmoths are above the critical values (α > 30° and Re > 640) associated with the formation of multiple LEVs in a flapper13 and suggest the LEV may burst14,15. A bursting LEV is turbulent, but force augmentation is maintained. This agrees with our observed variation in the LEV structure and associated high force coefficient of the LEV at mid wing (Fig. 4). However, although the LEV may burst, it does not necessarily shed prematurely from the wing14,15. In fact, the downstroke Strouhal number, Std, is within the range associated with optimal vortex shedding30,31, i.e. vortices are shed at the start and end of the downstroke. The Ro is relatively high, indicating a potentially unstable LEV, but local Ro is lower towards the base of the wing, predicting a stable LEV-structure there. This is in general agreement with our findings. Although the on-wing LEV may indicate detachment from the wing surface during the downstroke (Fig. 3, Supplementary Figs. S1–3), images showing the entire wake of the downstroke do not display any clear signs of a shed LEV. This suggests that the LEVs contribute to the lift production until the end of the downstroke. Alternatively, the variation in the LEV structure may be caused by a chaotic interaction with the wake of the previous wingbeat as suggested by the combination of normalized amplitude and normalized wavelength27. However, if taking into account an inclined stroke plane, the wave length of the outer wing should be relatively higher than for the inner wing during the downstroke, reducing the relative risk of interactions at the outer wing. This is opposite to the higher variation at the outer wing than at the inner wing that we find here. The spanwise transition between the single LEV on the inner wing and the more complex structure at mid wing occurs at approximately a relative position 0.35–0.4 of the wing length from the root. This is close to the transition (~0.45) predicted by the Res of approximately 6 × 103 found here15. Although the prediction applies to hovering flight15 the close agreement with our results for forward flight calls for further studies of the factors determining LEV transition. Worth noting is that the transition point seems to coincide with the position of the wing tip of the hindwing. This may suggest a possible active control mechanism for the inner wing by the hind wing. Regardless of the cause of the variation in LEV structure the varying position of the LEV along the chord affects the pressure distribution6 and thus the pitching moments controlling wing twist and consequently the local angle of attack. These factors combine to a complex system affecting force generation that may influence flight control.
The increase in ΓLEV* is associated with the transition from a single to multiple LEVs, suggesting that the increased LEV complexity results in an increased local force coefficient of the LEV. The ΓLEV/ΓTEV above unity at the mid wing, where most of the lift is generated, suggests that the LEV is solely responsible for the lift generation at this part of the wing. In fact, the ΓLEV/ΓTEV significantly above unity suggests that the LEV not only complements the bound circulation, ΓB, but instead requires the bound circulation to reverse at mid wing, because according to Kelvin's circulation theorem, the net change in circulation in a closed system is zero32. This means that the circulation moving with the wing (ΓB + ΓLEV) should be equal, but of opposite spin, to the circulation shed into the wake (ΓTEV). Since the decay of circulation is negligible within the time frame of a downstroke33, the bound circulation of the wing (ΓB), which we cannot estimate directly, is required to be of opposite spin to ΓLEV. Our results thus show that the LEV is the main lift-generating mechanism in freely flying hummingbird hawkmoths and that the LEV is stronger than expected since a weaker LEV, where ΓB ≥ 0, may produce the same lift while adding less kinetic energy to the air.
Hovering specialist vertebrates, i.e. hummingbirds9, flycatchers8 and bats10, also use LEVs at low flight speeds. However, the LEVs in these animals have not displayed the complexity found here and the LEVs are closer to the wing surface despite the higher Re of bird and bat flight. Flexibility of the wings may stabilize the LEV8,23 and one explanation for the differences between insects and vertebrates may be a difference in mechanical properties of the wings34,35. Alternatively, the ability of active control of the wing during a wingbeat, in response to sensory information36, may be more likely to occur in vertebrates as a consequence of lower wingbeat frequency and ability to morph the wings. Our results thus indicate differences in flow control related to phylogenetic history, with the potential to impose limitations to animal flight performance.
Methods
Six moths (Macroglossum stellatarum), Table S1, were flying freely in front of a feeder at speeds (U∞) 1 and 2 m/s in a wind tunnel.
2D velocity fields were determined using PIV in a vertical plane, 37 × 37 mm2 parallel to U∞ [x, z] around the wing. Images of fog particles (~1 μm) were captured in the plane illuminated by a laser (Litron LPY732 series, 532 nm, 200 Hz). Images were captured (HighSpeedStar3; 1024 × 1024 pixels, Zeiss Makro-Planar T, 100 mm, filter 532 ± 5 nm) and analyzed using Davis 7.4 (LaVision, Germany) after calibration (plate type 22 and “self-calibration”). 127 frames were analysed (box size 12 × 12, 50% overlap) after masking the wing and shadow. After removing erroneous vectors, vector fields were smoothed once (3 × 3 box size).
Two synchronized cameras (500 Hz) filmed side- and top views for 3D kinematics28. Nine sequences (3–5 wing beats), all individuals contributed at least one sequence, at each speed were analysed. Mean speed at mid wing during the downstroke (Udm), wing beat frequency (f = 82.4 ± 1.3 Hz [mean ± S.E.M.] at U∞ = 1 m/s and 79.7 ± 2.2 Hz at U∞ = 2 m/s) and amplitude (θ = 72.3 ± 4.1° at U∞ = 1 m/s and 70.8 ± 5.4° at U∞ = 2 m/s), were determined.
The presences of multiple LEVs were confirmed by patches of positive swirling strength37 separated by zero swirl. Circulation (Γ) was determined for the LEV and for the vortices shed into the wake at the trailing edge, including the start vortex (TEV), by integrating spanwise vorticity (ωy) within an area of interest. The position of vector fields were determined from the laser position along the wing length, grouped into four groups (0–33%, 34–47%, 48–80% and 81–100%) and given a time stamp as beginning of downstroke (bd), mid downstroke (md) and end of downstroke (ed).
We estimated the wing speed ( ) along the wing length during each phase (bd, md, ed) by fitting a sine function with a period of 2*downstroke ratio to the wing speed during a normalized downstroke. The downstroke was subdivided into three equal periods and the mean speed of each period was calculated by integrating the sine function over the period and divide by the normalized time of the period. The chord distribution along the wing was measured from photos of the animals. For each combination of individual and phase we then calculated Uc for each measurement, based on the spanwise location, which was used to normalize the circulation. The normalized circulation is half the lift coefficient
) along the wing length during each phase (bd, md, ed) by fitting a sine function with a period of 2*downstroke ratio to the wing speed during a normalized downstroke. The downstroke was subdivided into three equal periods and the mean speed of each period was calculated by integrating the sine function over the period and divide by the normalized time of the period. The chord distribution along the wing was measured from photos of the animals. For each combination of individual and phase we then calculated Uc for each measurement, based on the spanwise location, which was used to normalize the circulation. The normalized circulation is half the lift coefficient  . We estimated means and SEM of the normalized circulation (
. We estimated means and SEM of the normalized circulation ( ) and
) and  as the intercept (equal to the mean of the individual means) and SEM in a mixed model in JMP (SAS Institute) with individual as a random variable.
as the intercept (equal to the mean of the individual means) and SEM in a mixed model in JMP (SAS Institute) with individual as a random variable.
References
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. Leading-edge vortices in insect flight. Nature 384, 626–630 (1996).
Birch, J. M., Dickson, W. B. & Dickinson, M. H. Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds number. J. Exp. Biol. 207, 1063–1072 (2004).
Thomas, A. L. R., Taylor, G. K., Srygley, R. B., Nudds, R. L. & Bomphrey, R. J. Dragonfly flight: free-flight and tethered flow visualizations reveal a diverse array of unsteady lift generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 207, 4299–4323 (2004).
Bomphrey, R. J., Lawson, N. J., Harding, N. J., Taylor, G. K. & Thomas, A. L. R. The aerodynamics of Manduca sexta: digital particle image velocimetry analysis of the leading-edge vortex. J. Exp. Biol. 208, 1079–1094 (2005).
Bomphrey, R. J., Taylor, G. K. & Thomas, A. L. R. Smoke visualization of free-flying bumblebees indicates independent leading-edge vortices on each wing pair. Exp. Fluids 46, 811–821 (2009).
Shyy, W. et al. Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerospace Sci. 46, 284–327 (2010).
Lentink, D., Dickson, W. B., van Leeuwen, J. L. & Dickinson, M. H. Leading-edge vortices elevate lift of autorotating plant seeds. Science 324, 1438–1440 (2009).
Muijres, F. T., Johansson, L. C. & Hedenström, A. Leading edge vortex in a slow-flying passerine. Biol. Lett. 8, 554–557 (2012).
Warrick, D. R., Tobalske, B. W. & Powers, D. R. Lift production in the hovering hummingbird. Proc. R. Soc. B 276, 3747–3752 (2009).
Muijres, F. T. et al. Leading-edge vortex improves lift in slow-flying bats. Science 319, 1250–1253 (2008).
Liu, H. & Aono, H. Size effects on insect hovering aerodynamics: an integrated computational study. Bioinsp. Biomim. 4, 1–13 (2009).
Lu, Y. & Shen, G. X. Three-dimensional flow structures and evolution of the leading-edge vortices on a flapping wing. J. Exp. Biol. 211, 1221–1230 (2008).
Lu, Y., Shen, G. X. & Lai, G. J. Dual leading-edge vortices on flapping wings. J. Exp. Biol. 209, 5005–5016 (2006).
Lentink, D. & Dickinson, M. H. Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Exp. Biol. 212, 2705–2719 (2009).
Harbig, R. R., Sheridan, J. & Thompson, M. C. Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192 (2013).
Ramasamy, M. & Leishman, J. G. Phase-locked particle image velocimetry measurements of a flapping wing. J. Aircraft 43, 1067–1875 (2006).
Maxworthy, T. Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight. Part 1. Dynamics of the “fling”. J. Fluid Mech. 93, 47–63 (1979).
Srygley, R. B. & Thomas, A. L. R. Unconventional lift-generating mechanisms in free flying butterflies. Nature 420, 660–664 (2002).
van den Berg, C. & Ellington, C. P. The three-dimensional leading-edge vortex of a ‘hovering’ model hawkmoth. Phil. Trans. R. Soc. Lond. B 352, 329–340 (1997).
Luttges, M. W. in Frontiers In Experimental Fluid Mechanics (ed Gad-el-Hak, M.) 429–456 (Springer, 1989).
Liu, H., Ellington, C. P., Kawachi, K., van den Berg, C. & Willmott, A. P. A computational fluid dynamic study of Hawkmoth hovering. J. Exp. Biol. 201, 461–477 (1998).
Aono, H., Shyy, W. & Liu, H. Near wake vortex dynamics of a hovering hawkmoth. Acta Mech. Sin. 25, 23–36 (2009).
Nakata, T. & Liu, H. Aerodynamic performance of a hovering hawkmoth with flexible wings: a computational approach. Proc. R. Soc. B 279, 722–731 (2012).
Dudley, R. The biomechanics of insect flight: form, function, evolution. 1st edn, (Princeton University Press, 2000).
Taylor, G. K. et al. New experimental approaches to the biology of flight control systems. J. Exp. Biol. 211, 258–266 (2008).
Gao, N., Aono, H. & Liu, H. Perturbation analysis of 6DoF flight dynamics and passive dynamic stability of hovering fruit fly Drosophila melanogaster. J. Theor. Biol. 270, 98–111 (2011).
Lentink, D., Van Heijst, G. F., Muijres, F. T. & Van Leeuwen, J. L. Vortex interactions with flapping wings and fins can be unpredictable. Biol. Lett. 6, 394–397 (2010).
Wolf, M., Johansson, L. C., von Busse, R., Winter, Y. & Hedenström, A. Kinematics of flight and the relationship to the vortex wake of a Pallas' long tongued bat (Glossophaga soricina). J. Exp. Biol. 213, 2142–2153 (2010).
Gordon, S. T. & Gursul, I. Buffeting Flows over a Low-Sweep Delta Wing. AIAA J. 42, 1737–1745 (2004).
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. Oscillating foils of high propulsive efficiency. J. Fluid. Mech. 360, 41–72 (1998).
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. Flying and swimming animals cruise at Strouhal number tuned for high power efficiency. Nature 425, 707–711 (2003).
Anderson, J. D. Fundamentals of aerodynamics. 4th edn, (McGraw-Hill, 2007).
Wang, X. X. & Wu, Z. N. Stroke-averaged lift forces due to vortex rings and their mutual interactions for a flapping flight model. J. Fluid Mech. 654, 453–472 (2010).
Swartz, S. M. & Middleton, K. M. Biomechanics of the Bat Limb Skeleton: Scaling, Material Properties and Mechanics. Cells Tissues Organs 187, 59–84 (2008).
Combes, S. A. & Daniel, T. L. Flexural stiffness in insect wings. I. Scaling and the influence of wing venation. J. Exp. Biol. 206, 2979–2987 (2003).
Sterbing-D'Angelo, S. et al. Bat wing sensors support flight control. PNAS 108, 11291–11296 (2011).
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396 (1999).
Acknowledgements
Research was funded by the Knut and Alice Wallenberg foundation to A.H., by the Royal Physiographic Society in Lund to L.C.J. and by the Swedish Research Council to L.C.J., A.H. and A.K. This report received support from the Centre for Animal Movement Research (CAnMove) financed by a Linnaeus grant (349-2007-8690) from the Swedish Research Council and Lund University.
Author information
Authors and Affiliations
Contributions
Experiments were planned and conducted by L.C.J., S.E., A.H. and A.K. Analysis was performed by L.C.J. and S.E. Interpretation of the results were done by L.C.J., M.K.H. and A.H. All authors contributed to the writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Johansson, L., Engel, S., Kelber, A. et al. Multiple leading edge vortices of unexpected strength in freely flying hawkmoth. Sci Rep 3, 3264 (2013). https://doi.org/10.1038/srep03264
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03264
This article is cited by
-
Investigate the Wake Flow on Houseflies with Particle-Tracking-Velocimetry and Schlieren Photography
Journal of Bionic Engineering (2023)
-
Scaling trends of bird’s alular feathers in connection to leading-edge vortex flow over hand-wing
Scientific Reports (2020)
-
Ear-body lift and a novel thrust generating mechanism revealed by the complex wake of brown long-eared bats (Plecotus auritus)
Scientific Reports (2016)
-
Vortices behavior depending on the aspect ratio of an insect-like flapping wing in hover
Experiments in Fluids (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.