Abstract
The utilization of spin waves as eigenmodes of the magnetization dynamics for information processing and communication has been widely explored recently due to its high operational speed with low power consumption and possible applications for quantum computations. Previous proposals of spin wave Mach-Zehnder devices were based on the spin wave phase, a delicate entity which can be easily disrupted. Here, we propose a complete logic system based on the spin wave amplitude utilizing the nonreciprocal spin wave behavior excited by microstrip antennas. The experimental data reveal that the nonreciprocity of magnetostatic surface spin wave can be tuned by the bias magnetic field. Furthermore, engineering of the device structure could result in a high nonreciprocity factor for spin wave logic applications.
Similar content being viewed by others
Introduction
Since the scaling of the conventional semiconductor devices approaches its physical and operational limit1, various schemes have been proposed to improve the performance of devices in terms of the computational capability and power dissipation including the utilization of photon2,3, phonon4 and spin of electrons5,6,7,8,9,10. Spintronics is an emerging technology which exploits the intrinsic spin of electrons and its associated magnetic moments, in addition to their fundamental electronic charges. Different spin based logic circuits have been proposed including magnetic cellular automata11,12, programmable magnetoresistive elements13, domain walls14,15,16, spin currents17,18 and spin wave19,20 based logic devices. Spin waves have a characteristic frequency in the gigahertz range21,22,23,24,25 with a large group velocity (~a few tens of μm/ns) and the capability to be guided along a ferromagnetic material allows it to be considered as a promising candidate for information processing26,27,28,29. The previous studies of the spin wave logic devices based on the phase of spin wave require a controlled phase shifter which complicates the device structure19,30,31 especially for submicron size devices where the lateral confinement forces the magnetic system to obtain more than one spin wave frequency with different phase velocities21. In addition, the spin wave phase is a continuous variable and delicate entity that could be easily disrupted by imperfections and magnetic inhomogeneities32 and is extremely sensitive to the dimensions of devices, which makes the spin wave logic devices to be less reliable and high bit error rates33.
In contrast to a widely used dielectric material, yttrium iron garnet (YIG) in the spin wave studies, metallic ferromagnetic materials are more compatible to the standard semiconductor technology and can be easily scaled down. Depending on the relative orientation between the external magnetic field and the spin wave propagation direction, the different modes of magnetostatic spin waves can exist. When the magnetic field is in the plane of the ferromagnetic film and normal to the wavevector of spin waves, the Damon-Eshbach (DE) surface spin wave propagates on the film surfaces34,35. It has been known that the surface mode has a nonreciprocal behavior in the spin wave amplitude for the spin waves with opposite signs of wavevectors (±k)34,35,36,37. In thin ferromagnetic films, the nonreciprocal behavior of magnetostatic surface spin waves is a consequence of the asymmetric distribution of the out-of-plane component of the excitation field (Supplementary Information S1)35,38.
Here we show that the nonreciprocity value of surface spin waves is not a constant, but it can be tuned by the external bias magnetic field. We further discuss how to engineer a larger nonreciprocity ratio. Utilizing the spin wave amplitude due to the nonreciprocal spin wave behavior, a new type of complete spin wave logic device is proposed.
Results
Nonreciprocal spin wave propagation
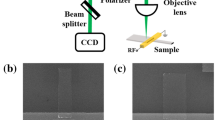
The schematic diagram of the device structure is shown in Fig. 1(a) consisting of a 20 nm thick Ni80Fe20 (permalloy) film isolated from the excitation and detection striplines (antennas) by an oxide layer. The bias magnetic field is applied in the y-direction and the propagating spin wave in the x-direction is detected using an inductive technique. The optical image and scanning electron micrograph (SEM) of the fabricated device are shown in Fig. 1(b, c), respectively, in which g = 5 μm is the gap distance between the excitation and detection stripline, W = 9 μm is the width of the ground line and S = 3 μm is the width of the signal line. Two different characterization methods have been performed such as frequency domain measurements using a sinusoidal microwave excitation and time domain measurements using a pulse inductive microwave magnetometer.
Device structure.
(a) Schematic illustration of the device structure. The device includes a 20 nm thick permalloy film separated from the striplines by 50 nm of SiO2. The striplines are in an asymmetric coplanar waveguide configuration made of Cr (5 nm)/Ag (150 nm)/Pt (5 nm) with a signal width (S) of 3 μm and ground width (W) of 9 μm. The bias magnetic field is applied in the y-direction and propagating spin wave in the x-direction is detected by the antenna using an inductive technique. (b) The optical microscope picture of a device. (c) Scanning electron micrograph (SEM) of a device.
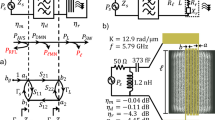
The frequency spectra of the propagating spin wave for magnetic fields of ±135, ±225 and ±300 Oe are shown in Fig. 2(a). One can see a clear nonreciprocity of the surface spin wave for positive and negative fields which is equivalent to the opposite signs of wavevectors (Supplementary Information S2). Furthermore, spin waves contain two major frequencies where the amplitude of the higher frequency peak is much smaller than that of the lower frequency one. The surface spin wave has a dispersion relation of  in which Ms is the saturation magnetization and γ0 is the gyromagnetic constant, d is the film thickness and k is the spin wave wavevector34. The spin wave spectrum that is measured for different magnetic fields is shown in Fig. 2(b). A clear quadratic-like behavior of the spin wave frequency versus magnetic field is consistent with the surface spin wave dispersion relationship. By fitting the main frequency of the experimental data in Fig. 2(b) with the spin wave dispersion relation, a wavevector of k ± Δk = 0.57 ± 0.33 μm−1 is obtained which is in line with the previous reports with inductive method characterization25,37. The observation of two frequencies for the spin wave at a bias magnetic field can be understood based on the presence of two different wavevectors. Δk is proportional to the inverse of the signal line width (S)25, therefore for a narrow stripline (3 μm), the different wavevectors are present, while only one frequency is present for a wide stripline (10 μm) (Supplementary Information S3). In Fig. 2(b) the lower branch corresponding to positive bias fields has larger amplitudes compared to the upper branch with negative bias fields, demonstrating the nonreciprocity of spin waves.
in which Ms is the saturation magnetization and γ0 is the gyromagnetic constant, d is the film thickness and k is the spin wave wavevector34. The spin wave spectrum that is measured for different magnetic fields is shown in Fig. 2(b). A clear quadratic-like behavior of the spin wave frequency versus magnetic field is consistent with the surface spin wave dispersion relationship. By fitting the main frequency of the experimental data in Fig. 2(b) with the spin wave dispersion relation, a wavevector of k ± Δk = 0.57 ± 0.33 μm−1 is obtained which is in line with the previous reports with inductive method characterization25,37. The observation of two frequencies for the spin wave at a bias magnetic field can be understood based on the presence of two different wavevectors. Δk is proportional to the inverse of the signal line width (S)25, therefore for a narrow stripline (3 μm), the different wavevectors are present, while only one frequency is present for a wide stripline (10 μm) (Supplementary Information S3). In Fig. 2(b) the lower branch corresponding to positive bias fields has larger amplitudes compared to the upper branch with negative bias fields, demonstrating the nonreciprocity of spin waves.
Nonreciprocal spin wave propagation in frequency domain.
(a) Spin wave excitation spectra measured using a vector network analyzer for different magnetic fields of ±135, ±225 and ±300 Oe. The data of the positive fields are shifted by 0.01 dBm for clarity. (b) Spin wave frequency measured at different magnetic fields. (c) Simulation results of the surface spin wave at different magnetic fields. (d) Nonreciprocity factors of surface spin wave measured at different magnetic fields in both frequency and time domains and the corresponding micromagnetic simulation results.
In order to better understand the nonreciprocity of spin waves, we have also performed micromagnetic simulations as can be seen in Fig. 2(c) (Supplementary Information S4). The simulation results are similar to the experimental results. In Fig. 2(d), we have calculated the spin wave nonreciprocity factor  in the frequency domain which is the ratio of the spin wave amplitude at opposite bias magnetic fields or at opposite wavevectors. The spin wave nonreciprocity is a function of the bias field and it increases upon increasing the bias magnetic field. The nonreciprocity factor is similar for an impulse and microwave sinusoidal excitations36,37 (Supplementary Information S5). The simulated nonreciprocity matches well with the experimental results as shown in Fig. 2(d).
in the frequency domain which is the ratio of the spin wave amplitude at opposite bias magnetic fields or at opposite wavevectors. The spin wave nonreciprocity is a function of the bias field and it increases upon increasing the bias magnetic field. The nonreciprocity factor is similar for an impulse and microwave sinusoidal excitations36,37 (Supplementary Information S5). The simulated nonreciprocity matches well with the experimental results as shown in Fig. 2(d).
Nonreciprocity of spin waves in time domain
We have also performed time-resolved measurements of spin wave dynamics in Fig. 3(a–c) for a magnetic field of ±60, ±135 and ±200 Oe, respectively. It is clear that the nonreciprocity of spin wave has increased by increasing the field from 60 to 200 Oe which is also consistent with the frequency domain data in Fig. 2(d). The micromagnetic simulation results in Fig. 3(d–f) also show an increase in the nonreciprocity by increasing the bias magnetic field similar to the experimental results in Fig. 3(a–c). Note that the detected spin wave voltage is associated to the change of the magnetization in time. The above experimental and simulation results show that the amplitude of spin-wave packet can be changed by inversing the magnetization direction or by inversing the propagation direction. Therefore, the nonreciprocity of the surface spin wave amplitude is a promising candidate for the implementation of spin wave logic circuits.
Time domain characterization of nonreciprocity of spin waves.
The time resolved measurement of surface spin waves for three bias magnetic fields of ±60 Oe (a), ±135 Oe (b) and ±200 Oe (c). An excitation impulse voltage of 1.6 V with a pulse width of ~80 ps has been used. Micromagnetic simulation results of surface spin waves at ±60 Oe (d), ±135 Oe (e) and ±200 Oe (f).
Logic gates using nonreciprocal spin wave propagation
Here, we propose spin wave logic gates to implement any Boolean function. A cross-section image of a NOT gate or a PASS gate can be seen in Fig. 4(a) and the top view image of the device structure is shown in Fig. 4(b). We assume that the ferromagnetic structure has an anisotropy with an easy-axis in the y-direction, which can be easily implemented by material engineering during the film growth39,40. Once the input A is a logic 1, the Oersted field generated by the input A-line is strong enough to switch the magnetization of the ferromagnetic film to the −y-direction. When the input A is a logic 0, the Oersted field generated by the input A-line favors the magnetization to be aligned in the +y-direction. The device has two outputs (Y and  ) complementary to each other. If the effective field is in the +y-direction, the spin wave excited by the narrow current pulse of triggering signal I generates a larger amplitude in Y than
) complementary to each other. If the effective field is in the +y-direction, the spin wave excited by the narrow current pulse of triggering signal I generates a larger amplitude in Y than  . For an effective field in the −y-direction, the output
. For an effective field in the −y-direction, the output  has larger amplitudes than Y. The truth table of the logic circuit is shown in Fig. 4(c). The output Y implements a NOT gate, while the
has larger amplitudes than Y. The truth table of the logic circuit is shown in Fig. 4(c). The output Y implements a NOT gate, while the  implements a PASS gate.
implements a PASS gate.
Logic gates using nonreciprocal spin wave propagation.
The spin wave logic based on the spin wave nonreciprocal behavior. The schematic diagram of the cross section view (a) and the top view (b) of logic device structure for one input (A) and two complementary outputs (Y and  ). (c) The truth table of the logic gate with the corresponding Boolean expression for each output that resembles a NOT gate for the Y output and a PASS gate for the
). (c) The truth table of the logic gate with the corresponding Boolean expression for each output that resembles a NOT gate for the Y output and a PASS gate for the  port. The schematic diagram of the cross section view (d) and the top view (e) of the device structure for two-input (A and B) logic gate. (f) The truth table and Boolean expressions of the two-input logic gate.
port. The schematic diagram of the cross section view (d) and the top view (e) of the device structure for two-input (A and B) logic gate. (f) The truth table and Boolean expressions of the two-input logic gate.
We can also implement a two-input logic circuit as shown in Fig. 4(d–e). The magnetic film has an easy-axis in the y-direction with an anisotropy field of Hb. The input A generates a field large enough to switch the ferromagnetic film in the −y-direction, while the input B generates a field in the +y-direction. The truth-table of the logic circuit is shown in Fig. 4(f) with corresponding schematics of logic gates. The Boolean expression of the output Y can be written as  , which is a combination of NOT and OR gates. We can build all the logic gates with the help of the proposed one-input and two-input gates (Supplementary Information S6). Therefore, the proposed logic gates are a complete logic system to build any Boolean function. For a short pulse excitation in the triggering signal I, the output signal is a spin wave packet that can be reshaped using a standard push-detection circuit commonly used in the rf systems, therefore, the output signal can be fed as an input for the other gates (Supplementary Information S7).
, which is a combination of NOT and OR gates. We can build all the logic gates with the help of the proposed one-input and two-input gates (Supplementary Information S6). Therefore, the proposed logic gates are a complete logic system to build any Boolean function. For a short pulse excitation in the triggering signal I, the output signal is a spin wave packet that can be reshaped using a standard push-detection circuit commonly used in the rf systems, therefore, the output signal can be fed as an input for the other gates (Supplementary Information S7).
Discussion
The triggering signal I can be used as a clock for the synchronization of different gates, therefore depending on the propagation delay of the spin wave and the delay of the wave-shaping circuit, the maximum operational frequency of the logic gate can be determined. The surface spin wave has a very large group velocity (vg ~ a few tens of μm/ns)23. Furthermore, the push-detector circuit can operate in the GHz range (See for example LMH2110 power detector chip). Therefore, the logic gate can easily operate in the GHz frequency ranges. In addition, the device is scalable and the performance of the device can be even enhanced in low dimensions (Supplementary Information S8). We have designed logic gates with a feature size of 10 and 100 nm for a width of the ferromagnetic structure as an example of the scalability of the device (Supplementary Information S9). In terms of power consumption, the spin wave propagation does not involve any charge transfer, therefore it is an energy efficient logic scheme. The triggering signal I can be a very short pulse (<80 ps) as it is demonstrated in our experiments and the driving current of I can be very small (<1 mA) since the field induced by I is inversely proportional to the width of the strip line. In addition, our spin wave logic has some degrees of non-volatility such that the magnetization direction of the ferromagnetic structure is preserved in the ±y directions, when the device power is turned off.
In summary, the nonreciprocal behavior of spin waves has been experimentally studied in both frequency and time domains. It is found that the nonreciprocity factor is not constant and can be tuned by the bias magnetic field. Based on the findings, a new type of spin wave based logic devices has been proposed that utilizes the spin wave amplitude for its operations. We show that our logic system is complete and can implement all the Boolean functions. Our proposed logic circuit operates in GHz ranges with very low power dissipation and paves a way to the future spin-based logic devices.
Methods
Device fabrication
A 20 nm thick permalloy film is dc-sputtered at room temperature on Si/SiO2 (300 nm) substrates. After coating the substrate with a negative-tone e-beam resist, the resist are patterned into different structures with a length of 200 μm and the width ranging from 1 to 400 μm. In the case of small wires (width < 11 μm), multiple wires with a spacing of 1 μm and a total width of 400 μm are patterned. The patterns are transferred to the ferromagnetic film using Ar ion milling and then the resist is removed. Using ac-magnetron sputtering, a 50 nm thick SiO2 layer is deposited for the isolation of the ferromagnetic structure from the waveguides. Using the second e-beam lithography step with a positive-tone resist, the asymmetric coplanar waveguides are patterned followed by the deposition of Cr (5 nm)/Ag (150 nm)/Pt (5 nm) and lift-off.
Measurements
The samples are characterized in a homemade high frequency probe station with in-situ magnetic fields (up to 6 kOe) and using GSG probes from GGB Industries, Inc. For the frequency-domain characterization of spin waves, we utilize an Agilent N5245A microwave network analyzer with an excitation power of 5 dBm. Before frequency-domain characterization, the effects of cables and connectors are compensated using a CS-5 calibration substrate from GGB Industries, Inc. For time-domain characterization, we utilize an 86100A Infiniium wide-bandwidth sampling oscilloscope. The pulses are generated using a Centellax PPG12500 pulse/pattern generator with an amplitude of 1.6 V. Before capturing of spin waves, the signal is amplified by 29 dB using a SHF810 low noise preamplifier.
References
Vogel, E. Technology and metrology of new electronic materials and devices. Nature Nanotechnol. 2, 25–32 (2007).
Tamir, D. E., Shaked, N. T., Wilson, P. J. & Dolev, S. High-speed and low-power electro-optical DSP coprocessor. J. Opt. Soc. Am. A 26, A11–A20 (2009).
Caulfield, H. J. & Dolev, S. Why future supercomputing requires optics. Nature Photon. 4, 261–263 (2010).
Wang, L. & Li, B. Thermal logic gates: computation with phonons. Phys. Rev. Lett. 99, 177208 (2007).
Behin-Aein, B., Salahuddin, S. & Datta, S. Switching energy of ferromagnetic logic bits. IEEE Trans. Nanotech. 8, 505–514 (2009).
Augustine, C., Fong, X. Y., Behin-Aein, B. & Roy, K. Ultra-low power nanomagnet-based computing: a system-level perspective. IEEE Trans. Nanotech. 10, 778–788 (2011).
Khitun, A., Ostroumov, R. & Wang, K. L. Spin-wave utilization in a quantum computer. Phys. Rev. A 64, 062304 (2001).
Wesenberg, J. H. et al. Quantum computing with an electron spin ensemble. Phys. Rev. Lett. 103, 070502 (2009).
Wolf, S. A. et al. Spintronics: a spin-based electronics vision for the future. Science 294, 1488–1495 (2001).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Cowburn, R. P. & Welland, M. E. Room temperature magnetic quantum cellular automata. Science 287, 1466–1468 (2000).
Imre, A. et al. Majority logic gate for magnetic quantum-dot cellular automata. Science 311, 205–208 (2006).
Ney, A., Pampuch, C., Koch, R. & Ploog, K. H. Programmable computing with a single magnetoresistive element. Nature 425, 485–487 (2003).
Allwood, D. A. et al. Magnetic domain-wall logic. Science 309, 1688–1692 (2005).
Nakano, K. et al. All-electrical operation of magnetic vortex core memory cell. Appl. Phys. Lett. 99, 262505 (2011).
Xu, P. et al. An all-metallic logic gate based on current-driven domain wall motion. Nature Nanotechnol. 3, 97–100 (2008).
Behin-Aein, B., Datta, D., Salahuddin, S. & Datta, S. Proposal for an all-spin logic device with built-in memory. Nature Nanotechnol. 5, 266–270 (2010).
Dery, H., Dalal, P., Cywinski, L. & Sham, L. J. Spin-based logic in semiconductors for reconfigurable large-scale circuits. Nature 447, 573–576 (2007).
Schneider, T. et al. Realization of spin-wave logic gates. Appl. Phys. Lett. 92, 022505 (2008).
Lee, K.-S. & Kim, S.-K. Conceptual design of spin wave logic gates based on a Mach-Zehnder-type spin wave interferometer for universal logic functions. J. Appl. Phys. 104, 053909 (2008).
Mathieu, C. et al. Lateral quantization of spin waves in micron size magnetic wires. Phys. Rev. Lett. 81, 3968–3971 (1998).
Walker, L. R. Magnetostatic modes in ferromagnetic resonance. Phys. Rev. 105, 390–399 (1957).
Covington, M., Crawford, T. M. & Parker, G. J. Time-resolved measurement of propagating spin waves in ferromagnetic thin films. Phys. Rev. Lett. 89, 237202 (2002).
Silva, T. J., Lee, C. S., Crawford, T. M. & Rogers, C. T. Inductive measurement of ultrafast magnetization dynamics in thin-film Permalloy. J. Appl. Phys. 85, 7849–7862 (1999).
Bailleul, M., Olligs, D. & Fermon, C. Propagating spin wave spectroscopy in a permalloy film: A quantitative analysis. Appl. Phys. Lett. 83, 972–974 (2003).
Kwon, J. H., Mukherjee, S. S., Jamali, M., Hayashi, M. & Yang, H. Spin waves interference from rising and falling edges of electrical pulses. Appl. Phys. Lett. 99, 132505 (2011).
Mukherjee, S. S., Kwon, J. H., Jamali, M., Hayashi, M. & Yang, H. Interference-mediated modulation of spin waves. Phys. Rev. B 85, 224408 (2012).
Mukherjee, S. S., Deorani, P., Kwon, J. H. & Yang, H. Attenuation characteristics of spin-pumping signal due to traveling spin waves. Phys. Rev. B 85, 094416 (2012).
Kwon, J. H., Mukherjee, S. S., Deorani, P. M., Hayashi, M. & Yang, H. Characterization of magnetostatic surface spin waves in magnetic thin films: evaluation for microelectronic applications. Appl. Phys. A 111, 369–378 (2013).
Kostylev, M. P., Serga, A. A., Schneider, T., Leven, B. & Hillebrands, B. Spin-wave logical gates. Appl. Phys. Lett. 87, 153501 (2005).
Khitun, A. & Wang, K. L. On logic circuits with spin wave bus. J. Nanoelectron. Optoelectron. 1, 71–73 (2006).
Hertel, R., Wulfhekel, W. & Kirschner, J. Domain-wall induced phase shifts in spin waves. Phys. Rev. Lett. 93, 257202 (2004).
Bandyopadhyay, S. & Cahay, M. Electron spin for classical information processing: a brief survey of spin-based logic devices, gates and circuits. Nanotechnology 20, 412001 (2009).
Damon, R. W. & Eshbach, J. R. Magnetostatic modes of a ferromagnetic slab. J. Phys. Chem. Sol. 19, 308–320 (1961).
Schneider, T., Serga, A. A., Neumann, T., Hillebrands, B. & Kostylev, M. P. Phase reciprocity of spin-wave excitation by a microstrip antenna. Phys. Rev. B 77, 214411 (2008).
Amiri, P. K., Rejaei, B., Vroubel, M. & Zhuang, Y. Nonreciprocal spin wave spectroscopy of thin Ni-Fe stripes. Appl. Phys. Lett. 91, 062502 (2007).
Sekiguchi, K. et al. Nonreciprocal emission of spin-wave packet in FeNi film. Appl. Phys. Lett. 97, 022508 (2010).
Demidov, V. E., Urazhdin, S. & Demokritov, S. O. Control of spin-wave phase and wavelength by electric current on the microscopic scale. Appl. Phys. Lett. 95, 262509 (2009).
Wilts, C. H. & Humphrey, F. B. Magnetic anisotropy in flat ferromagnetic films: a review. J. Appl. Phys. 39, 1191–1196 (1968).
Heinrich, B. et al. Development of magnetic anisotropies in ultrathin epitaxial films of Fe(001) and Ni(001). Appl. Phys. A 49, 473–490 (1989).
Acknowledgements
This work is partially supported by the Singapore Ministry of Education Academic Research Fund Tier 1 (R-263-000-A46-112) and Singapore National Research Foundation under CRP Award No. NRF-CRP 4-2008-06.
Author information
Authors and Affiliations
Contributions
M.J. and H.Y. conceived the experiments. M.J. and J.K. carried out experiments. M.J., S.S. and K.L. did simulations. M.J. and H.Y. wrote the manuscript. All authors discussed the data and the results and commented the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary info
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Jamali, M., Kwon, J., Seo, SM. et al. Spin wave nonreciprocity for logic device applications. Sci Rep 3, 3160 (2013). https://doi.org/10.1038/srep03160
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03160
This article is cited by
-
Accumulation and control of spin waves in magnonic dielectric microresonators by a comb of ultrashort laser pulses
Scientific Reports (2022)
-
Inverse-design magnonic devices
Nature Communications (2021)
-
Tunable asymmetric spin wave excitation and propagation in a magnetic system with two rectangular blocks
Scientific Reports (2021)
-
A nonlinear magnonic nano-ring resonator
npj Computational Materials (2020)
-
Efficient wavelength conversion of exchange magnons below 100 nm by magnetic coplanar waveguides
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.