Abstract
Large numbers of transients visit big cities, where they come into contact with many people at crowded areas. However, epidemiological studies have not paid much attention to the role of this subpopulation in disease spread. We evaluate the effect of transients on epidemics by extending a synthetic population model for the Washington DC metro area to include leisure and business travelers. A synthetic population is obtained by combining multiple data sources to build a detailed minute-by-minute simulation of population interaction resulting in a contact network. We simulate an influenza-like illness over the contact network to evaluate the effects of transients on the number of infected residents. We find that there are significantly more infections when transients are considered. Since much population mixing happens at major tourism locations, we evaluate two targeted interventions: closing museums and promoting healthy behavior (such as the use of hand sanitizers, covering coughs, etc.) at museums. Surprisingly, closing museums has no beneficial effect. However, promoting healthy behavior at the museums can both reduce and delay the epidemic peak. We analytically derive the reproductive number and perform stability analysis using an ODE-based model.
Similar content being viewed by others
Introduction
Influenza places a huge annual burden on society. It is estimated that, in the US alone, the total annual economic burden of influenza epidemics amounts to $87.1 billion1. In order to develop and implement effective interventions to reduce the spread of influenza, it is necessary to understand the interaction patterns within the population and the consequences of interventions on these interactions.
Population mixing patterns can be very complex, especially in large cities, in part because the population itself fluctuates significantly over time. Big cities attract a large number of transients, such as tourists and business travelers. For example, Washington DC is estimated to have 50,000 transients each day on average. They usually visit high traffic areas in the city and come into contact both with each other and also with area residents. Hence they may reasonably be expected to play a significant role in spreading disease. However, most epidemiological modeling studies have ignored the role of this subpopulation in epidemics. In the present work we explore the impact of transient populations—tourists and business travelers—on influenza-like illnesses (ILI) in Washington DC. We also evaluate intervention strategies targeted at major tourism locations where a lot of mixing happens.
Our approach uses two complementary techniques. In the first, we develop a synthetic population-based model that we use to simulate resident and transient activities in detail in order to model their interactions. Synthetic population-based models have been widely used to study epidemics and epidemic interventions, for example, to study the vulnerability of individuals to contract the infection3,5 and to study the effect of interventions such as social distancing and vaccination distribution6,7. In addition, given the synthetic population-based model and the individual's activity patterns, we can obtain a synthetic social network reflecting the dynamical contact patterns of individuals during a time period. This approach is preferable to study the spread of infectious diseases than the assumption of a static social network8.
Simulations with and without the transient population allow us to quantify the difference in epidemic characteristics such as the attack rate and the day of the peak in the epidemic curve that are due to the transients. In the second approach, we develop several ordinary differential equation (ODE) based models to derive quantities such as the reproductive number and fixed points. Mixing rates required for these models are calibrated to contact patterns induced by the synthetic population model. We also model interventions centered on four major tourist destinations around the National Mall.
Very few studies have been done to understand the effect of transient populations on epidemics. Ferguson et al.9 have modeled air travel for the United States and Great Britain but they assumed that tourists stay at hotels and do not travel within the city. Hence in these models the only place transients come in contact with residents is at hotels. However, in big cities like Washington DC, there are some popular tourist destinations that many tourists visit and are highly crowded. For example, the National Air and Space Museum in Washington DC has more than 80,000 visits every day. Tourists come into contact with many people, including both residents and other tourists, at these places. Intuitively, this can have a significant impact on an epidemic because transient subpopulations serve as a constant reservoir of susceptible people (as there is a constant flux of new transients).
In addition to9, there are many deterministic and stochastic approaches addressed the effect of transients using metapopulation networks17,18,19,20,21,22,23,24,25,26. A common assumption with these models is the homogeneous mixing among subpopulations. However, it is not necessary that every individual in a subpopulation has contacts with individuals from other subpopulations. Through the individual-based model, we will show that the mixing among subpopulations is heterogeneous and the number of residents who are in contact with the transient subpopulation is less than the total number of residents.
Here, we extend a synthetic population model for the Washington DC Metro Area to include a transient population consisting of leisure and business travelers. This population was constructed by combining data from Destination DC10, the Smithsonian Institution and other geo-spatial data (detailed in the Supplementary Information ). We simulate an influenza-like illness (ILI) for the Washington DC metro area both with and without transients to evaluate their effect. Results show that transients do indeed have a significant impact on disease dynamics of the city.
Since some tourist destinations attract very large numbers of visitors each day, they present a natural target for interventions. We evaluate two kinds of interventions: closing major tourist destinations (the four most visited museums around the National Mall), which is an attempt at social distancing; and a “healthy behavior” intervention, which represents a temporary, location-specific reduction in transmission rates, where we assume that promoting sanitary habits at these locations, such as hand hygiene, covering your cough and other behavioral measures, can reduce the spread of the disease at these locations. We find that, on the one hand, surprisingly, closing the museums does not help. On the other hand, the healthy behavior intervention, even applied temporarily to only half the visitors at fairly low efficacy, can make a significant difference in the epidemic. In addition to the agent-based simulation, we study the spread of the epidemic analytically using a system of parameterized ODEs, by assuming homogeneous mixing within and between resident and transient populations. We extract the contact matrix and the duration of every contact from the synthetic social network and derive the average number of contacts per day per individual (contact rate) and the average duration per contact. These are used to calibrate the ODEs' mixing rate parameters, which are used to find the reproductive number analytically. This number reflects how far the system resides from the epidemic-free scenario.
We also use the ODE model to perform stability analysis, determining the conditions for epidemic-free equilibrium, asymptotic epidemic die-out and permanently endemic equilibrium. Moreover, the synthetic social network reveals the actual mixing between residents and transients. For instance, not every resident has contact with transients. Consequently, the ODE model is refined by dividing the resident population into two subpopulations, which in turn leads to a refinement for the reproductive number. A further refinement of the ODE model is used to evaluate the impact of the two different intervention strategies. Results obtained from the ODE model are qualitatively similar to the agent-based simulation results.
Results
We summarize our results here, before describing them in detail further below.
Our simulations show that the presence of transients has a statistically significant impact on the number of resident infections at peak (making them almost 23% higher), the number of resident infections over the course of the epidemic (making them 9% higher) and the time when the disease peaks (making it about 10 days earlier).
We model interventions aimed at the four most-visited locations around the National Mall. Our simulations show that closing these locations for a short period (we considered two scenarios, involving closing these locations for 5 days or 14 days) does not help. This is likely because the tourists who would have visited these locations go to other, smaller, tourist destinations and residents who would have visited these locations continue their other activities and hence there is still considerable mixing among these populations.
On the other hand, the “healthy behavior” intervention can significantly reduce the epidemic, depending on the efficacy of the intervention at reducing transmission within those four locations. We assume a compliance rate of 50%, i.e., only half the visitors to these locations engage in healthy behavior. We find that if the intervention has the effect of reducing infectivity and susceptibility within these locations to 80%, 60%, 40% or 20% of the value without sanitizer use, it can delay the peak by 2 to 7 weeks. The number of residents infections at peak is reduced by 6% to 37.5% and the cumulative number of resident infections over 120 days is reduced by 3.6% to 34.6%.
We also develop three successively refined ODE models. The first considers only two compartments, corresponding to residents and transients. Since the transients only stay in the city for a short while (5 days on average), there is a birth-death process associated with this compartment. We use this model to derive the effective reproductive number for the system, as a function of the transmission rates of the subpopulations. Surprisingly, even if the reproductive number for each subpopulation is less than 1, the overall R0 can be greater than 1, leading to an epidemic.
Since not all residents come into contact with transients, we refine the model to create separate compartments for residents who do and do not come into contact with transients. Since all transients come into contact with residents, we do not need to split that compartment. Analysis of this model shows that the most effective means of reducing the reproductive number below 1 (thereby eliminating the epidemic) is to reduce the contact rate between transients and residents. Reducing the contact rate between residents who do and do not come into contact with transients is not enough to reduce the reproductive number below 1.
Third, in order to analyze the healthy behavior intervention, we further refine the ODE model to create compartments corresponding to the people who go to the intervention locations and those who do not. For compliance rate of 50%, if the transmissibility is reduced to 20% and 40% of its value without the practice of healthy behavior, the reproductive number is reduced by 36% and 27%, respectively. We also find that the largest reduction of reproductive number is 58% when the compliance rate and the reduction of transmissibility are 100%. In addition, given higher compliance rates, the reduction of reproductive number exhibits a nonlinear response with the efficacy of healthy behavior.
Effect of transients
A synthetic population is a disaggregated (“agent-based”) representation of the population of a region. It is constructed by combining data from multiple sources, such as the American Community Survey, the National Household Travel Survey, Navteq, Dun & Bradstreet, the National Center for Education Statistics and others. Together these datasets provide information about demographics, activity times and durations and activity locations. A synthetic population, therefore, is a model of who people are, where they go during the course of a day and consequently, with whom they come into contact. This allows the induction of a synthetic social contact network, which is a model of the network over which disease propagation happens. This approach has been used for computational epidemiology for more than a decade11.
We simulate an influenza-like illness (ILI) over the synthetic social contact network for the Washington DC metro area. We simulate the disease spread for 120 days both with and without the transient population. Initial infections are the same for all cases. Only residents are initially infected. Transients are assumed not to bring disease to the city, though they can get infected during their stay in the area and, after an incubation period, pass the infection on to others. This is a best-case scenario – if we assume that a (small) fraction of transients are infected when they arrive, epidemic outcomes are worse. To simplify the model, transients are assumed to stay in the city for exactly five days, which is the average length of a trip according to data from Destination DC. When they leave, they are assumed to be replaced by new incoming susceptible transients with exactly the same demographics and activity schedules. Though somewhat unrealistic, this greatly simplifies the computational implementation of the model.
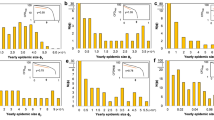
As we are interested in the effect of transients on the number of residents being infected, Figures 1, 2 and 3 show scatter plots for the fraction of residents infected at peak, the fraction of residents infected cumulatively over the simulation period (120 days) and the day when the the disease peaks, respectively. This helps to show the differences in the variances of different scenarios and motivates our choice of statistical tests (see Supplementary information for details on statistical tests). We also create box plots for the fraction of the resident population currently infected at peak (Figure 4), the fraction of the resident population infected cumulatively over 120 days (Figure 5) and the day of peak (Figure 6). The simulations show that the disease peaks about 10 days earlier and there are about 23% more resident infections on average at peak when the transients are considered. Over the period of 120 days, 9% more residents are infected. All these differences are statistically significant (t-test, α = 0.05, Supplementary Information ). Specifically the difference in the number of the number of infections at peak is very important from a public health perspective because it determines elements of response such as the number of beds required in hospitals.
Scatter plots showing the fraction of residents infected at peak vs. group where groups are defined as follows: 1 - No interventions (residents only), 2 - Museums closed for 5 days (residents only), 3 - Museums closed for 14 days (residents only), 4 - Healthy Behavior 80% (residents only), 5 - Healthy Behavior 60% (residents only), 6 - Healthy Behavior 40% (residents only), 7 - Healthy Behavior 20% (residents only), 8 - No interventions (residents + transients), 9 - Museums closed for 5 days (residents + transients), 10 - Museums closed for 14 days (residents + transients), 11 - Healthy Behavior 80% (residents + transients), 12 - Healthy Behavior 60% (residents + transients), 13 - Healthy Behavior 40% (residents + transients), 14 - Healthy Behavior 20% (residents + transients).
It gives an idea about the variances for each group. For statistically comparing various groups ( supplementary information ), we remove outliers from each group.
Scatter plots showing the fraction of residents infected cumulatively vs. group where groups are defined as follows: 1 - No interventions (residents only), 2 - Museums closed for 5 days (residents only), 3 - Museums closed for 14 days (residents only), 4 - Healthy Behavior 80% (residents only), 5 - Healthy Behavior 60% (residents only), 6 - Healthy Behavior 40% (residents only), 7 - Healthy Behavior 20% (residents only), 8 - No interventions (residents + transients), 9 - Museums closed for 5 days (residents + transients), 10 - Museums closed for 14 days (residents + transients), 11 - Healthy Behavior 80% (residents + transients), 12 - Healthy Behavior 60% (residents + transients), 13 - Healthy Behavior 40% (residents + transients), 14 - Healthy Behavior 20% (residents + transients).
It gives an idea about the variances for each group. For statistically comparing various groups ( supplementary information ), we remove outliers from each group.
Scatter plots showing the day of peak vs. group where groups are defined as follows: 1 - No interventions (residents only), 2 - Museums closed for 5 days (residents only), 3 - Museums closed for 14 days (residents only), 4 - Healthy Behavior 80% (residents only), 5 - Healthy Behavior 60% (residents only), 6 - Healthy Behavior 40% (residents only), 7 - Healthy Behavior 20% (residents only), 8 - No interventions (residents + transients), 9 - Museums closed for 5 days (residents + transients), 10 - Museums closed for 14 days (residents + transients), 11 - Healthy Behavior 80% (residents + transients), 12 - Healthy Behavior 60% (residents + transients), 13 - Healthy Behavior 40% (residents + transients), 14 - Healthy Behavior 20% (residents + transients).
It gives an idea about the variances for each group. For statistically comparing various groups ( supplementary information ), we remove outliers from each group.
Comparison of various scenarios (residents only, residents + transients and two intervention strategies, closing museums (four most-visited locations) and practice of healthy behavior (at these museums with the compliance rate of 50%), with 50 simulations for each case) in terms of the fraction of residents infected at peak as shown in the box plot.
Significantly more residents are infected at peak when transients are considered (see Supplementary Information for the statistical significance of the differences). Closing four major tourism locations does not reduce the peak number infected (in the presence or absence of transients). This might be because we assume that when museums are closed, transients go to other tourism places and residents continue other activities and hence there is still considerable mixing. However, practice of healthy behavior at these museums could make a significant difference (both in the presence and absence of transients), depending upon how much it reduces the person-person transmission rate.
Comparison of various scenarios (residents only, residents + transients and two intervention strategies, closing museums (four most-visited locations) and practice of healthy behavior (at these museums with the compliance rate of 50%), with 50 simulations for each case) in terms of the fraction of residents infected cumulatively over 120 days as shown in the box plot.
There are more residents infected over the period of 120 days when transients are considered. Once again, closing museums does not help. Reducing person-person transmission rate at the same locations to 60% of its nominal value for only half the visitors could be almost as good as removing transients entirely. Reducing transmission rates further to 40% or 20%, makes an even bigger difference. The results in the absence of transients are similar to the results in the presence of transients.
Comparison of various scenarios (residents only, residents + transients and two intervention strategies, closing museums (four most-visited locations) and practice of healthy behavior (at these museums with the compliance rate of 50%), with 50 simulations for each case) in terms of the day of peak prevalence as shown in the box plot.
The presence of a transient population in the city makes the outbreak peak earlier as compared to a scenario with residents only. Closing major museums does not delay the peak (both in the presence and absence of transients). However, using promoting healthy behavior at these museums could delay the outbreak considerably (2 to 5 weeks in the presence of transients and about 10 days to at least a couple of months (disease does not reach peak during the simulation period of 12 days when efficacy is assumed to be 40% and 20%) in the absence of transients).
Analysis
We study a corresponding ODE (SEIR) model with two compartments, residents and transients. As transients are assumed to stay for 5 days in the city, there is a birth and death process for transients with rate ρ = 0.2. Given the synthetic social network which is composed of contacts among individuals and the duration of each contact, we can compute the average contact rate and the average duration per contact between resident and transient populations. These computed values are used to set the parameters of the ODE model.
The average contact rate and duration per contact for a resident individual with other residents are 99.7 contacts per day and 0.62 hours, respectively. On the other hand, the contact rate and duration per contact for a resident individual with transients are 242.9 contacts per day and 0.11 hours, respectively. In addition, the contact rate and duration per contact for a transient individual with residents are 4010.8 contacts per day and 0.11 hours, respectively. The contact rate between a transient individual and other transients is 719.14 contacts per day and the average duration of each contact is 0.15 hours. Using the next generation method12,13, the overall reproductive number (also reported by14) for the system is given by,

where  and
and  are the reproductive numbers for the resident and transient populations, respectively. The rates βr→r and βt→t are the infection transmission rates within resident and transient population, respectively. The rate βr→t represents the infection rate from transients to a single resident, while the rate βt→r represents the infection rate from residents to a single transient. Rates γ and μ are the rates at which an exposed individual becomes infected and an infected individual recovers, respectively. The term
are the reproductive numbers for the resident and transient populations, respectively. The rates βr→r and βt→t are the infection transmission rates within resident and transient population, respectively. The rate βr→t represents the infection rate from transients to a single resident, while the rate βt→r represents the infection rate from residents to a single transient. Rates γ and μ are the rates at which an exposed individual becomes infected and an infected individual recovers, respectively. The term  is called the competing reproductive number (
is called the competing reproductive number ( ), which represents the average number of secondary infected cases in a susceptible population caused by an infected individual from the other population.
), which represents the average number of secondary infected cases in a susceptible population caused by an infected individual from the other population.
Using the Jacobian matrix for the homogeneous mixing differential equations, we derive the competing reproductive number by assuming that there is no mixing within each population, i.e. βr→r = βt→t = 0. Details about the Jacobian matrix and the derivation can be found in the Supplementary Information .
The system of differential equations has three equilibrium points:
-
1
Disease-free equilibrium point Ro < 1, where initially infected cases recover without causing a cascade of new infections. In this case, the two populations are susceptible at equilibrium.
-
2
Asymptotic epidemic die-out point Ro > 1 and
 , where the disease spreads in both populations. At equilibrium, residents are either susceptible or recovered and transients are susceptible because infected transients leave the city and are replaced by susceptible transients, while the transient reproductive number is below 1.
, where the disease spreads in both populations. At equilibrium, residents are either susceptible or recovered and transients are susceptible because infected transients leave the city and are replaced by susceptible transients, while the transient reproductive number is below 1. -
3
Transient endemic point Ro > 1 and
 , where the disease persists in the transient population. Due to the assumption that every resident has contacts with transients, all residents eventually contract the infection and recover. However, the synthetic social network reveals the fact that not all residents meet transients. Therefore, a more detailed model is introduced to distinguish between residents who have contacts with residents only and residents who have contacts with residents and transients.
, where the disease persists in the transient population. Due to the assumption that every resident has contacts with transients, all residents eventually contract the infection and recover. However, the synthetic social network reveals the fact that not all residents meet transients. Therefore, a more detailed model is introduced to distinguish between residents who have contacts with residents only and residents who have contacts with residents and transients.
The visit time duration has an impact on the overall attack rate for transients and residents. Thus, we study the sensitivity of the overall attack rate with respect to the visit duration and we find that the attack rate increases nonlinearly as the visit duration becomes longer as shown in the
Supplementary Information
. We study the sensitivity of the overall reproductive number and the attack rate with respect to all four infection transmission rates on which they depend. We evaluate the overall reproductive number and the attack rate as a function of two infection rates, while fixing the other two infection rates at their estimated values for the following cases: Ro as a function of  and
and  , Ro as a function of
, Ro as a function of  and
and  , Ro as a function of
, Ro as a function of  and
and  , Ro as a function of
, Ro as a function of  and
and  and Ro as a function of
and Ro as a function of  and
and  .
.
The first case is shown in Figures 7 and 8 and the other four cases are shown in the
Supplementary Information
. In Figure 7, even if the reproductive numbers  and
and  are less than 1, the overall reproductive number Ro can be greater than 1 and the epidemic spreads in the two populations. This observation is consistent with the non-endemic disease equilibrium point where there is no endemic equilibrium for the transient population. The endemic equilibrium point is observed for
are less than 1, the overall reproductive number Ro can be greater than 1 and the epidemic spreads in the two populations. This observation is consistent with the non-endemic disease equilibrium point where there is no endemic equilibrium for the transient population. The endemic equilibrium point is observed for  and the corresponding attack rate becomes high (~0.45). Also the two figures show that the transient reproductive number changes slower than the resident reproductive number when their infection rates are changed similarly between 0 and 2.
and the corresponding attack rate becomes high (~0.45). Also the two figures show that the transient reproductive number changes slower than the resident reproductive number when their infection rates are changed similarly between 0 and 2.
Evaluation of the reproductive number Ro in eqn.1 as a function of the resident reproductive number  and transient reproductive number
and transient reproductive number  while the competing reproductive number
while the competing reproductive number  equals its estimated value 0.5359.
equals its estimated value 0.5359.
The reproductive number is evaluated by sweeping the infection rates values βr→r and βt→t between 0 and 2 and changing  and
and  accordingly.
accordingly.
Evaluation of the attack rate as a function of the resident reproductive number  and transient reproductive number
and transient reproductive number  while the competing reproductive number
while the competing reproductive number  equals its estimated value 0.5359.
equals its estimated value 0.5359.
The attack rate is evaluated by sweeping the infection rates values βr→r and βt→t between 0 and 2 and changing  and
and  accordingly and evaluate the final number of infected residents and transients.
accordingly and evaluate the final number of infected residents and transients.
A more detailed model
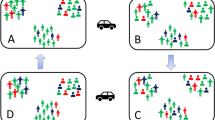
The above model considers homogeneous mixing between resident and transient populations. But not all residents meet transients – in the synthetic population model, out of 4.1 million residents, only ~734,000 residents meet transients. Thus, we divided the two populations into four subpopulations: residents who meet residents only (denoted by rr in the following), residents who meet residents and transients (rt), transients who meet transients only (tt) and transients who meet transients and residents (tr).
In the synthetic population model, all transients come in contact with residents. Therefore, the subpopulation of transients who only meet transients is not considered, i.e., tt = 0. The contact pattern and the infection transmission rates among these four subpopulations are as shown in Figure 9. There are ten infection transmission rates in the model, of which three are zero because tt = 0, as shown in Figure 9. The remaining seven non-zero transmission rates are used to find a new reproductive number Ro.
Contact pattern among four subpopulations.
In general, βab→cd represents the infection transmission rate due to the contact between subpopulation ab to subpopulation cd. The infection rates βrr→rr, βrr→rt, βrt→rr, βrt→rt, βrt→tr, βtr→rt and βtr→tr have positive values, while the infection rates βtt→tt, βtt→tr and βtr→tt equal 0 because all transients have contacts with both transients and residents. That is, the population tt represented by the red oval in the lower left vanishes.
To study the effect of each infection transmission rate on the reproductive number, we sweep the value of a single infection rate between 0 and 2, while the other infection rates are kept constant at their estimated values. In Figure 10, we show the reproductive number as a function of infection rates βrr→rr, βrt→tr and βtr→rt (the four-letter subscripts indicate the two subpopulations that are coming into contact). The figure shows that reducing the infection transmission rates between residents who have contacts with transients (rt) and transients (tr), βrt→tr and βtr→rt, is the most effective strategy to reduce the reproductive number below 1. On the other hand, reducing the infection rate among residents who only have contacts with other residents βrr→rr slightly reduces the reproductive number, but it remains above 1. In the Supplementary Information , we also evaluate the reproductive number as a function of βrr→rt, βrt→rr, βrt→rt and βtr→tr. Epidemic results obtained from the ODE model using four subpopulation, using contact rates obtained from the synthetic social contact network, are qualitatively similar to the simulation results.
Evaluation of reproductive number as a function of the infection transmission rates.
The circles represent the estimated infection transmission rate values based on the synthetic social network. The thin dash line represents the value of reproductive number Ro = 1.375, while the thick dash line represents reproductive number Ro = 1 below which the epidemic dies out. For every infection transmission rate, we sweep the transmission rate value between 0 and 2 and we evaluate the reproductive number Ro using eq. in the Supplementary Information , while the remaining transmission rates are fixed at their estimated values.
Intervention strategies
We study different intervention strategies using both agent-based model and ODE model. Starting with the agent-based model, to investigate the intuition that major tourist locations like the National Air and Space Museum (NASM), the National Museum of Natural History (NMNH), the National Museum of American History (NMAH) and the National Gallery of Art (NGA), which have about 40000 to 80000 visits (including visits from residents and transients) per day, have a big impact on the epidemic, we looked at the infections which happen at these locations. In a simulation this is straightforward to track, though of course, this cannot be determined in reality. We find that the number of infections at these four locations are approximately doubled when transients are considered ( Supplementary Information ). Also, as the transients stay for a short period of time and at the end of their trips, new, uninfected, but susceptible transients replace them, there is an almost constant number of susceptible and infected people at these locations, making them prominent sites for infection. This leads us to investigate interventions focused at these locations for reducing the epidemic.
Closing museums
A commonly studied intervention to reduce infections is to apply social distancing measures like closing schools, work places etc., which reduces mixing and hence infections. Here, as we are interested in reducing the impact of transients, we model closing the four big museums for a few days when the number of infections reaches a threshold. We assume that when museums are closed tourists go to other tourist locations and residents visiting these museums go back to their normal daily schedules. We simulate two cases:
-
When the current number of infections (residents + transients) reaches 50,000, we close these museums the next day for 5 days.
-
When the current number of resident infections reaches 50,000, we close these museums the next day for 14 days.
There are about 12.5% and 14.5% more resident infections (statistically significant, see supplementary information ) at peak when museums are closed for 5 days and 14 days, respectively. Over the period of 120 days, there are 9% and 8.8% more residents infected (though not statistically significant) when museums are closed for 5 days and 14 days, respectively. None of the cases make any difference in terms of the day of peak as compared to the case with no intervention. The fraction of infections that happen at the four big museums are slightly smaller, as expected.
In order to understand these outcomes, we calculate the number of contacts and duration per contact within and between these four subpopulation when museums are closed. We find that when the museums are closed, though the number of contacts within and between rt and tr subpopulations decreases, duration per contact in the population as a whole increases. This happens because people are assumed to move from one room (exhibition) to another at an interval of 5 to 15 minutes within the museums and hence the duration per contact within museums is less than at other locations. The increase in duration of contact appears to be enough to compensate for the decrease in number of contacts (infection rates are reported in the Supplementary Information ) and consequently, the number of infections is not significantly affected.
We also perform similar experiments in the absence of transients to see if closing museums helps if there are no transients visiting the city. The simulation results suggest that closing museums does not reduce number of infected individuals, even in the absence of the transients (Figures 4, 5 and 6; also see supplementary information ). To confirm our findings for the closing museums intervention, the contact rates and the average duration per contact are used to analytically study the spread of epidemic using the ODE model. Results show that there is no reduction in the final number of infected individuals comparing to the non-intervention scenario; see ( supplementary information ). Thus, the closing museums intervention does not reduce number of infected cases.
Healthy behavior intervention
Instead of closing locations where a large amount of mixing occurs, we can view them as places where we can promote healthy and cautious behaviors and hence reduce the number of infections that happen within those locations. Hence, we evaluate a scenario where people are encouraged to practice healthy behaviors, such as the use of hand sanitizers, at the four big museums. Multiple studies have shown that such non-pharmaceutical behavioral interventions can have a significant impact15.
As it is unclear that how much infectivity and susceptibility are reduced by the healthy behavior, we did a series of experiments assuming that the practice of healthy behavior reduces infectivity and susceptibility to 80%, 60%, 40% and 20% of their original values (effective only inside the four museums). We assume that 50% of the people going to these places practice healthy behavior. Figures 4, 5 and 6 show the box-plots comparing the fraction of residents infected at peak, the fraction of residents infected cumulatively over 120 days of simulation period and the day of peak. Simulations show that this intervention delays the peak of the epidemic by about 2 to 5 weeks. Under the least efficacious assumptions for healthy behavior (80% and 60%), it reduces the resident number of infections at peak by 6% and 14.6% respectively, as compared to the case when no intervention is applied. It also reduces the total number of residents infections over the period of 120 days by 3.6% to 9%, respectively. Improving efficacy further (40% and 20%) decreases the peak by 28.5% and 37.5% respectively. In these two cases, the cumulative number of infections over 120 days is reduced by 26.6% and 34.6%, respectively.
We also perform similar experiments to evaluate the effect of healthy behavior in the absence of transients (Figures 4, 5 and 6; also see supplementary information ). If efficacy of healthy behavior is 80% or 60%, the peak is delayed by 10 days or a month, respectively. The percentage reduction in the fraction of residents infected at peak and cumulatively over 120 days are similar to the results in the presence of transients. However, as more residents are infected when transients are considered, the actual benefit of the intervention is more (as the reduction in number of resident infection is more) in the presence of transients. If efficacy is further improved to 40% or 20%, the disease does not peak during the simulation period (120 days), which means peak is delayed by at least two months.
As healthy behavior interventions are assumed to be effective only inside the museums, we further divide each of the four subpopulations used for the ODE model into the people who go to the four museums and those who don't, resulting in six subpopulations. However, the subpopulation of residents who visit museums but only meet residents is very small and so it is ignored. The contact pattern among the subpopulations is as shown in Figure 11. Using the ODE model and the next generation method, we numerically evaluate the reproductive number for different compliance rates and reduced transmissibility values as shown in Figure 12. The reduction of reproductive number27 is nonlinearly proportional to the reduced transmissibility value. The nonlinearity is clearly observed for higher compliance rate. For compliance rate of 50%, when the transmissibility is reduced to 80% and 60% of its original value, the reproductive number is reduced by 9% and 18%, respectively. Significant reduction in the reproductive number is observed when the transmissibility is reduced to 40% and 20% of its original value. We also notice that the largest reduction of reproductive number is 58% for compliance rate of 100% and reduced transmissibility value of 0 inside the museums.
For healthy behavior interventions, resident and transient populations are further divided based on whether they visit one of four museums.
The Residents – Transients at museums subpopulation represents residents who visit the museums and meet both residents and transients. Similarly, the Transients – Residents at museums subpopulation represents transients who visit the museums and meet both transients and residents. These two subpopulations are denoted as rtm and trm and they have contacts inside the museums (red) and outside the museums (blue). The other three subpopulations (rrnm, rtnm and trnm) represent subpopulations of individuals who do not visit museums.
Discussion
Individual-based model reveals detailed structure of human location-based contacts among different subpopulations. Such detailed contact patterns can not be captured through classical models assuming homogeneous mixing among/within subpopulations. In summary, including the transient population makes a significant difference in epidemic estimation. However, a commonly recommended non-pharmaceutical intervention–social distancing–surprisingly does not show a statistically significant effect at reducing the outbreak. In this case, it seems that locations where a lot of mixing occurs are better thought of as presenting opportunities for reducing disease spread by promoting healthy behavior such as the use of hand sanitizers or covering cough. This intervention, under reasonable assumptions about its efficacy, shows a significant difference to the peak and the cumulative number of infections, as well as the day of the peak.
Results obtained from the ODE model are qualitatively in agreement with results obtained from the agent-based model. The epidemic spreads more when the transient population is introduced in the agent-based model. The same conclusion is obtained through the reproductive number that is found to be greater than 1 using the ODE model. For closing museums intervention, results obtained from both the agent-based model and the ODE model confirm that such an intervention does not significantly reduce the total number of infections. For healthy behavior intervention, both the agent-based model and the ODE model confirm the significant influence of promoting the usage of healthy behaviors at locations of high mixing help to reduce the total number of infected individuals. Therefore, we conclude that results obtained from both the agent-based model and the ODE model are consistent and in agreement.
Models like these can also be used for policy recommendations, for example to promote the use of hand sanitizers in museums. That in turn would offer the opportunity to conduct a field experiment to validate our model against actual epidemic and intervention data.
Limitations: The model we have constructed is as detailed and high-fidelity as we can make it, but it is important to note some limitations as well. First, while we model museums as locations of high mixing, these are not the only locations where high mixing between transients and residents may occur. Places like public transport (trains, train stations, airports) are also expected to have a similar influence on epidemics due to the high degree of mixing that happens at these locations. However, we do not expect that qualitative results will change if we include those locations. Second, we do not model the effects of transients bringing disease into the region. We have assumed that they are all susceptible when they arrive. We also do not model the possibility of outgoing infected transients infecting incoming transients or residents at the airports. Adding these factors would exacerbate the effects of transients on the epidemic in the region. Third, we do not distinguish between different mechanisms of transmission (direct, droplet, fomite). We have assumed that our “healthy behavior” intervention has an overall effect of reducing transmission by a certain fraction. In practice, depending on the behaviors promoted (use of hand sanitizer, covering coughs, etc.), the reduction in transmission would vary. Again, however, we expect that our qualitative results would hold.
Methods
Synthetic population
We generated an augmented synthetic population for the Washington DC Metro Area, which combines a previously generated resident population (the “base population” consisting of 4.13 million people) with a transient population (about 50000, 55% of which are tourists and the rest are business travelers). Each synthetic individual is assigned demographics (e.g., age, income) and a daily schedule of activities. Individuals are assigned activity schedules based on their demographics. A daily schedule of activities is written as a list of (activity type, start time, duration, activity location) tuples. Each activity location is subdivided into sublocations (similar to rooms within a building). A person is assumed to come in contact with all people present at the same sublocation at the same time, which thus induces a social contact network.
The methodology for generating the transient population broadly follows that for generating the base population. We first use demographic data to represent transient individuals and transient parties (groups). Each transient party is placed in a hotel which serves as their home for the period of the visit. Each transient individual is then assigned activities to perform during the day like staying in the hotel, visiting museums and other tourist destinations (or work activities, for business travelers), going to restaurants and various night life activities. Each activity is represented by the type of activity, the time each activity begins and ends and the location for the activity. A location is chosen for each activity based on the type of activity using Dun & Bradstreet data. The detailed process is described in Supplementary Information .
Simulation
We simulate a flu-like disease for Washington DC metro area using EpiSimdemics, an interaction based high performance computing simulation software for studying large scale epidemics16.
A 12-state Probabilistic Timed Transition System (PTTS) disease model, is a flu-specific model developed in Models of Infectious Disease Agent Study MIDAS in National Institutes of Health2 and it is used for the agent-based simulation. The PTTS represents the progression of health state of every susceptible individual in case of contracting the infection. A susceptible individual contracts the infection through infectious contacts with probability pi

where ξ is the set of infectivities of the infected individuals, αi is the susceptibility of individual i, p is defined as the probability of disease transmission from a completely infectious individual to a completely susceptible individual during one minute of contact4, T is the total duration of contacts and  is the number of infectious contacts with infectivity ξj. The disease model used is as shown in Figure 13.
is the number of infectious contacts with infectivity ξj. The disease model used is as shown in Figure 13.
Disease model used for simulation.
Each node represents a state and transition probabilities are as shown on the edges. Each node label consists of the state name, number of days for which an individual remains in this state and the probability of him infecting others. The histogram in the upper right corner shows the probability of being in the given state versus the number of days for symptom1, symptom2, symptom3 and asymptomatic states.
Differential equation based (SEIR) model
To compare simulation results with the differential equation based model (SEIR), the 12-state disease model shown in Figure 13 is collapsed into a 4-state SEIR model. Uninfected and recovered states in Figure 13 correspond to susceptible and recovered states in SEIR model respectively. Latent short, latent long and incubating states correspond to exposed state for SEIR model. A person is assumed to stay in the exposed state for approximately one day (weighted average of the number of days a person stays in latent short or latent long and incubating states). The remaining states in the 12-state model correspond to the infectious state in the SEIR model. A person is assumed to stay in the infectious state for 4.1 days (weighted average of the number of days a person stays in symptom1 circulating and symptom1, symptom2 circulating and symptom2, or symptom3 circulating and symptom3 states). In the ODE models, the infection rates are proportional to the average contact rates and the average duration per contact. The average contact rates and the average duration per contact among the populations are computed from the synthetic social network. Therefore, we emphasis that these computed values are used to set the parameters of the ODE models.
References
Molinari et al. The Annual Impact of Seasonal Influenza in the US: Measuring Disease Burden and Costs. Vaccine 25, 5086–5096 (2007).
Models of Infectious Disease Agent Study. http://www.nigms.nih.gov/Research/FeaturedPrograms/MIDAS/, 2013 September 1.
Barrett et al. Interactions among human behavior, social networks and societal infrastructures: A case study in computational epidemiology. Springer Verlag, 479507 (2009).
Barrett, C. et al. Modeling and simulation of large biological, information and socio-technical systems: An interaction-based approach. In Proceedings of Symposia in Applied Mathematics 64, Springer (2007).
Mossong, J. et al. Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases. PLoS Med 5, e74 (2008).
Marathe, A., Lewis, B., Chen, J. & Eubank, S. Sensitivity of Household Transmission to Household Contact Structure and Size. PLoS ONE 6, e22461 (2011).
Goldstein et al. Distribution of vaccine/antivirals and the “Least Spread Line” in a stratified population. J. Roy. Soc. Inter. 7, 755–764 (2010).
Fefferman, N. H. & Ng, K. L. How disease models in static networks can fail to approximate disease in dynamic networks. Phys. Rev. E. 76, 031919 (2007).
Ferguson, N. et al. Strategies for mitigating an influenza pandemic. Nature 442, 448–452 (2006).
Washington DC's Official Travel Website. http://washington.org, 2012 June 15.
Eubank, S. et al. Modelling disease outbreaks in realistic urban social networks. Nature 429, 180–184 (2004).
Heffernan, J., Smith, R. & Wahl, L. Perspectives on the basic reproductive ratio. J. Roy. Soc. Inter. 2, 281–293 (2005).
Driessche, P. & Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. J. Math. Bios. 2, 29–48 (2002).
Saenz, R. & Hethcote, H. Competing species models with an infectious disease. Math. Biosc. and Eng. 3, 219–235 (2006).
Aiello, A. E. et al. Research Findings from Nonpharmaceutical Intervention Studies for Pandemic Influenza and Current Gaps in the Research. Am. J. Infect. Control 38, 251–258 (2010).
Bisset, K., Feng, X., Marathe, M. & Yardi, S. Modeling interaction between individuals, social networks and public policy to support public health epidemiology. Proceedings of Winter Simulation Conference 2020–2031 (2009).
Anderson, R. M. & May, R. M. Infectious Diseases of Humans. (Oxford University Press, 1991).
Diekmann, O. & Heesterbeek, J. A. P. Mathematical Epidemiology of Infectious Diseases. (Chichester: John Wiley & Sons, Ltd., 2000).
Rvachev, L. A. & Longini Jr, I. M. A mathematical model for the global spread of influenza. Math. Biosci. 75, 3–22 (1985).
Hanski, I. & Ovaskainen, O. The metapopulation capacity of a fragmented landscape. Nature 404 (2000).
Diekmann, O., Heesterbeek, J. A. P. & Metz, J. A. J. On the definition and the computation of the basic reproduction ratio Ro in models for infectious diseases in heterogeneous populations. J.Math. Biol. 28 (1990).
Arino, J. & van den Driessche, P. The Basic Reproduction Number in a Multi-city Compartmental Epidemic Model. LNCIS. 294 (2003).
Colizza, V., Barrat, A., Barthélemy, M. & Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. Natl. Acad. Sci. 103 (2006).
Colizza, V., Pastor-Satorras, R. & Vespignani, A. Reaction diffusion processes and metapopulation models in heterogeneous networks. Nature Phys. 3 (2007).
Colizza, V., Barrat, A., Barthélemy, M., Valleron, A.-J. & Vespignani, A. Modeling the worldwide spread of pandemic inuenza: baseline case and containment interventions. PLoS Med. 4 (2007).
Fulford, G. R., Roberts, M. G. & Heesterbeek, J. A. P. The Metapopulation Dynamics of an Infectious Disease: Tuberculosis in Possums. Theor. Pop. Biol. 61 (2002).
Sahneh, F. D., Chowdhury, F. N. & Scoglio, C. M. On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading. Nature Sci. Rep. 2 (2012).
Acknowledgements
We thank our external collaborators and members of the Network Dynamics and Simulation Science Laboratory (NDSSL) for their suggestions and comments, especially Youngyun Chungbaek for help with the statistics. This work is supported in part by DTRA CNIMS Contract HDTRA1-11-D-0016-0001, NIH MIDAS Grant 2U01GM070694-09 and NSF HSD Grant SES-0729441.
Author information
Authors and Affiliations
Contributions
N.P., M.Y., S.S. & S.E. designed research. N.P., M.Y., S.S. & S.E. wrote the main manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information: Modeling the effect of transient populations on epidemics in Washington DC
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Parikh, N., Youssef, M., Swarup, S. et al. Modeling the effect of transient populations on epidemics in Washington DC. Sci Rep 3, 3152 (2013). https://doi.org/10.1038/srep03152
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03152
This article is cited by
-
A Mathematical Modeling Study: Assessing Impact of Mismatch Between Influenza Vaccine Strains and Circulating Strains in Hajj
Bulletin of Mathematical Biology (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.








 , where the disease spreads in both populations. At equilibrium, residents are either susceptible or recovered and transients are susceptible because infected transients leave the city and are replaced by susceptible transients, while the transient reproductive number is below 1.
, where the disease spreads in both populations. At equilibrium, residents are either susceptible or recovered and transients are susceptible because infected transients leave the city and are replaced by susceptible transients, while the transient reproductive number is below 1.  , where the disease persists in the transient population. Due to the assumption that every resident has contacts with transients, all residents eventually contract the infection and recover. However, the synthetic social network reveals the fact that not all residents meet transients. Therefore, a more detailed model is introduced to distinguish between residents who have contacts with residents only and residents who have contacts with residents and transients.
, where the disease persists in the transient population. Due to the assumption that every resident has contacts with transients, all residents eventually contract the infection and recover. However, the synthetic social network reveals the fact that not all residents meet transients. Therefore, a more detailed model is introduced to distinguish between residents who have contacts with residents only and residents who have contacts with residents and transients. 





