Abstract
In most professional sports, playing field structure is kept neutral so that scoring imbalances may be attributed to differences in team skill. It thus remains unknown what impact environmental heterogeneities can have on scoring dynamics or competitive advantages. Applying a novel generative model of scoring dynamics to roughly 10 million team competitions drawn from an online game, we quantify the relationship between the structure within a competition and its scoring dynamics, while controlling the impact of chance. Despite wide structural variations, we observe a common three-phase pattern in the tempo of events. Tempo and balance are highly predictable from a competition's structural features alone and teams exploit environmental heterogeneities for sustained competitive advantage. Surprisingly, the most balanced competitions are associated with specific environmental heterogeneities, not from equally skilled teams. These results shed new light on the design principles of balanced competition, and illustrate the potential of online game data for investigating social dynamics and competition.
Similar content being viewed by others
Introduction
Competition between groups is a ubiquitous feature of human social systems. Classic game theory, which models competition outcomes from strategic decisions within relatively well-defined choices, has yielded many insights into the principles of competition1. However, many real-world competitions are better represented as dynamical systems, in which computationally limited players imperfectly navigate many possible actions with uncertain payoffs2, and traditional models say relatively little about the dynamics within these systems. The empirical study of dynamical competitions promises to shed new light on fundamental questions about competition, and team sports provide a rich and relatively controlled domain through which to do so3,4.
A distinguishing feature of most team sport competitions is their structurally homogeneous or “level” playing field, which allows differences in team scores to be attributed to one team being relatively more skilled than another, or, if the difference is small, to chance events5,6. This design choice eliminates the impact of structural heterogeneities, like an irregular playing field, variations in rules, or differences in within-competition resources, on a competition's internal dynamics. Models of economic competition suggest that such heterogeneities should produce structural competitive advantages7, allowing a team to perform above its skill level by exploiting these environmental irregularities. These models, however, provide little guidance about the relative importance of different heterogeneities and say little about the relative impact of skill (or other team-endogenous variables), structure (or other team-exogenous variables), and chance on competition outcomes.
In fact, it is not generally known how to disentangle the roles these factors play in determining competition outcomes, and their relative importance remains a highly controversial topic, both in sports8 and in other types of social competition7,9,10. A better understanding of these issues would inform our general understanding of the principles of competition in human social systems and the design of novel competitive environments11,12. To the extent that underlying commonalities exist, progress on these topics may also shed new light on competition dynamics in other domains, such as ecology and evolutionary biology13, political conflict1 and economics14.
A novel approach to investigate these questions lays in online games, which are proving increasingly useful in investigating a wide variety of complex questions about human social dynamics17,28,29. In general, online games encompass a broad and growing variety of relatively controlled competitions, played by large and demographically diverse populations15, and, critically, producing large quantities of detailed observational data by which to quantify subtle patterns and test complex hypotheses.
Here, we study a unique data set drawn from the popular online game Halo (see SI Appendix ), a kind of virtual team combat, which contains nearly 1 billion scoring events across roughly 10 million diversely structured team competitions. Although Halo is a particular online game, it exhibits several features that make it a model system for studying questions about human competition dynamics. In particular, each competition is essentially independent, with team memberships being substantially randomized across competitions, and with no resources carried between competitions. These features thus mitigate the confounding effects of cross-competition correlations present in professional sports, e.g., fixed team rosters and differences in team budgets, and provides a randomized control for studying how structural variations shape competition dynamics and outcomes.
To quantify the impact of structure on dynamics, we partition these competitions according to their particular environmental structure, competition rules, resource quality and difference in team skill, and then characterize their scoring dynamics via a probabilistic model. The resulting model parameters provide a compact representation of that group of competitions' internal dynamics, which serve as targets to be explained by variation in structural features.
Despite wide variation, structure has a modest impact on the tempo of events, but a large impact on the scoring balance, i.e., the difference in team scores. Additionally, the rate of scoring events over time exhibits the same three-phase pattern observed in professional sports16. Overall, structural features alone are highly predictive of overall competition tempo, the range of competitive scoring advantages, and ultimate predictability of the competition's outcome. Like business firms competing in the marketplace7, teams appear to exploit environmental and resource heterogeneities to achieve sustained competitive advantages. However, contrary to the pattern of professional sports, the most balanced competitions—those with narrow margins of victory—arise from specific environmental heterogeneities, not from equally skilled teams competing in homogeneous environments. These results illustrate the rich potential of online game data for investigating social dynamics and competition17, clarify the role of chance when teams are well matched, and point to specific design principles for balanced competitions.
Results
Quantifying competition dynamics
We first introduce the notion of an “ideal” competition, in which perfectly matched teams play on a level field with no exploitable features. Such a competition's outcome is thus determined solely by the occurrence and accumulation of chance events, e.g., accidents, miscalculations, and events outside direct control. In this way, perfect performance by equally skilled teams will produce purely stochastic dynamics.
These dynamics can be described by a particularly simple stochastic process18. Scoring events occur infrequently and independently, and their pattern follows a Poisson process with rate λ0—a common assumption in quantitative analysis and modeling of professional sports16,19,20. Given a scoring event occurs, a fair coin determines which team accrues points from it. The difference in scores between teams thus follows an unbiased random walk (Fig. 1a), and scoring overall follows an equiprobable or balanced Bernoulli scheme.
(a) Scoring trajectories for ideal competitions. (b) Scoring trajectories for non-ideal competitions where β = 29.5, the system's global average. (c) Distribution of final score differences for ideal and non-ideal competitions. When competitions are ideal, scoring trajectories remain near 0 and variability in final score differences is relatively small. When competitions deviate from ideal, scoring trajectories stray from 0 and variability in final score differences increases.
Real competitions, with heterogeneous structure or skill differences, will deviate from this ideal, and it is useful to measure how far from the ideal a particular real competition lays. We capture these deviations through a generalized model, which may be fitted directly to scoring data and whose parameters quantify the size and character of the non-ideal patterns. We then investigate the extent to which the observed non-ideal patterns can be predicted from variation in competition structure.
We assume a competition between teams r and b, and we let sr(t) denote team r's cumulative score at an intermediate time t < T. The probability that r's score increases at time t is given by the joint probability of a scoring event occurring at t and of r scoring it. Letting these probabilities be independent yields

where θ parameterizes the non-ideal patterns.
Scoring events occur infrequently and independently, and are now produced by a simple non-stationary point process, in which the arrival of events varies linearly with time:

The base or background rate is given by λ0 and α parameterizes the non-stationarity, e.g., increasing (α > 0) or decreasing (α < 0) tempo. When α = 0, we recover the ideal case of a Poisson process with rate λ0.
The score of a team follows a general Bernoulli process. Given a scoring event, points are awarded to team r with some probability that is fixed for this competition, but which may vary between competitions

and otherwise, they are awarded to team b. This scoring bias c is a probabilistic measure of r's competitive advantage over b, e.g., from a difference in skill or from exploitable features of the competition. When c = 1/2, we recover the ideal case of a balanced Bernoulli process, while deviations produce the more lopsided trajectories associated with non-ideal dynamics (see Fig. 1a,b).
Across competitions with the same structure, different pairs of teams will exhibit different competitive advantages. Thus, the natural explanatory target is the distribution of the scoring imbalances Pr(c), whose natural form is a symmetric Beta distribution21 (see SI Appendix ), the conjugate prior for the Bernoulli process. The result is a one-parameter model that quantifies the overall variability in competitive advantages across a set of competitions. The ideal case of perfectly matched teams and scoring differences due only to chance events occurs at c = 1/2, which is recovered in the limit of β → ∞ (Fig. 1a,c). Smaller values of β produce scoring trajectories that result in larger variance in final score (Fig. 1b,c).
We supplement this parametric approach with a non-parametric measure of non-ideal behavior: the predicability of the winner from a partially unfolded competition. Having observed the first k scoring events, predicting the winning team is a kind of classification task, which we formalize as a Markov chain on the sequence of team scores (see SI Appendix ). For two-team competitions, the probability that team r wins, given current scores sr and sb, is

where  estimates r's competitive advantage. After each event, the classifier predicts as the winner the team with the greatest estimated odds-to-win, and its accuracy is measured by the AUC statistic22, the probability of choosing the correct winning team.
estimates r's competitive advantage. After each event, the classifier predicts as the winner the team with the greatest estimated odds-to-win, and its accuracy is measured by the AUC statistic22, the probability of choosing the correct winning team.
The AUC versus k provides complete information about a competition's predictability but is not amenable to our subsequent analysis. We instead use a point measure ρ, defined as the ratio of the Markov classifier's AUC to that of an ideal competition (c = 1/2), when 20% of the competition has unfolded. A value of ρ > 1 indicates that the competition outcomes are more predictable than in the ideal case.
Competition data
Our data are drawn from the popular online game Halo: Reach, and span nearly 1 billion scoring events across roughly 10 million diversely structured team competitions. These competitions are divided into 125 types according to 35 structural features defining the spatial environmental, competition rules, resource quality, and whether teams had roughly equal skill (see SI Appendix ).
Halo competitions are a kind of real-time virtual combat. Human players guide their avatars through an arena containing complex terrain, coordinate actions with teammates through visual and audio signals, and encounter opponents. A scoring event occurs when one avatar eliminates another, and this event increments the former's team score. After a short delay, the latter is returned to the competition at another arena location. Competitions end either when a fixed time limit is reached (typically 10 minutes) or when one team's score reaches some threshold (typically 50).
Only individual player skill persists across competitions. Temporary resources, whose control may yield a competitive advantage, are acquirable within a competition, e.g., highly defensible positions, high quality avatar items, and tactical information. Team membership is also temporary, being substantially randomized across competitions by the online system. These features make Halo competitions a model system for investigating the impact of structural heterogeneities on competition dynamics by creating a kind of randomized control that eliminates the impact of cross-competition variables, e.g., fixed team rosters or team budgets, that exist in professional sports. That is, Halo competitions may be treated as roughly iid draws from an underlying stochastic process, a feature that mitigates confounding effects in characterizing the importance of structural variations.
From the scoring events within a given type of competition, we estimate both model parameters and the outcome predictability (see
SI Appendix
). This produces a set of coordinates ( ,
,  ,
,  ,
,  ) and provides a compact and interpretable summary of that competition type's scoring dynamics and variability. Letting
) and provides a compact and interpretable summary of that competition type's scoring dynamics and variability. Letting  denote the structural features of a given competition type, explaining variation across the estimated coordinates from variation in
denote the structural features of a given competition type, explaining variation across the estimated coordinates from variation in  will reveal the impact of structural features on competition dynamics, if any. Although here
will reveal the impact of structural features on competition dynamics, if any. Although here  is a set of binary variables indicating the presence or absence of particular structural features, this approach is entirely general and could be applied to features with real- or integer-values.
is a set of binary variables indicating the presence or absence of particular structural features, this approach is entirely general and could be applied to features with real- or integer-values.
The determinants of balance β, which quantifies the strength and distribution of competitive advantages, are of particular interest. Players may prefer more balance because it offers a fair chance at winning. Or, they may prefer less balance because it offers greater reward for the risk. In these competitions, we find that greater balance correlates with a lower probability that at least one player will prematurely leave the field of play (r2 = 0.43, see SI Appendix ), typically a voluntary action. Thus, players exhibit a moderate but real preference for more balanced, i.e., more ideal, competitions, whose outcomes are less predictable, whose final score differences are smaller, and whose dynamics are closer to those of a simple stochastic process.
Patterns in tempo and score dynamics
We first verify that our generative model effectively captures the true scoring dynamics of these competitions and whether they exhibit patterns similar to those of professional sports.
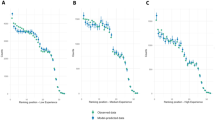
Across all competition types, we find a consistent three-phase non-stationary pattern in the tempo of scoring events, i.e., the probability of a scoring event as a function of time elapsed or time remaining. Specifically, we find an early phase of little or uneven activity, a protracted middle phase of slow and steadily increasing activity, and an end phase of either slightly decreased or markedly increased activity (Fig. 2a–c). This same three-phase pattern is also observed in professional sports (see SI Appendix , Fig. S5), in support of our use of an online game as a model system for studying competition dynamics.
The early- and end-phase patterns are caused by boundary effects in the length of competition, and are also observed in professional sports16. Early in a competition, players require some time to move from their initial set positions to their first scoring opportunities, which suppresses the tempo of events relative to the ideal case. Although the shape of this early phase varies moderately by competition type (Fig. 2a), after 20–30 seconds these variations largely disappear and the tempo transitions into the more stable middle phase.
Similarly, near a competition's end, the impending cessation of scoring opportunities encourages different strategic choices1 than in the early or middle phases. Here, we observe either slightly decreased or strongly increased tempo (Fig. 2c), depending on whether the competition type's particular rules provide an incentive for risk taking in the final seconds. When the incentive is present, the tempo increases dramatically just before the competition ends, as players take greater risks for the win—a pattern also observed in professional sports16,19. When the incentive is absent, players instead adopt defensive positions to deny the opposing team additional points, leading to decreased scoring rates—a pattern not typically observed in sports (see SI Appendix , Fig. S5).
In contrast, the middle phase's tempo exhibits a roughly linear increase over time (Fig. 2b), which agrees with our generative model for event timing. To estimate our tempo model parameters, we eliminate the boundary effects by focusing on events in this phase alone (see SI Appendix ). Across competition types, both the base tempo and the acceleration vary widely: base rates by up to a factor of two and tempo by 5–20% over the phase. Within-competition learning is one plausible explanation for this increase23, e.g., through trial and error, teams may learn how and where to produce scoring events, which would progressively reduce the time spent searching for new scoring opportunities and thereby increase the tempo of events.
To understand the variation in the accumulation of points, we examine the distributions of scoring biases across competition types. For a particular competition, the scoring bias is estimated as the fraction of points held by an arbitrarily labeled team r. We find that all competition types exhibit moderately non-ideal variations in scoring biases (Fig. 3), i.e., they are consistently dispersed from the ideal case of c = 1/2. As with the competition tempo in the middle phase, the degree of dispersion varies substantially across competition types, suggesting a significant role for structural variables.
As a further test of our generative model's quality at modeling dynamics within these competitions, we estimate λ0, α and β from the entire data set, draw many synthetic competitions from the fitted model, and consider whether the simulated scoring dynamics are similar to those in the empirical data. The results indicate that the simulated competitions match the observed sequences on multiple scoring and timing statistics unrelated to parameter estimation (see SI Appendix ). This quantitative agreement indicates that our model successfully captures the important dynamical features of our competitions.
How structure shapes dynamics
We now investigate four specific types of structure and their impact on the estimated competition dynamics. These analysis are intended to shed light on how specific structures may shape dynamics, and will aid the interpretation of our systematic analysis below.
Team skill differences
When assigning individuals to a new competition instance, the online system uses a matchmaking algorithm to substantially randomize team composition. This algorithm operates in two modes. For players who have completed a moderate number of competitions, it adjusts team memberships so that the skill differences between teams are small. These precise estimates, which are not variables in the data, are derived from a Bayesian generalization of the popular Elo rating system of individual player skill, known as TrueSkill6. TrueSkill estimates “skill”, which is not a simple or arbitrary measure like action rate, but rather related to the probability of winning a match, by integrating over many types of actions. Otherwise, teams are assembled without regard to player skill and skill differences between teams are large. We examine the differences in our model parameters for all competitions constructed under each of the two modes.
Differences in skill have a substantial impact on competition balance, as we might expect. However, they have little impact on competition tempo (Table I, Fig. S4a). When teams have roughly equal skill, scoring is more balanced than when the equal-skill control is absent (β = 45.9 ± 0.35 versus 20.9 ± 0.22). This difference implies that well-matched teams produce substantially more ideal competitions, have smaller competitive advantages, and exhibit overall dynamics that are closer to those produced by a fair coin. In effect, reducing the difference in team skill serves to amplify the importance of chance events, i.e., accidents and miscalculations.
Physical environment
The arenas for these competitions are typically complex virtual terrains, and may contain large outdoor spaces, complicated indoor corridor systems, buildings with multiple levels, defensible positions, high ground, etc. We compare model parameters for all competitions taking place within two structurally distinct environments: one is largely neutral, exhibiting strong spatial symmetries and few features like defensible locations that might offer tactical advantage, while the other is strongly irregular, with an asymmetric and strongly vertical spatial structure, truncated sight lines, and at least one defensible location.
Overall, the more symmetric environment produces substantially more balanced outcomes and higher scoring rates than the irregular one. In fact, the observed difference in balance parameters is roughly as large as the difference induced by the equal-skill criterion (Table I, Fig. S4b). This suggests that increasing the homogeneity of the competitive environment, e.g., introducing symmetries, removing defensible positions, etc., serves to limit environmental opportunities for competitive advantage. Much like eliminating differences in skill, simpler environments effectively amplify the importance of chance events, making competition scoring more ideal.
Scoring difficulty
Few studies have examined the difference in competition dynamics caused by variations in the rules of the competition. Our data include several variations of this kind, and we examine one particular variant to shed light on how small changes in rules may impact competition dynamics. A popular group of competition types alters the standard scoring rules by reducing the threshold required to eliminate an opposing avatar and by slightly limiting each player's visual field. These changes make scoring opportunities easier to exploit, and we compare the estimated model parameters for all competitions of the standard and easy scoring types.
Lowering the threshold for scoring has a substantial impact on competition dynamics (Table I, Fig. S4c), with easier scoring rules producing less balanced outcomes. The size of this difference is nearly half as large as the impact of the equal-skill criterion. Additionally, the lower threshold decreases the base scoring rate by 15% but increases the acceleration by roughly 8% over those of standard competitions. The implication is that lowering the barrier to scoring skews the playing field, allowing skilled players to exploit either their skill-based competitive advantage or other structurally-derived advantages.
Resource quality
Each competition has a fixed a set of acquirable resources, which players use to score points. Each resource belongs to one of two classes, which we label “versatile” and “limited.” Versatile resources are generally of higher quality and are more effective for scoring points. When resources of both classes are present in a competition, 80% of scoring events are associated with the versatile class, illustrating a strong player preference for more effective tools. To clearly separate their effects, we examine competitions with either only versatile- or only limited-class resources.
Limited-class competitions produced moderately higher base and acceleration rates than versatile-class competitions, indicating an overall faster tempo. Furthermore, competitions with only limited-class resources produce substantially more balanced scoring outcomes (β = 41.7 ± 1.04 versus 20.2 ± 0.52; Table I, Fig. S4d), a difference as large as that of the equal-skill criterion. Just as environmental structures can be exploited for competitive advantages, differences in the quality of acquirable resources also represent exploitable structural heterogeneities, and limiting such variations can effectively level a playing field to produce more ideal dynamics.
Structural determinants of competitive dynamics
Each competition type defines a point on a (λ0, α, β, ρ)-manifold, and the distribution of these points describes the observed variability in competition dynamics. We now consider the degree to which a competition's position in this coordinate space is predictable from its structural features alone.
The joint distribution of the model timing parameters λ0 and α is broadly distributed and shows little internal structure (Fig. 4). The typical scoring base rate is roughly one event per 7.5 seconds, with variations of 2.5 s in either direction. Additionally, nearly all competitions types show modest acceleration rates, with an increase of 10–12% over the middle-phase of competition being common. Were timing parameters anti-correlated, with lower base rates correlating with higher acceleration, we would have some evidence that teams were learning how to predict the likely locations of new scoring opportunities. However, the lack of correlation, in either direction, suggests that teams do not in general improve their efficiency by learning within a competition.
The estimated balance parameters β are also broadly distributed, indicating a wide range of competitive advantages. The typical competition type has β between 20 and 30, but some have values as large as 50 or as small as 10 (Fig. 5). We observe a strong negative correlation between scoring balance β and the predictability ρ of a competition's winner, as expected under our generative model. However, the relationship between balance and predictability is not simple, and outcome predictability varies considerably in the very low β regime. Understanding the mechanism driving this variability is left for future work.
Predicting dynamics from structure
The extent to which a competition's dynamical variables (λ0, α, β, ρ) are predictable from its structural variables  provides a direct measure of how competition structure shapes dynamics. Thirty-five structural features, divided into resources (R), environment (E), team skill (S), and rules (P) categories, were used to identify 125 distinct types of competition. Regressing these structural features onto the estimated model parameters quantifies the overall predictability of dynamics from structure, and the resulting coefficients provide additional insights into the relative importance of specific factors.
provides a direct measure of how competition structure shapes dynamics. Thirty-five structural features, divided into resources (R), environment (E), team skill (S), and rules (P) categories, were used to identify 125 distinct types of competition. Regressing these structural features onto the estimated model parameters quantifies the overall predictability of dynamics from structure, and the resulting coefficients provide additional insights into the relative importance of specific factors.
Overall, competition dynamics are highly predictable from structure alone (Table II), with structural variables explaining 65–96% of the variance in individual dynamical parameters. Because the coverage across our feature space is sparse, we performed three additional tests to determine the robustness of our results. Both multiple and stepwise regressions produce models of nearly equal quality and assign features nearly the same relative importances. Randomizing the association of structural and dynamical variables yields non-significant correlations (see SI Appendix ), indicating our results are reliable. These results imply a very strong role for structural variables in shaping the dynamics of competitions.
 ,
,  and
and  of standard-type competitions from structural features alone, and the corresponding fraction of variance explained r2. Here, we show only the statistically significant features (
of standard-type competitions from structural features alone, and the corresponding fraction of variance explained r2. Here, we show only the statistically significant features ( , t-test); Table S6 provides the full results
, t-test); Table S6 provides the full resultsStructural variables have the largest impact on base rate λ0 (r2 = 0.96), with features describing neutral or homogeneous environments playing the dominant role in setting its value. The particular pattern observed can be explained by considering the “encounter rate” between scoring opportunities and competitors. Here, an encounter requires two individuals to locate and engage each other. Large, open and outdoor environments tend to be more neutral, and thus generate these encounters more often than irregular ones. While indoor terrains are spatially complex, but tend to be smaller, which should also increase the encounter rate. In agreement with this interpretation, we note that in team sports, scoring rates are highest on small playing fields, e.g., basketball and hockey, where encounter rates with scoring opportunities are high, and lowest on large playing fields, e.g., soccer and American football.
Although resources that allow engagement at larger distances should increase the base rate by effectively shrinking the size of the arena, medium- and long-range resources in fact decrease it, perhaps because players assume overly defensive playing styles in response. Finally, more equally matched and more skilled teams seems likely to increase the rate because players are more familiar with the environments, resources and tactics. However, we find that more equal skill raises the rate only marginally, and is between 4–16 times less important, in absolute value, than any other statistically significant feature.
The scoring acceleration rate α is moderately well predicted by structure (r2 = 0.65), although only two features are significant and both of which correlate with less acceleration, i.e., more ideal competitions, and substantial variation remains unexplained by any of our features. In contrast to the results for the other three estimated parameters, environmental variables play no role in increasing or decreasing the acceleration of scoring events. Although having equally-skilled teams correlates with more ideal competitions (less acceleration), it is seven times less important than teams having access to long-range resources. If such resources effectively shrink the size of the arena, scoring opportunities should be easier to locate and exploit. However, the absence of environmental variables correlated with small arena sizes, e.g., indoor terrain, suggests a more complicated mechanism. The unexplained variation may be attributable to learning effects, i.e., identifying and adapting to the opposing team's tactics, which are endogenous variables not represented in our set of competition features.
The scoring balance β, which measures the variance in observed competitive advantages, is highly predictable from structure (r2 = 0.93, regression on log β), as is the relative outcome predictability ρ (r2 = 0.89). In contrast with the tempo parameters, resource variables play no systematic role in either increasing or decreasing balance. Having well-matched teams does improve balance, as we would expect, but the magnitude of its contribution is surprisingly small. Instead, we find that specific environmental heterogeneities have a much larger balancing effect (0.36–1.25 times larger) than the skill variable. Well-balanced scoring typically appears in large, open or outdoor environments, a situation similar to the kind of level playing fields seen in professional team sports.
Our recovery of this intuitive correlation serves as a useful sanity check on the overall analysis, and supports the conventional wisdom that literally leveling the playing field improves the balance of competitions. Counter-intuitively, however, and in contrast with that conventional wisdom, the single most important feature, by a factor of two, for producing balanced competitions is the opposite of a level playing field, i.e., indoor terrain like rooms and corridors. One explanation for this pattern is that large amounts of spatial heterogeneity effectively handicap all competitors, regardless of skill, by limiting their ability to observe and anticipate nearby threats or opportunities. These results suggest that both extremely simple and extremely complex environments provide the fewest exploitable opportunities for sustained competitive advantage, while the middle ground—moderately complex environments—provides the most. The result is that both types of environments mitigate other sources of competitive advantages, including those derived from greater skill or strategic locations, moving scoring dynamics closer to the ideal.
In contrast, the most imbalanced and predictable competitions are those with controllable or strategically valuable environmental features like high ground or defensible positions. For setting the values of β and ρ, such features are at least as important, but opposite in sign, to having teams of equal skill. These strategically important environmental features can thus effectively upset the competitive balance produced by well-matched teams by providing one team with a sustained competitive advantage throughout the competition.
Surprisingly, variations in competition rules, including reduced spatial awareness, weakened defensive capabilities, or a lower threshold for scoring, were not statistically significant predictors. None of these features produced a measurable impact on the tempo or balance of scoring within competitions, once the effects of other features were taken into account.
Discussion
Although professional sports are often considered models of team competition16,19,20,24,25, their limited structural variation provides few opportunities for understanding how competition structure can shape competition dynamics. Our results shed new light on these and other fundamental questions about human social dynamics and competition.
In particular, heterogeneities in the spatial environment, available resources, competition rules, and team skill exert a strong influence on the balance and tempo of scoring dynamics within a competition. For the virtual team-combat simulation studied here, spatial structure plays the most important role in producing or eliminating competitive advantages, with skill and resource differences assuming supporting roles. Much like business firms exploiting heterogeneous and scarce resources, e.g., prime real estate, zoning permits, patents, etc., for sustained competitive advantage in the marketplace7,30, teams in our model system leverage environmental and resource heterogeneities, like high ground and defensible positions, toward the same ends. The modest role we observe for skill, after controlling for the impact of environmental variables and chance, suggests a larger importance for exogenous variables in economic competitions than has previously been appreciated7.
But unlike the pattern of either business firms or professional sports teams, some heterogeneities—in our case complex spatial environments—can effectively neutralize competitive advantages normally derived from exploitable structural features. When these “leveling” features are present, scoring outcomes are substantially more balanced than when they are absent, and this leveling effect is stronger than the one produced by having equally skilled teams. Although the precise mechanisms of these leveling effects remain unknown, their existence implies that competitive advantages are derived from specific mechanisms whose effects can be neutralized by other mechanisms. A better understanding of them could be derived from controlled experiments using designed online games, and may facilitate the design of inhomogeneous competitive environments that nevertheless exhibit the balanced dynamics that homogeneous environments produce.
Otherwise, the most ideal competitions occur in large neutral spaces between well-matched teams. Thus, it seems no accident that professional team sports are often played in precisely this type of environment: absent spatial or resource heterogeneity, competition between skilled teams is significantly more ideal. Combining this result and the previous one implies a general U-shaped dependency between competition balance and environmental complexity. Both extremely simple and extremely complex environments provide the fewest exploitable opportunities for sustained competitive advantage, while the most opportunities and the least balance appear in the middle ground, with moderately complex environments.
The close agreement between our generative model and the observed competition dynamics in our model system implies that the more balanced a competition, the more effectively it may be described as a purely random process, not despite but in fact because of the significant strategic and tactical effort behind individual events. In effect, as a competition becomes more ideal, chance events like miscalculations and accidents play a greater role in determining the final outcome. We note, however, that replacing the underlying competition mechanics by actual coin flipping seems unlikely to produce the same level or type of engagement among players and spectators.
The three-phase pattern in the tempo of events in our model system is strikingly similar to the pattern observed in professional team sports. Yet the underlying structures of most professional sports and our model system—a team combat simulation—could hardly be more different. In the former, goals have fixed locations, the environment and within-competition resources are homogeneous, and teams are highly trained and persistent. In the latter, goals are highly mobile, the environment and within-competition resources are heterogeneous, and teams are largely non-persistent. The existence of a common dynamical pattern despite such differences suggests that it may be a universal feature of team competitions. The elucidation of its origin is an important open question.
Finally, we omitted explicit roles for within-team variables like team composition26, coordination27, and player characteristics. Their impact is implicit within the estimated model parameters, whose variation is well explained by structural variables alone. This particular result is likely supported by the substantial randomization in team membership across our competitions, which serves to mitigate any significant differences in team composition. Player and team characteristics likely play a more significant role in determining the dynamics in competitions with persistent teams or homogeneous environments, as in professional sports. A broad study of within-competition dynamics across fundamentally different types of competition may shed complementary light on the origin of competitive advantages, the mechanisms by which specific features promote or discourage balanced outcomes, and the fundamental laws of competitive dynamics, if any.
Methods
In this section, we provide a broad overview of the computational and statistical methods we employed in this research. For a detailed explanation of what follows, please refer to the SI Appendix . Additionally, please see the SI Appendix for a detailed description of the data.
Model parameter estimation and goodness of fit
We estimate the parameters of our model of competition by directly maximizing the model's log-likelihood functions. The likelihood function which quantifies the probability of observing a series of scoring events is defined as,

where {ti} denote the observed times of these events, and {uj} the times at which no event was observed. For a complete derivation of the likelihood function, see the SI Appendix .
Similarly, we estimate the balance of competition, β, by directly maximizing its log-likelihood function, which is defined as,

where  and
and  are final scores of teams r and b in competition k. For details and additional checks of model robustness, see the
SI Appendix
.
are final scores of teams r and b in competition k. For details and additional checks of model robustness, see the
SI Appendix
.
To test the plausibility of our generative model, we compare simulated competitions against the empirical data along specific statistical measures. The simulation is parametric and uses the estimated parameters from our generative model to define the corresponding probability distributions in the simulator. A close match between the synthetic scoring dynamics and the empirical data along multiple statistical measure is evidence that our generative model accurately captures the basic features of these competitions. For details of the simulation framework and statistical measures, see the SI Appendix .
Multivariate regression analysis
To predict a competition's dynamical parameters, (λ0, α, β, ρ), from environmental structural features,  , we conduct a multivariate regression analysis. To test the robustness of our results against spurious correlation, due to the high-dimensionality of our data, we conduct three additional analyses. First, we study co-linearity between dependent variables by conducting a MANOVA. Second, we perform stepwise AIC feature selection to choose an optimal subset of features. Third, we perform a randomization test by randomly permuting dependent variables across features and repeating the original regression analysis. Our model is robust to these tests. For details of each test's procedure as well the corresponding results, see the
SI Appendix
.
, we conduct a multivariate regression analysis. To test the robustness of our results against spurious correlation, due to the high-dimensionality of our data, we conduct three additional analyses. First, we study co-linearity between dependent variables by conducting a MANOVA. Second, we perform stepwise AIC feature selection to choose an optimal subset of features. Third, we perform a randomization test by randomly permuting dependent variables across features and repeating the original regression analysis. Our model is robust to these tests. For details of each test's procedure as well the corresponding results, see the
SI Appendix
.
References
Myerson, R. B. Game Theory: Analysis of Conflict (Harvard University Press, Cambridge MA). (1997).
Galla, T. & Farmer, J. D. Complex dynamics in learning complicated games. Proc. Natl. Acad. Sci. (USA) 110, 1232–1236 (2013).
Reed, D. & Hughes, M. An exploration of team sport as a dynamical system. J. Performance Analysis in Sport 6, 114–125 (2006).
Jéro·me Bourbousson, C. S. T. M. Space-time coordination dynamics in basketball: Part 2. The interaction between the two teams. J. Spts. Sci. 28, 349–358 (2012).
Denrell, J. Random walks and sustained competitive advantage. Mgmt. Sci. 50, 922–934 (2004).
Herbrich, R., Minka, T. & Graepel, T. TrueSkill(tm): A Bayesian skill rating system. Adv. Neur. Inf. Proc. Sys. 20, 569–576 (2007).
Barney, J. Firm resources and sustained competitive advantage. J. Management 17, 99–120 (1991).
Ben-Naim, E., Hengartner, N., Redner, S. & Vazquez, F. Randomness in competitions. J. of Statistical Physics 151, 458–474 (2013).
Salganik, M. J., Dodds, P. S. & Watts, D. J. Experimental study of inequality and unpredictability in an artificial cultural market. Science 311, 854–856 (2006).
Denrell, J. & Liu, C. Top performers are not the most impressive when extreme performance indicates unreliability. Proc. Natl. Acad. Sci. (USA) 109, 9331–9336 (2012).
Michael, D. R. & Chen, S. L. Serious Games: Games That Educate, Train, and Inform (Muska and Lipman). (2005).
Nisan, N., Roughgarden, T., Tardos, E. & Vazirani, V. V. Algorithmic Game Theory (Cambridge University Press). (2007).
Boucher, D. H. in The Biology of Mutualism: Ecology and Evolution, ed Boucher, D. H. (Oxford University Press), pp 1–27 (1985).
Bowles, S. Microeconomics: Behavior, Institutions, and Evolution (Princeton University Press). (2006).
Entertainment Software Association Essential Facts about the Computer and Video Game Industry. http://bit.ly/kLHJ2Q, (access date February, 2012) (2011).
Gabel, A. & Redner, S. Random walk picture of basketball scoring. J. Quant. Analysis in Sports 8, Manuscript 1416 (2012).
Szell, M., Lambiotte, R. & Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. (USA) 107, 13636–13641 (2010).
Brzezniak, Z. & Zastawniak, T. Basic Stochastic Processes (Springer, Berlin). (2000).
Thomas, A. Inter-arrival times of goals in ice hockey. J. Quant. Analysis in Sports 3, (2007).
Heuer, A. & Rubner, O. How Does the Past of a Soccer Match Influence Its Future? Concepts and Statistical Analysis. PLoS ONE 7, e47678 (2012).
Bishop, C. M. Pattern Recognition and Machine Learning (Springer). (2006).
Bradley, A. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pat. Rec. 30, 1145–1159 (1997).
Thompson, P. in Handbook of Economics of Technical Change, eds Hall, B. & Rosenberg, N. (Elsevier/North-Holland), pp 429–476 (2010).
Sire, C. & Redner, S. Understanding baseball team standings and streaks. Eur. Phys. J. B 67, 473–481 (2009).
Ben-Naim, E., Vazquez, F. & Redner, S. What is the most competitive sport? J. Kor. Phys. Soc. 50, 124 (2007).
Guimerà, R., Uzzi, B., Spiro, J. & Amaral, L. A. N. Team assembly mechanisms determine collaboration network structure and team performance. Sci. 308, 697–702 (2005).
Mason, W. & Clauset, A. Friends FTW! Friendship and competition in Halo: Reach. 16th ACM Conf. on Comp. Supp. Coop. Wrk. and Soc. Comp. (2013).
Ahmad, M. A., Keegan, B., Williams, D., Srivastava, J. & Contractor, N. Trust amongst rogues? A hypergraph approach for comparing clandestine trust networks in MMOGs. 5th AAAI Conf. on Web. and Soc. Med. (2011).
Bakshy, E., Simmons, M. P., Huffaker, D. A., Teng, C. Y. & Adamic, L. A. The social dynamics of economic activity in a virtual world. 4th AAAI Conf. on Web. and Soc. Med. (2010).
Lieberman, M. B. & Montgomery, D. B. First-mover advantages. Strat. Mgmt. J. 9, 41–58 (1988).
Acknowledgements
We thank Cris Moore, Sid Redner, Tim Brown, Christopher Aicher, Dan Larremore, Abigail Jacobs, Winter Mason, FearfulSpoon, Stilted Fox, AngryKnife, jizackalyn and TOURIST1224 for helpful conversations, and Chris Schenk for help developing the data acquisition system. This work was supported in part by the James S. McDonnell Foundation.
Author information
Authors and Affiliations
Contributions
A.C. and S.M. designed and performed the research; A.C. and S.M. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supporting information (PDF 575 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Merritt, S., Clauset, A. Environmental structure and competitive scoring advantages in team competitions. Sci Rep 3, 3067 (2013). https://doi.org/10.1038/srep03067
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03067
This article is cited by
-
Ape parasite origins of human malaria virulence genes
Nature Communications (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.