Abstract
In directed networks, reciprocal links have dramatic effects on dynamical processes, network growth and higher-order structures such as motifs and communities. While the reciprocity of binary networks has been extensively studied, that of weighted networks is still poorly understood, implying an ever-increasing gap between the availability of weighted network data and our understanding of their dyadic properties. Here we introduce a general approach to the reciprocity of weighted networks and define quantities and null models that consistently capture empirical reciprocity patterns at different structural levels. We show that, counter-intuitively, previous reciprocity measures based on the similarity of mutual weights are uninformative. By contrast, our measures allow to consistently classify different weighted networks according to their reciprocity, track the evolution of a network's reciprocity over time, identify patterns at the level of dyads and vertices and distinguish the effects of flux (im)balances or other (a)symmetries from a true tendency towards (anti-)reciprocation.
Similar content being viewed by others
Introduction
The study of link reciprocity in binary directed networks1,2, or the tendency of vertex pairs to form mutual connections, has received an increasing attention in recent years3,4,5,6,7,8,9,10,11,12,13,14. Among other things, reciprocity has been shown to be crucial in order to classify3 and model4 directed networks, understand the effects of network structure on dynamical processes (e.g. diffusion or percolation processes5,6,7), explain patterns of growth in out-of-equilibrium networks (as in the case of the Wikipedia8 or the World Trade Web9,10) and study the onset of higher-order structures such as correlations11,12 and triadic motifs13,14,15,16. In networks that aggregate temporal information such as e-mail or phone-call networks, reciprocity also provides a measure of the simplest feed-back process occurring in the network, i.e. the tendency of a vertex to respond to another vertex stimulus. Finally, reciprocity quantifies the information loss determined by projecting a directed network into an undirected one: if the reciprocity of the original network is maximum, the full directed information can be retrieved from the undirected projection; on the other hand, no reciprocity implies a maximum uncertainty about the directionality of the original links that have been converted into undirected ones3. In particular intermediate cases, significant directed information can be retrieved from an undirected projection using the knowledge of reciprocity9. In general, reciprocity is the main quantity characterizing the possible dyadic patterns, i.e. the possible types of connections between two vertices.
While the reciprocity of binary networks has been studied extensively, that of weighted networks has received much less attention17,18,19,20, because of a more complicated phenomenology at the dyadic level. While in a binary graph it is straightforward to say that a link from vertex i to vertex j is reciprocated if the link from j to i is also there, in a weighted network there are clear complications. Given a link of weight wij > 0 from vertex i to vertex j, how can we assess, in terms of the mutual link of weight wji, whether the interaction is reciprocated? While wji = 0 (no link from j to i) clearly signals the absence of reciprocation, what about a value wji > 0 but such that  ? This complication has generally led to two approaches to the study of directionality in weighted networks: one assuming (either explicitly or implicitly) that perfect reciprocity corresponds to symmetric weights (wij = wji)17,19,20 and one looking for deviations from such symmetry by studying net flows (or imbalances), defined as wij − wji21. In the latter approach, significant information about the original weights, including their reciprocity, is lost: the original network produces the same results as any other network where
? This complication has generally led to two approaches to the study of directionality in weighted networks: one assuming (either explicitly or implicitly) that perfect reciprocity corresponds to symmetric weights (wij = wji)17,19,20 and one looking for deviations from such symmetry by studying net flows (or imbalances), defined as wij − wji21. In the latter approach, significant information about the original weights, including their reciprocity, is lost: the original network produces the same results as any other network where  and
and  . Since Δij is arbitrary, this approach cannot distinguish networks that have very different symmetry properties. In particular, maximally asymmetric (i.e. Δij = −wji, implying
. Since Δij is arbitrary, this approach cannot distinguish networks that have very different symmetry properties. In particular, maximally asymmetric (i.e. Δij = −wji, implying  whenever
whenever  ) and maximally symmetric networks (i.e.
) and maximally symmetric networks (i.e.  , implying
, implying  ), which are treated as opposite in the first approach, are indistinguishable in the second one. Consider, for example, two nodes a and b linked by the asymmetric weights wab = 0 and wba = 10: the imbalance wba − wab is the same as if they were an almost symmetric dyad with wab = 104 and
), which are treated as opposite in the first approach, are indistinguishable in the second one. Consider, for example, two nodes a and b linked by the asymmetric weights wab = 0 and wba = 10: the imbalance wba − wab is the same as if they were an almost symmetric dyad with wab = 104 and  .
.
In addition to the above limitations, it has become increasingly clear that the heterogeneity of vertices, which in weighted networks is primarily reflected into a generally very broad distribution of the strength (total weight of the links entering or exiting a vertex22), must be taken into account in order to build an adequate null model of a network23,24,25,26,27,28,29,30,31,32,33,34. Indeed, the different intrinsic tendencies of individual vertices to establish and/or strengthen connections have a strong impact on many other structural properties and the reciprocity is no exception. It is therefore important to account for such irreducible heterogeneity by treating local properties such as the strength (or the degree in the binary case) as constraints defining a null model for the network14. While null models of weighted networks are generally computationally demanding32,33, recently a fast and analytical method providing exact expressions characterizing both binary and weighted networks with constraints has been proposed14. This allows us, for the first time, to have mathematical expressions characterizing the behaviour of topological properties under the null model considered. In this paper we extend those results, in order to propose new mathematical definitions of reciprocity in the weighted case and to evaluate their behaviour exactly under various null models that introduce different constraints. This also allows us to assess whether an observed asymmetry between reciprocal links is consistent with fluctuations around a balanced but noisy average, or whether it a statistically robust signature of imbalance. Finally, we introduce models that successfully reproduce the observed patterns by introducing either a correct global reciprocity level or more stringent constraints on the local reciprocity structure.
Results
We first introduce measures of reciprocity which meet three criteria simultaneously: 1) if applied to a binary network, they must reduce to their well-known unweighted counterparts; 2) they must allow a consistent analysis across all structural levels, from dyad-specific through vertex-specific to network-wide; 3) they must have a mathematically controlled behaviour under null models with different constraints, thus disentangling reciprocity from other sources of (a)symmetry. Then, we discuss the differences with respect to other inadequate measures of ‘symmetry’, show our empirical results and introduce theoretical models aimed at reproducing the reciprocity structure of real weighted networks.
Dyad-specific measures
We consider a directed weighted network specified by the weight matrix W, where the entry wij indicates the weight of the directed link from vertex i to vertex j, including the case wij = 0 indicating the absence of such link. For simplicity, we assume no self-loops (i.e. wii = 0 ∀i), as the latter carry no information about reciprocity (in any case, allowing for self-loops is straightforward in our approach). As Fig. 1 shows, we can always decompose each pair (wij, wji) of reciprocal links into a bidirectional (fully reciprocated) interaction, plus a unidirectional (non reciprocated) interaction.
Formally, we can define the reciprocated weight between i and j (the symmetric part) as

and the non-reciprocated weight from i to j (the asymmetric part) as

Note that if  then
then  , which makes the unidirectionality manifest. We can also define
, which makes the unidirectionality manifest. We can also define

as the non-reciprocated weight from j to i and restate the unidirectionality property in terms of the fact that  and
and  cannot be both nonzero. Thus any dyad (wij, wji) can be equivalently decomposed as (
cannot be both nonzero. Thus any dyad (wij, wji) can be equivalently decomposed as ( ,
,  ,
,  ). If the network is binary, all the above variables are either 0 or 1 and our decomposition coincides with a well studied dyadic decomposition3,4,5,6.
). If the network is binary, all the above variables are either 0 or 1 and our decomposition coincides with a well studied dyadic decomposition3,4,5,6.
Vertex-specific measures
From the above fundamental dyadic quantities it is possible to define reciprocity measures at the more aggregate level of vertices. We recall that the out- and in-strength of a vertex i are defined as the sum of the weights of the out-going and in-coming links respectively:

In analogy with the so-called degree sequence in binary networks, we denote the vector of values { } as the out-strength sequence and the vector of values {
} as the out-strength sequence and the vector of values { } as the in-strength sequence. Using eqs.(1–3), we can split the above quantities into their reciprocated and non-reciprocated contributions, as has been proposed for vertex degrees in binary networks3,4. We first define the reciprocated strength
} as the in-strength sequence. Using eqs.(1–3), we can split the above quantities into their reciprocated and non-reciprocated contributions, as has been proposed for vertex degrees in binary networks3,4. We first define the reciprocated strength

which measures the overlap between the in-strength and the out-strength of vertex i, i.e. the portion of strength of that vertex which is fully reciprocated by its neighbours. Then we define the non-reciprocated out-strength as

and the non-reciprocated in-strength as

The last two quantities represent the non-reciprocated components of  and
and  respectively, i.e. the out-going and in-coming fluxes which exceed the inverse fluxes contributed by the neighbours of vertex i.
respectively, i.e. the out-going and in-coming fluxes which exceed the inverse fluxes contributed by the neighbours of vertex i.
Network-wide measures
Finally, we introduce weighted measures of reciprocity at the global, network-wide level. Recall that the total weight of the network is

Similarly, we denote the total reciprocated weight as

Extending a common definition widely used for binary graphs1,2,3, we can then define the weighted reciprocity of a weighted network as

If all fluxes are perfectly reciprocated (i.e. W↔ = W) then r = 1, whereas in absence of reciprocation (i.e. W↔ = 0) then r = 0. In the SI we discuss the difference between our definitions and other attempts to characterize the reciprocity of weighted networks17,18,19,20.
Just like its binary counterpart, eq.(10) is informative only after a comparison with a null model (NM) is made, i.e. with a value 〈r〉NM expected for a network having some property in common (e.g. the number of vertices N and/or the total weight W) with the observed one. As a consequence, networks with different empirical values of such quantities cannot be consistently ranked in terms of the measured value of r. An analogous problem is encountered in the binary case3 and has been solved by introducing a transformed quantity that we generalize to the present setting as

The sign of ρNM is directly informative of an increased, with respect to the null model, tendency to reciprocate (ρNM > 0) or to avoid reciprocation (ρNM < 0). If ρNM is consistent with zero (within a statistical error that we quantify in the SI), then the observed level of reciprocity is compatible with what merely expected by chance under the null model. The literature on null models of networks is very vast4,14,23,24,25,26,29,30,34,35,36,37,38,39. In this paper we adopt a recent analytical method14 and extend it in order to study the reciprocity of weighted networks. The three null models we consider are described in the Methods and SI.
Reciprocity versus symmetry
We stress that the alternative approaches17,18,19,20 are all based on the assumption that the maximum level of reciprocity corresponds to a symmetric network where wij = wji, so that deviations from this symmetric situation are interpreted as signatures of incomplete reciprocity. This is actually incorrect: independently of other properties of the observed network, the symmetry of weights (i.e. wij = wji) is completely uninformative about the reciprocity structure, for two reasons.
First, in networks with broadly distributed strengths (as in most real-world cases) the attainable level of symmetry strongly depends on the in- and out-strengths of the end-point vertices: unless  for all vertices, it becomes more and more difficult, as the heterogeneity of strengths across vertices increases, to match all the constraints required to ensure that wij = wji for all pairs. Therefore, even networks that maximize the level of reciprocity, given the values of the strengths of all vertices, are in general not symmetric.
for all vertices, it becomes more and more difficult, as the heterogeneity of strengths across vertices increases, to match all the constraints required to ensure that wij = wji for all pairs. Therefore, even networks that maximize the level of reciprocity, given the values of the strengths of all vertices, are in general not symmetric.
On the other hand, in networks with balance of flows at the vertex level ( for all vertices) an average symmetry of weights (〈wij〉 = 〈wji〉) is automatically achieved by pure chance, even without introducing a tendency to reciprocate (see SI). In many real networks (including examples we study below), the balance of flows at the vertex level is actually realized, either exactly or approximately, as the result of conservation laws (e.g. mass or current balance). In those cases, the symmetry of weights should not be interpreted as a preference for reciprocated interactions.
for all vertices) an average symmetry of weights (〈wij〉 = 〈wji〉) is automatically achieved by pure chance, even without introducing a tendency to reciprocate (see SI). In many real networks (including examples we study below), the balance of flows at the vertex level is actually realized, either exactly or approximately, as the result of conservation laws (e.g. mass or current balance). In those cases, the symmetry of weights should not be interpreted as a preference for reciprocated interactions.
In the SI we also show that measures based on the correlation between wij and wji are flawed. Similarly, studies of asymmetry focusing on the differences wij − wji are severely limited by the fact that the observed imbalances might actually be fluctuations around a zero average (〈wij − wji〉 = 0), irrespective of the level of reciprocity. Thus, reciprocity and symmetry are two completely different structural aspects10.
Reciprocity rankings classify weighted networks
We now carry out an empirical analysis of several real weighted networks using our definitions introduced above. We start with the global quantities r and ρNM defined in eqs.(10) and (11). In Table I we report the analysis of 70 biological, social and economic networks40,41,42,43,44,45,46,47,48,49,50.
All networks display a nontrivial weighted reciprocity structure (i.e. ρ ≠ 0), which differs from that predicted by the 3 null models considered (WCM, BCM and WRG: see Methods and SI). This means that the imposed constraints cannot account for the observed reciprocity. Remarkably, we also find that networks of the same type systematically display similar values of ρ: for a given choice of the null model, the resulting reciprocity ranking provides a consistent (non-overlapping) classification of networks. However, different null models provide different estimates of reciprocity and rank the same networks differently. Some networks (social networks41,42,43,44,45,46 and the World Trade Web47) always show a positive reciprocity, while others (foodwebs50) always show a negative reciprocity, irrespective of the null model. However, other networks (interbank networks48) are classified as weakly but positively reciprocal under the WCM, but as strongly negatively reciprocal under the BCM and the WRG. In one case (neural network49), the estimated level of reciprocity can be slightly positive, negative, or even consistent with zero depending on the null model. As a consequence, the 5 interbank networks are more reciprocal than the neural network under the WCM, while the ranking is inverted under the BCM and the WRG. Since the WCM is the most conservative model, preserving most information from empirical data, we choose to rank the networks in the Table using ρWCM.
Importantly, we find that all weighted rankings are quite different from the binary analysis-based ranking3. While the various snapshots of the World Trade Web are systematically found to be strongly and sometimes almost perfectly reciprocal in the binary case (0.68 ≤ ρRG ≤ 0.95 under the binary Random Graph model3), here we find them to be less reciprocal than social networks if the additional weighted information is taken into account. Also, while the neural network of C. elegans has a strong binary reciprocity (ρRG = 0.413), here we find it to have a very weak (under the WCM), consistent with zero (under the WRG), or even negative (under the BCM) weighted reciprocity. These important differences show that the reciprocity of weighted networks is nontrivial and irreducible to a binary description.
The role of node imbalances
The two differences between the WCM and the WRG (see Methods and SI) are node imbalance (〈 〉 and 〈
〉 and 〈 〉 are equal in the WRG and different in the WCM) and node heterogeneity (the expected strenghts of all vertices are equal in the WRG and broadly distributed in the WCM). We can use the BCM as an intermediate model in order to disentangle the role of these two differences in producing the observed deviations between ρWCM and ρWRG. The BCM preserves node heterogeneity but assumes node balance by regarding the observed difference between the in- and out-strength of each vertex as a statistical fluctuation around a balanced average (see SI). As we show in Fig. 2, some real networks (such as foodwebs and the World Trade Web) indeed appear to display very small fluctuations around this type of node balance. In foodwebs, where edges represent stationary flows of energy among species, the almost perfect balance is due to an approximate biomass or energy conservation at each vertex. In the World Trade Web, where edges represent the amount of trade among world countries, the approximate balance of vertex flows is due to the fact that countries tend to minimize the difference between their total import and their total exports, i.e. they try to ‘balance their payments’51.
〉 are equal in the WRG and different in the WCM) and node heterogeneity (the expected strenghts of all vertices are equal in the WRG and broadly distributed in the WCM). We can use the BCM as an intermediate model in order to disentangle the role of these two differences in producing the observed deviations between ρWCM and ρWRG. The BCM preserves node heterogeneity but assumes node balance by regarding the observed difference between the in- and out-strength of each vertex as a statistical fluctuation around a balanced average (see SI). As we show in Fig. 2, some real networks (such as foodwebs and the World Trade Web) indeed appear to display very small fluctuations around this type of node balance. In foodwebs, where edges represent stationary flows of energy among species, the almost perfect balance is due to an approximate biomass or energy conservation at each vertex. In the World Trade Web, where edges represent the amount of trade among world countries, the approximate balance of vertex flows is due to the fact that countries tend to minimize the difference between their total import and their total exports, i.e. they try to ‘balance their payments’51.
In-strength  versus out-strength
versus out-strength  in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (note that the increase in reciprocity is not necessarily associated with an increase in symmetry).
in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (note that the increase in reciprocity is not necessarily associated with an increase in symmetry).
As we show in the SI, the balance of vertex flows implies that, even without introducing a tendency to reciprocate, the expected mutual weights are equal: 〈wij〉 = 〈wji〉. This implies a larger expected reciprocated weight 〈W↔〉 in the BCM than in the WCM, so that ρWCM > ρBCM, as confirmed by Table I. However, we find that ρBCM and ρWRG are always very similar, while they can be very different from ρWCM. This means that node imbalances, even when very weak, can have a major effect on the expected level of reciprocity. Surprisingly, we find that this effect is much stronger than that of the strikingly more pronounced node heterogeneity. Correctly filtering out the effects of flux balances or other symmetries can lead to counter-intuitive results: the most reciprocal of the four networks (the social network, see Table I) is one of the least symmetric ones (see Fig. 2d), whereas the least reciprocal of the four networks (the foodweb, see Table I) is the most symmetric one (see Fig. 2a).
Time evolution and fluctuations
Since ρ consistently ranks the reciprocity of networks with different properties, it can also track the evolution of reciprocity in a network that changes over time. For this reason, in our dataset we have included 53 yearly snapshots of the World Trade Web, from year 1948 to 20009,47. In Fig. 3 we show the evolution of r, 〈r〉 and ρ under the three null models. The plots confirm that, unlike ρ, r is not an adequate indicator of the evolution of reciprocity, since the baseline expected value 〈r〉 (under every null model) also changes in time as a sort of moving target (Fig. 3a).
Temporal evolution of the reciprocity of the World Trade Web during the 53 years from 1948 to 2000: (a) observed value of r (blue) and its expected values 〈r〉NM under the Weighted Configuration Model (red), the Balanced Configuration Model (green) and the Weighted Random Graph (orange); (b) evolution of ρNM under the same 3 null models as above.
Note that 〈r〉WCM fluctuates much more than 〈r〉WRG and 〈r〉BCM and its fluctuations resemble those of the observed value r (see Fig. 3a). This is due to the fact that, while all snapshots of the network are characterized by ‘static’ fluctuations of the empirical strengths of vertices around the balanced flux condition  (like those in shown in Fig. 2c for the year 2000), these fluctuations have different entities in different years. Changes in the size of ‘static’ fluctuations produce the ‘temporal’ fluctuations observed in the evolution of 〈r〉WCM and partly also in the observed value r, confirming the important role of node (im)balances. After controlling for the time-varying entity of node imbalances (using the WCM), we indeed find that the fluctuations of ρWCM are less pronounced than those of ρBCM and ρWRG (see Fig. 3b). However, the fluctuations of r and 〈r〉WCM do not cancel out completely and their resulting net effect (the trend of ρWCM) is still significant, indicating the strongest level of reciprocity across the three null models.
(like those in shown in Fig. 2c for the year 2000), these fluctuations have different entities in different years. Changes in the size of ‘static’ fluctuations produce the ‘temporal’ fluctuations observed in the evolution of 〈r〉WCM and partly also in the observed value r, confirming the important role of node (im)balances. After controlling for the time-varying entity of node imbalances (using the WCM), we indeed find that the fluctuations of ρWCM are less pronounced than those of ρBCM and ρWRG (see Fig. 3b). However, the fluctuations of r and 〈r〉WCM do not cancel out completely and their resulting net effect (the trend of ρWCM) is still significant, indicating the strongest level of reciprocity across the three null models.
While a binary analysis of the WTW9,10 detected an almost monotonic increase of the reciprocity, with a marked acceleration in the 90's, we find that the weighted reciprocity has instead undergone a rapid decrease over the same decade: this counter-intuitive result confirms that the information conveyed by a weighted analysis of reciprocity is nontrivial and irreducible to the binary picture.
Local reciprocity structure
We now focus on the reciprocity structure at the local level of vertices, i.e. on the reciprocated and non-reciprocated strength  ,
,  and
and  defined in eqs.(5–7). As clear from eq.(9), this allows us to analyse how different vertices contribute to the overall value of W↔ and hence to r. In order to assess whether the vertex-specific reciprocity structure is significant, rather than merely a consequence of the local topological properties of vertices, we compare the observed value of
defined in eqs.(5–7). As clear from eq.(9), this allows us to analyse how different vertices contribute to the overall value of W↔ and hence to r. In order to assess whether the vertex-specific reciprocity structure is significant, rather than merely a consequence of the local topological properties of vertices, we compare the observed value of  ,
,  and
and  with their expected values under the WCM and the BCM. Unlike the WRG, these models preserve the total strength
with their expected values under the WCM and the BCM. Unlike the WRG, these models preserve the total strength  of each vertex, thus filtering out the effects of the observed heterogenity of vertices. In Fig. 4 we show the observed and expected values of the (non-)reciprocated strength versus the total strength
of each vertex, thus filtering out the effects of the observed heterogenity of vertices. In Fig. 4 we show the observed and expected values of the (non-)reciprocated strength versus the total strength  for the four networks already shown in Fig. 2 in order of increasing reciprocity.
for the four networks already shown in Fig. 2 in order of increasing reciprocity.
Relationship between total ( ) and reciprocated (
) and reciprocated ( ) or non-reciprocated (
) or non-reciprocated ( ) strength in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (black: real data, green: Weighted Configuration Model, red: Balanced Configuration Model).
) strength in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (black: real data, green: Weighted Configuration Model, red: Balanced Configuration Model).
For the anti-reciprocal networks with ρ < 0 (the foodweb and, under some null model, the neural network), the dominant and less fluctuating contribution to  comes from the non-reciprocated strength and therefore we choose to plot
comes from the non-reciprocated strength and therefore we choose to plot  versus
versus  (Fig. 4a–b). Conversely, for the positively reciprocal networks with ρ > 0 (the World Trade Web and the social network) the dominant contribution comes from the reciprocated strength, so we consider
(Fig. 4a–b). Conversely, for the positively reciprocal networks with ρ > 0 (the World Trade Web and the social network) the dominant contribution comes from the reciprocated strength, so we consider  versus
versus  (Fig. 4c–d).
(Fig. 4c–d).
We found very rich and diverse patterns. In all networks, the selected quantity displays an approximately monotonic increase with  . Qualitatively, this increasing trend is also reproduced by the two null models. However, we systematically find large differences between the latter and real data. In the foodweb (Fig. 4a), the observed values of the non-reciprocated strength
. Qualitatively, this increasing trend is also reproduced by the two null models. However, we systematically find large differences between the latter and real data. In the foodweb (Fig. 4a), the observed values of the non-reciprocated strength  are always larger than the expected values (note that the separation between the two trends is exponentially larger than it appears in a log-log plot). This shows that each vertex contributes, roughly proportionally to its total strength, to the overall anti-reciprocity of this network (W↔ < 〈W↔〉NM and hence ρNM < 0, see Table I). By contrast, in the neural network (Fig. 4b) some vertices (mostly, but not uniquely those with large
are always larger than the expected values (note that the separation between the two trends is exponentially larger than it appears in a log-log plot). This shows that each vertex contributes, roughly proportionally to its total strength, to the overall anti-reciprocity of this network (W↔ < 〈W↔〉NM and hence ρNM < 0, see Table I). By contrast, in the neural network (Fig. 4b) some vertices (mostly, but not uniquely those with large  ) have a larger non-reciprocated strength than expected under the null models, while for other vertices (mostly those with small
) have a larger non-reciprocated strength than expected under the null models, while for other vertices (mostly those with small  ) the opposite is true. This shows that the weak (and nearly consistent with zero, see Table I) overall reciprocity of this network is the result of several opposite contributions of different vertices, that cancel each other almost completely. The World Trade Web (Fig. 4c) also shows a combination of deviations in both directions, even if in this case for the vast majority of vertices the observed reciprocated strength is larger than the expected one. This results in the overall positive reciprocity of the network, but again in a such a way that the global information is not reflected equally into the local one. Finally, the social network (Fig. 4d) displays a behaviour analogous, but opposite, to that of the foodweb: the observed reciprocated strength of each vertex systematically exceeds its expected value and gives a proportional contribution to the overall positive reciprocity.
) the opposite is true. This shows that the weak (and nearly consistent with zero, see Table I) overall reciprocity of this network is the result of several opposite contributions of different vertices, that cancel each other almost completely. The World Trade Web (Fig. 4c) also shows a combination of deviations in both directions, even if in this case for the vast majority of vertices the observed reciprocated strength is larger than the expected one. This results in the overall positive reciprocity of the network, but again in a such a way that the global information is not reflected equally into the local one. Finally, the social network (Fig. 4d) displays a behaviour analogous, but opposite, to that of the foodweb: the observed reciprocated strength of each vertex systematically exceeds its expected value and gives a proportional contribution to the overall positive reciprocity.
Note that, while the striking similarity between the predictions of the WCM and the BCM in the foodweb and in the World Trade Web is not surprising, because of the very close node-balance relationship  in these two networks (see Fig. 2a and 2c), in the neural network and in the social network the similarity between the predictions of the two null models is nontrivial, since node balance is strongly violated in these cases (see Fig. 2b and 2d).
in these two networks (see Fig. 2a and 2c), in the neural network and in the social network the similarity between the predictions of the two null models is nontrivial, since node balance is strongly violated in these cases (see Fig. 2b and 2d).
Having shown that the reciprocity of real weighted networks is very pronounced, we conclude our study by introducing a class of models aimed at correctly reproducing the observed patterns. To this end, rather than proposing untestable models of network formation, we expand the null models we have considered above by enforcing additional or alternative constraints on the reciprocity structure. This approach leads us to define the weighted counterparts of the binary Exponential Random Graphs (or p* models) with reciprocity1,2 and their generalizations3,4,10. We first define three models that exactly reproduce, besides the observed heterogeneity of the strength of vertices, the observed global level of reciprocity (i.e. such that W↔ = 〈W↔〉 and W = 〈W〉, implying ρ = 0). Our aim is to check whether this is enough in order to reproduce the more detailed, local reciprocity structure.
In the first model (‘Weighted Reciprocity Model’, see SI), the constraints are  and
and  for each vertex (as in the WCM) and additionally W↔. This model is the analogue of the binary reciprocity model by Holland and Leinhardt1 and replicates the overall reciprocity r exactly. However, as we discuss in the SI, it is best suited to reproduce networks that are anti-reciprocal or, more precisely, less reciprocal than the WCM (ρWCM < 0). Therefore, in our analysis we can only apply it to the foodwebs. In Fig. 5a we show our results on the Everglades web. For the sake of comparison with Fig. 4a, we plot
for each vertex (as in the WCM) and additionally W↔. This model is the analogue of the binary reciprocity model by Holland and Leinhardt1 and replicates the overall reciprocity r exactly. However, as we discuss in the SI, it is best suited to reproduce networks that are anti-reciprocal or, more precisely, less reciprocal than the WCM (ρWCM < 0). Therefore, in our analysis we can only apply it to the foodwebs. In Fig. 5a we show our results on the Everglades web. For the sake of comparison with Fig. 4a, we plot  as a function of
as a function of  . We find that, quite surprisingly, the model does not significantly improve the accordance between real and expected trends produced by the WCM and BCM (see Fig. 4a). The only difference with respect to the latter is that now a few vertices with very large
. We find that, quite surprisingly, the model does not significantly improve the accordance between real and expected trends produced by the WCM and BCM (see Fig. 4a). The only difference with respect to the latter is that now a few vertices with very large  lie below the expected trend, while all the other vertices continue to lie above it (Fig. 5a) producing an overall ρ = 0: so, even if all vertices appeared to contribute evenly and proportionally to the global anti-reciprocity (see Fig. 4a), adding the latter as an overall constraint is not enough in order to capture the local reciprocity structure.
lie below the expected trend, while all the other vertices continue to lie above it (Fig. 5a) producing an overall ρ = 0: so, even if all vertices appeared to contribute evenly and proportionally to the global anti-reciprocity (see Fig. 4a), adding the latter as an overall constraint is not enough in order to capture the local reciprocity structure.
Relationship between total ( ) and reciprocated (
) and reciprocated ( ) or non-reciprocated (
) or non-reciprocated ( ) strength in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (black: real data, blue: the Weighted Reciprocity Model, orange: the Non-reciprocated Strength Model, green: the Reciprocated Strength Model; all such models reproduce the global level of reciprocity but not necessarily the local reciprocity structure).
) strength in four weighted networks in increasing order of reciprocity ρ: (a) the Everglades Marshes foodweb, (b) the neural network of C. elegans, (c) the World Trade Web in the year 2000 and (d) the social network of a fraternity at West Virginia College (black: real data, blue: the Weighted Reciprocity Model, orange: the Non-reciprocated Strength Model, green: the Reciprocated Strength Model; all such models reproduce the global level of reciprocity but not necessarily the local reciprocity structure).
In our second model (‘Non-reciprocated Strength Model’, see SI), the constraints are  ,
,  (for each vertex) and W↔. This slightly relaxed model (potentially) generates all levels of reciprocity r. However, it does not automatically reproduce the in- and out-strength sequences, therefore it is only appropriate for networks where
(for each vertex) and W↔. This slightly relaxed model (potentially) generates all levels of reciprocity r. However, it does not automatically reproduce the in- and out-strength sequences, therefore it is only appropriate for networks where  and
and  are the dominant contributions to
are the dominant contributions to  and
and  respectively, so that specifying the former largely specifies the latter as well. So, even if now there are no mathematical restrictions, this model is again only appropriate for networks with negative reciprocity (ρWCM < 0). In Fig. 5a we show the predictions of this model on the foodweb: note that, as compared to the previous model, now the quantity
respectively, so that specifying the former largely specifies the latter as well. So, even if now there are no mathematical restrictions, this model is again only appropriate for networks with negative reciprocity (ρWCM < 0). In Fig. 5a we show the predictions of this model on the foodweb: note that, as compared to the previous model, now the quantity  is exactly reproduced by construction, while
is exactly reproduced by construction, while  is not reproduced, with most vertices lying above the expected trend and a few dominating ones lying below it. So the result is even worse than before. In Fig. 5b we also show the performance of this model on the neural network (which actually displays ρWCM ≈ 0, even if it still has negative reciprocity under other null models, see Table I): even if the agreement is now much better, most data continue to lie either above or below the expected curve, confirming that the reciprocated strengths cannot be simply reconciled with the total strengths. Note however that for networks with smaller ρ this model becomes more accurate and in the limit W↔ → 0 it exactly reproduces all the strength sequences of any network.
is not reproduced, with most vertices lying above the expected trend and a few dominating ones lying below it. So the result is even worse than before. In Fig. 5b we also show the performance of this model on the neural network (which actually displays ρWCM ≈ 0, even if it still has negative reciprocity under other null models, see Table I): even if the agreement is now much better, most data continue to lie either above or below the expected curve, confirming that the reciprocated strengths cannot be simply reconciled with the total strengths. Note however that for networks with smaller ρ this model becomes more accurate and in the limit W↔ → 0 it exactly reproduces all the strength sequences of any network.
Our third model (‘Reciprocated Strength Model’, see SI) is a ‘dual’ one appropriate in the opposite regime of strong positive reciprocity (i.e. ρWCM > 0, especially in the limit ρWCM → 1). The constraints are now  (for each vertex) and the total weight W (note that, as a consequence, also the non-reciprocated total weight W→ ≡ W − W↔ is kept fixed). This model is most appropriate for networks where
(for each vertex) and the total weight W (note that, as a consequence, also the non-reciprocated total weight W→ ≡ W − W↔ is kept fixed). This model is most appropriate for networks where  is the dominant contribution to
is the dominant contribution to  . In Fig. 5c we show the predictions of this model on the World Trade Web. Now
. In Fig. 5c we show the predictions of this model on the World Trade Web. Now  is obviously always reproduced, while
is obviously always reproduced, while  instead is not reproduced for all vertices. In Fig. 5d we show the results for the social network and in this case we find that the model reproduces real data remarkably well. This confirms that the model is particularly appropriate for strongly reciprocal networks. We therefore find that, as in the dual case discussed above, if the overall reciprocity is moderate then the constraints are in general not enough in order to characterize the local reciprocity structure. However, in networks with strong overall reciprocity, this model accurately (and exactly in the limit W→ → 0) reproduces all the local reciprocity structure.
instead is not reproduced for all vertices. In Fig. 5d we show the results for the social network and in this case we find that the model reproduces real data remarkably well. This confirms that the model is particularly appropriate for strongly reciprocal networks. We therefore find that, as in the dual case discussed above, if the overall reciprocity is moderate then the constraints are in general not enough in order to characterize the local reciprocity structure. However, in networks with strong overall reciprocity, this model accurately (and exactly in the limit W→ → 0) reproduces all the local reciprocity structure.
Discussion
The above three models produce the correct level of global reciprocity (i.e. 〈r〉 = r or ρ = 0) but not necessarily the correct local reciprocity structure. In networks with strong (either positive or negative) reciprocity, the local reciprocity structure can be simply inferred from the global one, plus some information about the heterogeneity of vertices (some strength sequence). Conversely, in networks with moderate reciprocity the local patterns are irreducible to any overall information and thus constitute intrinsic heterogeneous features. In this case, it is unavoidable to use a model that fully reproduces the three quantities  ,
,  and
and  separately for each vertex, by treating them as constraints. In the SI we describe this model, that we denote as the Weighted Reciprocated Configuration Model (WRCM) in detail. Using this model, all the plots in Fig. 5 are automatically reproduced exactly, by construction. Therefore we believe that this model represents an important starting point for future analyses of higher-order topological properties in weighted networks. In particular, we foresee two main applications.
separately for each vertex, by treating them as constraints. In the SI we describe this model, that we denote as the Weighted Reciprocated Configuration Model (WRCM) in detail. Using this model, all the plots in Fig. 5 are automatically reproduced exactly, by construction. Therefore we believe that this model represents an important starting point for future analyses of higher-order topological properties in weighted networks. In particular, we foresee two main applications.
The first application is to the analysis of weighted ‘motifs’, i.e. the abundances of all topologically distinct subgraphs of three or four vertices13,15. In the binary case, it has been realized that such subgraphs are important building blocks of large networks and that their abundance is not trivially explained in terms of the dyadic structure. This result can only be obtained by comparing the observed abundances with their expectation values under a null model that separately preserves the number of reciprocated and non-reciprocated (in-coming and out-going) links of each vertex. In the weighted case, no similar analysis has been carried out so far, because of the lack of an analogous method, like the WRCM defined here, to control for the reciprocated and non-reciprocated connectivity properties separately.
The second application is to the problem of community detection52 in weighted directed networks, i.e. the identification of densely connected modules of vertices. Most approaches attempt to find the partition of the network that maximizes the so-called ‘modularity’, i.e. the total difference between the observed weights of intra-community links and their expected values under the WCM. In networks where the observed reciprocity is not reproduced by the WCM (as all networks in the present study), the difference between observed and expected weights is not necessarily due to the presence of community structure, as it also receives a (potentially strong) contribution by the reciprocity. This means that, in order to filter out the effects of reciprocity from community structure, in the modularity function one should replace the expected values under the WCM with the expected values under the WRCM.
The ever-increasing gap between the growth of data about weighted networks and our poor understanding of their dyadic properties led us to propose a rigorous approach to the reciprocity of weighted networks. We showed that real networks systematically display a rich and diverse reciprocity structure, with several interesting patterns at the global and local level. We believe that our results form an important starting point to answer many open questions about the effect of reciprocity on higher-order structural properties and on dynamical processes taking place on real weighted networks.
Methods
Equation (11) in the Results section introduces the quantity ρNM, as the normalized difference between the observed value of the weighted reciprocity r and its expected value under a chosen null model 〈r〉NM. The introduction of ρNM has two important consequences. Firstly, networks with different parameters can be ranked from the most to the least reciprocal using the measured value of ρNM. Secondly and consequently, the reciprocity of a network that evolves in time can be tracked dynamically using ρNM even if other topological properties of the network change (as is typically the case). Clearly, the above considerations apply not only to the global quantity r, but also to the edge-and vertex-specific definitions we have introduced in eqs.(1–3) and (5–7). For this reason, in the SI we introduce and study three important null models in great detail. We briefly describe these models below.
Null models: the Weighted Random Graph model
To start with, we consider a network model with the same total weight W as the real network but with no tendency towards or against reciprocation, i.e. a directed version of the Weighted Random Graph (WRG) model36. This allows us to quantify for the first time the baseline level of reciprocity 〈r〉WRG expected by chance in a directed network with given total weight. However, this null model is severely limited by the fact that it is completely homogeneous in two respects (see the SI): it generates networks where each vertex i has the same expected in- and out-strength ( ) and moreover this value is common to all vertices (〈si〉WRG = 〈s〉WRG µi).
) and moreover this value is common to all vertices (〈si〉WRG = 〈s〉WRG µi).
Null models: the Weighted Configuration model
A popular and more appropriate null model that preserves the observed intrinsic heterogeneity of vertices is one where all vertices have the same in-strength and out-strength as in the real network, i.e. the directed Weighted Configuration Model (WCM)30. In such model, since  and
and  , the two sources of homogeneity characterizing the WRG are both absent: each vertex has different values of the in-strength and out-strength and these values are also heterogeneously distributed across vertices. In other words, this model preserves the in- and out-strength sequences separately.
, the two sources of homogeneity characterizing the WRG are both absent: each vertex has different values of the in-strength and out-strength and these values are also heterogeneously distributed across vertices. In other words, this model preserves the in- and out-strength sequences separately.
Null models: the Balanced Configuration model
Another important null model that we introduce here for the first time is one that allows us to conclude whether the observed asymmetry of fluxes is consistent with a fluctuation around a balanced network (i.e. one where the net flow at each vertex is zero). This model, that we denote as the Balanced Configuration Model (BCM), is somewhat intermediate between the above two models, as it assumes (like the WRG) that the expected in- and out-strength of each vertex are the same, i.e. that the two observed values  and
and  are fluctuations around a common expected value
are fluctuations around a common expected value  , but at the same time preserves (as the WCM) the strong heterogeneity of vertices (i.e. in general 〈si〉BCM ≠ 〈sj〉BCM if i ≠ j). This model preserves the total strength
, but at the same time preserves (as the WCM) the strong heterogeneity of vertices (i.e. in general 〈si〉BCM ≠ 〈sj〉BCM if i ≠ j). This model preserves the total strength  of each vertex, but not the in- and out-strength separately.
of each vertex, but not the in- and out-strength separately.
Note that all the above null models preserve the total weight of the original network, i.e. 〈W〉NM = W. However, they do not automatically preserve the reciprocity (neither locally nor globally). Our aim is to understand whether the observed reciprocity can be simply reproduced by one of the null models (and is therefore trivial), or whether it deviates systematically from the null expectations. In the next section we show that the latter is true and that the reciprocity structure is a robust and novel pattern characterizing weighted networks.
A unifying formalism
As we show in the SI, it is possible to characterize all the above null models analytically and thus to calculate the required expected values exactly. Even if the final expressions are rather simple, their derivation is in some cases quite involved and requires further developments of mathematical results that have appeared relatively recently in the literature29,34,36. Moreover, the crucial step that fixes the values of the parameters of all models requires the application of a maximum-likelihood method that has been proposed by two of us only recently14. It is for the above reasons, we believe, that the reciprocity of weighted networks has not been studied as intensively as its binary counterpart so far. By putting all the pieces together, we are finally able to approach the problem in a consistent and rigorous way. Importantly, the framework wherein our null models are introduced (maximum-entropy ensembles of weighted networks with given properties) extends to the weighted case and at the same time formally unifies, recent randomization approaches proposed by physicists and well-established models of social networks introduced by statisticians, i.e. the so-called Exponential Random Graphs or p* models (see the SI). While a variety of specifications for the latter exist in the binary graph case2,37,38, very few results for weighted graphs are available39,53,54. Our contribution opens the way for the introduction of more general families of Exponential Random Graphs for weighted networks. Indeed, besides the null models discussed above, we will also introduce the first models that correctly reproduce the observed reciprocity structure, either at the global (but not necessarily local) level, or at the local (and consequently also global) level. It is worth mentioning that our approach makes use of exact analytical expressions and allows to find the correct values of the parameters both in the null models and in the models with reciprocity. By contrast, the common methods available in social network analysis to estimate binary Exponential Random Graphs rely on approximate techniques such as Markov Chain Monte Carlo or pseudo-likelihood approaches2,37,38. Another advantage is that the method we employ allows us to obtain the expected value of any topological property mathematically and in a time as short as that required in order to measure the same property on the original network14. Unlike other randomization approaches23,24, we do not need to computationally generate several randomized variants of the original network and take (approximate and generally biased35) sample averages over them.
Comparing real data with the above null models and the null models among themselves, allows us to separate different sources of heterogeneity observed in networks. This is a key step towards understanding the origin of the reciprocity structure of real weighted networks.
References
Holland, P. & Leinhardt, S. in Sociological Methodology. ed Heise, D. (Jossey-Bass, San Francisco), 1–45 (1975).
Wasserman, S. & Faust, K. Social Network Analysis. Cambridge University Press (Cambridge, New York) (1994).
Garlaschelli, D. & Loffredo, M. I. Patterns of Link Reciprocity in Directed Networks. Phys. Rev. Lett. 93, 268701 (2004).
Garlaschelli, D. & Loffredo, M. I. Multispecies grand-canonical models for networks with reciprocity. Phys. Rev. E 73, 015101 (2006).
Meyers, L. A., Newman, M. E. J. & Pourbohloul, B. Predicting epidemics on directed contact networks. J. Theor. Biol. 240, 400–418 (2006).
Boguna, M. & Serrano, M. A. Generalized percolation in random directed networks. Phys. Rev. E 72, 016106 (2005).
Perra, N. et al. PageRank equation and localization in the WWW. Europhys. Lett. 88, 48002 (2009).
Zlatic, V. & Stefancic, H. Model of Wikipedia growth based on information exchange via reciprocal arcs. EPL 93, 58005 (2011).
Garlaschelli, D. & Loffredo, M. I. Structure and evolution of the world trade network. Physica A 355(1), 138–144 (2005).
Garlaschelli, D., Ruzzenenti, F. & Basosi, R. Complex Networks and Symmetry I: a Review. Symmetry 2(3), 1683–1709 (2010).
Zamora-Lopez, G., Zlatic, V., Zhou, C., Stefancic, H. & Kurths, J. Reciprocity of networks with degree correlations and arbitrary degree sequences. Phys. Rev. E 77, 016106 (2008).
Zlatic, V. & Stefancic, H. Influence of reciprocal edges on degree distribution and degree correlations. Phys. Rev. E 80, 016117 (2009).
Stouffer, D. B., Camacho, J., Jiang, W. & Amaral, L. A. N. Evidence for the existence of a robust pattern of prey selection in food webs. Proc. R. Soc. B 274, 1931–1940 (2007).
Squartini, T. & Garlaschelli, D. Analytical maximum-likelihood method to detect patterns in real networks. New J. Phys. 13, 083001 (2011).
Milo, R. et al. Network Motifs: Simple Building Blocks of Complex Networks. Science 298, 824–827 (2002).
Squartini, T. & Garlaschelli, D. Triadic Motifs and Dyadic Self-Organization in the World Trade Network. Lec. Notes Comp. Sci. 7166, 24–35 (2012).
Kovanen, L., Saramaki, J. & Kaski, K. Reciprocity of mobile phone calls. Dynamics of Socio-Economic Systems 2(2), 138–151 (2011).
Fagiolo, G. Directed or Undirected? A New Index to Check for Directionality of Relations in Socio-Economic Networks. Econ. Bull. 3(34), 1–12 (2006).
Wang, C., Lizardo, O., Hachen, D., Strathman, A., Toroczkai, Z. & Chawla, N. A dyadic reciprocity index for repeated interaction networks. Network Science 1(1), 31–48 (2013).
Akoglu, L., Vaz de Melo, P. O. S. & Faloutsos, C. Quantifying Reciprocity in Large Weighted Communication Networks. Lec. Notes Comp. Science 7302, 85–96 (2012).
Serrano, M. A., Boguna, M. & Vespignani, A. Patterns of dominant flows in the world trade web. J. Econ. Interact. Coord. 2(2), 111–124 (2007).
Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. PNAS 101(11), 3747–3752 (2004).
Maslov, S. & Sneppen, K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002).
Maslov, S., Sneppen, K. & Zaliznyak, A. Detection of topological patterns in complex networks: correlation profile of the internet. Physica A 333, 529–540 (2004).
Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 64, 026118 (2001).
Chung, F. & Lu, L. Connected Components in Random Graphs with Given Expected Degree Sequences. Ann. Comb. 6, 125–145 (2002).
Park, J. & Newman, M. E. J. Origin of degree correlations in the Internet and other networks. Phys. Rev. E 68, 026112 (2003).
Catanzaro, M., Boguna, M. & Pastor-Satorras, R. Generation of uncorrelated random scale-free networks. Phys. Rev. E 71, 027103 (2005).
Park, J. & Newman, M. E. J. The statistical mechanics of networks. Phys. Rev. E 70, 066117 (2004).
Serrano, M. A. & Boguna, M. Weighted Configuration Model. AIP Conf. Proc. 776(1), 101–107 (2005).
Serrano, M. A., Boguna, M. & Pastor-Satorras, R. Correlations in weighted networks. Phys. Rev. E 74, 055101(R) (2006).
Serrano, M. A. Rich-club vs rich-multipolarization phenomena in weighted networks. Phys. Rev. E 78, 026101 (2008).
Opsahl, T., Colizza, V., Panzarasa, P. & Ramasco, J. J. Prominence and control: The weighted rich-club effect. Phys. Rev. Lett. 101, 168702 (2008).
Garlaschelli, D. & Loffredo, M. I. Generalized Bose-Fermi Statistics and Structural Correlations in Weighted Networks. Phys. Rev. Lett. 102, 038701 (2009).
Roberts, E. S. & Coolen, A. C. C. Unbiased degree-preserving randomization of directed binary networks. Phys. Rev. E 85, 046103 (2012).
Garlaschelli, D. The weighted random graph model. New. J. Phys. 11, 073005 (2009).
Snijders, T. A. B., Pattison, P. E., Robins, G. L. & Handcock, M. S. New specifications for exponential random graph models. Sociological Methodology 36(1), 99–153 (2006).
Robins, G., Pattison, P., Kalish, Y. & Lusher, D. An introduction to exponential random graph (p*) models for social networks. Social Networks 29(2), 173191 (2007).
Robins, G., Pattison, P. & Wasserman, S. Logit models and logistic regressions for social networks: III. Valued relations. Psychometrika 64(3), 371–394 (1999).
UCINET IV Datasets: http://vlado.fmf.uni-lj.si/pub/networks/data/ucinet/ucidata.htm (accessed: March 2012).
Killworth, P. D. & Bernard, H. R. Informant accuracy in social network data. Human Organization 35, 269–386 (1976).
Killworth, P. D. & Bernard, H. R. Informant accuracy in social network data II. Human Communication Research 4, 3–18 (1977).
Killworth, P. D. & Bernard, H. R. Informant accuracy in social network data III: A comparison of triadic structure in behavioral and cognitive data. Social Networks 2, 19–46 (1979).
Killworth, P. D., Bernard, H. R. & Sailer, L. Informant accuracy in social network data IV: a comparison of clique-level structure in behavioral and cognitive network data. Social Networks 2, 191–218 (1979).
Killworth, P. D., Bernard, H. R. & Sailer, L. Informant accuracy in social-network data V. An experimental attempt to predict actual communication from recall data. Social Science Research 11, 30–66 (1982).
Romney, A. K. & Weller, S. C. Predicting informant accuracy from patterns of recall among individuals. Social Networks 6, 59–77 (1984).
Gleditsch, K. S. Expanded Trade and GDP Data. J. Conflict Resol. 46(5), 712–724 (2002).
De Masi, G., Iori, G. & Caldarelli, G. A fitness model for the Italian Interbank Money Market. Phys. Rev. E 74, 066112 (2006).
Oshio, K. et al. Database of Synaptic Connectivity of C. elegans for Computation. Tech Rep CCeP, Keio Future, Keio University 3 (2003).
Pajek datasets: http://vlado.fmf.uni-lj.si/pub/networks/data/bio/foodweb/foodweb.htm (accessed: March 2012).
Feenstra, R. C. Advanced international trade: theory and evidence. Princeton University Press (Princeton, New Jersey) (2003).
Fortunato, S. Community detection in graphs. Phys. Rep. 486, 75–174 (2010).
Krivitsky, P. N. Exponential-family random graph models for valued networks. Electronic Journal of Statistics. 6(21), 1100–1128 (2012).
Desmarais, B. A. & Cranmer, S. J. Statistical inference for valued-edge networks: the generalized exponential random graph model. PLoS ONE 7(1): e30136. 10.1371/journal.pone.0030136 (2012).
Acknowledgements
The authors thank Rossana Mastrandrea for a careful reading of the manuscript. D. G. acknowledges support from the Dutch Econophysics Foundation (Stichting Econophysics, Leiden, the Netherlands) with funds from beneficiaries of Duyfken Trading Knowledge BV, Amsterdam, the Netherlands. F. R. acknowledges support from the FESSUD project on “Financialisation, economy, society and sustainable development”, Seventh Framework Programme, EU.
Author information
Authors and Affiliations
Contributions
T.S. analysed the data and prepared figures 2, 4, 5. F.P. analysed the data and prepared figure 3. F.R. and D.G. wrote the article. D.G. planned the research and prepared figure 1. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Reciprocity of weighted networks
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Squartini, T., Picciolo, F., Ruzzenenti, F. et al. Reciprocity of weighted networks. Sci Rep 3, 2729 (2013). https://doi.org/10.1038/srep02729
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02729
This article is cited by
-
Evidence of inter-state coordination amongst state-backed information operations
Scientific Reports (2023)
-
Reciprocity in directed hypergraphs: measures, findings, and generators
Data Mining and Knowledge Discovery (2023)
-
Centrality in the macroeconomic multi-network explains the spatiotemporal distribution of country per-capita income
Applied Network Science (2023)
-
Bow-tie structures of twitter discursive communities
Scientific Reports (2022)
-
The Fitness-Corrected Block Model, or how to create maximum-entropy data-driven spatial social networks
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


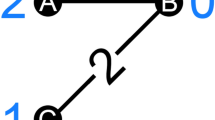

 ) and a fully non-reciprocated component (
) and a fully non-reciprocated component ( , which implies
, which implies  ).
).


