Abstract
The human finger is exquisitely sensitive in perceiving different materials, but the question remains as to what length scales are capable of being distinguished in active touch. We combine material science with psychophysics to manufacture and haptically explore a series of topographically patterned surfaces of controlled wavelength, but identical chemistry. Strain-induced surface wrinkling and subsequent templating produced 16 surfaces with wrinkle wavelengths ranging from 300 nm to 90 μm and amplitudes between 7 nm and 4.5 μm. Perceived similarities of these surfaces (and two blanks) were pairwise scaled by participants and interdistances among all stimuli were determined by individual differences scaling (INDSCAL). The tactile space thus generated and its two perceptual dimensions were directly linked to surface physical properties – the finger friction coefficient and the wrinkle wavelength. Finally, the lowest amplitude of the wrinkles so distinguished was approximately 10 nm, demonstrating that human tactile discrimination extends to the nanoscale.
Similar content being viewed by others
Introduction
Tactile perception is a subject currently enjoying great attention and rapid development, exemplified by recent articles in key journals1,2,3,4. This interest is driven by a range of factors; the development of a sense of touch in robotics, haptic perception for virtual reality and remote sensing, as well as the desire to improve the tactile aesthetics in “touch intensive” consumer products such as phones, touch-pads, paper, fabrics and conditioners. In tactile sensing, the physical finger-surface interaction is highly complex due to deformation of the finger under pressure and lateral movement5,6, combined with consideration of the surface topography7,8,9, frictional forces between finger and surface4,10 and mechanical vibrations induced by sliding1,3,11,12,13,14. The mechanical explanation of how fingerprints increase sensitivity through such microscopic force oscillations has recently been advanced1,3,15. Physiologically, the interaction of the finger with the surface is detected by mechanoreceptors embedded at various depths in the skin16, some of which are sensitive to deformation (“slow adapting receptors” for static touch) and others sensitive to vibrations arising from movement (“fast adapting receptors” for dynamic touch). The relative responses of the receptors also depend on the size of the features on the surface being probed. Ultimately, however, their signal patterns must be interpreted perceptually to allow different textures to be distinguished, compared and evaluated, which involves aspects of both neuroscience17 and psychophysics18,19.
Neurobiological studies of haptics and the skin senses are highly advanced and the roles of the various sensor cells, nerves and receptors responsible for the coding of texture, heat and pain are now increasingly understood16,18,20,21,22. The psychophysical aspects of touch, for example, the question of what physical properties are important in distinguishing surfaces and what are the perceptual limits in terms of, for example, surface feature size – have received less attention. For static touch it is established that the minimum feature size that can be detected in the absence of movement or applied vibrations is around 0.2 mm11,12. The currently accepted threshold for feature detection in dynamic touch is in the micron range21, obtained from traditional psychophysical threshold analysis on abrasive papers of varying grit size - a rather different approach to the one employed in this work. The other psychophysical studies which do exist have also predominantly been focused on unidimensional “perceived roughness”18, but multidimensional approaches have also been employed to investigate the (perceptual) dimensionality of touch19,23,24,25. The main two dimensions reported are the “rough/smooth” and “hard/soft” dimensions (especially in studies where the stimuli material properties vary greatly), with a third dimension suggested by some to be a “sticky-slippery” dimension19,23. However, direct identification of the physical property or properties, corresponding to each perceptual dimension, is still lacking. To be able to design surfaces that would generate a specific perception of the user, be it for visually impaired, safety, touch screen or consumer product applications, such a psychophysical relationship is vital and is thus the major challenge currently facing the tactile perception community. In this context, the role of friction in touch is currently the subject of much research1,2,3,5,7,9,15,26. From the tribology literature, it is clear that area of contact, surface roughness and other material properties are intimately linked to the friction coefficient4,10.
An obstacle that has thus hitherto hindered psychophysicists is the issue of manufacturing a range of chemically identical surfaces with periodic features spanning from the nanometer into the sub-millimeter size range, which are nonetheless large enough and robust enough to permit repeated interrogation with the finger. It is important that the surfaces to be researched consist of the same material since elasticity, thermal conductivity and other material specific properties contribute to haptic perception and the spatio-temporal contributors thus need to be isolated from other potential sensory discriminators. Average (physical) roughness can be controlled by polishing for example metals to different tolerances, or using a family of paper samples7,21,26, but a statistical distribution of feature heights necessarily results and no systematic periodicity can be achieved. The nanotechnology literature abounds with techniques for the manufacture of periodic features on the nanoscale27, but these techniques are generally limited to relatively small areas and are not capable of being upscaled into the micrometer regime. In this report, the challenge is overcome through the relatively inexpensive and straightforward manufacture of a series of wrinkled patterned surfaces, taking advantage of the buckling instability caused when a mechanical stress is applied to a bilayered system with higher elastic modulus of the top layer28,29,30,31. By monitoring the characteristics of the top layer, sinusoidal surface features ranging from nanometers to almost 100 micrometers could be obtained.
In this work we have employed similarity scaling on these fine textured surfaces to study how small are the structures which can be distinguished, i.e. without asking for a specific attribute to be quantified (which would otherwise focus the interrogator unnaturally on this property). A second aim was to study perceptual dimensionality and the importance of physical topography and friction in tactile discrimination of systematic fine surface textures. Wrinkled-patterned model surfaces were fabricated and used as stimuli in a multidimensional scaling experiment to systematically study the role of texture in tactile perception as well as the limitations in how small a structure can be while still being distinguishable from other structures during active exploration of a surface.
Results
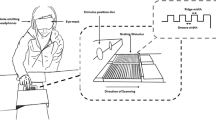
Sixteen patterned surfaces ranging in surface wavelength from 270 nm up to 90 μm, as well as two blank surfaces, were prepared in duplicate by employing surface wrinkling29,30,31 as depicted in Fig. 1. They were characterised as described in the methods section and the topographic parameters associated with the systematic, sinusoidal wrinkle pattern are shown in Table 1S. Figure 2 displays images of 4 of these surfaces, showing that essentially identical patterns are achieved at different length scales which are independent of the imaging techniques used [atomic force microscopy (AFM) for the smaller wavelengths and profilometry for the larger wavelengths]. A colour code has been used to simplify the distinction between the surfaces, from smaller (red) to larger wavelengths (blue). Blank surfaces were templated from unwrinkled polydimethylsiloxane (PDMS) specimens and thus have no systematic wrinkled topography.
Schematic diagram outlining the fabrication procedure of wrinkled surfaces.
(1) Original PDMS substrate with initial length L. (2) Stretching of the PDMS by ΔL using a strain stage. (3) Surface treatment of the PDMS either by UVO or OP treatment. (4) Spontaneous wrinkling occurrence after releasing the pre-strain. (5) Replica moulding of the wrinkled PDMS substrate onto an UV-curable adhesive.
Wrinkled-patterned surfaces ranging from nanometers to micrometers.
Representative 3D images of sinusoidal-patterned surfaces of identical material spanning two orders of magnitude in wavelength (λ) with varying amplitudes (z in this figure) fabricated by the combination of surface oxidation, surface wrinkling and replica molding techniques (Fig. 1): (a) WS2, (b) WS8, (c) WS11 and (d) WS15 (for details of surfaces included, see Table 1S). (e) An approximate colour scale for the representation of wavelengths.
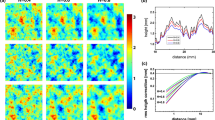
The surfaces were presented pairwise in psychophysical experiments where 20 participants (blindfolded) scaled perceived similarity of all the randomly presented pairs [201 pairs in total including test-retest comparisons (Supplementary Fig. 1S)]. The participants probed the surfaces with the index finger of their preferred hand in a designated direction (perpendicular to the grooves) for as long as they wished and at loads and speeds that they established themselves, where the average duration of one comparison was approximately 10 s. Each surface pair was assigned a self-determined similarity value on a percentage scale from completely similar (100%) to totally dissimilar (0%). The similarity values were transferred to a dissimilarity scale for each subject and submitted to mapping by individual differences scaling (INDSCAL)32,33. A two-dimensional “tactile space” was generated from the dissimilarity matrices of the individual subjects, where each pair of stimuli obtains a unique subject weight. The Cartesian distribution of the surfaces according to the resulting two perceptual dimensions for the group is shown in Fig. 3a. Despite their inherent material similarity, the different stimulus surfaces are well distributed in the perceptual map, indicating that they were confidently differentiated perceptually. The distribution of the stimuli in the map shows that surface WS1 (270 nm in wavelength) was not distinguished from the blank surfaces whereas surfaces WS2 and WS3 were (760 and 870 nm in wavelength, respectively). Moreover, the amplitude of the minimum pattern distinguished was only 13 nm, showing that the human finger with its coarse fingerprint structure in the sub-millimetre range is capable of dynamically detecting surface structures many orders of magnitude smaller. This value is much smaller than the previously reported value of 1 μm21. It is generally assumed that it is the fast adapting mechanoreceptors, i.e. the Pacinian Corpuscles that are involved in fine texture perception (surface features smaller than 100 μm). Brisben et al.34 showed that these Pacinian Corpuscles respond to vibratory amplitudes as low as 10 nm applied to the skin. The nanometre sensitivity of a finger moving over a surface suggested by Fig. 3, corresponds well to the amplitude sensitivity when a hand is mounted on a vibration table34. In this report, the vibration is provided by sequential collisions of the skin with the nanoscale structures rather than a globally homogeneous external vibration.
2D INDSCAL solution and interpretation of dimensions.
(a) Two-dimensional tactile space (for the group of the first 10 participants) based on perceived similarities among 18 surfaces; the closer the points in the map, the more similar the surfaces are perceived. (b) Finger friction coefficient versus wrinkle wavelength. Colour symbols are based on wrinkle wavelength (red is smallest and blue largest wavelengths; open symbols are “blank” reference surfaces), for details see Table 1S. The point distributions in (a) and (b) are distinctly similar, suggesting that friction and wrinkle wavelength are cues for surface similarity (a third order polynomial fits these data well). The WS1 (λ = 270 nm) surface was not perceived as different to the reference surfaces (BS1 and BS2), whereas the WS2 (λ = 760 nm) and WS3 (λ = 870 nm) surfaces were. The respective amplitudes of the latter two are 13 nm and 22 nm, respectively. The data in (b) are presented as the arithmetic mean ± s.d.
The scree-plot (depicted in Supplementary Fig. 2S and an indicator of how many dimensions the INDSCAL solution has) shows little improvement of the model fit past three dimensions (zero stress means a perfect correspondence between the similarity data and the INDSCAL configuration whereas a value of one means no fit). Although the stress values of the INDSCAL solutions indicate that both the 2D and 3D solutions represent the individual dissimilarity data matrices well, we here choose the 2D solution on the following grounds. It was supported by a principal components analysis (PCA) of the similarity matrix of the group, which resulted in only two components with eigenvalues larger than one. For the 2D INDSCAL solution, average stress over matrices was 0.332 (RSQ = 0.476), a relatively high value. It is probably caused by the unusually low and narrow range of the stimulus patterns used in this experiment combined with a relatively large between-subject variance in haptic sensitivity. The error though is random and the scale values are proportionally over- and underestimated, which is not reflected in the stress value33.
The issue of potential damage to the surfaces and thus the possibility of gradual changes in topography during the experiment has been addressed. Images of the surfaces were taken before and after the experiments and a certain amount of detritus could be observed trapped in the troughs between the peaks, while the sinusoidal pattern remained unchanged (Supplementary Fig. 4S). The surfaces were thus robust to interrogation with the fingertip. One surface was irreversibly scratched by the fingernail of participant 11 however, showing that they are not completely impervious to hard handling. In the Supplementary Information we show a comparison of the data from the first 10 and last 10 participants in Fig. 3S. The results are demonstrably very similar, but not identical so we have chosen to exclude the later participants to be sure that the slight flattening caused by the detritus does not skew the results.
The fact that the “tactile space” is well described by only two dimensions shows that the participants distinguished the surfaces with respect to two basic perceptual aspects, which cannot however, a priori be related to physical quantities. It is generally held that perceptual dimensions are not linearly related to physical quantities, or even combinations thereof. For comparison, Fig. 3b shows a plot of two of the distinguishing physical quantities of the stimulus surfaces; these are the finger friction coefficient (ordinate) and the wrinkle wavelength (abscissa). The spatial distribution of points is highly reminiscent of that in the perceptual dimension plot, suggesting that in fact the two perceptual dimensions of Fig. 3a are related to, or determined by, the two physical dimensions in Fig. 3b. Considering the different units of measurement involved the similarity is striking, but for the presence of two outliers, WS2 and WS3 (wavelengths of 760 and 870 nm, circled). This unprecedented result presumably arises from the very narrow distribution of stimuli, leading to the isolation of a limited number of perceptual outcomes. The good fit of the two tactile-space dimensions with the physical measures (wavelength and finger friction) further validate the INDSCAL and PCA solutions. Inspection of Fig. 3 reveals that the distribution of the data points along the respective curves is different, indicating that the relationship between the perceptual dimensions and the physical quantities is not a rectilinear one.
As mentioned earlier, multidimensional scaling studies report mainly “rough-smooth” and “hard-soft” perceptual dimensions19,23,24,25, with a “sticky-slippery” dimension reported as a possible third dimension23. The results obtained in the present study suggest a “rough/smooth” dimension as well as a “sticky-slippery” dimension. The reason that a “hard-soft” dimension is not observed is that we have deliberately chosen stimuli to isolate the effect of topography, so all the stimuli are equally hard. These results confirm that “sticky-slippery” is an important dimension that can be physically measured by tactile (finger) friction. It is reasonable that once the possibility to distinguish surfaces based on hardness/softness is limited, friction is used as a cue to distinguish surface feel to a higher extent (at least for fine textures where larger differences in friction are obtained).
Discussion
To further investigate the relationship between the perceptual dimensions and the implicated physical dimensions, they have been plotted against one another. Figure 4a shows how the perceptual “dimension 1” from Fig. 3a varies as a function of the corresponding finger friction coefficient of the stimuli, whereas Fig. 4b shows how “dimension 2” varies with the wavelength of their wrinkled patterns. The solid lines are guides to the eye and show very similar trends. There is clearly not a linear relationship between the perceptual dimension and the physical stimulus, but such an expectation would be unreasonable: if the perceived dimension is instead interpreted as the output from a human sensor, then the results make a great deal more sense. In general, the sensitivity of a sensor is limited to a certain range of values. As a biological example, the human eye is only capable of detecting a narrow band of electromagnetic radiation bounded by violet and red. In physics and nanotechnology, the split photodiode sensor which still forms the microlever deflection detector in the atomic force microscope displays a dependence on cantilever deflection35, which is similar to the response exemplified in Fig. 4. (In fact most linear relationships, e.g. Hooke's Law, are valid only over a certain stimulus range.) For perceptual values close to zero, an approximately linear response of the sensor to the stimulus is observed, but as the stimulus value departs from the optimum sensing regime, the sensitivity declines and the sensor response becomes “saturated” – even large changes in the stimulus remain undetectable. The sensor response is plausibly explicable in both cases of the present study.
Perceptual quantities (2D INDSCAL) compared to physical quantities.
(a) Dimension 1 vs. finger-friction coefficient and (b) Dimension 2 vs. wrinkle wavelength. Sigmoid functions fit the data well: (a) r2 = 0.96 and (b) r2 = 0.95, encircled stimuli, exclusive. The two sigmoid functions imply high sensitivity in the middle of the two perceptual ranges. The two asymptotes would indicate sensor saturation in each of the psychophysical plots (a) and (b).
In Fig. 4a, the sensitivity is determined by the loading range which can be applied (i.e., how hard the finger is pressed on the surface). An optimal friction force of about 0.4 N is employed when feeling a surface26; how hard the surface is pressed is unwittingly regulated by the finger friction coefficient. The relationship between load (L) and friction force (F) adheres to a modified Amontons' Law: F = μLn, where μ is the friction coefficient and n is an exponent (between 0.5 and 1) which accounts for the contact mechanics of the fingertip against a hard surface. Thus, it can easily be calculated what loads are required for surface probing. For example, for friction coefficients of 0.2 and 1.6 (corresponding to sensor “saturation” in this psychophysical experiment), the preferred finger loads for the participants would be about 2 N and 0.3 N, respectively (assuming n = 1). The latter value corresponds to roughly the minimum force required to maintain contact between surface and finger during sliding. At lower loads, there is not sufficient contact (or deformation) of the finger to allow the surface to be sensed at all. At the other extreme, the load corresponds to the point where the finger deformation is maximized and it is hard to slide the finger smoothly over the surface due to the resultant stick-slip phenomena36. (A lower value of n would drive the load limit to even higher values). Therefore, the psychophysical sensor is sensitive only to friction coefficients, where small changes in the load lead to significant changes in the friction force and thus the lateral deformation of the finger. This would clearly and strongly suggest that the perceptual dimension in this case is associated with the response of the slow adapting receptors16,37.
Analogous sensor saturation is observed in Fig. 4b, albeit with slightly larger scatter. The high sensitivity of Dimension 2 to wavelengths around 50 μm can again be convincingly rationalised. The human finger typically probes a surface at speeds, v, between 10 and 100 mm/s; the small areas of the templated surfaces necessitate speeds at the lower end of this range. Any given point on the finger surface will be struck by the top of a wrinkle with a frequency given by f = v/λ, where λ is the wrinkle wavelength. The optimal sensing vibration frequency, fo, of the fast adapting receptors is around 250 Hz37,38 so the arbitrary lower limit of v = 10 mm/s yields λ = 40 μm as the “excitation” wavelength. Thus, wrinkle wavelengths of the order of tens of microns are optimal for exciting vibrations to which the receptors are sensitive. As the wrinkled wavelength deviates from these values, the frequency excited becomes further from fo and the ability to distinguish textures gradually decays. The breadth of the sensing band is extended by the fact that the finger speed can also be controlled to ensure that the resulting frequency is closer to fo. This may be one reason why the data are slightly less well correlated; two physiological functions (the response of the fast acting receptors and the finger speed) may interfere perceptually.
The simple approach discussed above, while satisfactorily explaining the sensitivity, neglects the fact that the fingerprints themselves possess a sinusoidal texture which should also lead to a mechanical frequency1,3. A “beating pattern” of the two frequencies must thus occur, which is strongly dependent on the surface wavelength. In the same way that the human auditory system is sensitive to multiple frequencies simultaneously, the tactile sensing system has similar capacity for complex frequency analysis. We note that the beating pattern changes dramatically over the micrometer range which may further explain the slight scatter in this range. Irrespective of the actual physiological sensing pathways (which we have made no attempt to examine here), both the perception dimensions can be clearly related to measureable physical parameters, confirming the “sticky-slippery” and “smooth- rough” dimensions earlier identified, as well as satisfactorily explaining their physical origin.
Finally and potentially most importantly, it is observed that while the minimum pattern that could be distinguished from the unwrinkled reference surfaces had a wavelength of 760 nm, the amplitude of this pattern was only 13 nm. This shows unambiguously that the human finger, with its coarse fingerprint structure in the sub-millimeter range, is capable of dynamically detecting surface structures many orders of magnitude smaller and indicates that nanotechnology may well have a role to play in haptics and tactile perception.
Methods
The perception experiment involving measurements with human subjects was conducted according to the guidelines from the Ethical Committee for Social Science Research at Stockholm University. The subjects participated voluntarily and were given cinema tickets as compensation. Both written and oral instructions informed the subjects that they could disrupt the experiment at any time.
Surface fabrication and characterisation
Patterned surfaces were prepared by harnessing surface wrinkling28,29,30,39, as depicted in Fig. 1. Wrinkles were first formed on polydimethylsiloxane (PDMS), formed spontaneously upon applying a mechanical stress to a bilayer system where the top layer has a higher elastic modulus28,29,30,39. PDMS specimens were exposed to either ultraviolet ozone (UVO) irradiation or plasma oxidation in a pre-strained state, creating a thin stiff film with higher elastic modulus compared to the underlying softer substrate. Upon releasing the strain (like a compression) wrinkles, with the optimum wavelength minimizing the strain energy of the system, were formed spontaneously perpendicular to the direction of strain. By employing different exposure times from 1 min to 120 min, surfaces with wavelengths from 270 nm up to 90 μm were obtained. The wrinkled pattern on the PDMS was further replicated into a more durable material using the UV-curable adhesive polymer NOA81 (Norland Products Inc.) PDMS specimens with no wrinkled pattern, “blank surfaces”, were replicated as well and used as reference surfaces. The wrinkle amplitude and wavelength of the surfaces were measured with an atomic force microscope (Dimension 3100, Digital Instruments) or stylus profilometer (Taylor Hobson Form Talysurf PGI 800). In total, 16 patterned surfaces, together with two blank unpatterned reference surfaces, were used as stimuli in a psychophysical experiment as well as in tactile friction measurements.
Tactile friction measurements
The friction coefficient was measured against a human finger according to previously described protocols7,10,26 using a piezoelectric force sensor (Kistler 9251A) together with a charge amplifier (Kistler 5038A3). The wrinkled surfaces were mounted on the top plate of the force sensor with double-sided adhesive tape.
Multidimensional scaling
Twenty women (range: 21–32 years) scaled perceived similarity between all possible pairs of the 18 stimulus surfaces resulting in a total of 201 pairs including 48 duplicate pairs for test-retest reliability (Supplementary Fig. 1S). Participants were blindfolded and they probed the surfaces with the index finger of their preferred hand in a designated direction (perpendicular to the wrinkles) for as long as they wished and at loads and speeds that they established themselves. Each pair of surfaces was assigned a self-determined similarity value on a percentage scale from completely similar (100%) to totally dissimilar (0%). The similarity values were reversed to a dissimilarity scale and the set of dissimilarity matrices from 20 subjects were submitted to individual differences scaling (INDSCAL)32,33, a method for multidimensional scaling including the interindividual variance among subjects and stimuli. A two-dimensional solution was chosen from the scree-plot (Supplementary Fig. 2S) and the interpretation of these results was supported by a principal components analysis (PCA) of the similarity matrix of the group. After every comparison as well as each friction measurement, the stimulus surface was gently cleaned with acetone, using a lint-free tissue. Detailed descriptions of the surface preparation of stimuli, tactile friction measurements and the psychophysical method and data analyses are provided in the Supplementary Information.
Individual differences scaling (INDSCAL)
When conducting similarity measurements with human participants, it is inappropriate to assume they will all weight the dimensions equally. Rather, the assumption is that there is a common stimulus space to all participants, but the participants have their own way of weighting the dimensions in this space. INDSCAL is a model32 which is used to account for this unique preference for each dimension. Mathematically, the INDSCAL model can be expressed as40

where

The measured dissimilarity between stimuli j and k for subject i is expressed as  . x represents a coordinate in an r-dimensional space, i.e. xjt is the coordinate for stimulus j in dimension t. The dimensionality is denoted by r. The functions Fi are considered to be linear in metric MDS, which is the case in the present experiment. The individual differences in the use of scales are accounted for by attaching a weighting factor (w) to each dimension t for subject i. The INDSCAL program estimates both the stimuli coordinates and the individual weights in a way that
. x represents a coordinate in an r-dimensional space, i.e. xjt is the coordinate for stimulus j in dimension t. The dimensionality is denoted by r. The functions Fi are considered to be linear in metric MDS, which is the case in the present experiment. The individual differences in the use of scales are accounted for by attaching a weighting factor (w) to each dimension t for subject i. The INDSCAL program estimates both the stimuli coordinates and the individual weights in a way that  best fits the observed dissimilarity. The symbol (
best fits the observed dissimilarity. The symbol ( ) replaces the equal symbol ( = ) because equation (1) includes the unknown and uncategorized error term.
) replaces the equal symbol ( = ) because equation (1) includes the unknown and uncategorized error term.
References
Scheibert, J., Leurent, S., Prevost, A. & Debregeas, G. The role of fingerprints in the coding of tactile information probed with a biomimetic sensor. Science 323, 1503–1506 (2009).
Mate, M. C. & Carpick, R. W. A sense for touch. Nature 480, 189–190 (2011).
Wandersman, E., Candelier, R., Debrégeas, G. & Prevost, A. Texture-induced modulations of friction force: The fingerprint effect. Physical Review Letters 107, 164301 (2011).
Adams, M. J. et al. Finger pad friction and its role in grip and touch. Journal of The Royal Society Interface 10 (2013).
Childs, T. H. C. & Henson, B. Human tactile perception of screen-printed surfaces: self-report and contact mechanics experiments. Proceedings of the Institution of Mechanical Engineers Part J-Journal of Engineering Tribology 221, 427–441 (2007).
Derler, S., Gerhardt, L. C., Lenz, A., Bertaux, E. & Hadad, M. Friction of human skin against smooth and rough glass as a function of the contact pressure. Tribology International 42, 1565 (2009).
Skedung, L. et al. Finger friction measurements on coated and uncoated printing papers. Tribology Letters 37, 389–399 (2010).
Tomlinson, S. E., Lewis, R. & Carre, M. J. The effect of normal force and roughness on friction in human finger contact. Wear 267, 1311–1318 (2009).
Masen, M. A. A systems based experimental approach to tactile friction. Journal of the Mechanical Behavior of Biomedical Materials 4, 1620–1626 (2011).
Derler, S. & Gerhardt, L. C. Tribology of skin: Review and analysis of experimental results for the friction coefficient of human skin. Tribology Letters, 1–27 (2011).
Hollins, M. & Risner, S. R. Evidence for the duplex theory of tactile texture perception. Perception & Psychophysics 62, 695–705 (2000).
Bensmaia, S. J. & Hollins, M. The vibrations of texture. Somatosensory and Motor Research 20, 33–43 (2003).
Hollins, M., Bensmaia, S. J. & Washburn, S. Vibrotactile adaptation impairs discrimination of fine, but not coarse, textures. Somatosensory and Motor Research 18, 253–262 (2001).
Katz, D. The world of touch. Edited and translated by Lester E. Krueger. Hillsdale, NJ: Erlbaum (1989). (Original work published in German 1925).
Fagiani, R., Massi, F., Chatelet, E., Berthier, Y. & Akay, A. Tactile perception by friction induced vibrations. Tribology International 44, 1100–1110 (2011).
Johnson, K. O. The roles and functions of cutaneous mechanoreceptors. Current Opinion in Neurobiology 11, 455–461 (2001).
O'Doherty, J. E. et al. Active tactile exploration using a brain-machine-brain interface. Nature 479, 228–U106 (2011).
Lederman, S. J. & Klatzky, R. L. Haptic perception: A tutorial. Attention Perception & Psychophysics 71, 1439–1459 (2009).
Yoshioka, T., Bensmaia, S. J., Craig, J. C. & Hsiao, S. S. Texture perception through direct and indirect touch: An analysis of perceptual space for tactile textures in two modes of exploration. Somatosensory And Motor Research 24, 53–70 (2007).
Maricich, S. M. et al. Merkel cells are essential for light-touch responses. Science 324, 1580–1582 (2009).
Miyaoka, T., Mano, T. & Ohka, M. Mechanisms of fine-surface-texture discrimination in human tactile sensation. Journal of The Acoustical Society of America 105, 2485–2492 (1999).
Yoshioka, T., Gibb, B., Dorsch, A. K., Hsiao, S. S. & Johnson, K. O. Neural coding mechanisms underlying perceived roughness of finely textured surfaces. Journal of Neuroscience 21, 6905–6916 (2001).
Hollins, M., Bensmaia, S., Karlof, K. & Young, F. Individual differences in perceptual space for tactile textures: Evidence from multidimensional scaling. Perception & Psychophysics 62, 1534–1544 (2000).
Hollins, M., Faldowski, R., Rao, S. & Young, F. Perceptual dimensions of tactile surface texture - A multidimensional-scaling analysis. Perception & Psychophysics 54, 697–705 (1993).
Bergmann Tiest, W. M. & Kappers, A. M. L. Analysis of haptic perception of materials by multidimensional scaling and physical measurements of roughness and compressibility. Acta Psychologica 121, 1–20 (2006).
Skedung, L. et al. Tactile perception: Finger friction, surface roughness and perceived coarseness. Tribology International 44, 505–512 (2011).
Xia, Y. N., Rogers, J. A., Paul, K. E. & Whitesides, G. M. Unconventional methods for fabricating and patterning nanostructures. Chemical Reviews 99, 1823–1848 (1999).
Stafford, C. M. et al. A buckling-based metrology for measuring the elastic moduli of polymeric thin films. Nature Materials 3, 545–550 (2004).
Chung, J. Y., Youngblood, J. P. & Stafford, C. M. Anisotropic wetting on tunable micro-wrinkled surfaces. Soft Matter 3, 1163–1169 (2007).
Schweikart, A. & Fery, A. Controlled wrinkling as a novel method for the fabrication of patterned surfaces. Microchimica Acta 165, 249–263 (2009).
Chung, J. Y., Nolte, A. J. & Stafford, C. M. Surface wrinkling: A versatile platform for measuring thin-film properties. Advanced Materials 23, 349–368 (2011).
Schiffman, S. S., Young, F. W. & Reynolds, M. L. Introduction to multidimensional scaling: theory, methods and applications (Academic Press, 1981).
Borg, I. & Groenen, P. Modern multidimensional scaling: Theory and applications. (Springer Verlag New York, 1997).
Brisben, A. J., Hsiao, S. S. & Johnson, K. O. Detection of vibration transmitted through an object grasped in the hand. Journal of Neurophysiology 81, 1548–1558 (1999).
Binnig, G., Quate, C. F. & Gerber, C. Atomic Force Microscope. Physical Review Letters 56, 930–933 (1986).
Rand, C. J. & Crosby, A. J. Friction of soft elastomeric wrinkled surfaces. Journal of Applied Physics 106, 064913 (2009).
Bolanowski Jr, S. J., Gescheider, G. A., Verrillo, R. T. & Checkosky, C. M. Four channels mediate the mechanical aspects of touch. Journal of The Acoustical Society of America 84, 1680–1694 (1988).
Makous, J. C., Friedman, R. M. & Vierck, C. J. A critical band filter in touch. Journal of Neuroscience 15, 2808–2818 (1995).
Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. W. & Whitesides, G. M. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (1998).
Carroll, J. D. & Chang, J.-J. Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition. Psychometrika 35, 283–319 (1970).
Acknowledgements
We acknowledge financing from CODIRECT – the Controlled Delivery and Release Centre at YKI Institute for Surface Chemistry – financed by Vinnova and the Knowledge Foundation. M.W.R. acknowledges support from the Swedish Research Council and the Foundation for Strategic Research (SSF) through programs Biomime™ and Microstructure for Friction and Corrosion Control. B.B. acknowledges support from the EU FP6 NEST Pathfinder project MINET-Measuring the Impossible.
Author information
Authors and Affiliations
Contributions
M.W.R., B.B. and L.S. conceived the experiments. L.S. and J.Y.C. designed and fabricated the wrinkled surfaces with assistance from C.M.S. L.S. and M.A. performed the tactile similarity experiment and carried out the data analyses. M.W.R. organized the work and wrote the first draft. All authors discussed and interpreted the results and contributed to drafts of this final paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
This work is an official contribution of the National Institute of Standards and Technology (NIST); not subject to copyright in the United States. Equipment and instruments or materials are identified in the paper in order to adequately specify the experimental details. Such identification does not imply recommendation by NIST, nor does it imply the materials are necessarily the best available for the purpose.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Skedung, L., Arvidsson, M., Chung, J. et al. Feeling Small: Exploring the Tactile Perception Limits. Sci Rep 3, 2617 (2013). https://doi.org/10.1038/srep02617
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02617
This article is cited by
-
A soft magnetoelectric finger for robots’ multidirectional tactile perception in non-visual recognition environments
npj Flexible Electronics (2024)
-
A template-free, more environmentally friendly approach for glass micro-texturing
Scientific Reports (2022)
-
Normal and tangential forces combine to convey contact pressure during dynamic tactile stimulation
Scientific Reports (2022)
-
The neural mechanisms of manual dexterity
Nature Reviews Neuroscience (2021)
-
A Sticky Situation or Rough Going? Influencing Haptic Perception of Wood Coatings Through Frictional and Topographical Design
Tribology Letters (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.