Abstract
A fundamental problem in quantum information is to explore what kind of quantum correlations is responsible for successful completion of a quantum information procedure. Here we study the roles of entanglement, discord and dissonance needed for optimal quantum state discrimination when the latter is assisted with an auxiliary system. In such process, we present a more general joint unitary transformation than the existing results. The quantum entanglement between a principal qubit and an ancilla is found to be completely unnecessary, as it can be set to zero in the arbitrary case by adjusting the parameters in the general unitary without affecting the success probability. This result also shows that it is quantum dissonance that plays as a key role in assisted optimal state discrimination and not quantum entanglement. A necessary criterion for the necessity of quantum dissonance based on the linear entropy is also presented. PACS numbers: 03.65.Ta, 03.67.Mn, 42.50.Dv.
Similar content being viewed by others
Introduction
An important distinctive feature of quantum mechanics is that quantum coherent superposition can lead to quantum correlations in composite quantum systems like quantum entanglement1, Bell nonlocality2 and quantum discord3,4. Quantum entanglement has been extensively studied from various perspectives and it has served as a useful resource for demonstrating the superiority of quantum information processing. For instance, entangled quantum states are regarded as key resources for some quantum information tasks, such as teleportation, superdense coding and quantum cryptography5.
In contrast to quantum entanglement, quantum discord measures the amount of nonclassical correlations between two subsystems of a bipartite quantum system. A recent report regarding the deterministic quantum computation with one qubit (DQC1)6,7 demonstrates that a quantum algorithm to determine the trace of a unitary matrix can surpass the performance of the corresponding classical algorithm in terms of computational speedup even in the absence of quantum entanglement between the the control qubit and a completely mixed state. However, the quantum discord is never zero. This result is somewhat surprising and it has engendered much interest in quantum discord in recent years. In particular, it has led to further studies on the relation of quantum discord with other measures of correlations. Moreover, it has been shown that it is possible to formulate an operational interpretation in the context of a quantum state merging protocol8,9 where it can be regarded as the amount of entanglement generated in an activation protocol10 or in a measurement process11. Also, a unified view of quantum correlations based on the relative entropy12 introduces a new measure called quantum dissonance which can be regarded as the nonclassical correlations in which quantum entanglement has been totally excluded. For a separable state (with zero entanglement), its quantum dissonance is exactly equal to its discord.
It is always interesting to uncover non-trivial roles of nonclassical correlations in quantum information processing. The quantum algorithm in DQC1 has been widely regarded as the first example for which quantum discord, rather than quantum entanglement, plays a key role in the computational process. Moreover, a careful consideration of the natural bipartite split between the control qubit and the input state reveals that the quantum discord is nothing but the quantum dissonance of the system. This simple observation naturally leads to an interesting question: Can quantum dissonance serve as a similar key resource in some quantum information tasks? The affirmative answer was shown in an interesting piece of work by Roa, Retamal and Alid-Vaccarezza13 where the roles of entanglement, discord and dissonance needed for performing unambiguous quantum state discrimination assisted by an auxiliary qubit14,15 was studied. This protocol for assisted optimal state discrimination (AOSD) in general requires both quantum entanglement and discord. However, for the case in which there exist equal a priori probabilities, the entanglement of the state of system-ancilla qubits is absent even though its discord is nonzero and hence the unambiguous state discrimination protocol is implemented successfully only with quantum dissonance. This protocol therefore provides an example for which dissonance and not entanglement, plays as a key role in a quantum information processing task.
In this work, we show more generally that quantum entanglement is not even necessary for AOSD. Moreover, we look at the roles of correlations in the AOSD under the most general settings by considering a generic AOSD protocol. We also show that only dissonance in general is required for AOSD and quantum entanglement is never needed.
Results
The general AOSD protocol
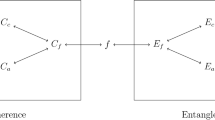
Suppose Alice and Bob share an entangled two-qubit state  (see Fig. 1), where p± ∈ [0, 1] and p+ + p− = 1, |ψ±〉 are two nonorthogonal states of the qubit of Alice (system qubit S) and {|0〉c, |1〉c} are the orthonormal bases for the one of Bob (qubit C). The reduced state of system qubit ρ = p+|ψ+〉 〈ψ+| + p−|ψ−〉〈ψ−| is a realization of the model in13 in which a qubit is prepared in the two nonorthogonal states |ψ±〉 with a priori probabilities p±. To discriminate the two states |ψ+〉 or |ψ−〉 unambiguously, the system is coupled to an auxiliary qubit A, prepared in a known initial pure state |k〉a. Under a joint unitary transformation
(see Fig. 1), where p± ∈ [0, 1] and p+ + p− = 1, |ψ±〉 are two nonorthogonal states of the qubit of Alice (system qubit S) and {|0〉c, |1〉c} are the orthonormal bases for the one of Bob (qubit C). The reduced state of system qubit ρ = p+|ψ+〉 〈ψ+| + p−|ψ−〉〈ψ−| is a realization of the model in13 in which a qubit is prepared in the two nonorthogonal states |ψ±〉 with a priori probabilities p±. To discriminate the two states |ψ+〉 or |ψ−〉 unambiguously, the system is coupled to an auxiliary qubit A, prepared in a known initial pure state |k〉a. Under a joint unitary transformation  between the system and the ancilla, one obtains
between the system and the ancilla, one obtains


where |Φ〉 = cos β|0〉 + sin βeiδ|1〉, {|0〉, |1〉} and {|0〉a, |1〉a} are the bases for the system and the ancilla, respectively. The probability amplitudes α+ and α− satisfy  , where α = 〈ψ+|ψ−〉 = |α|eiθ is the priori overlap between the two nonorthogonal states. The unitary transformation can be constructed by performing an operation
, where α = 〈ψ+|ψ−〉 = |α|eiθ is the priori overlap between the two nonorthogonal states. The unitary transformation can be constructed by performing an operation  on the original one in Ref. 13, where
on the original one in Ref. 13, where  and
and  . It has the form as
. It has the form as

where  are the components of |ψ±〉 orthogonal to
are the components of |ψ±〉 orthogonal to  and
and  , with
, with  being two arbitrary states orthogonal to the right hands of Eq. (1) and
being two arbitrary states orthogonal to the right hands of Eq. (1) and  and
and  . Obviously, only the terms with
. Obviously, only the terms with  have effect on the initial state |ψ±〉|k〉a.
have effect on the initial state |ψ±〉|k〉a.
The General AOSD Protocol Illustration.
Alice and Bob share a pure entangled state |ζ〉 of qubits S and C. To discriminate the two states |ψ+〉 or |ψ−〉 of S, Alice performs a joint unitary transformation  between qubits S and A, followed by two independent von Neumann measurements on the two qubits. Her state discrimination is successful if the outcome of A is 0, but unsuccessful if outcome 1.
between qubits S and A, followed by two independent von Neumann measurements on the two qubits. Her state discrimination is successful if the outcome of A is 0, but unsuccessful if outcome 1.
The state of the system-ancilla qubits is given by

which depends on β and δ and it is generally not equivalent to the corresponding one in13 under local unitary transformations unless |Φ〉 = |+〉. The state discrimination is successful if the ancilla collapses to |0〉a. This occurs with success probability given by

where  is the unit matrix for the system qubit. Without loss of generality, let us assume that p+ ≤ p− and denote
is the unit matrix for the system qubit. Without loss of generality, let us assume that p+ ≤ p− and denote  . The analysis of the optimal success probability can be divided into two cases: (i)
. The analysis of the optimal success probability can be divided into two cases: (i)  , Psuc is attained for
, Psuc is attained for  ; (ii)
; (ii)  , Psuc is attained for |α+| = 1 (or equivalently |α−| = |α|). One has
, Psuc is attained for |α+| = 1 (or equivalently |α−| = |α|). One has


Before proceeding further to explore the roles of correlations in the AOSD, we make the following remarks.
Remark 1
State discrimination of a subsystem in a reduced mixed state has practical interest in conclusive quantum teleportation where the resource is not prepared in a maximally entangled state (see Refs. 16,17,18). In the conclusive teleportation protocol, the sender Alice possesses an arbitrary one-qubit state |φ〉Alice = a|0〉 + b|1〉 and she shares a non-maximally entangled state |Ψ+(θ)〉 = cos θ|00〉 + sin θ|11〉 with the receiver Bob. Under the protocol, one has

where |Ψ±(θ)〉 = cos θ|00〉 ± sin θ|11〉, |Φ±(θ)〉 = sin θ|01〉 ± cos θ|10〉 and σx, σy, σz are Pauli matrices. The concurrences19 of the states |Ψ±(θ)〉 and |Φ±(θ)〉 are all equal to  . The states |Ψ±(θ)〉 are orthogonal to the states |Φ±(θ)〉, but {|Ψ+(θ)〉, |Ψ−(θ)〉} (or {|Φ+(θ)〉, |Φ−(θ)〉}) are not mutually orthogonal. To teleport the unknown state |φ〉Alice from Alice to Bob with perfect fidelity (equals to 1), state discrimination16,17,18 is generally required. It should also be noted that only the maximally entangled states (with θ = π/4) can realize the perfect teleportation with unit success probability.
. The states |Ψ±(θ)〉 are orthogonal to the states |Φ±(θ)〉, but {|Ψ+(θ)〉, |Ψ−(θ)〉} (or {|Φ+(θ)〉, |Φ−(θ)〉}) are not mutually orthogonal. To teleport the unknown state |φ〉Alice from Alice to Bob with perfect fidelity (equals to 1), state discrimination16,17,18 is generally required. It should also be noted that only the maximally entangled states (with θ = π/4) can realize the perfect teleportation with unit success probability.
Remark 2
Through quantum teleportation, we see that our model recover the scheme in13, in which the principal qubit is randomly prepared in one of the two pure states |ψ+〉 or |ψ−〉. Let us conisder replacing the entangled resource |Ψ+(θ)〉 by maximally entangled states randomly prepared with a probabilities as { ,
,  ,
,  ,
,  }. Although they are all maximally entangled states and each of them is a resource for perfect teleportation, perfectly faithful teleportation cannot be realized in this case. It can be shown that the fidelity of teleportation is the one corresponding to the average state16
}. Although they are all maximally entangled states and each of them is a resource for perfect teleportation, perfectly faithful teleportation cannot be realized in this case. It can be shown that the fidelity of teleportation is the one corresponding to the average state16

Consequently, the amount of entanglement contributing to teleportation is not just the average value of the entanglement which is  , but the entanglement of the average state as
, but the entanglement of the average state as  . Therefore the amount of entanglement available depends crucially on the knowledge of the entangled state. The amount of quantum entanglement that is needed for the AOSD scheme considered here, as well as the one in Ref. 13, refers to the entanglement of the average state,
. Therefore the amount of entanglement available depends crucially on the knowledge of the entangled state. The amount of quantum entanglement that is needed for the AOSD scheme considered here, as well as the one in Ref. 13, refers to the entanglement of the average state,  and not to the average value of the entanglement as
and not to the average value of the entanglement as  .
.
We are now ready to investigate the roles of correlations in the AOSD. To this end, let us first calculate the concurrence of ρSA:

with  . When β = π/4 and δ = 0, Eq. (5) reverts to the result in13.
. When β = π/4 and δ = 0, Eq. (5) reverts to the result in13.
Let us impose the constraint  for any α, α+ and p+. It is then easy to see that
for any α, α+ and p+. It is then easy to see that

Based on Eq. (6), state (2) is a separable state as

where |η1〉 and |η2〉a are two unnormalized states as

where  .
.
Note that the state (2) has rank two and it is really the reduced state of the following tripartite pure state

Its discord can be derived analytically as D(ρSA) = S(ρA) − S(ρSA) + E(ρSC) = S(ρA) − S(ρC) + E (ρSC) using the Koashi-Winter identity20, where S(ρ) is the von Neumann entropy, E(ρSC) is the entanglement of formation19 between the principal system and the qubit C. The explicit expression for the discord is

where  , τA is the tangle between A and SC, τC is the tangle between C and SA and
, τA is the tangle between A and SC, τC is the tangle between C and SA and  is the concurrence between S and C in the state ρSC. One can obtains
is the concurrence between S and C in the state ρSC. One can obtains



with τS the tangle between S and AC,  and τ(|Ψ〉) the three-tangle21. The tangle between S and AC is given by
and τ(|Ψ〉) the three-tangle21. The tangle between S and AC is given by

and the three-tangle is

Dissonance for cases (i) and (ii)
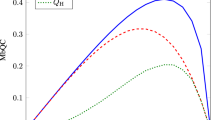
For case (i), upon the substitution  , p− = 1 − p+ and Eqs. (6)(11)(12)(13) into Eq. (10), one has the analytical expression for the dissonance, which depends only on |α| and p+. In Fig. 2, we plot the curves of the dissonance versus |α| for p+ = 1/2, 1/4, 1/8, respectively (see the curves with D(ρSA) > 0). For case (ii), because |α+| = 1, one has β = π/2 and the state ρSA is
, p− = 1 − p+ and Eqs. (6)(11)(12)(13) into Eq. (10), one has the analytical expression for the dissonance, which depends only on |α| and p+. In Fig. 2, we plot the curves of the dissonance versus |α| for p+ = 1/2, 1/4, 1/8, respectively (see the curves with D(ρSA) > 0). For case (ii), because |α+| = 1, one has β = π/2 and the state ρSA is

with ρa = p+|1〉a〈1| + p−|μ〉a〈μ|,  . The state (14) is clearly a direct-product state hence its dissonance is zero. In Fig. 2, for case (ii), we also plot the curves of dissonance versus |α| for the same p+'s (see the curves with D(ρSA) = 0). Fig. 2 shows that dissonance is a key ingredient for AOSD other than entanglement for case (i) and that the classical state can accomplish the task of AOSD for case (ii).
. The state (14) is clearly a direct-product state hence its dissonance is zero. In Fig. 2, for case (ii), we also plot the curves of dissonance versus |α| for the same p+'s (see the curves with D(ρSA) = 0). Fig. 2 shows that dissonance is a key ingredient for AOSD other than entanglement for case (i) and that the classical state can accomplish the task of AOSD for case (ii).
Geometric picture
It can be observed that the optimal success probability Psuc,max in Eq. (4) can be analyzed in two different regions:  and
and  . Here based on the positive-operator-valued measure (POVM) strategy15, we provide a geometric picture of Psuc,max. Since the success probability, the concurrence and the discord of state ρSA under the constraints in Eq. (6) are all independent of the phase θ of α, one can simply set θ = 0 and regard the states |ψ±〉 as two unit vectors in
. Here based on the positive-operator-valued measure (POVM) strategy15, we provide a geometric picture of Psuc,max. Since the success probability, the concurrence and the discord of state ρSA under the constraints in Eq. (6) are all independent of the phase θ of α, one can simply set θ = 0 and regard the states |ψ±〉 as two unit vectors in  with the angle γ = arccos |α| between them. The square roots of the a priori probabilities, i.e.,
with the angle γ = arccos |α| between them. The square roots of the a priori probabilities, i.e.,  and
and  , behave like wave amplitudes and the effects of the coherence can be seen from the states |ζ〉 and |Ψ〉. In Fig. 3, we plot two vectors
, behave like wave amplitudes and the effects of the coherence can be seen from the states |ζ〉 and |Ψ〉. In Fig. 3, we plot two vectors  and
and  with
with  to denote
to denote  and
and  , respectively. The two POVM elements that identify the states
, respectively. The two POVM elements that identify the states  can be implemented as
can be implemented as  , with r± ≥ 0. The vectors
, with r± ≥ 0. The vectors  and
and  correspond to the unnormalized states
correspond to the unnormalized states  with the coefficients
with the coefficients  . The third POVM element giving the inconclusive result is
. The third POVM element giving the inconclusive result is  . The elements Π±,0 are required to be positive - this is a constraint on the POVM strategy. Finally, the probability of successful discrimination is PPOVM = (r+p+ + r−p−)(1 − |α|2), which is
. The elements Π±,0 are required to be positive - this is a constraint on the POVM strategy. Finally, the probability of successful discrimination is PPOVM = (r+p+ + r−p−)(1 − |α|2), which is

When  , the optimal PPOVM is attained at
, the optimal PPOVM is attained at  . The vectors
. The vectors  and
and  , where E is the intersection point of AE and BE (see Fig. 3). The maximum value of PPOVM is the square of |AB|, nanmely
, where E is the intersection point of AE and BE (see Fig. 3). The maximum value of PPOVM is the square of |AB|, nanmely  , which recovers Eq. (4a). When
, which recovers Eq. (4a). When  , the point E coincides with B for p+ < p− (or A for p+ > p−), for the optimal PPOVM one has r− = 1 (or r+ = 1) and PPOVM = p−(1 − |α|2). For
, the point E coincides with B for p+ < p− (or A for p+ > p−), for the optimal PPOVM one has r− = 1 (or r+ = 1) and PPOVM = p−(1 − |α|2). For  and p+ < p−, E lies outside of the angle
and p+ < p−, E lies outside of the angle  and
and  is opposite to
is opposite to  . Consequently, we do not get a physically realizable value of r+. The optimal PPOVM strategy then occurs at r− = 1 and r+ = 0 (i.e., E coincides with B), one has
. Consequently, we do not get a physically realizable value of r+. The optimal PPOVM strategy then occurs at r− = 1 and r+ = 0 (i.e., E coincides with B), one has  , which is Eq. (4b).
, which is Eq. (4b).
Discussion
In summary, based on a sufficiently general AOSD protocol, we found that the entanglement between the principal qubit and the ancilla is completely unnecessary. Moreover, this quantum entanglement can be arbitrarily zero by adjusting the parameters in the joint unitary transformation without affecting the success probability. Theoretically, this fact clearly indicates that dissonance plays a key role in assisted optimal state discrimination other than entanglement. Experimentally, the absence of entanglement can be more easily observed because there is no restriction on the a priori probabilities. In Fig. 4, we present a realization of the unitary transformation  in Eq. (1) for the initial states |ψ+〉 = |0〉,
in Eq. (1) for the initial states |ψ+〉 = |0〉,  and |k〉a = |0〉a by using single-qubit gates and two-qubit controlled-unitary gates. These gates can be demonstrated experimentally in many systems23,24 in recent years. The success probability of state discrimination is determined by steps (i) to (iii), which transform the system-ancilla state into
and |k〉a = |0〉a by using single-qubit gates and two-qubit controlled-unitary gates. These gates can be demonstrated experimentally in many systems23,24 in recent years. The success probability of state discrimination is determined by steps (i) to (iii), which transform the system-ancilla state into


It is not affected by the controlled-UΦ in step (iv), which can adjust the correlations in state (2).
Realization of the General Unitary Transformation.
For the initial states |ψ+〉 = |0〉,  and |k〉a = |0〉a, the unitary transformation
and |k〉a = |0〉a, the unitary transformation  in Eq. (1) can be realized in four steps: (i) controlled-UA with the system S being the control qubit; (ii) controlled-US where the system S is controlled by the ancilla A; (iii) local unitary VA on the auxiliary qubit; (iv) controlled-UΦ with the same control qubit and target as the second step. The single qubit operations
in Eq. (1) can be realized in four steps: (i) controlled-UA with the system S being the control qubit; (ii) controlled-US where the system S is controlled by the ancilla A; (iii) local unitary VA on the auxiliary qubit; (iv) controlled-UΦ with the same control qubit and target as the second step. The single qubit operations  ,
,  ,
,  and
and  , with
, with  ,
,  and
and  . Here, the states with a bar,
. Here, the states with a bar,  ,
,  and
and  , denote (iσy,a|ϕA〉a)*, (−iσy|ϕS〉)* and (iσy,a|ϕV〉a)*.
, denote (iσy,a|ϕA〉a)*, (−iσy|ϕS〉)* and (iσy,a|ϕV〉a)*.
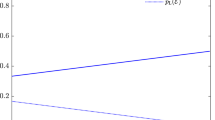
Let us also reiterate a necessary criterion for the requirement of dissonance in AOSD based on linear entropy. Under the general protocol, Alice and Bob share the entangled state |ζ〉, encoded in the basis of the polarization of the qubit, Bob can acquire knowledge of the linear entropy  of Alice's qubit. If
of Alice's qubit. If  , he can be sure that Alice needs dissonance for her AOSD (see Fig. 5). Finally, we would like to mention that local distinguishability of multipartite orthogonal quantum states was studied in Ref. 22 where again the local discrimination of entangled states does not require any entanglement.
, he can be sure that Alice needs dissonance for her AOSD (see Fig. 5). Finally, we would like to mention that local distinguishability of multipartite orthogonal quantum states was studied in Ref. 22 where again the local discrimination of entangled states does not require any entanglement.
Necessary criterion for requiring dissonance in AOSD based on linear entropy or purity.
The linear entropy reads  and the purity
and the purity  . For a given amount of |α|, when
. For a given amount of |α|, when  , the dissonance for the AOSD is zero (see the region below the dashed line). we note that
, the dissonance for the AOSD is zero (see the region below the dashed line). we note that  when
when  . This means that if
. This means that if  , then the dissonance is necessarily needed for the AOSD.
, then the dissonance is necessarily needed for the AOSD.
References
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Physics (Long Island City, N.Y.) 1, 195–200 (1964).
Ollivier, H. & Zurek, W. H. Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Henderson, L. & Vedral, V. Classical, quantum and total correlations. J. Phys. A 34, 6899–6905 (2001).
Ekert, A. K. Quantum cryptography based on Bell's theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Lanyon, B. P., Barbieri, M., Almeida, M. P. & White, A. G. Experimental quantum computing without entanglement. Phys. Rev. Lett. 101, 200501 (2008).
Datta, A., Shaji, A. & Caves, C. M. Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008).
Cavalcanti, D. et al. Operational interpretations of quantum discord. Phys. Rev. A 83, 032324 (2011).
Madhok, V. & Datta, A. Interpreting quantum discord through quantum state merging. Phys. Rev. A 83, 032323 (2011).
Piani, M. et al. All nonclassical correlations can be activated into distillable entanglement. Phys. Rev. Lett. 106, 220403 (2011).
Streltsov, A., Kampermann, H. & Bruß, D. Linking quantum discord to entanglement in a measurement. Phys. Rev. Lett. 106, 160401 (2011).
Modi, K., Paterek, T., Son, W., Vedral, V. & Williamson, M. Unified view of quantum and classical correlations. Phys. Rev. Lett. 104, 080501 (2010).
Roa, L., Retamal, J. C. & Alid-Vaccarezza, M. Dissonance is required for assisted optimal state discrimination. Phys. Rev. Lett. 107, 080401 (2011).
Neumann, J. V. Mathematical Foundations of Quantum Mechanics Vol. 2, (Princeton University Press 1996).
Jafarizadeh, M. A., Rezaei, M., Karimi, N. & Amiri, A. R. Optimal unambiguous discrimination of quantum states. Phys. Rev. A 77, 042314 (2008).
Horodecki, M., Horodecki, P. & Horodecki, R. General teleportation channel, singlet fraction and quasidistillation. Phys. Rev. A 60, 1888–1898 (1999).
Roa, L., Delgado, A. & Fuentes-Guridi, I. Optimal conclusive teleportation of quantum states. Phys. Rev. A 68, 022310 (2003).
Kim, H., Cheong, Y. W. & Lee, H. W. Generalized measurement and conclusive teleportation with nonmaximal entanglement. Phys. Rev. A 70, 012309 (2004).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998).
Koashi, M. & Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 69, 022309 (2004).
Coffman, V., Kundu, J. & Wootters, W. K. Distributed entanglement. Phys. Rev. A 61, 052306 (2000).
Walgate, J., Short, A. J., Hardy, L. & Vedral, V. Local distinguishability of multipartite orthogonal quantum states. Phys. Rev. Lett. 85, 4972–4975 (2000).
Chow, J. M. et al. Universal quantum gate set approaching fault-tolerant thresholds with superconducting qubits. Phys. Rev. Lett. 109, 060501 (2012).
Brunner, R. et al. Two-qubit gate of combined single-spin rotation and interdot spin exchange in a double quantum dot. Phys. Rev. Lett. 107, 146801 (2011).
Acknowledgements
F.L.Z. is supported by NSF of China (Grant No. 11105097). J.L.C. is supported by National Basic Research Program (973 Program) of China under Grant No. 2012CB921900, NSF of China (Grant Nos. 10975075 and 11175089) and partly supported by National Research Foundation and Ministry of Education of Singapore.
Author information
Authors and Affiliations
Contributions
F.L.Z and J.L.C. initiated the idea. F.L.Z. derived the formulas and prepared the figures. J.L.C., F.L.Z., L.C.K. and V.V. wrote the main manuscript text. All authors contributed to the derivation and the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Zhang, FL., Chen, JL., Kwek, L. et al. Requirement of Dissonance in Assisted Optimal State Discrimination. Sci Rep 3, 2134 (2013). https://doi.org/10.1038/srep02134
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02134
This article is cited by
-
Sequential state discrimination with quantum correlation
Quantum Information Processing (2018)
-
Universal quantum correlation close to quantum critical phenomena
Scientific Reports (2016)
-
Local quantum uncertainty in two-qubit separable states: a case study
Quantum Information Processing (2016)
-
Linear monogamy of entanglement in three-qubit systems
Scientific Reports (2015)
-
Reconstruction of bipartite states via unambiguous state discrimination and mutually unbiased measurement
Quantum Information Processing (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 .
.
 ,
,  , the angle γ = arccos |α| and AC
, the angle γ = arccos |α| and AC  , the point E locates inside of the angle
, the point E locates inside of the angle  ; for
; for  , the point E coincides with the point B for p+ < p− (or A for p+ > p−).
, the point E coincides with the point B for p+ < p− (or A for p+ > p−).
