Abstract
Colloidal clusters are an unusual state of matter where tunable interactions enable a sufficient reduction in their degrees of freedom that their energy landscapes can become tractable — they form a playground for statistical mechanics and promise unprecedented control of structure on the submicron lengthscale. We study colloidal clusters in a system where a short-ranged polymer-induced attraction drives clustering, while a weak, long-ranged electrostatic repulsion prevents extensive aggregation. We compare experimental yields of cluster structures with theory which assumes simple addition of competing isotropic interactions between the colloids. Here we show that for clusters of size 4 ≤ m ≤ 7, the yield of minimum energy clusters is much less than expected. We attribute this to an anisotropic self-organized surface charge distribution which leads to unexpected kinetic trapping. We introduce a model for the coupling between counterions and binding sites on the colloid surface with which we interpret our findings.
Similar content being viewed by others
Introduction
Colloidal clusters are important for at least four reasons. Firstly, like atomic clusters, their restricted degrees of freedom lead to tractable energy landscapes which in the case of colloids may be directly measured in real space at the single-particle level1,2,3,4. Cluster transitions and reactions form a new kind of “supra-colloidal chemistry”3,5. The second reason colloidal clusters are important is that their self-assembly from monomers is very similar to that of nanoparticles. Although crucial to a variety of nanotechnologies6, self-assembly often fails to produce the desired structure and the mechanism of failure can be hard to elucidate at the nanoscale. Insight gained from direct visualisation of colloids can help resolve such barriers to assembly. Thirdly, colloidal clusters are an important system in their own right, with the promise of materials with new optical properties7,8,9 and novel phases, some of which provide insight into protein aggregation and clustering10,11,12,13,14. Finally, colloids (particularly charged colloids) can be regarded as a model of biological components such as proteins, whose self-assembly is important for our basic understanding of self-organization of biomatter.
To fully exploit the potential of colloidal clusters and “molecules”, it is necessary to understand their behaviour and in particular to establish ways to optimize yields of desired structures15. Perhaps the simplest cluster-forming system is built around a spherically symmetric attraction which may be realized by adding non-adsorbing polymer to a colloidal suspension. Here long-ranged electrostatic repulsions prevent the formation of large aggregates11. Such systems present a familiar problem of needing to tackle multiple length- and time-scales. In this case the degrees of freedom of the small ions are integrated out and electrostatic interactions are treated with a (spherically symmetric) Yukawa potential. Those of the polymer molecules are also treated with a one-component description16 which leads to an effective attraction between the colloids known as the Asakura-Oosawa (AO) potential, whose strength is approximately proportional to the polymer concentration cp. These repulsive and attractive components are then summed to give an effective interaction (Fig. 1a). This cornerstone of soft matter physics has been remarkably successful17.
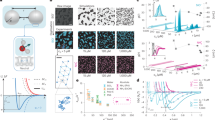
Characterization of interparticle interactions and cluster formation.
(a), Various potentials: Morse (black line) denotes a Morse potential for a well depth 4.6 kBT and range parameter ρ0 = 33.1. AO (red dashed line) denotes Asakura-Oosawa for cp = 6.02 × 10−4, YUK (light cyan line) denotes a Yukawa interaction for a contact potential of kBT and inverse Debye screening length κσ = 0.5. AO + YUK (blue dotted line) sums AO and YUK illustrates a treatment of the electrostatic repulsions as a small perturbation (see text). DZUG is the Dzugutov potential. (b), Determining the repulsive interactions between the clusters. Experimental g(r) for cp = 6.02 × 10−4 (circles) and MC simulation (solid line) treating clusters as single particles, each with a charge Z = 61. (c), Confocal micrograph of clusters formed at cp = 1.43 × 10−3. Bar is 10 μm.
However it was recently shown that non-trivial correlation effects sometimes play an important role in electrostatic interactions between charged colloids (see, e.g., Refs. 18,19,20,21). Unlike the rather-well studied situation of systems with purely electrostatic interactions, here we probe in detail the situation where like-charged particles are forced to approach by depletion-induced attraction. We show for a popular model system that the simple one-component description fails qualitatively under such a frustrated situation, which leads to novel kinetic trapping of colloidal cluster configurations. In our system, the polymer-mediated AO attraction is similar to the Morse potential (Fig. 1a). This has a single nondegenerate structure for a minimum energy cluster of given size22. For our parameters, these ground state structures are unaltered by the addition of a weak-long-ranged Yukawa repulsion23,24. Under the assumptions of treating the system at the one-component colloid level, we therefore expect an increase in the population of these minimum energy clusters as the polymer concentration cp is increased. As we shall see, even in our simple model system, the behaviour is not as straightforward as one might expect, because of non-trivial coupling between complex degrees of freedom.
Results
Determination of parameters
Our experimental system is illustrated by the confocal microscopy image in Fig. 1c. Details of the polymethyl methacrylate (PMMA) colloids and apolar solvent used are given in Methods. We determine the coordinates of each particle using confocal microscopy. We identify cluster structures shown in Fig. 2b from coordinate data with reference to the bond network in each cluster. As described in Supplementary Information, for m = 3, 4 clusters, the number of bonds is sufficient to discriminate between different cluster shapes. For larger clusters, we use the topological cluster classification25,26. The large separations between the clusters indicate they carry some electrostatic charge, while the clustering is driven by the addition of polymer. While we have previously determined the interactions between the colloids induced by the polymer27, here we need to estimate the electrostatic charge. We proceed as follows. The clusters are treated as individual particles and their different sizes neglected28. The cluster size distribution is shown in Fig. 2a for a polymer weight fraction cp = 6.02 × 10−4: the mean <m> = 3.3 and standard deviation is 4.4. In Fig. 1b, we fit the radial distribution function g(r) with Monte Carlo simulation according to a Yukawa potential29, yielding Z = 61 ± 20 charges per cluster and a Debye screening length of κ−1 = 2.0 ± 0.4σ. This suggests around 10–20 charges per colloid, which corresponds to a Yukawa potential at contact of βεYUK = Z2λB/[(1 + κσ/2)2σ] ~ 1–3 where β = 1/kBT (kB is Boltzmann's constant) and λB ≈ 25 nm is the Bjerrum length. Although this charge is very low, the value is close to measurements on PMMA colloids in solvents of similar dielectric constant30. Simulations using these parameters for a Yukawa repulsion and Morse potential to mimic the addition of polymer indicate that each cluster may be treated separately, i.e. that cluster-cluster interactions may be neglected31.
Characterization of cluster formation.
(a), Cluster size distribution for cp = 6.02 × 10−4. (b), “Structural yield” Nc/Nm as a function of cp × 10−3 for 3A, 4D, 4A, 5A, 6Z, 7A clusters (see structures depicted). 6A is also shown. Only in the case of m = 3 does the yield of the global energy minimum (3A) approach 100%. Vertical dashed line denotes the polymer overlap concentration. βεAO is the contact potential for the AO interaction.
Isolated clusters as separate systems
We therefore proceed to consider the behaviour of the individual clusters as isolated systems. Figure 2b shows the “structural yield” Nc/Nm as a function of the attractive interaction cp. Nc is the number of clusters of a given structure and Nm is the total number of clusters containing m colloids. For the smaller cluster sizes (m ≤ 5) a greater proportion are found in the minimum energy clusters for the Morse potential (denoted as the number of particles in the cluster and the letter “A”) upon increasing cp. In the case of m = 6, we do not find the minimum energy octahedal 6A cluster22. We illustrate the clusters identified in Fig. 2. Considering the topology of the 3A, 4A, 5A and 6A clusters we see that the distance between all the nearest neighbours will be the same due to the short range AO potential and next nearest neighbours do not contribute, if we ignore the weak electrostatic repulsion. The minimum energy for these clusters is thus approximately proportional to the number of nearest neighbours or contacts. For m = 6, the global minimum structure for the Dzugutov potential32, “6Z” has a polytetrahedral C2v point group symmetry and the same number of contacts as the 6A octahedron. 6Z is illustrated in Fig. 2b. Here we note that this Duzgutov potential has a repulsive “hump” [u(r) > 0] at a longer range than the attractive well and thus our system might be qualitatively similar due to the competing interactions. However as shown in Fig. 1a, the hump in the Dzugutov potential is very much more pronounced than would be expected by assuming simple addition of Morse/AO and Yukawa contributions.
Neglecting the weak charge, both 6A and 6Z clusters have a very similar ground state potential energy but there are other contributions to the cluster's free energy: configurational entropy and electrostatic energy. The latter suggests that 6Z should be 24 times as popular as 6A2. Moreover, 6Z is further favoured by its larger radius of gyration, which lowers electrostatic energy33. However, we do not find 6A at all, which is suggestive of a further mechanism at play: the kinetic pathway and the associated energy barrier. Addition of particles leads to the sequence 3A → 4A → 5A → 6Z, while the formation of 6A requires a bond to be broken and insertion of a particle to form the 4-membered square ring.
We expect an increase of polymer concentration (lowering of the effective temperature) to promote clusters which maximize the number of bonds, i.e. 3–7A, or 6Z. This we see in Fig. 2b for m = 3, in the near 100% yield of 3A triangles at high cp. In Fig. 3a we show the distribution of the bond angle γ in m = 3 at different polymer concentrations. In addition to an increasing 3A triangle population at higher cp, we find a considerable number of clusters with a large bond angle, indicating an elongated structure. In the case of more complex clusters, such as 7A, an initial increase in yield with cp is followed by a decrease, presumably due to frustration, at high interaction strength [Fig. 2b].
Classification of the type of clusters made of three and four particles.
(a), Distribution of bond angle γ for m = 3 clusters. As cp (listed ×10−3) is increased, almost all clusters are 3A triangles. (b), Maximum centre separation, d, for m = 4 at cp = 7.1 × 10−4. Blue dashed line denotes 4A tetrahedron, pink (solid) line 4D diamond and orange (solid) line (“4×”) with fewer bonds. (c), Distribution of angle α as described in the text and indicated for 4A and 4D clusters. The schematic insets show a fourth particle to emphasise that the cluster is pictured along the axis of two touching colloids. As cp (listed ×10−3) is increased substantially, the population of 4D diamonds remains significant.
However, intermediate cluster sizes, 4 ≤ m ≤ 6 show a most surprising behaviour. We focus on m = 4 because larger clusters form by addition to 4-membered clusters. One expects that upon increasing the polymer concentration, more clusters should be found in the 4A tetrahedron ground state. However, after an initial rise to a value of N4A/N4 ≈ 0.2, the population of tetrahedra shows no further increase for higher polymer concentration. Motivated by our analysis of m = 3 clusters, we consider structures in addition to the 4A tetrahedron.
We measure the largest separation of two colloid centres d in 4-membered clusters. Now d ≈ σ for 4A tetrahedra, while the maximum value is d ≈ 3σ for a line of 4 particles. We choose this order parameter because a single value is sufficient to distinguish three structures in the m = 4 population: the 4A tetrahedra (6 bonds), a diamond-shaped structure we term 4D (5 bonds) and clusters with a fewer bonds which we denote 4×. These 4× have either 4 bonds (squares with  ) or 3 bonds (lines). Their populations are shown in Fig. 3b for a polymer concentration of cp = 7.1 × 10−4. We find that the 4D diamond is the most popular 4-membered cluster. Unlike more complex (e.g. 7A) clusters1, for m = 4, there is no geometric frustration in the formation of tetrahedra. In contrast with these experiments, as shown in Fig. S2 in Supplementary Information, Brownian dynamics simulations of four particles interacting via the Morse and Yukawa potentials parameterised to our experimental values show a clear peak in the 4D population at intermediate attraction (polymer concentration) and a 100% yield of tetrahedra at strong interaction strength. Similarly, for m = 5 and m = 6, at sufficient attraction, simulations find a high population of 5A triangular bipyramids and 6Z polytetrahedra24. In the case of m = 4, by measuring the angle subtended by the two particles with the largest separation about the axis of the two remaining particles, it is possible to draw analogy to the m = 3 case. This angle α is indicated in Fig. 3c for 4A tetrahedra and 4D diamonds. In Fig. 3c we plot the same state points as in Fig. 3a. The difference is striking between the two figures, indicating a considerable number of particles remaining in the 4D state even at the highest polymer concentrations considered.
) or 3 bonds (lines). Their populations are shown in Fig. 3b for a polymer concentration of cp = 7.1 × 10−4. We find that the 4D diamond is the most popular 4-membered cluster. Unlike more complex (e.g. 7A) clusters1, for m = 4, there is no geometric frustration in the formation of tetrahedra. In contrast with these experiments, as shown in Fig. S2 in Supplementary Information, Brownian dynamics simulations of four particles interacting via the Morse and Yukawa potentials parameterised to our experimental values show a clear peak in the 4D population at intermediate attraction (polymer concentration) and a 100% yield of tetrahedra at strong interaction strength. Similarly, for m = 5 and m = 6, at sufficient attraction, simulations find a high population of 5A triangular bipyramids and 6Z polytetrahedra24. In the case of m = 4, by measuring the angle subtended by the two particles with the largest separation about the axis of the two remaining particles, it is possible to draw analogy to the m = 3 case. This angle α is indicated in Fig. 3c for 4A tetrahedra and 4D diamonds. In Fig. 3c we plot the same state points as in Fig. 3a. The difference is striking between the two figures, indicating a considerable number of particles remaining in the 4D state even at the highest polymer concentrations considered.
Discussion
Why then do the experiments have such a low number of ground state structures and a high 4D population? One argument might be that the AO model is starting to break down as we exceed the polymer overlap concentration, which occurs at cp ≈ 8.5 × 10−4 as indicated in Fig. 2b, but for our parameters this effect is slight34. We also note that clustering behaviour solely induced by depletion interactions in a similar system can be well described by simulations based on the Morse potential26, which excludes any possibility that kinetic trapping is caused by unknown short-range attractions which prevent smooth rotation of particles. Another possibility is that the counterion entropy acts to stablise the 4D clusters, as these are less compact than 4A. This may hold for aqueous systems where the ionic strength is higher than is the case here and the transition to more compact clusters significantly reduces the space available to the counterions, as they are bound to a region of order a Debye length from the colloids35. However, here the number of ions is very small and the Debye length is so large (~ 2σ) that the relative change in volume accessible to the ions in the 4D → 4A transition is so small that this mechanism has a rather limited contribution (somewhat less than kBT for our parameters). Although this mechanism helps stabilisation of 4D structures, it is not enough to explain our observation. Thus, we postulate that 4D is stabilized by the weak charging present in this system. Furthermore, the surface charges, unlike the spherically symmetric distribution assumed in a one-component description, may in fact be nonuniformly distributed on the colloid surfaces, leading to anisotropic electrostatic interactions36,37. As shown later, we argue that this is a consequence of a coupling between the charge distribution on colloid surfaces and the spatial arrangement of particles in a cluster.
First we consider the effects of weak charging, which enhances the formation of 4D clusters. 4D and 4A clusters are formed by an attachment of one particle to 3A. For 3A → 4A there are three direct contact points to be formed, whereas for 3A → 4D there are only two. Thus 4D may be more easily formed than 4A due to a reduced electrostatic barrier. We note that the latter factor is not considered at all in a one-component model with a Yukawa potential. Furthermore, we stress that a Yukawa potential should break down at short distances and thus fail in describing aggregation of particles. Now although there is no structural frustration in the 4D → 4A transition, there is only one path, if no bonds are broken; one or both of the two end particles must “roll” around the central two. This 4D → 4A transformation results in a decrease in d, which may be prevented by electrostatic interactions. Thus, once 4D is formed, an electrostatic energy barrier suppresses the transformation from 4D to 4A. The resulting kinetic arrest then leads to a relatively high 4D population. In this way favoured 4D formation and the suppression of 4D → 4A transformation may cause the high fraction of 4D.
On the other hand, one might imagine a charging mechanism which leads to a scenario where the equilibrium populations are a distribution dominated by both 4D and 4A as found. But in equilibrium, the population should respond to increasing the strength of attraction by a factor of three [Fig. 2b], which it does not. This suggests that some form of kinetic arrest is more likely. Our results suggest that it is not so difficult to make a 3A triangle from a linear cluster. Although the reason for the difference is not immediately clear, we note that the linear → 3A transition is not geometrically constrained to follow a single path, unlike the 4D → 4A transition.
Instead, we shall argue that a self-induced anisotropic distribution of charge on the colloids leads to an electrostatic energy barrier which suppresses the 4D → 4A transition. While electrostatic charging mechanisms in these non-aqueous systems are not yet fully understood, we suppose that charging is related to a large number of ionizable groups on the colloid surface, few of which ionize due to the apolar nature of the system. Thus, we may assume that the charge sites, which are capable of dissociating by yielding ions, distribute “homogeneously” on the colloidal surface. To probe the degree of dissociation of ionizable groups, we measured the conductivity of the system as a function of cp with dielectric spectroscopy (Fig. 4). As we do not add salt, we assume the system is in the counter-ion dominated regime. What is evident from Fig. 4 is that the introduction of the colloids massively increases the conductivity relative to the pure solvent suggesting some ion dissociation from the colloid surface. Adding polymer then decreases the conductivity. We associate this reduction in ionic strength (charge per colloid) with clustering. While precise determination of the ionic strength from conductivity measurements requires detailed knowledge of the ionic species present, assuming Walden's rule and a typical limiting molar conductance for ions in these systems of 4 cm2mol−1 29 we arrive at an ionic strength around 10−10 M, consistent with the Debye length κ−1 ~ 2σ found with our Monte Carlo simulations (Fig. 1b).
Figure 4 indicates the reduction of colloid surface charge due to clustering. To gain an understanding of how the charge on two approaching colloids might be influenced during clustering, we introduce an explicit site primitive model (see Methods). Rather than treating the colloids as a single macroion as is usually done38, we consider Z = 60 separate charging sites distributed over the colloid surface in a truncated icosahedral arrangement. Each monovalent site and ion interacts Coulombically with a hard core. In our model the colloids are 10λB in diameter. A typical surface charge reorganization induced by particle clustering is shown in Fig. 5a, where we can clearly see that ions are more condensed on the surfaces in the region between the colloids. To see the effects of this self-induced anisotropy in the surface charge distribution in a more quantitative manner, we fix two colloids such that their surfaces are separated by a distance h [the inset of Fig. 5b]. Ions closer than 1.615λB to a given site are considered to be bound. We plot the degree of anisotropy 〈−cos θ〉 where θ is the angle between uncharged sites and the line connecting the colloid centres as defined in the inset in Fig. 5b as a function of surface separation. For symmetric distributions 〈−cos θ〉 = 0, but decreasing h leads to more condensation since ions between the colloids experience a higher density of charging sites. This in turn causes a reduction of free counterions and anisotropic surface charge distributions develop as a consequence (Fig. 5). While we do not capture the full experimental parameters, we argue that these features are generic to the ion condensation (weak charging) regime. This mechanism is reminiscent of ion condensation in polyelectrolytes39 and may also be relevant to aggregation/crystallisation in proteins35. Stablisation of 4D clusters may be achieved by such an anisotropic charge distribution as follows. Consider the schematic in the inset of Fig. 5b. At contact, if the particles rotate, the back faces of the colloids move closer together. These typically carry more charge, leading to an electrostatic barrier to rotation. The maximum value of such an electrostatic barrier is dependent upon the size of the ion binding sites and whether or not these stay unbound as the colloids rotate. However, given that the Bjerrum length is ~ 25 nm, clearly it is possible for unbound sites to generate significant electrostatic barriers to rotation. For example in the case of 6 sites of nanometre diameter on the Cartesian axes of a 2 μm colloid leads to electrostatic energies induced by rotation of up to 20 kBT (see Supplementary Information).
Self-organization of the surface charge of colloids due to clustering.
(a), Simulation snapshot of the explicit site Primitive Model. Here the separation between the colloid surfaces is set to h = 0.05σ. Sites and ions are shown in red and cyan respectively (actual size). Note enhanced condensation of ions between colloids. (b), Charge anisotropy order parameter 〈−cos θ〉 as a function of surface to surface distance h. Line is a guide to the eye. Inset defines θ and h. Uncharged (bound) sites are shown in blue, charged in red.
While the arguments above indicate that an anisotropic charge distribution can form and stabilise the 4D clusters, normally one expects that small ions reorganise very much faster than colloids rotate and thus any charge distribution would equilibrate on timescales associated with the 4D → 4A transition. Remarkably, in our system this appears not to be the case. Such coupling of timescales between colloids and small ions required occurs when the colloid rotation time is comparable to or shorter than the time associated with the reorganization of ions bound to groups on the colloid surface. The former is the order of τR ~ 8πη(σ/2)3ψ2/kBT, where η is the solvent viscosity and ψ is the angle subtended by the region of surface charge inhomogeneity induced around contact between two colloids. On the other hand, the latter is controlled by escape events of ions from the electrostatic trapping. The characteristic size of the region of surface charge inhomogeneity around contact is of the order of  . Thus
. Thus  so that the characteristic rotational diffusion time τR is of the order of 10−1 s. On the other hand, the escape time of ions from the Coulomb trapping is rather long because of a very high binding energy for ions of size aion, (λB/aion)kBT, which corresponds to ~ 25kBT for aion = 1 nm. Furthermore, ions have to diffuse a distance of order λB to escape from the electrostatic potential of their binding sites. Thus, the time required for surface charge rearrangement may easily exceed 1 s (
so that the characteristic rotational diffusion time τR is of the order of 10−1 s. On the other hand, the escape time of ions from the Coulomb trapping is rather long because of a very high binding energy for ions of size aion, (λB/aion)kBT, which corresponds to ~ 25kBT for aion = 1 nm. Furthermore, ions have to diffuse a distance of order λB to escape from the electrostatic potential of their binding sites. Thus, the time required for surface charge rearrangement may easily exceed 1 s ( ). It is worth noting that this slow surface charge rearrangement is supported by the fact that the time taken for electrostatic equilibration is hours or even days in these systems13,40. We have argued that reorganization of the self-induced surface charge distribution is slow enough that its electrostatic energy barrier can prevent rotation of colloids and affect the selection of cluster configurations. Since the discussion here is rather speculative, however, further careful theoretical and experimental studies are highly desirable on this intriguing problem. Key questions to be addressed include the kinetic stability of the clusters we observe. While we observe no change in the populations of the different clusters as a function of time, our experiments are limited to around 6 hours. On much longer timescales, one expects that the surface charge may unbind and reorganise at the same time as a fluctuation leads to an attempted 4D → 4A transition, thus the 4A (and 5A etc) population should increase given sufficient time.
). It is worth noting that this slow surface charge rearrangement is supported by the fact that the time taken for electrostatic equilibration is hours or even days in these systems13,40. We have argued that reorganization of the self-induced surface charge distribution is slow enough that its electrostatic energy barrier can prevent rotation of colloids and affect the selection of cluster configurations. Since the discussion here is rather speculative, however, further careful theoretical and experimental studies are highly desirable on this intriguing problem. Key questions to be addressed include the kinetic stability of the clusters we observe. While we observe no change in the populations of the different clusters as a function of time, our experiments are limited to around 6 hours. On much longer timescales, one expects that the surface charge may unbind and reorganise at the same time as a fluctuation leads to an attempted 4D → 4A transition, thus the 4A (and 5A etc) population should increase given sufficient time.
We conclude that the one-component description is breaking down in this simple colloidal system on a qualitative level. We emphasize that weak anisotropic charging of just a few elementary charges on large colloids has a profound influence on the kinetic pathway these clusters take. Our results form the beginnings of an understanding of self-assembly of colloidal clusters and molecules as a function of attraction strength; we hope they will stimulate the development of more powerful models based on the explicit site primitive model introduced here. These are needed to realise the potential of self-assembled nanostructures: our results emphasize how challenging it can be even to assemble small clusters of spheres, doubtless more complex geometries will yield further surprises. In the case of m = 6, two structures with similar energies compete, however, here the 6Z polytetrahedron forms instead of the 6A octahedron. Although equilibrium arguments favour this trend, that the population of 6A is zero suggests a stronger driving force. We note that 6Z is structurally similar to 5A and thus may be kinetically favoured. The yield of the fivefold symmetric 7A shows signs of frustration at relatively deep quenches, reminiscent of patchy particles15.
Methods
Experimental
We used poly(methyl methacrylate) (PMMA) colloids sterically stabilized with polyhydroxyl steric acid. The colloids were labelled with fluorescent rhodamine dye and had a diameter of σ = 2.0 μm and a polydispersity of 4% as determined with static light scattering. The van der Waals interactions are neglected by closely matching the refractive index between the solvent and particles, sedimentation is avoided by matching the density. The colloid volume fraction was φ ≈ 0.02. We used a solvent composition of approximately 0.373 cis decalin, 0.093 cyclohexyl bromide and 0.533 tetrachloroethylene by mass, in which the dielectric constant εR ≈ 2.9. This is a good solvent for the polymer, polystyrene (PS). We used a molecular weight of 3.0 × 107, where our measurements of the interactions agreed well with the Asakura-Oosawa (AO) model27 with a polymer-colloid size ratio q ≈ 0.22, which corresponds to a Morse potential with ρ0 = 33.141. We studied the system using confocal microscopy at the single particle level, using a Leica SP5, with which we track the particle coordinates to an accuracy of around 100 nm. We identify clusters based upon the topology of their bonds25 and impose a bond length of 1.4σ (see Supplementary Information for further details). This slightly larger value than the range of the attractive interaction reflects particle tracking errors and polydispersity. Our results are robust to reasonable changes in the bond length. We sampled typically 105 coordinates per state point. No change in the cluster populations was observed on the timescale of the experiments (6 hours). We compare the results with Monte Carlo simulations of the Yukawa model13,27,42, where each cluster is treated as a single particle. This enables an approximate determination of the colloid charge29,43,44.
Explicit site primitive model simulation
Instead of the one-component description which integrates out small ions and leads to a Yukawa interaction between two colloids45, the Primitive Model38,46 treats small ions and colloids (macroions) on an equal footing. The solvent is treated as a dielectric medium and each ion and colloid interact Coulombically.
Here we extend the Primitive Model to treat each charging site on the colloid individually. In the experimental system of interest the total number of sites is very large and well beyond current simulation capabilities. Instead we consider 60 sites, arranged as a truncated icosahedron, the same arrangement as Carbon atoms in C60. This specific arrangement is chosen to realize a homogeneous distribution of charging sites on the particle surface and should not influence the main conclusion.
The lengthscale for electrostatic coupling is the Bjerrum length. In particular, we seek that the site-site interaction is of order of the Bjerrum lengh λB. We therefore selected the following parameters. The colloid diameter σ = 10λB, the sites and ion diameters are σi = λB. Sites and ions have hard cores and are excluded from the colloid interior. The Coulomb interaction is kBT at contact by construction. Within a fairly wide parameter space (a factor of 3 change in ion-site coupling and a factor of 2 change in λB), the results obtained for 60 sites per colloid do not qualitatively differ. By comparison, the experimental system has σ = 2.0 μm and λB ≈ 25 nm, but the number of sites is  .
.
Periodic boundary conditions are used and the colloid volume fraction was set to φ = 0.001. We implemented an Ewald sum47 but found that it had no measurable effect on our results. The separation of two (fixed) colloids is varied between simulations. A typical snapshot is shown in Fig. 5a for a colloid surface separation h = 0.05σ.
We introduce 〈−cos θ〉 as an order parameter to describe the degree of asymmetry in the charge distribution where the angle brackets denote a statistical average. θ is the angle between a line connecting an unbound site and the center of the colloid on which is it situated and the line between the colloid centers [see Fig. 5a].
We implement two types of Monte Carlo (MC) move. Standard displacements and binding/unbinding moves. Binding/unbinding moves are as follows. Either a bound ion is selected at random and moved to an allowed part of the simulation box where it is not bound, or an unbound ion is moved to a position where it was bound to a previously unbound site. Binding and unbinding moves are attempted with equal probability and accepted according to standard Metropolis MC42. Standard displacements or binding/unbinding are attempted with equal probability. This satisfies detailed balance and accelerates equilibration by several orders of magnitude. We found after attempting to move every ion 300 times, that no change in potential energy energy was observed and we assumed the system was equilibrated. Prior to production runs we updated an initially randomized system 300 times with 2Z = 120 attempted moves each. We found that longer equilibrations up to 1 × 105 MC sweeps led to no measurable change in the results.
References
Calvo, F., Doye, J. P. K. & Wales, D. J. Energy landscapes of colloidal clusters: Thermodynamics and rearrangement mechanisms. Nanoscale 4, 1085–1100 (2012).
Meng, G., Arkus, N., Brenner, M. P. & Manoharan, V. N. The free-energy landscape of clusters of attractive hard spheres. Science 327, 560–563 (2010).
Chen, Q. et al. Supracolloidal reaction kinetics of janus spheres. Science 331, 199–202 (2011).
Yunker, P. J., Chen, K., Zhang, Z. & Yodh, A. G. Phonon spectra, nearest neighbors and mechanical stability of disordered colloidal clusters with attractive interactions. Phys. Rev. Lett. 106, 225503 (2011).
Chen, Q., Bae, S. C. & Granick, S. Staged self-assembly of colloidal metastructures. J. Am. Chem. Soc. 134, 11080–11083 (2012).
Nie, Z., Petukhova, A. & Kumacheva, E. Properties and emerging applications of self-assembled structures made from inorganic nanoparticles. Nature Nanotech. 5, 15–25 (2009).
Manoharan, V. N., Elesser, M. T. & Pine, D. J. Dense packing and symmetry in small clusters of microspheres. Science 301, 483–487 (2003).
Kraft, D. J., Groenewold, J. & Kegel, W. K. Colloidal molecules with well-controlled bond angles. Soft Matter 5, 3823–3826 (2009).
Wang, Y. et al. Colloids with valence and specific directional bonding. Nature 491, 51–56 (2012).
Segre, P. N., Prasad, V., Schofield, A. B. & Weitz, D. A. Glasslike kinetic arrest at the colloidal-gelation transition. Phys. Rev. Lett. 86, 6042–6045 (2001).
Stradner, A. et al. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 432, 492–495 (2004).
Campbell, A. I., Anderson, V. J., van Duijneveldt, J. S. & Bartlett, P. Dynamical arrest in attractive colloids: The effect of long-range repulsion. Phys. Rev. Lett. 94, 208301 (2005).
Klix, C. L., Royall, C. P. & Tanaka, H. Structural and dynamical features of multiple metastable glassy states in a colloidal system with competing interactions. Phys. Rev. Lett. 104, 165702 (2010).
Zerrouki, D., Baudry, J., Pine, D., Chaikin, P. & Bibette, J. Chrial colloidal clusters. Nature 455, 380–382 (2008).
Wilber, A. W. et al. Reversible self-assembly of patchy particles into monodisperse clusters. J. Chem. Phys. 127, 085106 (2007).
Dijkstra, M., van Roij, R. & Evans, R. Phase behaviour and structure of model colloid-polymer mixtures. J. Phys.: Condens. Matter 11, 10079–10106 (1999).
Likos, C. Effective interactions in soft condensed matter physics. Phys. Rep 348, 267–439 (2001).
Hansen, J. P. & Löwen, H. Effective interactions between electric double layers. Annu. Rev. Phys. Chem. 51, 209–242 (2000).
Naji, A., Kanduč, M., Netz, R. R. & Podgornik, R. Exotic electrostatics: Unusual features of electrostatic interactions between macroions in Understanding Soft Condensed Matter via Modeling and Computation. Soft Condensed Matter (World Scientific, Singapore, 2010). Series Editors: Andelman D. and Reiter G., eds.
Kanduč, M., Naji, A., Jho, Y. S., Pincus, P. A. & Podgornik, R. The role of multipoles in counterion-mediated interactions between charged surfaces: strong and weak coupling. J. Phys.: Condens. Matter 21, 424103 (2009).
Jho, Y. S., Safran, S. A., In, M. & Pincus, P. A. Effect of charge inhomogeneity and mobility on colloid aggregation. Langmuir 28, 8329–8336 (2012).
Doye, J. P. K., Wales, D. J. & Berry, R. S. The effect of the range of the potential on the structures of clusters. J. Chem. Phys. 103, 4234–4249 (1995).
Mossa, S., Sciortino, F., Tartaglia, P. & Zaccarelli, E. Ground-state clusters for short-range attractive and long-range repulsive potentials. Langmuir 20, 10756–10763 (2004).
Malins, A., Williams, S. R., Eggers, J., Tanaka, H. & Royall, C. P. Geometric frustration in small colloidal clusters. J. Phys.: Condens. Matter 21, 425103 (2009).
Williams, S. R. Topological clasification of clusters in condensed phases. (http://arxiv.org/abs/0705.0203) arXiv:0705.0203v1 [cond-mat.soft] (2007).
Royall, C. P., Williams, S. R., Ohtsuka, T. & Tanaka, H. Direct observation of a local structural mechanism for dynamic arrest. Nature Mater. 7, 556–561 (2008).
Royall, C. P., Louis, A. A. & Tanaka, H. Measuring colloidal interactions with confocal microscopy. J. Chem. Phys. 127, 044507 (2007).
Sciortino, F., Mossa, S., Zaccarelli, E. & Tartaglia, P. Equilibrium cluster phases and low-density arrested disordered states: The role of short-range attraction and long-range repulsion. Phys. Rev. Lett. 93, 055701 (2004).
Royall, C. P., Leunissen, M. E., Hynninen, A. P., Dijkstra, M. & van Blaaderen, A. Re-entrant melting and freezing in a model system of charged colloids. J. Chem. Phys. 124, 244706 (2006).
Roberts, G. S., Wood, T. A., Frith, W. J. & Bartlett, P. Direct measurement of the effective charge in nonpolar suspensions by optical tracking of single particles. J. Chem. Phys. 126, 194503 (2007).
Malins, A., Williams, S. R., Eggers, J., Tanaka, H. & Royall, C. P. The effect of inter-cluster interactions on the structure of colloidal clusters. J. Non-Cryst. Solids 357, 760–766 (2011).
Doye, J. P. K., Wales, D. J. & Simdyankin, S. I. Global optimization and the energy landscapes of dzugutov clusters. Faraday Discuss. 118, 159–170 (2001).
Groenewold, J. & Kegel, W. K. Anomalously large equilibrium clusters of colloids. J. Phys. Chem. B. 105, 11702–11709 (2001).
Louis, A. A., Bolhuis, P. G., Meijer, E. J. & Hansen, J. P. Polymer induced depletion potentials in polymer-colloid mixtures. J. Chem. Phys. 117, 1893–1907 (2002).
Schmit, J. D., Whitelam, S. & Dill, K. Electrostatics and aggregation: How charge can turn a crystal into a gel. J. Chem. Phys. 135, 085103 (2011).
Hong, L., Cacciuto, A., Luijten, E. & Granick, S. Clusters of charged janus spheres. NanoLett. 6, 2510–2514 (2006).
Hoffmann, N., Likos, C. N. & Hansen, J. P. Linear screening of the electrostatic potential around spherical particles with non-spherical charge patterns. Mol. Phys. 102, 857–867 (2004).
Linse, P. Advanced computer simulation approaches formation soft matter sciences ii. Adv. Polym. Sci. 185, 111–162 (2005).
Levin, Y. Electrostatic correlations: from plasma to biology. Rep. Prog. Phys. 65, 1577–1632 (2002).
Royall, C. P., Leunissen, M. E. & van Blaaderen, A. A new colloidal model system to study long-range interactions quantitatively in real space. J. Phys.: Condens. Matter 15, S3581–S3596 (2003).
Noro, M. G. & Frenkel, D. Extended corresponding-states behavior for particles with variable range attractions. J. Chem. Phys. 113, 2941–2944 (2000).
Frenkel, D. & Smit, B. Understanding Molecular Simulation: from Algorithms to Applications (New York: Academic, 2001).
Royall, C. P., Aarts, D. G. A. L. & Tanaka, H. Fluid structure in colloid-polymer mixtures: the competition between electrostatics and depletion. J. Phys: Condens. Matter 17, S3401–S3408 (2005).
Royall, C. P., Poon, W. C. K. & Weeks, E. R. In search of colloidal hard spheres. Soft Matter 9, 17–27 (2013).
Verwey, E. J. W. & Overbeek, J. Theory of the Stability of Lyophobic Colloids (Elsevier, Amsterdam, 1948).
Hynninen, A. P. & Dijkstra, M. Melting line of charged colloids from primitive model simulations. J. Chem. Phys. 123, 244902 (2005).
Allen, M. P. & Tildesley, D. J. Computer Simulation of Liquids (Oxford University Press, 1987).
Acknowledgements
The authors are grateful to Wuge Briscoe, Didi Derks, Jeroen van Duijneveldt, Rob Jack and Matthias Schmidt for a critical reading of the manuscript. CLK thanks the Deutscher Akademischer Austauschdienst for financial assistance. HT acknowledges Grant-in-Aid for Scientific Research (S) and Specially Promoted Research from JSPS and the Aihara Project, the FIRST program from JSPS, initiated by CSTP. CPR acknowledges the Royal Society for financial support.
Author information
Authors and Affiliations
Contributions
H.T. and C.P.R. conceived the project, C.L.K. performed colloidal experiments, K.M. performed electrical measurements, S.R.W. and C.P.R. analysed the data, A.M. and C.P.R. performed simulations and H.T. and C.P.R. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Klix, C., Murata, Ki., Tanaka, H. et al. Novel kinetic trapping in charged colloidal clusters due to self-induced surface charge organization. Sci Rep 3, 2072 (2013). https://doi.org/10.1038/srep02072
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02072
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.