Introduction

Quantum capacitance and compressibility are critical quantities reflecting the fundamental physics of electron-electron (e-e) interactions1,2,3. The compressibility of two-dimensional electron gas systems can have a negative sign when the influence of e-e interactions on the density of states (DOS) is drastic, in particular in the samples having very low electron density n and being subjected to a high magnetic field B4,5. But single-layer graphene (SLG), a truly two-dimensional structure with a honeycomb lattice and a linear energy spectrum near the intersection of the electron and hole cones in its band structure6,7,8,9, exhibits very weak e-e interaction behavior. The single-electron model is usually sufficient to describe the electron behavior in SLG. The weak e-e interactions in SLG are mainly due to the exchange and correlation energies’ cancelling each other out10,11, resulting in a positive exchange self-energy according to renormalization group theory12,13,14. Therefore, the inverse quantum capacitance (or inverse compressibility) is only modified by a small positive logarithmic correction in comparison with the one that ignores the e-e interactions12. Recently, G. L. Yu et al. reported that in high-quality pristine graphene samples, negative quantum capacitance phenomenon can be observed at half filling factors due to many-body effects under strong magnetic fields15. However, the negative quantum capacitance phenomenon in disordered graphene remains unexplored.

Unlike the experiment carried out by G.L. Yu et al. in which the kinetic energy is suppressed due to the formation of Landau levels, in this work, we show the first experimental evidence of reaching the strongly correlated electron regime induced by nearly dispersionless impurity bands in graphene, in the absence of a magnetic field. SLG decorated with a high density of Ag adatoms shows the unconventional phenomenon of negative quantum capacitance even in the absence of a magnetic field. This phenomenon is enhanced as the strength of the magnetic field increases. We believe that the midgap states induced by a high density of Ag adatoms deposited on SLG are responsible for this interesting experimental observation. The varied energy dispersion relationship as well as the emergence of nearly dispersionless impurity bands near the zero Fermi energy16,17,18 leads to the suppression of the kinetic energy of electrons and the significant changes of Coulomb interactions in Ag-adsorbed SLG, particularly in the presence of a magnetic field. The capacitance measurements at different temperatures and under different strength of a magnetic field clearly demonstrate that the Coulomb interaction and Landau level (LL) quantization have a strong influence over the negative quantum capacitance phenomenon.

Results

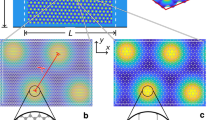
Figure 1(a) schematically shows the SiO2/Ag-adsorbed graphene/Y2O3 sandwiched capacitor and an optical image of one of our devices is revealed in Figure 1(b). The total capacitance Ctg consisting of the oxide layer capacitance Cox and graphene quantum capacitance Cq in a serial configuration is shown in Figure 1(c) (see details in Methods). Our tight-binding calculations for SLG decorated with a high density of Ag adatoms (the impurity concentration ni = 1 %) show several resonant impurity bands as well as a dispersionless band near the Fermi energy EF = 0 (see Figure 1(d))19. Obviously, these changes in the quasi-particle band structure of Ag-adsorbed graphene lead to a different low-energy excitation spectrum and thus produce midgap states (instead of the vanishing DOS in pristine SLG) in the vicinity of the charge neutrality point (CNP)16,17,19,20,21,22. Quantum capacitance (directly proportional to graphene DOS) measurements provide an effective method to probe the midgap states in graphene. As shown in Figure 2(a), a robust peak was detected when measuring the total capacitance Ctg versus the applied top gate voltage of our Ag-adsorbed SLG samples at T = 2 K, confirming that Ag adatoms act as resonant impurities and create obvious midgap states near the CNP18,21,23,24,25.

Figure 1
figure 1

(a) Schematic diagram of the Ag-adsorbed single-layer graphene capacitor.(b) An optical image of the Ag-adsorbed single-layer graphene capacitor device; dashed line represents the graphene flake and the scale bar is 5 μm. (c) Circuit diagram of the capacitance measurements of Y2O3 top-gated graphene devices. (d) Density plot of spectral function A (E,k) in k − E plane for impurity concentration ni = 1%, where a = 0.142 nm is the nearest-neighbor distance.

Full size image
Figure 2
figure 2

(a) Curve of the total capacitance Ctg versus top gate voltage Vtg of the Ag-adsorbed single-layer graphene capacitor measured at T = 2 K where the gray dashed line denotes the value of Cox = 0.65 μF/cm2.(b) The relationship between chemical potential μ versus top gate Vtg obtained from the data shown in Figure 2(a), where the red arrow denotes the abnormal decline of κ−1 versus Vtg. (c) Inverse compressibility κ−1 of Ag-adsorbed graphene measured at T = 2 K where the orange dashed line denotes the zero value of κ−1.

Full size image

The quantum capacitance Cq of graphene can be calculated from Cq−1 = Ctg−1 − Cox−1 26,27,28,29. The oxide layer capacitance Cox was obtained by measuring the internal reference parallel-plate capacitors (Au/Y2O3/Au), of which the Y2O3 layers were prepared under the same experimental conditions as those for the SLG quantum capacitors27,28,29. Surprisingly, the values of Ctg in the energy region near the CNP where the robust midgap state peak appears always exceed that of the oxide layer capacitance Cox, a very clear sign of negative quantum capacitance Cq15. In Figure 2 (a), the dashed line denotes the value of Cox = 0.65 μF/cm2 measured at temperature T = 2 K and thus Cq is negative in the region above the dashed line. The midgap states induced by Ag adatoms obviously play a critical role in the formation of the negative quantum capacitance.

The variation in the chemical potential μ (equivalent to the Fermi energy EF) as a function of top gate voltage Vtg can be calculated from the integral form of the charge conservation relation 27,30,31, where e is the elementary charge and the capacitance data are measured at T = 2 K. The result is shown in Figure 2 (b). Unlike in pristine SLG, an abnormal decline in the curve of μ versus Vtg occurs in the Ag-adsorbed SLG near μ = 0. The fact that the total energy decreases when more electrons are introduced to the sample by increasing the top gate voltage Vtg, implies that the energy of the incoming electrons in the region of midgap states is negative.

Discussion

The chemical potential μ of the electrons in SLG consists of the kinetic energy of Ek and the Coulomb interaction energy among electrons Ec and can be denoted by 1,3,11,13. As the tight-binding results shown in Figure 1 (d), in low carrier density regions, the electron states would be first filled within the nearly dispersionless bands and thus the kinetic energy Ek is quenched. In this case, the Coulomb interaction energy Ec becomes dominant. The Coulomb interaction energy Ec can also vary dramatically as a consequence of the formation of midgap states. The inverse compressibility κ−1, defined as the derivative of chemical potential μ with respect to carrier density n, , is also determined by the kinetic energy Ek and the Coulomb energy Ec1,12,13. The experimental values of κ−1 can be obtained by , as shown in Figure 2 (c). In previous theoretical studies, it has been suggested that midgap states enhance the Coulomb interactions and the correction term induced by midgap states has a negative sign, leading to the reduction of κ~1. The expression of κ−1 affected by midgap states is represented as1,32,33,34

where c is a positive numerical constant, Δ is a positive dimensionless number characterizing the strength of midgap states and is a high momentum cutoff of the order of the inverse of the lattice constant. Note that the second term in the bracket arising from the midgap states correction is negative and becomes significant if wave vector k is very small. Thus the experimental observation of negative compressibility or negative quantum capacitance in Ag-adsorbed SLG can be naturally understood by the fact that the midgap states lead to a negative correction of κ−1.

The magneto-capacitance measurements for the Ag-adsorbed SLG further support a correlation between the midgap states and graphene negative quantum capacitance, particularly in the presence of LL quantization. As shown in Figure 3, Ctg oscillates (against top gate voltage Vtg) due to LL quantization under a strong magnetic field of B = 8 T at T = 2 K35. Because of the thermal-activated fluctuation of carrier density n, the LLs broaden when temperature increases29,35,36. At 200 K, LLs at N = 0, ±1 are still recognizable, while the other LLs are smeared. At B = 8 T and T = 2 K, the quantum capacitances measured at LL positions of N = ±1 and N = −2 where the midgap states have less overlap with the LLs also become negative. The signatures of negative capacitance at these LL locations disappear gradually as temperature increases to 200 K. The temperature dependence of the negative quantum capacitance Cq at LL positions of N = ±1 and N = −2 obviously reflects the high correlation of the degree of LL quantization with the negative Cq phenomenon. This phenomenon can be explained qualitatively by the fact that a strong magnetic field can effectively quench the kinetic energy Ek of electrons due to LL quantization and thus the negative Coulomb energy dominates and leads to the negative Cq15,37.

Figure 3
figure 3

Magneto-capacitance Ctg measured at B = 8 T versus top gate voltage Vtg of the Ag-adsorbed single-layer graphene capacitor obtained at (a) T = 2 K (blue line), (b) T = 100 K (red line) and (c) T = 200 K (green line); the results measured at B = 0 T (dashed lines) are shown here for comparison.

Full size image

Near the CNP, the midgap states and the LL at N = 0 overlap forming the “central peak” of the negative Cq. The intensity of this central peak is not sensitive to temperature, unlike the behavior of other LLs as shown in Figures 3 (a)–(c). These experimental results indicate that the Ek of electrons near the CNP in Ag-adsorbed SLG has been effectively suppressed due to the formation of the dispersionless impurity band at EF = 0. In this case, the magnetic quenching effect on the Ek attributed to the N = 0 LL is insignificant and we can observe very obvious negative Cq phenomenon near CNP even in the absence of magnetic field. However, we do observe that the negative Cq is very sensitive to the variation in a magnetic field (see Figure 4 (a)). Since the complete quenching effect on Ek near EF = 0 occurs with or without a magnetic field (based on the above analysis), we ascribe the magnetic-field-enhanced negative Cq effect near the CNP to the contribution of the Coulomb interaction energy Ec, which has been greatly altered due to the presence of a magnetic field in our samples. Under a magnetic field, electronic motion in SLG is localized and a huge population induced by the formation of zero LL leads to a massive degeneracy near CNP7. Thus the Coulomb interaction energy should increase and the negative Cq will be enhanced, as the magnetic field becomes stronger.

Figure 4
figure 4

(a) Total capacitance Ctg versus top gate voltage Vtg of the Ag-adsorbed single-layer graphene capacitor measured near the CNP at B = 0 T (red line), B = 5 T (green line), B = 7 T (blue line) and B = 8 T (orange line).The gray dashed line denotes the value of Cox = 0.65 μF/cm2. (b) Two-dimensional mapping of Ctg measured at T = 2 K as a function of top gate voltage Vtg and magnetic field B, where the regions in which the negative quantum capacitance (i.e. Ctg > Cox = 0.65 μF/cm2) emerges are colored in yellow and the numbers above the figure denote the LL positions.

Full size image

The variation in Ctg as a function of B and Vtg measured at T = 2 K is revealed in Figure 4 (b). The general features of the LLs (particularly the high energy LLs) for the Ag-adsorbed SLG follow the prediction of LL quantization theory for pristine SLG. The regions colored in yellow indicate the negative Cq regions, which start to emerge at the N = ±1 LLs as B increases to 2 ~ 3 T. This is very different from the weak negative Cq observed in high-quality pristine SLG under a strong magnetic field B = 5 ~ 25 T15. We believe that weak resonant impurity bands exist at some distance away from EF = 0. The midgap states induced by resonant impurities should also influence the electrons located at some distance away from the CNP (e.g., at the N = ±1 LLs), although their effects on negative Cq are not as strong as those of the midgap states that are close to the CNP. Therefore, the negative Cq in the presence of a magnetic field in Ag-adsorbed SLG should mainly incorporate the effects from the suppression of Ek and the enhancement of Ec, both of which are directly correlated with magnetic fields and various resonant impurity bands.

In summary, we find that the novel phenomenon of negative quantum capacitance observed in single-layer graphene decorated with a high density of Ag adatoms is attributed to the midgap states induced by the resonant impurities of the Ag adatoms. Owing to these Ag-induced midgap states, the kinetic energy of the electrons near the zero Fermi energy is effectively quenched and the Coulomb interaction energy is varied dramatically and the combination of these two events leads to the abnormal negative quantum capacitance of the “central peak” in the absence of a magnetic field. In the presence of a magnetic field, the negative quantum capacitance is dramatically enhanced. The emergence of the negative quantum capacitance away from the CNP is intimately associated with the degree of Landau level quantization, while the magnetic-field-enhanced Coulomb interactions give rise to the increase of negative quantum capacitance near the CNP with the magnetic fields.

Methods

Single-layer graphene (SLG) samples were prepared by the micromechanical exfoliation of Kish graphite and placed on silicon substrates with 300 nm-thick SiO2. Raman spectroscopy has been used to identify these samples are single-layer graphene. Ag adatoms were introduced to SLG by DC plasma sputtering in high base vacuum conditions (10−7 torr) at room temperature38,39. An ultrathin yttrium layer (5 nm in thickness) was deposited on the Ag-adsorbed SLG by e-beam evaporation and then the SLG was oxidized in air at 180°C for 30 minutes27,29. The fabrication of drain/source and top gate electrodes (Ti/Au = 5/40 nm) was performed by conventional electron-beam lithography techniques (Raith e-Line Nanoengineering Workstation and AST electron-beam evaporation system)38,39. As shown in Figure 1, the total capacitance Ctg, in a series of the oxide layer capacitance Cox and graphene quantum capacitance Cq, was measured by an integrated capacitance bridge for high sensitivity. This capacitance bridge delivered extremely high resolution of atto farad (aF) under very small excitation (~0.1 mV) driving any possible parasitic capacitance by a high mobility electron transistor (HMET)26,27,35,38,40,41.