Abstract
By means of density functional theory computations, we demonstrated that C2H4 is the ideal terminal group for zigzag graphene nanoribbons (zGNRs) in terms of preserving the edge magnetism with experimental feasibility. The C2H4 terminated zGNRs (C2H4-zGNRs) with pure sp2 coordinated edges can be stabilized at rather mild experimental conditions and meanwhile reproduce the electronic and magnetic properties of those hydrogen terminated zGNRs. Interestingly, the electronic structures and relative stability of C2H4-zGNRs with different edge configurations can be well interpreted by employing the Clar's rule. The multiple edge hyperconjugation interactions are responsible for the enhanced stability of the sp2 coordinated edges of C2H4-zGNRs. Moreover, we demonstrated that even pure sp2 termination is not a guarantee for edge magnetism, for example, C2H2 termination can couple to the π-electron system of zGNRs and destroy the magnetism. Our studies would pave the way for the application of zGNRs in spintronics.
Similar content being viewed by others
Introduction
Since its experimental realization in 20041,2, graphene, the first strict two-dimensional (2D) crystal with one-atomic thickness, has been a subject of great interest due to its excellent properties and promising applications3,4,5. Interestingly, one dimensional (1D) graphene nanoribbons (GNRs) can also be yielded by cutting graphene in the nano-scaled width. Depending on the cutting direction, two unique types of edges can be obtained: zigzag and armchair. Different from graphene which is actually semimetal, both zigzag and armchair GNRs have a nonzero band gap, which has been confirmed both theoretically6,7 and experimentally8,9. Moreover, the edge geometry also makes a huge difference in the π-electron structure at the edges. As early as in 1996, Fujita et al.10 revealed that zigzag GNRs (zGNRs) have peculiar localized edge states (completely absent in the armchair edge), which give rise to the quite flat bands near the Fermi level11. By employing the Hubbard model with the unrestricted Hartree-Fock approximation, Fujita et al.10,12 also deduced that the edge states of zGNRs are ferromagnetically (FM) coupled on each edge but antiferromagnetically (AFM) coupled between two edges. In 2006, Son et al.13 found that the edge states of zGNRs in different spin channels response oppositely to the transverse external electric field and thus zGNRs can be half-metallic (metallic for one spin channel and insulating for the other) under a critical value of electric field. Later theoretical studies demonstrated that selective edge modification14,15 can also tune zGNRs into half-metallic. Therefore, zGNRs have very promising applications in future spintronics.
However, there is a large gap between theoretical prediction and experimental realization. The edge states of zGNRs are very reactive16 and thus cause instability, whereas armchair edges are more stable17,18,19. As a consequence, most synthesized nanographenes have armchair peripheries20,21 and the synthesis of GNRs with consecutive zigzag edges has been rather difficult for a long time. Encouragingly, experimental peers have achieved great progress recently in fabricating GNRs with smooth zigzag edges22,23,24,25,26 and the localized edge states have been vigorously confirmed by scanning tunneling microscopy (STM) and spectroscopy27,28,29,30,31. However, the edge magnetism of zGNRs has been scarcely detected experimentally32,33, because, to preserve the edge magnetism, the edge sites of zGNRs should have the pure sp2 coordination. Unfortunately, density functional theory (DFT) computations by Wassmann et al.34 demonstrated that the pure sp2 coordinated edges of hydrogen terminated zGNRs (H-zGNRs) can be stabilized only at extremely low hydrogen concentration, which is rather challenging experimentally. Under normal conditions, the edge sites tend to be fully saturated by hydrogen, which directly suppresses the edge magnetism. More seriously, zGNRs are also characterized by the nonmagnetic nature in presence of some typical atmospheric molecules, such as O2, H2O, NH3 and CO235.
Therefore, to preserve the edge magnetism of zGNRs, the first urgent thing is to find a suitable termination group for zGNRs. Recently, Chai et al.36 have suggested that large bulky ligands (i.e. tertiary-butyl, C4H9) terminated zGNRs favor the pure sp2 termination across a broader range of thermodynamic conditions due to the strong steric effect of ligands. Though not mentioned explicitly, the hyperconjugation between the large bulky ligands and the edge states (can be seen as radicals)16,37 also contributes to the enhanced stability of the edge. Then, an interesting question arises: can we use some more simple terminal groups to stabilize sp2 coordinated edges of zGNRs by taking advantage of hyperconjugation interaction?
In this work, by means of systematic DFT computations, we explored the possibility of using ethylene (C2H4), a very simple and common organic molecule, as the terminal group for zGNRs to preserve the edge magnetism. C2H4 was chosen due to two reasons: (1) experimentally C2H4 is an important carbon resource for graphene growth38,39 and thus technically it would be rather practical to use C2H4 as terminal group for zGNRs; (2) after bonding to edges sites, the C–H bonds of C2H4 can have hyperconjugation interaction with edge states. Our computations demonstrated that due to the multiple edge hyperconjugation interactions, sp2 coordinated edges of C2H4 terminated zGNRs (C2H4-zGNRs) can be realized at rather mild experimental conditions and C2H4-zGNRs can well reproduce the electronic and magnetic properties of H-zGNRs.
Results
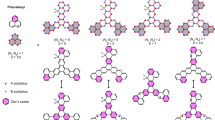
To ascertain whether the edge magnetism of zGRNs can be preserved by C2H4 termination, we need to determine the most stable edge configuration for C2H4-zGNRs firstly. In our computations, C2H4-zGNR with a width parameter of 8 (8-C2H4-zGNR) was chosen as a representative (Figure 1). For simplicity, two edges of 8-C2H4-zGNR were set to have the same configuration. Following the previous convention34,35,36, the edge configurations are denoted with  , where ni = 1, 2 stands for the number of C2H4 molecules bonded to the ith edge site and x is the number of edge sites in a unit cell. Six edge configurations, including z11, z121, z11121, z22, z1122 and z111122 were considered. Here note that different from H, one C2H4 can bond to two edge sites, thus some edge configurations consisting of odd number of sp2 edge sites, such as z12 and z1112, are only available for H termination but not available for C2H4 termination. Moreover, we also considered the reconstructed zigzag edge, in which two hexagons transform into a pentagon and a heptagon, denoted as z(57)19. This haeckelite edge structure has been observed experimentally40. For z(57), two possible edge configurations, including z(57)11 and z(57)22, were investigated.
, where ni = 1, 2 stands for the number of C2H4 molecules bonded to the ith edge site and x is the number of edge sites in a unit cell. Six edge configurations, including z11, z121, z11121, z22, z1122 and z111122 were considered. Here note that different from H, one C2H4 can bond to two edge sites, thus some edge configurations consisting of odd number of sp2 edge sites, such as z12 and z1112, are only available for H termination but not available for C2H4 termination. Moreover, we also considered the reconstructed zigzag edge, in which two hexagons transform into a pentagon and a heptagon, denoted as z(57)19. This haeckelite edge structure has been observed experimentally40. For z(57), two possible edge configurations, including z(57)11 and z(57)22, were investigated.
To compare the stability of these edge configurations, we first computed the edge formation energy ( ) for each configuration, which is defined as:
) for each configuration, which is defined as:

where  ,
,  and
and  are the total energies of the nanoribbon, one carbon atom of graphene and one C2H4 molecule, respectively.
are the total energies of the nanoribbon, one carbon atom of graphene and one C2H4 molecule, respectively.  and
and  are the numbers of carbon atoms and C2H4 groups in the supercell, respectively. L is the length of one unit cell. According to this definition, the edge configurations with lower
are the numbers of carbon atoms and C2H4 groups in the supercell, respectively. L is the length of one unit cell. According to this definition, the edge configurations with lower  values are more favorable energetically at 0 K. For comparison, the
values are more favorable energetically at 0 K. For comparison, the  of 8-H-zGNR with pure sp2 termination (z(H)1) was also computed. The computed
of 8-H-zGNR with pure sp2 termination (z(H)1) was also computed. The computed  of all the considered edge configurations and their corresponding ground states are summarized in Table 1. According to our computations, for C2H4-zGNRs, the nonmagnetic edge configuration z111122 has the lowest value of
of all the considered edge configurations and their corresponding ground states are summarized in Table 1. According to our computations, for C2H4-zGNRs, the nonmagnetic edge configuration z111122 has the lowest value of  , tightly followed by the pure sp2 coordinated edge configuration z11. Especially, the
, tightly followed by the pure sp2 coordinated edge configuration z11. Especially, the  of z11 is lower than z(H)1, implying that C2H4 termination could produce more stable sp2 coordinated edge than hydrogen termination.
of z11 is lower than z(H)1, implying that C2H4 termination could produce more stable sp2 coordinated edge than hydrogen termination.
 ) for all the considered edge configurations of C2H4-terminated 8-zGNRs and their corresponding ground states (GS). The corresponding values for the z1 configuration of H-terminated 8-zGNRs are given for comparison
) for all the considered edge configurations of C2H4-terminated 8-zGNRs and their corresponding ground states (GS). The corresponding values for the z1 configuration of H-terminated 8-zGNRs are given for comparisonHowever, the content of C2H4 changes under real experimental conditions and the chemical potential of C2H4 should be taken into account. Thus, we evaluated the relative stability of different edge configurations for 8-C2H4-zGNR under real experimental conditions by comparing their respective Gibbs formation energy ( ), which is defined as:
), which is defined as:

where  is a function of the temperature T and the partial C2H4 gas pressure P and can be expressed as:
is a function of the temperature T and the partial C2H4 gas pressure P and can be expressed as:

 and
and  are the enthalpy and entropy at the pressure
are the enthalpy and entropy at the pressure  = 1 bar, respectively, the values of which at T = 298 K are obtained from the textbook41. Then, we plotted the curve of
= 1 bar, respectively, the values of which at T = 298 K are obtained from the textbook41. Then, we plotted the curve of  for 8-C2H4-zGNR with different edge configurations as a function of
for 8-C2H4-zGNR with different edge configurations as a function of  in Figure 2. According to the above definition, the most stable edge configuration should have the lowest value of
in Figure 2. According to the above definition, the most stable edge configuration should have the lowest value of  within a given value of
within a given value of  .
.
Gibbs formation energy ( ) as a function of chemical potential (
) as a function of chemical potential ( ) for different edge configurations of 8-C2H4-zGNR.
) for different edge configurations of 8-C2H4-zGNR.
The solid lines denote the stable edge configurations under certain  values. Vertical dashed lines divide the stability regions. The upper axis shows the pressure of C2H4, corresponding to the chemical potential at 298 K. The red dot denotes the position of saturated vapor pressure of C2H4 at 298 K.
values. Vertical dashed lines divide the stability regions. The upper axis shows the pressure of C2H4, corresponding to the chemical potential at 298 K. The red dot denotes the position of saturated vapor pressure of C2H4 at 298 K.
Several conclusions can be drawn from Figure 2. First, the  of z121, z11121, z(57)11, or z(57)22 could never be the lowest at any given value of
of z121, z11121, z(57)11, or z(57)22 could never be the lowest at any given value of  , indicating that these four edge configurations have no chance to be realized under real experimental conditions. Especially, the unfavorability of z(57)11 and z(57)22 suggests that the reconstruction of zigzag edge can be suppressed under the C2H4 environment. Second, the
, indicating that these four edge configurations have no chance to be realized under real experimental conditions. Especially, the unfavorability of z(57)11 and z(57)22 suggests that the reconstruction of zigzag edge can be suppressed under the C2H4 environment. Second, the  of z22 is the lowest when
of z22 is the lowest when  is larger than 2.03 eV, indicating that z22 can be stabilized only at extremely high C2H4 concentration. When
is larger than 2.03 eV, indicating that z22 can be stabilized only at extremely high C2H4 concentration. When  is in the range of [0.44, 2.03] eV, z1122 becomes stable. z111122, which has the lowest value of
is in the range of [0.44, 2.03] eV, z1122 becomes stable. z111122, which has the lowest value of  , is stable only in a rather narrow range of [−0.11, 0.44]. When
, is stable only in a rather narrow range of [−0.11, 0.44]. When  < −0.11 eV, z11 becomes the most stable edge configuration. At room temperature, −0.11 eV of
< −0.11 eV, z11 becomes the most stable edge configuration. At room temperature, −0.11 eV of  corresponds to a C2H4 pressure (P) of 2.45 bar. In other words, if the C2H4 pressure can be controlled to be lower than 2.45 bar at room temperature, which is experimentally rather feasible, the pure sp2 coordinated edges can be stabilized. In sharp contrast, pure sp2 coordinated edges of H-zGNRs can be stabilized only at extremely low hydrogen concentration and thus unlikely to be realized. Therefore, C2H4 is superior to hydrogen as a terminal group for zGNRs in terms of generating pure sp2 coordinated edges and preserving the edge magnetism. Experimentally, C2H4-zGNRs can be synthesized via lithographic patterning of graphene under the C2H4 atmosphere, or by etching the edges of pre-obtained zGNRs using C2H4 gas.
corresponds to a C2H4 pressure (P) of 2.45 bar. In other words, if the C2H4 pressure can be controlled to be lower than 2.45 bar at room temperature, which is experimentally rather feasible, the pure sp2 coordinated edges can be stabilized. In sharp contrast, pure sp2 coordinated edges of H-zGNRs can be stabilized only at extremely low hydrogen concentration and thus unlikely to be realized. Therefore, C2H4 is superior to hydrogen as a terminal group for zGNRs in terms of generating pure sp2 coordinated edges and preserving the edge magnetism. Experimentally, C2H4-zGNRs can be synthesized via lithographic patterning of graphene under the C2H4 atmosphere, or by etching the edges of pre-obtained zGNRs using C2H4 gas.
After establishing that pure sp2 coordinated edges of zGNRs, namely, z11, can be produced by C2H4 termination at mild experimental conditions, we quite wonder the magnetic and electronic properties of C2H4-zGNRs with z11 edge configuration. The same as H-zGNRs, our computations also revealed an AFM ground state for C2H4-8-zGNRs, which is 2 and 24 meV/edge atom lower in energy than the FM and NM states, respectively. For comparison, the AFM state of 8-H-zGNR is 2 and 26 meV/edge atom lower in energy than the FM and NM states, respectively.
Figure 3a presents the spatial distribution of the charge difference between α-spin and β-spin for 8-C2H4-zGNR. The magnetization per edge atom of C2H4-8-zGNR is 0.13 μB (0.15 μB for 8-H-zGNR), decaying gradually from two edges to the inner. Therefore, the stability and magnitude of edge magnetism of C2H4-zGNRs are comparable to those of H-zGNRs.
Then, we computed the band structure of 8-C2H4-zGNR in the AFM state. As shown in Figure 3b, 8-C2H4-zGNR has a 0.42 eV (0.45 eV for 8-H-zGNR) band gap for both spin channels. Especially, the spin-polarized π and π* bands are also quite flat near the Fermi level, a known symbol of edge states.
In lights of the above results, we conclude that C2H-zGNRs can well reproduce the electronic and magnetic properties of those H-zGNRs. Therefore, C2H4-zGNRs may realize many fancy properties previously predicted for H-zGNRs, such as half-metallicity13. Our computations demonstrated that under a 0.7 V/Å transverse electric field, 8-C2H-zGNR with z11 edge configuration can be tuned into half-metallic. Here note that generalized gradient approximation (GGA) usually predicts a much higher critical value of electric filed than local density approximation (LDA)42.
Discussion
Although we have determined that pure sp2 coordinated edges of zGNRs, namely, z11, can be produced by C2H4 termination at rather mild experimental conditions, there is an obvious question to be explained: why does z121 have a relatively large value of  and is unfavorable on the whole range of thermodynamics conditions? As revealed by Wassmann et al.34, z121 has the lowest value of
and is unfavorable on the whole range of thermodynamics conditions? As revealed by Wassmann et al.34, z121 has the lowest value of  among all the edge configurations of H-zGNRs and is stable in a rather boarder range of thermodynamic conditions. Then, what makes the difference for C2H4 and hydrogen terminations? Actually this difference is simply due to the steric effect of C2H4 molecules. As shown in Figure 1, in a unit cell of z121, two C2H4 molecules bond to an edge site of zGNR together to generate a sp3 edge site and the rest two carbon atoms of C2H4 molecules bond to two edge sites of zGNR to generate two sp2 edge sites. Due to the strong steric effect, two C2H4 molecules are pushed up and down, respectively, at the sp3 edge sites. Thus, the strain imposed on two sp2 edge sites causes a serious edge distortion (Figure S1 of supplementary information) and consequently increases the
among all the edge configurations of H-zGNRs and is stable in a rather boarder range of thermodynamic conditions. Then, what makes the difference for C2H4 and hydrogen terminations? Actually this difference is simply due to the steric effect of C2H4 molecules. As shown in Figure 1, in a unit cell of z121, two C2H4 molecules bond to an edge site of zGNR together to generate a sp3 edge site and the rest two carbon atoms of C2H4 molecules bond to two edge sites of zGNR to generate two sp2 edge sites. Due to the strong steric effect, two C2H4 molecules are pushed up and down, respectively, at the sp3 edge sites. Thus, the strain imposed on two sp2 edge sites causes a serious edge distortion (Figure S1 of supplementary information) and consequently increases the  . Here note that for z111122 and z1122, in which continuous two sp3 coordinated edge sites are present, the edge distortion is absent. Since z121 has the same C2H4 density (
. Here note that for z111122 and z1122, in which continuous two sp3 coordinated edge sites are present, the edge distortion is absent. Since z121 has the same C2H4 density ( ) as z111122 but a higher
) as z111122 but a higher  than z111122, z121 could never be the most stable edge configuration in any given value of
than z111122, z121 could never be the most stable edge configuration in any given value of  according to equation (2) and is hence excluded from the phase diagram.
according to equation (2) and is hence excluded from the phase diagram.
Besides the unstability problem of z121, there are still some concerns to be addressed. For example, for these stable edge configurations on the whole range of thermodynamic conditions, why are z11 and z22 magnetic while z1111122 and z1122 are nonmagnetic? Moreover, why does z11 have a rather low  , while z22 has a higher
, while z22 has a higher  than other stable edge configurations? Why does z111122 has an even lower
than other stable edge configurations? Why does z111122 has an even lower  than z11?
than z11?
The above concerns can be satisfactorily understood by the Clar's rule43,44, which has been successfully applied for accounting the π electron distribution and reactivity of polycyclic aromatic hydrocarbons (PAH)45,46,47 and many carbon nanomaterials48,49,50,51,52,53. According to the Clar's rule, the sp2 coordinated carbon atoms of a close-shell PAH can be formulated into two structural units that are linked by single bonds, benzenoid aromatic ring and olefinic double bond, wherever necessary. A PAH is the most stable when it has the greatest number of benzenoid rings. The unusual stability of graphene can be understood as all carbon atoms are benzenoid with a maxima density of benzenoid rings of 1/3. Without considering the steric effect of termination groups (as for H-terminated zGNRs), z121 should be the most stable edge configuration for zGNRs since it enables that zGNRs have the same density of benzenoid rings as graphene (Figure S2 of supplementary information). However, for C2H4-terminated zGNRs, the enhanced stabilization from aromaticity is overwhelmed by the steric effect; thus the z121 configuration is not favored anymore.
For zGNRs with density of benzenoid rings lower than 1/3, there is a competition between maximizing the density of benzenoid rings for the bulk and imposing unsaturated carbon atoms on the edges. Taking z11 of 8-C2H4-zGNR as an example, if we assume that all its carbon atoms are saturated with four chemical bonds with neighboring atoms, z11 will form the quinonoid structure with two double bonds in each hexagon (Figure S3 of supplementary information) and the formation of benzenoid ring in z11 is completely forbidden. However, the quinonoid structure is quite unstable. In this case, z11 would impose two unpaired electrons on each edge in a 1×1×3 supercell and the resulted nanoribbon has the same density of benzenoid rings (1/3) as graphene (Figure 4a). The energy gain from the resonance favors this electronic structure as the ground state. Therefore, z11 has a magnetic ground state with unpaired electrons on the edges. Moreover, the unpaired electrons of z11 have subtle hyperconjugation interactions with neighboring C = C bonds and C–H bonds of C2H4, which could stabilize the unpaired electrons (thus stabilizing the edge). Besides, there is also hyperconjugation interaction between C = C bonds and C–H bonds, which could also contribute to the stability of the edge. Thus, the multiple hyperconjugation interactions on the edge should be responsible for the rather favorable  of z11. In contrast, in H-zGNRs, there only exists the hyperconjugation interaction between unpaired electrons and C = C bonds, resulting in a larger
of z11. In contrast, in H-zGNRs, there only exists the hyperconjugation interaction between unpaired electrons and C = C bonds, resulting in a larger  for z(H)1 than z11.
for z(H)1 than z11.
Similarly, by imposing four unpaired electrons to the outer sp2 carbon atoms on each edge in a 1×1×3 supercell, the interior carbon atoms of z22 can also maximize the density of benzenoid rings (Figure 4b). In contrast to z11, only half of the unpaired electrons of z22 can have hyperconjugation interaction with C = C double bonds while the rest are localized. Such densely localized unpaired electrons on the edges result in a very high  for z22. These analyses can also explain why the magnetization of fully saturated edges of zGNRs is larger than the sp2 coordinated edges54.
for z22. These analyses can also explain why the magnetization of fully saturated edges of zGNRs is larger than the sp2 coordinated edges54.
In contrast to z11 and z22, z111122 can achieve the maximum density of benzenoid rings without imposing unpaired electron on the edge (Figure 4c). Moreover, z111122 can be further stabilized by the conjugation interaction between edge C = C double bonds. It is known that generally conjugation stabilization is stronger than hyperconjugation stabilization55,56. As a result, z111122 favors the nonmagnetic ground state and has a lower  than z11. For z1122, when the edge carbon atoms are all saturated, the inner carbon atoms can only be partially benzenoid (Figure 4d). However, imposing unpaired electron on edge cannot increase the number of benzenoid rings. Therefore, z1122 also favors the nonmagnetic ground state.
than z11. For z1122, when the edge carbon atoms are all saturated, the inner carbon atoms can only be partially benzenoid (Figure 4d). However, imposing unpaired electron on edge cannot increase the number of benzenoid rings. Therefore, z1122 also favors the nonmagnetic ground state.
Finally, an interesting question arises: is pure sp2 termination a guarantee for edge magnetism? Taking an example, like hydrogen and C2H4, C2H2 can only form single bonds with edge carbon atoms and intuitively may not disturb the π electron system of zGNR. Then, is C2H2, the dehydrogenation product of C2H4, also an ideal terminal group for zGNRs?
To address this concern, we investigated two edge configurations for C2H2 terminated 8-zGNRs (8-C2H2-zGNR), including z11 and z111122. In contrast to 8-C2H4-zGNR, z11 of 8-C2H2-zGNR (−0.205 eV/Å) has a lower  than z111122 (−0.196 eV/Å). Moreover, our computations revealed that both z11 and z111122 of 8-C2H2-zGNR have a nonmagnetic ground state. At first glance, this is rather surprising. The nonmagnetic z111122 of 8-C2H2-zGNR can be understood in the same away as discussed above for 8-C2H4-zGNR. However, why is z11 of 8-C2H2-zGNR also nonmagnetic? This seemingly unexpected result can also be understood by the competition between hyperconjugation, conjugation and maximizing benzenoid rings.
than z111122 (−0.196 eV/Å). Moreover, our computations revealed that both z11 and z111122 of 8-C2H2-zGNR have a nonmagnetic ground state. At first glance, this is rather surprising. The nonmagnetic z111122 of 8-C2H2-zGNR can be understood in the same away as discussed above for 8-C2H4-zGNR. However, why is z11 of 8-C2H2-zGNR also nonmagnetic? This seemingly unexpected result can also be understood by the competition between hyperconjugation, conjugation and maximizing benzenoid rings.
In contrast to the general intuition, C2H2 terminations significantly differ from C2H4 terminations, since C2H2 can couple to the π electron system of zGNR by forming double bonds with edge sites in the dominant resonance structure (Figure 5a): in a 1×1×3 supercell of z11 of 8-C2H2-zGNR, two C2H2 molecules each form two C-C single bonds with two edge sites in each edge, but the third C2H2 molecule forms two C = C bonds with two edge sites. With the help of newly formed C = C bonds, the carbon atoms of 8-C2H2-zGNR can achieve a density of benzenoid rings of 2/7 without imposing unpaired electron on the edge.
We can also get the resonance structure (Figure 5b) by imposing two unpaired electrons on each edge, in which the density of benzenoid rings can be increased to the maximum (1/3), the same as z11 of 8-C2H4-zGNR. However, this magnetic state is not favorable energetically since the conjugation in the nonmagnetic state overwhelms the energy gain by maximizing the benzenoid rings. In the nonmagnetic state, the C = C bonds at edges have conjugation interaction along the zigzag direction; in the magnetic state, there exists hyperconjugation interaction between unpaired electrons and neighboring C = C bonds. The much stronger conjugation stabilization in the nonmagnetic state over the hyperconjugation stabilization in the magnetic state overcompensates the unfavorability of the nonmagnetic state with fewer benzenoid rings, which leads to a nonmagnetic ground state.
Another question is why z11 8-C2H2-zGNR has a lower  than z111122. Note that z111122 has the same density of benzenoid rings as z11 and it also has the conjugation stabilization among edge C = C bonds (Figure S4 of supplementary information). However, the conjugation interaction in z111122 is not continuous in the zigzag direction while the conjugation interaction in z11 is continuous. Therefore, z111122 has a slightly lower
than z111122. Note that z111122 has the same density of benzenoid rings as z11 and it also has the conjugation stabilization among edge C = C bonds (Figure S4 of supplementary information). However, the conjugation interaction in z111122 is not continuous in the zigzag direction while the conjugation interaction in z11 is continuous. Therefore, z111122 has a slightly lower  than z11.
than z11.
Overall, though C2H2 termination can produce sp2 coordinated edges with energetically very favorable  , C2H2 can suppress the edge magnetism by coupling to the π-electron system of zGNR, which disqualifies C2H2 as an ideal terminal group for zGNRs. Therefore, even pure sp2 termination is not a guarantee for edge magnetism.
, C2H2 can suppress the edge magnetism by coupling to the π-electron system of zGNR, which disqualifies C2H2 as an ideal terminal group for zGNRs. Therefore, even pure sp2 termination is not a guarantee for edge magnetism.
To summarize, by means of DFT computations, we systemically studied the energetics and electronic properties of C2H4-zGNRs with different edge configurations. The pure sp2 coordinated edges, namely z11, can be stabilized at rather mild experimental conditions. Especially, such C2H4-zGNRs with sp2 edges can well reproduce the magnetic and electronic properties of H-zGNRs. Therefore, C2H4 is an ideal terminal group for zGNRs in terms of preserving the edge magnetism. Interestingly, the edge electronic structures of C2H4-zGNRs can be well interpreted by employing the Clar's rule. Further analysis identified multiple hyperconjugation interactions as the key factor responsible for enhanced stability of the sp2 coordinated edges. Moreover, we demonstrated that pure sp2 termination can not guarantee edge magnetism for zGNRs, for example, C2H2 termination can couple to the π-electron system of zGNRs and suppress the magnetism. These findings would deepen our basic knowledge of graphene electronics and provide a feasible way for realizing zGNR-based spintronics.
Methods
DFT computations were performed using the plane-wave technique implemented in Vienna ab initio simulation package (VASP)57. The ion-electron interaction is described using the projector-augmented plane wave (PAW) approach58,59. GGA expressed by PBE functional60 and a 400 eV cutoff for the plane-wave basis set were adopted in all computations. Self-consistent field (SCF) calculations were conducted with a convergence criterion of 10−4 eV on the total energy and the electron density. 1D periodic boundary condition (PBC) was applied along the z direction in order to simulate their infinitely long systems. The minimum distance between two ribbons is larger than 15 Å, which can safely avoid the interaction between two ribbons. The Brillouin zone was sampled with a 1×1×10 Γ centered k points. Based on the optimized geometric structures, 21 k-points were used to obtain the band structures.
References
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. U.S.A. 102, 10451–10453 (2005).
Novoselov, K. S. et al. A roadmap for graphene. Nature 490, 192–200 (2012).
Georgakilas, V. et al. Functionalization of graphene: covalent and non-covalent approaches, derivatives and applications. Chem. Rev. 112, 6156–6214 (2012).
Tang, Q., Zhou, Z. & Chen, Z. F. Graphene-related nanomaterials: tuning properties by functionalization. Nanoscale 5, 4541–4583 (2013).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett., 97, 216803 (2006).
Barone, V., Hod, O. & Scuseria, G. E. Electronic structure and stability of semiconducting graphene nanoribbons. Nano Lett. 6, 2748–2754 (2006).
Li, X. L., Wang, X. R., Zhang, L., Lee, S. W. & Dai, H. J. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science 319, 1229–1232 (2008).
Han, M. Y., Özyilmaz, B., Zhang, Y. & Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).
Fujita, M., Wakabayashi, K., Nakada, K. & Kusakabe, K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920–1923 (1996).
Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys. Rev. B 54, 17954–17961 (1996).
Wakabayashi, K., Sigrist, M. & Fujita, M. Spin wave mode of edge-localized magnetic states in nanographite zigzag ribbons. J. Phys. Soc. Jpn. 67, 2089–2093 (1998).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006).
Kan, E. J., Li, Z. Y., Yang, J. L. & Hou, J. G. Half-metallicity in edge-modified zigzag gaphene nanoribbons. J. Am. Chem. Soc. 130, 4224–4225 (2008).
Li, Y. F., Zhou, Z., Shen, P. W. & Chen, Z. Spin gapless semiconductor-metal-half-metal properties in nitrogen-doped zigzag graphene nanoribbons. ACS Nano, 3, 1952–1958 (2009).
Jiang, D. E., Sumpter, B. G. & Dai, S. Unique chemical reactivity of a graphene nanoribbon's zigzag edge. J. Chem. Phys. 126, 134701 (2007).
Okada, S. Energetics of nanoscale graphene ribbons: edge geometries and electronic structures. Phys. Rev. B 77, 041408 (2008).
Huang, B. et al. Quantum manifestations of graphene edge stress and edge instability: a first-principles study. Phys. Rev. Lett. 102, 166404 (2009).
Koshinen, P., Malola, S. & Häkkinen, H. Self-passivating edge reconstructions of graphene. Phys. Rev. Lett. 101, 115502 (2008).
Kastler, M., Schmidt, J., Pisula, W., Sebastiani, D. & Müllen, K. From armchair to zigzag peripheries in nanographenes. J. Am. Chem. Soc. 128, 9526–9534 (2006).
Cai, J. M. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Jiao, L. Y., Zhang, L., Wang, X. R., Diankov, G. & Dai, H. J. Narrow graphene nanoribbons from carbon nanotubes. Nature 458, 877–880 (2009).
Kosynkin, D. V. et al. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons. Nature 458, 872–876 (2009).
Jiao, L. Y., Wang, X. R., Diankov, G., Wang, H. & Dai, H. J. Facile synthesis of high-quality graphene nanoribbons. Nature Nanotechnol. 5, 321–325 (2010).
Campos-Delgado, J. et al. Bulk production of a new form of sp2 carbon: crystalline Ggraphene. Nano Lett. 8, 2773–2778 (2008).
Morelos-Gómez, A. et al. Clean nanotube unzipping by abrupt thermal expansion of molecular nitrogen: graphene nanoribbons with atomically smooth edges. ACS Nano. 6, 2261–2271 (2012).
Kobayashi, Y., Fukui, K., Enoki, T. & Kusakabe, K. Edge state on hydrogen-terminated graphite edges investigated by scanning tunneling microscopy, Phys. Rev. B 73, 125415 (2006).
Riter, K. A. & Lyding, J. W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nat. Mater. 8, 235–242 (2009).
Tao, C. et al. Spatially resolving edge states of chiral graphene nanoribbons. Nat. Phys. 7, 616–620 (2011).
Pan, M. et al. Topographic and spectroscopic characterization of electronic edge states in CVD grown graphene nanoribbons. Nano Lett. 12, 1928–1933 (2012).
Zhang, X. et al. Experimentally engineering the edge termination of graphene nanoribbons. ACS Nano. 7, 198–202 (2013).
Joseph Joly, V. L. et al. Observation of magnetic edge state in graphene nanoribbons. Phys. Rev. B 81, 245428 (2010).
Konishi, A. et al. J. Am. Chem. Soc. 135, 1430–1437 (2013).
Wassmann, T., Seitsonen, A. P., Saitta, A. M., Lazzeri, M. & Mauri, F. Structure, stability, edge states and aromaticity of graphene ribbons. Phys. Rev. Lett. 101, 096402 (2008).
Seitsonen, A. P., Saitta, A. M., Wassmann, T., Lazzeri, M. & Mauri, F. Structure and stability of graphene nanoribbons in oxygen, carbon dioxide, water and ammonia. Phys. Rev. B 82, 115425 (2010).
Chia, C.-I. & Crespi, V. H. Stabilizing the zigzag edge: graphene nanoribbons with sterically constrained terminations. Phys. Rev. Lett. 109, 076802 (2012).
Plasser, F. et al. The multiradical character of one- and two-dimensional graphene nanoribbons. Angew. Chem. Int. Ed. 52, 2581–2584 (2013).
Gao, L., Guest, J. R. & Guisinger, N. P. Epitaxial graphene on Cu(111). Nano Lett. 10, 3512–3516 (2010).
Martinez-Galera, A., Brihuega, I. & Gómez-Rodríguez, J. M. Ethylene irradiation: a new route to grow graphene on low reactivity metals. Nano Lett. 11, 3576–3580 (2011).
Koskinen, P., Malola, S. & Häkkinen, H. Evidence for Graphene Edges Beyond Zigzag and Armchair. Phys. Rev B 80, 073401 (2009).
Lide, D. R. CRC Handbook of chemistry and physics. (CRC, Boca Raton, 2008).
Li, Y., Zhou, Z., Shen, P. & Chen, Z. Electronic and magnetic properties of hybrid graphene nanoribbons with zigzag-armchair heterojunctions. J. Phys. Chem. C 116, 208–213 (2012).
Clar, E. Polycyclic hydrocarbons. (Academic Press: New York, 1964).
Clar, E. The aromatic sextet. (Wiley: London, 1972).
Watson, M. D., Fechtenkötter, A. & Müllen, K. Big is beautiful−“aromaticity” revisited from the viewpoint of macromolecular and supramolecular benzene chemistry. Chem. Rev. 101, 1267–1300 (2001).
Randic, M. Aromaticity of polycyclic conjugated hydrocarbons. Chem. Rev. 103, 3449–3606 (2003).
Popov, I. A. & Bolydrev, A. I. Chemical Bonding in Coronene, Isocoronene and Circumcoronene. Eur. J. Org. Chem. 3485–3491 (2012).
Wassmann, T., Seitsonen, A. P., Saitta, A. M., Lazzeri, M. & Mauri, F. Clar's theory, π-electron sistribution and deometry of graphene nanoribbons. J. Am. Chem. Soc. 132, 3440–3451 (2010).
Gao, X. F., Zhao, Y. L., Liu, B., Xiang, H. J. & Zhang, S. B. π-bond maximization of graphene in hydrogen addition reactions. Nanoscale. 4, 1171–1176 (2012).
Popov, I. A., Bozhenko, K. V. & Boldyrev, A. I. Is graphene aromatic? Nano Res. 5, 117–123 (2012).
Popov, I. A. & Boldyrev, A. I. Deciphering chemical bonding in a BC3 honeycomb epitaxial sheet. J. Phys. Chem. C 116, 3147–3152 (2012).
Popov, I. A. & Boldyrev, A. I. Chemical bonding in coronene, isocoronene and circumcoronene. Eur. J. Org. Chem. 2012, 3485–3491 (2012).
Li, Y. & Chen, Z. Patterned partially hydrogenated graphene (C4H) and its one-dimensional analogues: a computational study. J. Phys. Chem. C. 116, 4526–4534 (2012).
Kudin, K. N. Zigzag graphene nanoribbons with saturated edges. ACS Nano 2, 516–522 (2008).
Jarowski, P. D., Wodrich, M. D., Wannere, C. S., Schleyer, P. v. R. & Houk, K. N. How large is the conjugative stabilization of diynes? J. Am. Chem. Soc. 126, 15036–15038 (2004).
Fernández, I. & Frenking, G. Direct estimate of the strength of conjugation and hyperconjugation by the energy decomposition analysis method. Chem.–Eur. J. 12, 3617–3629 (2006).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev B 59, 1758–1775 (1999).
Perdew, J. P., Burke, L. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
Support by Department of Defense (Grant W911NF-12-1-0083) and NSF (Grant EPS-1010094) in the US and the 111 Project (B12015) in China is gratefully acknowledged. CRC acknowledges the financial support of NSF NSEC Center for Hierarchical Manufacturing Grant No. CHM - CMMI – 0531171.
Author information
Authors and Affiliations
Contributions
Z.C. conceived the initial idea of this research. Y.L. demonstrated the initial idea and collected all the data. Z.Z. and C.C. participated in the discussion. Y.L. and Z.C. drafted the paper and all coauthors revised the manuscript. Z.C. guided the work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Li, Y., Zhou, Z., Cabrera, C. et al. Preserving the Edge Magnetism of Zigzag Graphene Nanoribbons by Ethylene Termination: Insight by Clar's Rule. Sci Rep 3, 2030 (2013). https://doi.org/10.1038/srep02030
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02030
This article is cited by
-
Circumventing the stability problems of graphene nanoribbon zigzag edges
Nature Chemistry (2022)
-
Spin splitting of dopant edge state in magnetic zigzag graphene nanoribbons
Nature (2021)
-
On-surface synthesis of graphene nanoribbons with zigzag edge topology
Nature (2016)
-
Preserving the edge magnetism of graphene nanoribbons by iodine termination: a computational study
Theoretical Chemistry Accounts (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.