Abstract
In this report, we investigate dynamical robustness of a complex network to noise injected through one of its nodes. We focus on synchronization of coupled nonlinear systems and, as a special instance, we address the classical consensus protocol for linear integrators. We establish an exact closed-form expression of the synchronization error for the consensus protocol and an approximate result for chaotic units. While structural robustness is known to be significantly affected by attacks targeted to network hubs, our results posit that dynamical robustness is controlled by both the topology of the network and the dynamics of the units. We provide examples where hubs perform better or worse than isolated nodes.
Similar content being viewed by others
Introduction
Communication networks, transportation infrastructures and power grids are all subjected to failures that often involve a significant portion of the system despite the local nature of the initial fault. Thus, error and attack tolerance, cascading failures, and, in general, robustness of complex networks have been the body of intense research1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17.
To quantify network robustness, generally defined as the ability of the network to withstand accidental events, different measures have been proposed: conditional connectivity3, restricted connectivity4, super connectivity5, fault diameter6, expansion parameter7, isoperimetric number8 and natural connectivity9. Other measures of network robustness have been developed in the theoretical framework of statistical physics and percolation theory10,11,12,13. These efforts seek to elucidate the effect of the removal of a fraction of nodes (or links) on characteristic properties of a network, such as its diameter, largest component and efficiency.
Such investigations have demonstrated that topology is a determinant of robustness, whereby heterogeneous (scale-free) networks are highly robust against random attacks, which can instead severely impact homogenous networks. Nevertheless, targeted attacks to hubs of scale-free networks can dramatically affect network properties. Indeed, the collapse of the entire network can be caused by a single node whose failure propagates to neighboring nodes promoting cascading damages and avalanches14,15,16,17. This phenomenon is well explained by modeling the dynamics of flow redistribution on the network to unveil the mechanisms underlying the large breakdowns observed in real systems, such as the Internet or electrical power grids16,17.
Most of the existing studies deal with the robustness of the network structure and are based on the assumption that the failure of a node (or a fraction of nodes) is equivalent to a complete loss of its (their) functionalities. Here, we take a different approach to understand the effect of a partial malfunctioning on the dynamics of the network. This scenario is expected to be relevant for biological networks18, distributed sensors19 and, in general, complex systems composed of coupled dynamical units20. Notably, robustness with respect to the system dynamics has been recently investigated in21, where networks of diffusively coupled second-order periodic oscillators are considered and node failure is modelled as the inactivation of oscillations (quenching).
In this report, we study networks of identical coupled dynamical units (including chaotic oscillators) and elucidate on the effect of partial malfunctioning of a network node on synchronization. We model the phenomenon of node failure by injecting noise into the dynamics of a node. In particular, we consider a white Gaussian signal with zero-mean and variance σ2. Increasing the noise level, that is, σ2, the synchronization error increases and the units may eventually leave the basin of attraction for sufficiently strong noise. Our primary objective is to establish a mathematical framework for assessing dynamical robustness and investigating the complex interplay between network topology and node dynamics. We derive tractable expression for the synchronization error and introduce a novel network parameter, which allows to rank the nodes in terms of their impact on the network dynamical robustness. We analyze four representative dynamics for coupled dynamical systems and explore different network topologies to illustrate the proposed methodology and demonstrate that both the topology and the dynamics are determinants of node ranking.
Results
Evaluation of dynamical robustness to noise injection into a node
Here, we establish a mathematical framework for assessing dynamical robustness and investigating the interplay between network topology and node dynamics. In particular, we consider a network of N dynamical units, which synchronize in the absence of noise. Dynamical robustness is quantified through the synchronization error as a function of the noise variance. To compute such error, we first derive the (stochastic) dynamical equations of the transverse modes of the system. From these equations, we relate the synchronization error to the statistical properties of the transverse modes and, more in detail, to their joint moments. Based on the derived expression of the error, we then introduce a novel network parameter, which allows to rank the nodes in terms of their impact on the network dynamical robustness.
We consider a network of N dynamical units, described by the following coupled equations:

for i = 1, …, N, where  represents the state vector of the ith node, F the individual dynamics, κ the coupling coefficient, gij the ijth entry of the network Laplacian G and Hx the coupling function. The term η is a zero-mean Gaussian white noise of variance σ2 and
represents the state vector of the ith node, F the individual dynamics, κ the coupling coefficient, gij the ijth entry of the network Laplacian G and Hx the coupling function. The term η is a zero-mean Gaussian white noise of variance σ2 and  is a vector of zeros and ones that models how the noise influences the dynamics of a node. We hypothesize that the noise acts on a single node, say node h, so that ξi = 1 if i = h and ξi = 0 if i ≠ h.
is a vector of zeros and ones that models how the noise influences the dynamics of a node. We hypothesize that the noise acts on a single node, say node h, so that ξi = 1 if i = h and ξi = 0 if i ≠ h.
To study the effect of the noise intensity and injection site on the network synchronization, we suppose that the network synchronizes in the absence of the noise and evaluate the synchronization error with respect to the noise variance. We consider the following synchronization error:

where 〈·〉t indicates averaging with respect to t in a defined observation window. For a sufficiently large observation window and assuming the system to be ergodic, the error (see Methods) is rewritten as:

where E[·] is the expected value, T contains the right eigenvectors of the graph Laplacian G and yk for k = 2, …, N are the transverse modes (see Methods).
Now, we distinguish between a special case of synchronization, namely the classical consensus problem27, for which an exact formula of  is derived and the more general case of synchronization of chaotic units, for which an approximation of
is derived and the more general case of synchronization of chaotic units, for which an approximation of  is established.
is established.
We first consider a consensus problem, that is,  and F = 0. In this case (see Methods), E[ykyl] is given by:
and F = 0. In this case (see Methods), E[ykyl] is given by:

As expected,  in (3) is linear with respect to σ and both the network topology and the node dynamics are important in shaping the network dynamical robustness.
in (3) is linear with respect to σ and both the network topology and the node dynamics are important in shaping the network dynamical robustness.
We now consider the case of synchronization of chaotic units. To this aim, we rewrite the dynamical equations of the transverse modes (see Methods) in terms of the scaled Gaussian noise  (with zero mean and variance
(with zero mean and variance  and we numerically compute the evolution of the modes for each value of
and we numerically compute the evolution of the modes for each value of  and calculate
and calculate  as a function of σ.
as a function of σ.
Consistently with the consensus problem, numerical simulations show that  is proportional to
is proportional to  . Thus, we define the function
. Thus, we define the function  so that
so that  . Since the transverse modes only differ for the term αk = κγk, in the following we use the notation
. Since the transverse modes only differ for the term αk = κγk, in the following we use the notation  . Notably, for the consensus problem, such function reduces to 1/(αk + αl). In general,
. Notably, for the consensus problem, such function reduces to 1/(αk + αl). In general,  depends only on the node dynamics, the coupling function and the modality for which noise is injected into the node.
depends only on the node dynamics, the coupling function and the modality for which noise is injected into the node.
To quantify the effect of noise injected in the network at the hth node, we define the normalized quantity  , which takes the following general form:
, which takes the following general form:

Injection of noise in correspondence of nodes with small ρh leads to smaller synchronization error, compared to the case when noise is applied to nodes with large ρh. Hence, the network is more robust to noise injected at sites with low ρh. We remark that ρh depends on the topology of the network and on the dynamics of the unit. In contrast with structural robustness, which depends only on topology, we find that dynamics is an essential element of dynamical robustness.
Interplay of topology and dynamics
We illustrate the concept of dynamical robustness through some examples. We consider two types of networks, that is, scale-free (SF) and Erdos-Renyi (ER) networks and four different dynamics for the network units: a simple integrator, a Chua's circuit22, a Rossler's system23 and a Chen's system24 (see Methods). These systems are selected on the basis of an exhaustive analysis on a multitude of dynamical systems (not reported here) to highlight the salient features of dynamical robustness that are unveiled by our study. We first investigate the agreement between our theoretical arguments and numerical or experimental data and then analyse ρh for some networks with a large number of nodes.
We consider a SF and an ER network with N = 100 nodes and average degree equal to 2 (see29 and Methods). The coupling coefficient κ is chosen so that the networks synchronize in the absence of noise and κγ2 does not vary. We integrate equation set (1) and evaluate the synchronization error (2). As expected, we find that  is linear in σ and we define
is linear in σ and we define  to compare the theoretical results based on ρh with numerical findings based on δh.
to compare the theoretical results based on ρh with numerical findings based on δh.
In Fig. 1, we report ρh vs δh for both types of networks. The agreement between simulations and theoretical expectations is almost perfect; theoretical expectations correctly reproduce the ranking of nodes based on the network performance in the presence of noise. In fact, nodes can be equivalently ranked according to either the value of ρh or of δh.
ρh vs. δh for each of the N nodes of a ER network (a,b,c,d) and a SF network (e,f,g,h) with N = 100 and average degree equal to 2.
The dynamics of a unit is: (a)-(e) integrator; (b)-(f) Chua's circuit; (c)-(g) Rossler's system; and (d)-(h) Chen's system. The coupling coefficient is κ = 1 (a,e); κ = 18.38 (b); κ = 2.97 (c); κ = 45.93 (d); κ = 13.81 (f); κ = 1.73 (g); and κ = 34.54 (h).
Next, we compare theoretical expectations with a network of real electronic oscillators. The experimental setup is that described in25 and consists of a network of six Chua's circuits coupled according to the network topology shown in Fig. 2(a). Fig. 2(b) shows the comparison between ρh (theoretical expectation) and δh (experimental data) for each network node, demonstrating a very good agreement between theoretical and experimental results.
To offer some statistical relevance to the proposed method, we numerically analyze ρh for networks with a large number of nodes. In particular, we consider SF and ER networks with N = 1000 nodes and average degree equal to 2. Fig. 3 illustrates the results for four case studies. In panels (a,b,c,d), we display the value of ρh ordered in ascending order for a SF and an ER network. In panels (e,f,g,h), we display the degree of node h, labelled as kh, vs. ρh. The network dynamics are those of Fig. 1. SF networks demonstrate worse performance than ER networks for most of the nodes in the case of consensus and Chua's dynamics. Instead, in the case of Rossler's systems, the SF network performs better than the ER network with the exception of a small percentage of nodes, which are the network hubs. In the case of Chen's systems, the ER network performs better than the SF network for about half of the nodes.
Numerical results for networks with N = 1000 nodes: (a,b,c,d) ρh and (e,f,g,h) degree of node h (kh).
The dynamics of a unit is: (a)-(d) consensus; (b)-(e) Chua's circuit; (c)-(f) Rossler's system; and (d)-(h) Chen's system. The coupling coefficient κ is 1 for consensus; 14.45 and 16.22 for SF and ER networks of Chua's circuits; 1.81 and 2.03 for SF and ER networks of Rossler's systems; and 14.88 and 17.49 for SF and ER networks of Chen's systems.
Based on the premise that the precise ranking of the nodes in terms of dynamical robustness is dictated by ρh, we observe some general trends in the node ranking with respect to topological measures, such as the node degree. Specifically, for the consensus problem and for the network of Chua's circuits, we find that nodes with high degree have better robustness to noise as compared to nodes with low degree. On the contrary, for networks of Rossler's systems, the opposite holds, whereby nodes with low degree display better robustness to noise than nodes with high degree. In the case of Chen's systems, the correlation between kh and ρh is weaker. In fact, the nodes that display poor dynamical robustness are those with high degree. Yet, there are also several low degree nodes with limited performance as shown in panel (h).
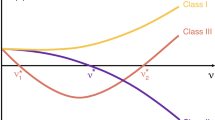
Our analysis demonstrates that robustness to noise is the result of the interplay between dynamics and topology, whereby dynamical robustness with respect to noise injected in select node cannot be inferred only on the basis of its degree or other topological measures such as, for instance, eigenvector centrality. To further elucidate this interplay, we report in Fig. 4 the function  for the different systems investigated. We distinguish between functions
for the different systems investigated. We distinguish between functions  that are monotonically decreasing with respect to each of their variables αk and αl and those that are not. Specifically, we define as
that are monotonically decreasing with respect to each of their variables αk and αl and those that are not. Specifically, we define as  the family of functions that are monotonically decreasing with respect to each of the two variables. Thus, for consensus and Chua's circuit
the family of functions that are monotonically decreasing with respect to each of the two variables. Thus, for consensus and Chua's circuit  , while for Rossler's and Chen's dynamics
, while for Rossler's and Chen's dynamics  We observe that this difference is crucial to determine the opposite behaviors found in the correlation between node degree and node robustness, for instance, for the Chua's circuit and the Rossler's system.
We observe that this difference is crucial to determine the opposite behaviors found in the correlation between node degree and node robustness, for instance, for the Chua's circuit and the Rossler's system.
The interplay between topology and dynamics in dynamical robustness can be further illustrated through the analysis of an exemplary network, which allows for the derivation of closed-form expressions. In particular, we focus on a star network topology for which we can find ρh for every network node. In this network, one node, labelled as node 1 and referred to as the hub, is connected to all the other nodes of the network, referred to as the leaves. All the leaves have degree equal to one, while the hub has degree N − 1. The star network Laplacian has eigenvalues equal to: γ1 = 0, γ2,…,N−1 = 1 and γN = N. For such network, lengthy, but trivial, calculations lead to the following formulas for ρ1 and ρ2,…,N:

These expressions are particularly simple since they depend only on two values of the function  , that is,
, that is,  and
and  . It is easy to note that ρ1 is greater than ρ2,…,N (that is, the leaves perform better than the hubs) if and only if
. It is easy to note that ρ1 is greater than ρ2,…,N (that is, the leaves perform better than the hubs) if and only if  . Given the form of
. Given the form of  for the Chen's system,
for the Chen's system,  can be either greater or lower than
can be either greater or lower than  , which implies that according to the values of α2 and αN (and, ultimately, on the coupling strength κ), the leaves can perform better than the hub or vice versa. This is illustrated in Fig. 5 for a star network of N = 5 Chen's systems. For κ = κ1 = 30, the hub of the network has superior dynamical robustness performance than peripheral nodes. In fact, κ1γ2 and κ1γN are such that
, which implies that according to the values of α2 and αN (and, ultimately, on the coupling strength κ), the leaves can perform better than the hub or vice versa. This is illustrated in Fig. 5 for a star network of N = 5 Chen's systems. For κ = κ1 = 30, the hub of the network has superior dynamical robustness performance than peripheral nodes. In fact, κ1γ2 and κ1γN are such that  (panel (a), black circles). Instead, for κ = κ2 = 60 the opposite holds,
(panel (a), black circles). Instead, for κ = κ2 = 60 the opposite holds,  (panel (a), red circles) and the leaves outperform the hub.
(panel (a), red circles) and the leaves outperform the hub.
(a) The function  for the Chen's system. (b-c)
for the Chen's system. (b-c)  vs. σ for a star network of N = 5 nodes for two different values of the coupling κ. In (b) (κ = 30), the hub of the network has better dynamical robustness performance than peripheral nodes. In (c) (κ = 60), the opposite holds.
vs. σ for a star network of N = 5 nodes for two different values of the coupling κ. In (b) (κ = 30), the hub of the network has better dynamical robustness performance than peripheral nodes. In (c) (κ = 60), the opposite holds.
The two cases correspond to a different location of the eigenvalues (κγ2,3,4 = κ and κγ5 = 5κ), leading to two different sets of values along the curve  marked in (a) as black (κ = 30) or red (κ = 60) circles. Note that h = 1 is the hub and h = 2, …, 5 are the leaves.
marked in (a) as black (κ = 30) or red (κ = 60) circles. Note that h = 1 is the hub and h = 2, …, 5 are the leaves.
The analysis of the star network confirms that, depending on the shape of  , the same topology may display opposite correlations between node degree and node robustness. In the general case (shown in Fig. 1(h)), for which
, the same topology may display opposite correlations between node degree and node robustness. In the general case (shown in Fig. 1(h)), for which  , a clear correlation between node degree and node robustness cannot be readily established.
, a clear correlation between node degree and node robustness cannot be readily established.
Discussion
Here, we have introduced a mathematical framework to understand the dynamical robustness of complex networks to noise injected into their nodes. The approach lends itself to the formulation of a novel performance metric, see Eq. (5), which allows for the quantification of dynamical robustness as a function of network topology and node dynamics. We have considered a spectrum of dynamics and topologies to demonstrate the complex response of networks to noise injection. In contrast with structural robustness, where attacks targeted to hubs are generally more severe than removal of low-degree nodes, injection of noise into hubs may be more or less dangerous than injection of noise into low-degree nodes depending on the unit dynamics. Experimental evidence of this second scenario has been reported for small networks (limited to up to six nodes) in25. A similar role of low-degree nodes has been also observed in21, where periodic oscillators have been considered and failure has been modelled through quenching rather than injected noise. Finally, we mention that another measure of network robustness in terms of the dynamical properties of the network has been introduced in30, where dynamic vulnerability, that is, the collective response of the network to a finite time perturbation into a single node, is studied for a network of Rossler's systems. The conclusion that the hubs are not the more vulnerable nodes is in agreement with our results.
We have found that networks of Chua's circuits and Rossler's systems are representative of two opposite behaviors that can be exhibited by a network in terms of its dynamical robustness to noise. Specifically, we have demonstrated that, in networks of Chua's circuits, the ranking of the nodes mirrors the node degree, while, in networks of Rossler's systems, low-degree nodes are more robust to noise injection. Furthermore, we have observed (as in the case of networks of Chen's systems) that there are scenarios in which a clear correlation between node degree and node robustness cannot be established. The different behaviors exhibited by these systems are explained by the shape of the function  in Eq. (5). For systems with
in Eq. (5). For systems with  , which we classify as dynamical robustness class I systems, we have observed a degree-correlated behavior (that is, higher degree nodes have higher dynamical robustness performance than lower degree nodes). On the other hand, for systems with
, which we classify as dynamical robustness class I systems, we have observed a degree-correlated behavior (that is, higher degree nodes have higher dynamical robustness performance than lower degree nodes). On the other hand, for systems with  , which we classify as dynamical robustness class II systems, a clear correlation between node degree and node robustness cannot be established. For dynamical robustness class II systems, different scenarios may arise depending on the system (topological and dynamical) parameters, including degree-correlated and anti-degree correlated behaviors. Thus, our main conclusion is that dynamical robustness is affected by both the topology of the network and the dynamics of the units and that the parameter ρh is a suitable measure for node dynamical robustness.
, which we classify as dynamical robustness class II systems, a clear correlation between node degree and node robustness cannot be established. For dynamical robustness class II systems, different scenarios may arise depending on the system (topological and dynamical) parameters, including degree-correlated and anti-degree correlated behaviors. Thus, our main conclusion is that dynamical robustness is affected by both the topology of the network and the dynamics of the units and that the parameter ρh is a suitable measure for node dynamical robustness.
Methods
Dynamical equations of transverse modes
Using the Kronecker algebra, Eqs. (1) can be rewritten in the compact form:

where x = [x1, x2, …, xN]T, Hx(x) = [Hx(x1), Hx(x2, …, Hx(xN)]T and Ξ = [ξ1, ξ2, …, ξN]T.
Due to the presence of the noise, the oscillators cannot synchronize, that is, the solution x1 = … = xN is not feasible. Thus, we define the synchronization error with respect to a virtually synchronous state s whose evolution proxies the individual node dynamics when the noise is uniformly distributed in the network:  . We now linearize Eq. (7) around the synchronous state s to obtain
. We now linearize Eq. (7) around the synchronous state s to obtain

where ζ = x − 1N ⊗ s,  is the vector of all ones, Jacobians are evaluated on the synchronous state and
is the vector of all ones, Jacobians are evaluated on the synchronous state and  . To study Eq. (8), we define a new set of state variables y = T−1 ⊗ Imζ, where T contains the right eigenvectors of the graph Laplacian G and Im is the identity matrix of order m. For the sake of simplicity, we suppose that the network is undirected so that G is symmetric and T−1 = TT. Since
. To study Eq. (8), we define a new set of state variables y = T−1 ⊗ Imζ, where T contains the right eigenvectors of the graph Laplacian G and Im is the identity matrix of order m. For the sake of simplicity, we suppose that the network is undirected so that G is symmetric and T−1 = TT. Since  , we have:
, we have:

where γk for k = 1, …, N are the ordered eigenvalues of G. For k = 1, γ1 = 0 and Tj1 = 1 for j = 1, …, N so that the variation along the synchronization manifold evolves independently of the injected noise being controlled by the Lyapunov exponents of the individual dynamics. For k = 2, …, N, Eqs. (9) represent the dynamical equations of the transverse modes. The noise injected into the hth node affects each transverse mode yk and is weighted by the term  .
.
The synchronization error (2) is now rewritten in terms of the transverse modes. In fact, since  (where
(where  is the average trajectory that can be approximated as
is the average trajectory that can be approximated as  ) and
) and  , the error (2) can be rewritten as:
, the error (2) can be rewritten as:

Now, we illustrate the form of the dynamical equations of the transverse modes and the expression of  for the two cases investigated (the classical consensus problem and the more general case of synchronization of chaotic units).
for the two cases investigated (the classical consensus problem and the more general case of synchronization of chaotic units).
For the consensus problem ( and F = 0), Eq. (9) becomes
and F = 0), Eq. (9) becomes

By noting that for a continuous-time system in the form:

with a1, a2 > 0 and η1 and η2 zero-mean Gaussian processes with variance σ1 and σ2, respectively,  28, E[ykyl] is given by
28, E[ykyl] is given by  .
.
In the case of synchronization of chaotic units, Eq. (9) is rewritten in terms of the scaled Gaussian noise  (with zero mean and variance
(with zero mean and variance  , that is,
, that is,

In this case,  is calculated from Eq. (13). In particular, we numerically integrate Eq. (13) with the Euler-Maruyama integration method, we compute the evolution of the modes for each value of
is calculated from Eq. (13). In particular, we numerically integrate Eq. (13) with the Euler-Maruyama integration method, we compute the evolution of the modes for each value of  and calculate
and calculate  as a function of σ.
as a function of σ.
Model equations
The network for the consensus problem is described by Eqs. (1) with m = 1,  , F(xi) = 0, Hx(xi) = xi and Hη = 1.
, F(xi) = 0, Hx(xi) = xi and Hη = 1.
The network of Chua's circuits is described by Eqs. (1) with m = 3, xi = [xi,1, xi,2, xi,3]T, Hx(xi) = [xi,1, 0, 0]T, Hη = [1, 0, 0]T and F(xi) given by

The parameters are chosen so that the Chua's circuit is chaotic in the double scroll regime: αC = 9, βC = 14.3, m0 = −1/7 and m1 = 2/7.
The network of Rossler's systems is described by Eqs. (1) with m = 3, xi = [xi,1, xi,2, xi,3]T, Hx(xi) = [0, xi,2, 0]T, Hη = [1, 0, 0]T and F(xi) given by

The parameters are chosen so that the Rossler's system is chaotic: aR = 0.2, bR = 0.2 and cR = 9. The Rossler's equations are scaled by a factor equal to 10 to make the time scale similar to that of the Chua's circuit.
The network of Chen's systems is described by Eqs. (1) with m = 3, xi = [xi,1, xi,2, xi,3]T, Hx(xi) = [0, xi,2, 0]T, Hη = [1, 0, 0]T and F(xi) given by

The following parameters have been chosen: aC = 35, bC = 8/3 and cC = 28. The Chen's equations are scaled by a factor equal to 0.5 to render the time scale similar to that of the other systems investigated.
Eqs. (1) are integrated with the Euler-Maruyama method for a window of duration equal to 2000 with a time step of 0.001 (which is a time step adequate for all the three dynamics investigated) and noise standard deviation σ in the range [0, 0.5] (with a step of 0.02). The synchronization error (2) is evaluated on the last 500 time units of the simulation.
The Master Stability Function
In our analysis, the coupling coefficient κ is chosen so that the network synchronizes in the absence of the noise. This selection is informed by the Master Stability Function (MSF)26.
According to this approach, a block diagonalized variational equation of the form  represents the dynamics of the system around the synchronization manifold. Here, γk is the h-th eigenvalue of G, h = 1, …, N and DF and DH are the Jacobian matrices of F and H computed at the synchronous state. Therefore, the blocks of the diagonalized variational equation differ from each other only for the term κγk. To investigate the synchronization properties with respect to different topologies, the variational equation is studied as a function of a generic eigenvalue α (for the sake of simplicity, we limit the discussion to the case of undirected networks, for which the Laplacian has real eigenvalues). This leads to the definition of the Master Stability Equation (MSE):
represents the dynamics of the system around the synchronization manifold. Here, γk is the h-th eigenvalue of G, h = 1, …, N and DF and DH are the Jacobian matrices of F and H computed at the synchronous state. Therefore, the blocks of the diagonalized variational equation differ from each other only for the term κγk. To investigate the synchronization properties with respect to different topologies, the variational equation is studied as a function of a generic eigenvalue α (for the sake of simplicity, we limit the discussion to the case of undirected networks, for which the Laplacian has real eigenvalues). This leads to the definition of the Master Stability Equation (MSE):  .
.
The maximum (conditional) Lyapunov exponent λmax of the MSE is studied as a function of α, thus obtaining the MSF, that is, Ω(α). Then, the stability of the synchronization manifold in a given network is evaluated by computing the eigenvalues γk (with k = 2, …, N) of the matrix G and studying the sign of Ω at the points αk = κγk. If for all eigenmodes with k = 2, …, N, Ω is negative, then the synchronous state is stable at the given coupling strength κ.
In the literature, systems with always positive Ω are referred to as type I MSF systems1; systems having Ω negative for α larger than a given constant are referred to as type II MSF systems1; and systems having Ω negative only in a compact interval, that is, Ω < 0 in [α1, α2], are referred to as type III MSF systems1.
All the systems investigated in this report have type II MSF so that our analysis is not biased by the MSF type.
Networks' construction
We consider Erdos-Renyi (ER) networks, that is, networks having a connectivity distribution (the probability that a given node has a given number of links) following a Poisson-like distribution and scale-free (SF) networks, that is, networks with a heterogeneous degree distribution (a power-law distribution). Both networks are generated by using the model reported in29. The model has a single tunable parameter which allows to interpolate between ER and scale-free SF networks as far as the degree distribution is concerned.
References
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Wang, X. F. & Chen, G. Complex networks: small-world, scale-free and beyond. IEEE Circ. Syst. Mag. 3, 6–20 (2003).
Harary, F. Conditional connectivity. Networks 13, 347–357 (1983).
Esfahanian, A. H. & Hakimi, S. L. On computing a conditional edge connectivity of a graph. Inf. Process. Lett. 27, 195–199 (1988).
Bauer, G. & Bolch, G. Analytical approach to discrete optimization of queuing-networks. Comput. Commun. 13, 494–502 (1990).
Krishnamoorthy, M. S. & Krishnamurthy, B. Fault diameter of interconnection networks. Comput. Math. Appl. 13, 577–582 (1987).
Alon, N. Eigenvalues and expanders. Combinatorica 6, 83–96 (1986).
Mohar, B. Isoperimetric numbers of graphs. J. Comb. Theory Ser. B 47, 274–291 (1989).
Wu, J., Barahona, M., Tan, R. & Deng, H. Robustness of random graphs based on graph spectra. Chaos 22, 043101-1-7 (2012).
Albert, R., Jeong, H. & Barabasi, A. -L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Resilience of the Internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 86, 3682–3685 (2001).
Moreno, Y., Gomez, J. B. & Pacheco, A. F. Instability of scale-free networks under node-breaking avalanches. Europhys. Lett. 58, 630–636 (2002).
Moreno, Y., Pastor-Satorras, R., Vazquez, A. & Vespignani, A. Critical load and traffic instabilities in scale-free networks. Europhys. Lett. 62, 292–298 (2003).
Crucitti, P., Latora, V. & Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 69, 045104-1-4 (2004).
Bakke, J. O. H., Hansen, A. & Kertesz, J. Failures and avanlanches in complex networks. Europhys. Lett. 76, 717–723 (2006).
Boccaletti, S., Latora, V. & Moreno, Y. Handbook on Biological Networks, World Scientific (2009).
Akyildiz, I. F., Su, W., Sankarasubramaniam, Y. & Cayirci, E. Wireless sensor networks: a survey. Computer Networks 38, 393–422 (2002).
Northrop, R. B. Introduction to Complexity and Complex Systems, CRC Press (2010).
Tanaka, G., Morino, K. & Aihara, K. Dynamical robustness in complex networks: the crucial role of low-degree nodes. Sci. rep. 2, 232–237 (2012).
Madan, R. Chua's Circuit: A Paradigm for Chaos, World Scientific Series on Nonlinear Science, Series B (1993).
Rossler, O. An Equation for Continuous Chaos. Phys. Lett. 57A, 397–398 (1963).
Chen, G. & Ueta, T. Yet another chaotic attractor. Int. J. Bifurcation Chaos Appl. Sci. Eng. 9, 1465–1466 (1999).
Buscarino, A., Fortuna, L., Frasca, M., Iachello, M. & Pham, V. T. Experimental investigation of the robustness to noise in synchronization of network motifs. Chaos 22, 043106-1-9 (2012).
Pecora, L. M. & Carrol, T. L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 80, 2109–2112 (1998).
De Lellis, P., di Bernardo, M., Garofalo, F. & Liuzza, D. Analysis and stability of consensus in networked control systems. Applied Mathematics and Computation 217, 988–1000 (2010).
Papoulis, A. & Pillai, S. U. Probability Random Variables and Stochastic Processes, McGraw Hill (2002).
Gomez-Gardenes, J. & Moreno, Y. From scale-free to Erdos-Rényi networks. Phys. Rev. E 73, 056124-1-7 (2006).
Gutierrez, R., del-Pozo, F. & Boccaletti, S. Node vulnerability under finite perturbations in complex networks. PLoS ONE 6, e20236-1-8 (2011).
Acknowledgements
M. Porfiri was supported by the National Science Foundation under Grant No. CMMI-0745753.
Author information
Authors and Affiliations
Contributions
A.B., L.V.G., M.P., L.F. and M.F. conceived and designed the research. M.F. and M.P. developed the theoretical analysis. A.B. and L.V.G. carried out the numerical simulations. A.B., L.V.G., M.P. and M.F. analyzed the data. A.B., L.V.G., M.P., L.F. and M.F. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Buscarino, A., Gambuzza, L., Porfiri, M. et al. Robustness to noise in synchronization of complex networks. Sci Rep 3, 2026 (2013). https://doi.org/10.1038/srep02026
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02026
This article is cited by
-
The sympathy of two pendulum clocks: beyond Huygens’ observations
Scientific Reports (2016)
-
Amplitude dynamics favors synchronization in complex networks
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





 for (a) consensus; (b) Chua's circuit; (c) Rossler's system; and (d) Chen's system.
for (a) consensus; (b) Chua's circuit; (c) Rossler's system; and (d) Chen's system.