Abstract
Amounts of empirical evidence, ranging from microbial cooperation to collective hunting, suggests public goods produced often nonlinearly depend on the total amount of contribution. The implication of such nonlinear public goods for the evolution of cooperation is not well understood. There is also little attention paid to the divisibility nature of individual contribution amount, divisible vs. non-divisible ones. The corresponding strategy space in the former is described by a continuous investment while in the latter by a continuous probability to contribute all or nothing. Here, we use adaptive dynamics in finite populations to quantify and compare the roles nonlinearity of public-goods production plays in cooperation between these two contribution mechanisms. Although under both contribution mechanisms the population can converge into a coexistence equilibrium with an intermediate cooperation level, the branching phenomenon only occurs in the divisible contribution mechanism. The results shed insight into understanding observed individual difference in cooperative behavior.
Similar content being viewed by others
Introduction
Evolutionary game theory is a basic and general mathematical tool for studying the emergence of cooperation, which mostly centers on the prisoner's dilemma game and the public goods game. The prisoner's dilemma game has been widely employed to elucidate the cooperation conundrum between individual and group interests through pairwise interactions1,2,3. However in many realistic situations ranging from cellular organisms to hunter business to national negotiations, group activities with multiple agents instead of two individuals are usually involved, where the public good is produced to non-exclusively benefit all group members irrespective of whether or not they have contributed to its production. Such group activities can be succinctly characterized by public goods games4,5,6,7,8,9.
In simplest public goods games, each player belonging to a community is provided with the same endowment and adopts one of two feasible actions, say full cooperation (contributing all) and full defection (contributing nothing). The sum of contributions collected from the community is augmented by an enhancement factor and then equally distributed among individuals in the community irrespective of their actions. It is clear that groups full of cooperators are better off than groups full of defectors, whereas a defector always outperforms a cooperator in any given mixed group. In this case, players pursuing their own immediate self-interest do harm groups' interest and thus a social dilemma arises.
So far, amounts of studies have investigated the evolutionary dynamics of simplest public goods games, where the production function, linking the average contribution of the group to the ultimate amount of public goods produced, is linear. However, nonlinear production functions are abundant ranging from microbes to high-advanced organism to human society10,11,12,13,14,15,16. For example, nonlinear production of public goods has been uncovered in both Myxococcus and an engineered Escherichia coli system10,11. Nonlinear relationships between carnivore hunting success and group size are revealed in many empirical studies12,13,14,15. In addition, sigmoid production functions are widely used in economics16, which accelerate at the beginning of production and then decelerate. The effect of nonlinear production functions on the evolutionary dynamics of public goods games deserves further and intensive investigations due to its ubiquity.
To date, public goods games adhering to nonlinear production functions are usually probed among binary strategy, all or nothing4,5,6,7,8. However, the continuous strategy may better capture the flexibility of behavior. One typical continuous strategy, termed the cooperative investment, represents the fraction of the endowment contributed. Obviously, it is reasonable for the divisible endowment, e.g., the time and effort spent in producing the public good. But when individuals ‘probabilistically’ change their contribution according to environments and risk orientation, it is natural to assume that a player performs his actions with a fixed probability, i.e., the cooperative probability that a player invests all and otherwise invests nothing. In fact, the cooperative investment and the cooperative probability can be envisaged as two different contribution mechanisms, both ubiquitous in real life. Nonetheless, their adaptive dynamics in finite populations remains unclear.
In this paper, we will compare the roles nonlinear production functions play in the evolution of both the cooperative investment and the cooperative probability in finite populations. Throughout, ρ(y, x) and p(y, x) separately represent the fixation probability and the payoff of a single mutant with y in a resident population that is monomorphic for x, x′(t) is the first-order derivative of x(t) with respect to t,  is the m-order partial derivative of f(y, x) with respect to y and
is the m-order partial derivative of f(y, x) with respect to y and  represents that y in
represents that y in  is replaced by x.
is replaced by x.
Results
Model description
Consider a population of size N, from which groups of size n are randomly chosen to play public goods games. Each individual is initialized with the same endowment (1 for simplicity), which is then allocated according to his strategy x ∈ [0, 1]. The strategy x may represent the amount of an individual contributing in a game. In this situation, x is the cooperative investment. In addition, the strategy x may as well indicate the probability that a player invests 1 and otherwise invests 0. At this time, x is the cooperative probability. The production function, describing the relationship between the average investment per person in a group and public goods produced, is denoted by g(s). Similar to games in economics9, the initial endowment is added to the payoff and the remaining function denoted by h(s) is used to describe the link between the investment and the remaining endowment (i.e., the initial endowment minus the cost incurred by his investment). The production function g(s) is assumed to increase satisfying g(0) = 0 and the remaining function h(s) decrease satisfying h(0) = 1 and h(1) = 0.
Comparison of two contribution mechanisms
The adaptive dynamics of the cooperative investment seems much different from that of the cooperative probability (see Supplementary Information). Nonetheless when linear production function g(s) and linear remaining function h(s) are used, the evolution of the cooperative investment exactly coincides with that of the cooperative probability, which is monotonic and yields no singular strategy. If nonlinear g(s) and nonlinear h(s) are adopted, the difference between the evolution of two contribution mechanisms becomes striking.
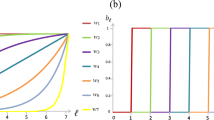
As to the cooperative investment, the adaptive dynamics with quadratic production and remaining functions generates at most one singular point, whereas that with cubic production and remaining functions yields at most two singular points. The corresponding examples are shown in figure 1: (a) A unique branching point x* = 0.5. The initially uniform population first converges to x* and subsequently splits into two clusters, one full of cooperators and the other full of defectors. (b) A unique CESS x* = 0.5. All individuals from an initially uniform population eventually contribute x* to the production of public goods. (c) A unique repeller x* = 0.5. Depending on the start-up strategy, the initially uniform population evolves to all cooperators or to all defectors. Owing to the co-occurrence of a repeller and a branching point in (d) and (e), whether the initially uniform population undergoes evolutionary branching is up to the initial strategy. The evolutionary branching forms a cooperator branch consisting of individuals contributing 1 and a defector branch consisting of individuals contributing 0. Due to the existence of the cooperator branch in (d) or the defector branch in (e), the repeller can not block the proceeding of the defector branch in (d) or the cooperator branch in (e). We note that the trajectory obtained by the Monte Carlo simulation is completely accordant with the “pairwise invasibility plot” (see Method for PIP).
The adaptive dynamics of the cooperative investment with varying production and remaining functions g(s) and h(s).
The left column shows the trajectories obtained by numerical simulations (see Supplementary Information), the middle column the PIP. The singular strategies (dashed horizonal lines) are indicated where appropriate. The right column shows the production function g(s) (increasing) and the remaining function h(s) (decreasing) accrued in homogeneous populations. (a) A branching point 0.5. (b) A CESS 0.5. (c) A repeller 0.5. (d and e) Two singular strategies; in (d), a branching point 0.67 along with a repeller 0.29; in (e), a branching point 0.31 together with a repeller 0.69. We adopt the fixation probability ρ(y, x) − ρ(x, x) as the ‘invasion fitness’ and perform a single simulation in (a) and two distinct simulations in (b)–(e). The abscissa ‘time’ represents the number of updating steps divided by 5 × 103. Parameters: n = 10, N = 100, σ = 0.00005, u = 0.01, (a) g(s) = −11s2 + 22s and h(s) = 0.8s2 − 1.8s + 1, (b) g(s) = s2 + 10s and h(s) = −s2 + 1, (c) g(s) = s2 + 10s and h(s) = s2 − 2s + 1, (d) g(s) = −s3 − 2.9s3 + 14.6s and h(s) = −0.1s3 + 0.54s2 − 1.44s + 1, (e) g(s) = s3 − 5.9s2 + 16.2s and h(s) = 0.1s3 + 0.25s2 − 1.35s + 1.
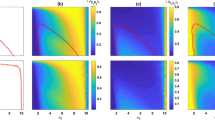
In contrast with the adaptive dynamics of the cooperative investment, all three types of singular points don't emerge but instead just the CESS and the repeller emerge from that of the cooperative probability17. The unique singular point coming from the adaptive dynamics with convex g(s) is a repeller (figure 2a) and the unique singular point from that with concave g(s) is a CESS (figure 2b). The evolutionary outcome induced by a unique repeller of the cooperative probability is exactly the same as that of the cooperative investment. However, a unique CESS of the cooperative probability statistically leads to the coexistence of cooperators and defectors. This is completely different from the evolutionary result induced by a unique CESS of the cooperative investment. The co-occurrence of a repeller and a CESS can be observed for sigmoid g(s) which is first convex and then concave (figure 2c) or inverse sigmoid g(s) which is first concave and then convex (figure 2d). Here, the trajectory obtained by the Monte Carlo simulation exhibits perfect agreement with the ‘PIP’.
The adaptive dynamics of the cooperative probability with varying production functions g(s).
The left column shows the trajectories obtained by numerical simulations (see Supplementary Information), the middle column the PIP. The singular strategies (dashed horizonal lines) are indicated where appropriate. The right column shows the production function g(s) accrued in homogeneous populations. (a) A repeller 0.67. (b) A CESS 0.35. (c and d) Two singular strategies; in (c), a CESS 0.73 along with a repeller 0.27; in (d), a CESS 0.16 together with a repeller 0.84. We adopt the fixation probability ρ(y, x) − ρ(x, x) as the ‘invasion fitness’ and perform two distinct simulation in (a and b) and three distinct simulations in (c) and (d). The abscissa ‘time’ represents the number of updating steps divided by 105. Parameters: N = 100, n = 10, σ = 0.00001, u = 0.01, (a) g(s) = 0 for 0 ≤ s < 1, g(s) = 3.5 for s = 1, (b) g(s) = 0 for s = 0, g(s) = 3.5 for 0 < s ≤ 1, (c) g(s) = 0 for s = 0, g(s) = 1.75 for 0 < s < 0.5, g(s) = 3.5 for s = 1, (d) g(s) = 0 for 0 ≤ s < 0.5, g(s) = 1.75 for s = 0.5, g(s) = 3.5 for 0.5 < s ≤ 1.
We illustrate the link between the adaptive dynamics of continuous strategy and the Markov process of binary strategy by considering local games between a strategy x and his nearby strategy x + σ (small σ). In a small population of size N, four types of selection scenarios may occur among two strategies: (i) selection favors x replacing x + σ but acts against x + σ replacing x (i.e.,  and
and  ), (ii) selection acts against x replacing x + σ but favors x + σ replacing x (i.e.,
), (ii) selection acts against x replacing x + σ but favors x + σ replacing x (i.e.,  and
and  ), (iii) selection favors both x replacing x + σ and x + σ replacing x (i.e.,
), (iii) selection favors both x replacing x + σ and x + σ replacing x (i.e.,  and
and  ), (iv) selection acts against x replacing x + σ and x + σ replacing x (i.e.,
), (iv) selection acts against x replacing x + σ and x + σ replacing x (i.e.,  and
and  ).
).
We here come to some conclusions for general adaptive dynamics (see Supplementary Information). If the strategy x is away from a singular strategy, the adaptive dynamics of x is directional and local game between x and x + σ is of either type (i) or type (ii). Furthermore if an attracting singular point emerges, of x and x + σ, the one closer to the attracting singular strategy replaces the other with a greater probability than the reverse situation. If x is a singular strategy, local games among two strategies x and x + σ can exhibit very rich evolutionary dynamics. A branching point and its nearby strategy must be favored by selection to replace each other and thus their local game is of type (iii). In contrast, local game between a CESS and its neighboring point may be of either type (i) or type (iv) in which selection acts against the CESS being replaced by its neighboring point. In addition, if x is a repeller, three generic games except type (i) can describe the evolutionary dynamics among two strategies x and x + σ.
In particular, all above four generic selection scenarios (i)–(iv) can appear in local games among two similar cooperative investment levels but just selection scenarios (i) and (ii) emerge in local games among two similar cooperative probability levels. In terms of the cooperative probability, local game between the CESS and its nearby strategy is only of type (i) and local game between the repeller and its neighboring point is only of type (ii). Moreover, the evolution of the cooperative probability can't result in a branching point. Since it is just local game between the singular point and his nearby point that can exhibit selection scenarios (iii) and (iv), evolutionary game dynamics described by type (iii) and type (iv) cannot appear in local games among two similar cooperative probability levels.
In large populations, we consider two types of adaptive dynamics, where the ‘invasion fitness’ is either p(y, x) − p(x, x) or ρ(y, x) − ρ(x, x) (see Supplementary Information). They exhibit consistence upon nonsingular points and their evolutionary direction. Further they display consistent convergence but inconsistent stability of a given singular point. From the view of the evolution of the cooperative probability, these two types of adaptive dynamics yield no inconformity. However, as to the cooperative investment, a branching point obtained by p(y, x) − p(x, x) may turn into a CESS if ρ(y, x) − ρ(x, x) is used.
Discussion
We consider the adaptive dynamics of both the cooperative investment and the cooperative probability in finite populations. In principle, the singular point, resulting from the evolution of the cooperative investment or the cooperative probability, seems to open up the possibility of a branching point, a CESS or a repeller. These three possibilities indeed occur in the adaptive dynamics of the cooperative investment, but it turns out that just either a repeller or a CESS exhibits in that of the cooperative probability.
Previous theoretical studies have examined the effect of nonlinear production functions on the evolutionary dynamics4,5,6,7,8,18,19. In contrast to our present model, some of previous models make a survey upon binary strategy4,5,6,7,8. Continuous strategy, however, can better capture the flexibility of behavior in real life. Therefore in our model, the adaptive dynamics of continuous strategy is investigated and is further connected with the evolutionary dynamics of binary strategy by considering local game among two similar strategies. In fact, some of previous models have probed the adaptive dynamics of the cooperative investment in infinitely large populations18,19. It is not a priori clear under which circumstances adaptive dynamics in infinitely large populations is a good approximation of the dynamics in a realistic system which is finite and subject to fluctuations. Unlike these models, we allow the population is finite and determine the adaptive evolution of the cooperative investment. A second set of previous models consider adaptive dynamics of the cooperative probability in not only infinite but also finite populations20,21,22. We note that they only apply to two-person games and involve no nonlinear benefit functions. In contrast with these models, we show how nonlinear production functions exert influence on the adaptive dynamics of the cooperative probability in public goods games.
Our work provides a natural explanation for the emergence of individual difference in cooperative behaviors (i.e., the amount of contribution varies from person to person). Individual variation in cooperative behaviors is ubiquitous among many species ranging from cellular microbes to high-advanced organisms to humans23,24,25,26,27,28,29. For example, social amoebaes communally form a fruiting body where spore cells selfishly promote their own reproduction at the cost of the stalk cells who are willing to sacrifice reproduction23. African lions and bottlenose dolphins do not all invest the same amount of energy but perform consistent different roles in the communal hunt24,25. In predator inspection, some individuals of three-spined sticklebacks, guppies and African lions lead the approach to the predator, whereas others lag behind26,27,28. In experimental economic games, participants differ in the amount of contribution29.
Our results show that there are two ways in which the stable co-occurrence of cooperators and defectors is maintained: (i) A branching point from the cooperative investment leads to evolutionary diversification from initially uniform populations to a stable state, where fixed proportion of the population contribute more consistently and the rest contribute less consistently. (ii) A CESS from the cooperative probability induces the initially uniform population to eventually reside in a stable state, in which all individuals randomly choose to contribute all or nothing with a fixed probability and thus generate the mix of cooperators and defectors. The former scenario generates consistent individual difference in cooperativeness and the latter yields non-consistent individual difference in cooperativeness. Although a great quantity of studies have investigated the emergence of consistent individual difference in behavior, few were proceeded under the framework of evolutionary game theory and and thus there have been calls to take into consideration such issues under the framework of evolutionary game theory30,31. Our results just have bridged the gap between individual difference in cooperative behaviors revealed in experimental findings and the adaptive dynamics in public goods games.
Methods
The powerful tool addressing the evolution of continuous strategy is the adaptive dynamics32, which says that the evolution of continuous strategy x on average takes the population up the gradient of ‘invasion fitness’ ζ(y, x), i.e.  (see the electronic supplementary material). The point satisfying η(x) = 0 is a singular strategy whose evolutionary direction needs close investigations upon η′(x) and
(see the electronic supplementary material). The point satisfying η(x) = 0 is a singular strategy whose evolutionary direction needs close investigations upon η′(x) and  33. The singular point x* is an attracting point in the sense that the initially uniform population converges to it if η′ (x*) < 0. In the opposite case, i.e., η′ (x*) > 0, the singular point is a repeller in that the initially uniform population evolves away from it and the bistable dynamics occurs. The subsequent fate of the attracting singular point x* is up to the sign of
33. The singular point x* is an attracting point in the sense that the initially uniform population converges to it if η′ (x*) < 0. In the opposite case, i.e., η′ (x*) > 0, the singular point is a repeller in that the initially uniform population evolves away from it and the bistable dynamics occurs. The subsequent fate of the attracting singular point x* is up to the sign of  . If
. If  , evolutionary branching emerges, where the initially uniform population splits into two strategic clusters after it converges to x*. Otherwise, the attracting point x* is a convergent evolutionary stable strategy (CESS) in the sense that the population remains at x* after it approaches infinitely to or reach x*.
, evolutionary branching emerges, where the initially uniform population splits into two strategic clusters after it converges to x*. Otherwise, the attracting point x* is a convergent evolutionary stable strategy (CESS) in the sense that the population remains at x* after it approaches infinitely to or reach x*.
As a convenient graphical means to indicate the sign of ζ(y, x) − ζ(x, x) for all possible values of x and y, we use the “pairwise invasibility plot” (PIP) where the horizontal axis is the resident strategy x and the vertical axis is the mutant strategy y. In PIP, the region with ζ(y, x) − ζ(x, x) > 0 is marked by ‘+’, the region with ζ(y, x) − ζ(x, x) < 0 is marked by ‘−’ and the intersection of the diagonal with another line on which ζ(y, x) = ζ(x, x) corresponds to the singular strategy. If the singular point x* is an attracting point, in PIP, there is a ‘+’ region above the diagonal on the left and below the diagonal on the right of x*. If the singular point x* is evolutionary stable, in PIP, the vertical line through x* lies completely inside a ‘−’ region,
References
Fu, F., Tarnita, C. E., Christakis, N. A., Wang, L., Rand, D. G. & Nowak, M. A. Evolution of in-group favoritism. Sci. Rep. 2, 460 (2012).
Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004).
Wu, T., Fu, F. & Wang, L. Moving away from nasty encounters enhances cooperation in ecological prisoner's dilemma game. PLoS ONE 6, e27669 (2011).
Bach, L. A., Helvik, T. & Christiansen, F. B. The evolution of n-player cooperation – threshold games and ESS bifurcations. J. Theor. Biol. 238, 426–434 (2006).
Hauert, C., Michor, F., Nowak, M. A. & Doebeli, M. Synergy and discounting of cooperation in social dilemmas. J. Theor. Biol. 239, 195–202 (2006).
Pacheco, J. M., Santos, F. C., Souza, M. O. & Skyrms, B. Evolutionary dynamics of collective action in N- person stage hunt dilemmas. Proc. R. Soc. B 276, 315–321 (2009).
Souza, M. O., Pacheco, J. A. & Santos, F. C. Evolution of cooperation under N-person snowdrift games. J. Theor. Biol. 260, 581–588 (2009).
Archetti, M. & Scheuring, I. Coexistence of cooperation and defection in public goods games. Evolution 65, 1140–1148 (2011).
Eldakar, O. T. & Wilson, D. S. Selfishness as second-order altruism. Proc. Natl Acad. Sci. USA 105, 6982–6986 (2008).
Chuang, J. S., Rivoire, O. & Leibler, S. Cooperation and Hamilton's rule in a simple synthetic microbial system. Mol. Syst. Biol. 6, 398 (2010).
Smith, J., van Dyken, J. D. & Zee, P. C. A generalization of Hamilton's rule for the evolution of microbial cooperation. Science 328, 1700–1703 (2010).
Packer, C. & Ruttan, L. The evolution of cooperative hunting. Am. Nat. 132, 159–198 (1988).
Kim, K. W., Krafft, B. & Choe, J. C. Cooperative prey capture by young subsocial spider I. Functional value. Behav. Ecol. Sociobiol. 59, 92–100 (2005).
Boesch, C. Cooperative hunting in wild chimpanzees. Anim. Behav. 48, 653–667 (1994).
MacNulty, D. R., Smith, D. W., Mech, L. D., Vucetich, J. A. & Packer, C. Nonlinear effects of group size on the success of wolves hunting elk. Behav. Ecol. 23, 75–82 (2011).
Heckathorn, D. D. The dynamics and dilemmas of collective action. Am. Sociol. Rev. 61, 250–277 (1996).
Zhang, Y. L., Wu, T., Chen, X. J., Xie, G. M. & Wang, L. (in press). Mixed strategy under generalized public goods games. J. Theor. Biol. (2013).
Doebeli, M., Hauert, C. & Killingback, T. The evolutionary origin of cooperators and defectors. Science 306, 859–862 (2004).
Cornforth, D. M., Sumpter, D. J. T., Brown, S. P. & Brännström, Å. Synergy and group size in microbial cooperation. Am. Nat. 180, 296–305 (2012).
Nowak, M. & Sigmund, K. The evolution of stochastic strategies in the prisoner's dilemma. Acta Appl. Math. 20, 247–265 (1990).
Hofbauer, J. & Sigmund, K. Adaptive dynamics and evolutionary stability. Appl. Math. Lett. 3, 75–79 (1990).
Imhof, L. A. & Nowak, M. A. Stochastic evolutionary dynamics of direct reciprocity. Proc. R. Soc. B 277, 463–468 (2010).
Fortunato, A., Strassmann, J. E., Santorelli, L. & Queller, D. C. Co-occurrence in nature of different clones of the social amoeba, Dictyostelium discoideum. Mol. Ecol. 12, 1031–1038 (2003).
Stander, P. E. Cooperative hunting in lions: the role of the individual. Behav. Ecol. Sociobiol. 29, 445–454 (1992).
Gazda, S. K., Connor, R. C., Edgar, R. K. & Cox, F. A division of labour with role specialization in group-hunting bottlenose dolphins (Tursiops truncatus) off Cedar Key, Florida. Proc. R. Soc. B 272, 135–140 (2005).
Milinski, M. TIT FOR TAT in sticklebacks and the evolution of cooperation. Nature 325, 433–435 (1987).
Heinsohn, R. & Packer, C. Complex cooperative strategies in group-territorial African lions. Science 269, 1260–1262 (1995).
Bleakley, B. H., Martell, C. M. & Brodie III, E. D. Variation in anti-predator behavior among five strains of inbred guppies, Poecilia reticulata. Behav. Genet. 36, 783–791 (2006).
Milinski, M., Sommerfeld, R. D., Krambeck, H.-J., Reed, F. A. & Marotzke, J. The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proc. Natl Acad. Sci. USA 105, 2291–2294 (2008).
Bergmüller, R., Johnstone, R. A., Russell, A. F. & Bshary, R. Integrating cooperative breeding into theoretical concepts of cooperation. Behav. Process. 76, 61–72 (2007).
McNamara, J. M., Stephens, P. A., Dall, S. R. X. & Houston, A. I. Evolution of trust and trustworthiness: social awareness favours personality differences. Proc. R. Soc. B 276, 605–613 (2009).
Allen, B., Nowak, M. A. & Dieckmann, U. Adaptive dynamics with interaction structure. Am. Nat. 181, E139–E163 (2013).
Geritz, S. A. H., Metz, J. A. J., Kisdi, É. & Meszéna, G. Dynamics of adaptation and evolutionary branching. Phys. Rev. Lett. 78, 2024–2027 (1997).
Acknowledgements
We are grateful for support from the National Natural Science Foundation of China (NSFC, No. 60774089, 10972003, 10926195).
Author information
Authors and Affiliations
Contributions
Y.Z., F.F., G.X. and L.W. devised the model. T.W. made simulations. Y.Z., F.F., T.W., G.X. and L.W. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
A tale of two contribution mechanisms for nonlinear public goods supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Zhang, Y., Fu, F., Wu, T. et al. A tale of two contribution mechanisms for nonlinear public goods. Sci Rep 3, 2021 (2013). https://doi.org/10.1038/srep02021
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02021
This article is cited by
-
Extinction scenarios in evolutionary processes: a multinomial Wright–Fisher approach
Journal of Mathematical Biology (2023)
-
On inferring evolutionary stability in finite populations using infinite population models
Journal of Mathematical Biology (2021)
-
Cooperation in group-structured populations with two layers of interactions
Scientific Reports (2015)
-
Swarm intelligence inspired shills and the evolution of cooperation
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.