Abstract
Transformation optics has shaped up a revolutionary electromagnetic design paradigm, enabling scientists to build astonishing devices such as invisibility cloaks. Unfortunately, the application of transformation techniques to other branches of physics is often constrained by the structure of the field equations. We develop here a complete transformation method using the idea of analogue spacetimes. The method is general and could be considered as a new paradigm for controlling waves in different branches of physics, from acoustics in quantum fluids to graphene electronics. As an application, we derive an “analogue transformation acoustics” formalism that naturally allows the use of transformations mixing space and time or involving moving fluids, both of which were impossible with the standard approach. To demonstrate the power of our method, we give explicit designs of a dynamic compressor, a spacetime cloak for acoustic waves and a carpet cloak for a moving aircraft.
Similar content being viewed by others
Introduction
Together with metamaterial science, transformation optics has dramatically improved our control over the manipulation of electromagnetic waves. This technique provides a way to know the properties that a medium should have in order to curve light propagation in almost any desired way. As a consequence, it has allowed for the creation of optical devices that were unthinkable only a decade ago1,2,3,4,5,6,7,8,9.
Transformation optics is standardly described as relying on the form-invariance of Maxwell's equations1,3,4,5,6,7, i.e., the fact that they have the same structure in any coordinate system10. In particular, the electromagnetic equations of a (virtual) medium MV using a distorted (non-Cartesian) set of coordinates SD are formally equal to those of a different (real) medium MR in Cartesian coordinates SC. For instance, if the virtual medium is homogeneous and isotropic, it will be non-diffractive. Then, the equivalence {MV, SD} ~ {MR, SC} allows us to design real media that are highly non-trivial (in general, inhomogeneous and anisotropic), but nevertheless retain the non-diffractive property.
Inspired by the success of transformation optics, scientists have tried to apply a similar procedure in other branches of physics, such as acoustics11,12,13,14 or quantum mechanics15. In these attempts, form-invariance seems to be the conditio sine qua non: without this property, a coordinate transformation cannot be reinterpreted as a certain medium. In many cases, the equations under consideration are form-invariant only under a certain subset of transformations, limiting the technique to this subset. For instance, the acoustic equations are not invariant under general transformations that mix space and time, so one cannot use transformation techniques to design devices such as time cloaks16,17 or frequency converters18. Here, we show that in many cases there is a way to escape this limitation and we fully develop the example of the acoustic wave equation. Let us first describe the proposal step by step in general terms.
Results
Consider a formal class of continuous physical systems described by two sets of fields: some parameter fields (e.g. permittivity and permeability), which describe a background medium and some dynamical fields Φ (e.g. electric and magnetic fields), describing some specific behavior on top of the background medium which we want to manipulate in our laboratory through transformation techniques. Thus, we call laboratory space the world where these fields exist. We assume that all these systems are described using the same standard Cartesian coordinate system SC = (t, x). In this way, different parameter fields always correspond to different media. In addition, imagine that the Φ-equations are not form-invariant under the desired transformations and therefore we cannot directly apply the traditional transformation paradigm as in optics.
The transformation method we propose entails as an essential prerequisite the existence of an auxiliary abstract relativistic system (we use “relativistic” in the General Relativity sense of form-invariance under any spacetime coordinate transformation) which is analogue to (i.e., possesses the same mathematical structure as) the relevant systems in laboratory space in at least one laboratory coordinate system (e.g., Cartesian). There is no need for the analogue model to have any direct physical meaning. In fact, this procedure is the exact reverse of what is done in the “analogue gravity” programme19: there, one searches for laboratory analogues of relativistic phenomena, e.g. in the quest to simulate Hawking radiation; here, one searches for relativistic analogues of laboratory phenomena (note that the exact relation between the original laboratory system and the auxiliary relativistic system is a subtle issue which has been studied in quite some detail in the literature on analogue gravity. See e.g. ref. 20,21). In the relativistic analogue, the geometric coefficients (typically, the coefficients of the metric tensor gμν) play the role of parameter fields; we will denote them generically by the letter C. For the laboratory coordinate systems for which the analogy holds, one specific system in laboratory space is mapped to one relativistic system written in an abstract coordinate system SAC = (t, x) (same coordinate labels as SC).
Once we find the analogue model, the method develops as follows (see Fig. 1):
-
Identify a simple (and probably idealized) virtual medium MV in laboratory space which possesses some physical or technological quality of interest (Step 1 in Fig. 1).
-
Map the laboratory equation associated with MV to its analogue equation in the abstract spacetime written in coordinates SAC (Step 2). The geometric coefficients CC(t, x) in these coordinates will be functions of the parameter fields of MV.
-
Express the analogue equation in a transformed set of coordinates
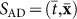 using the transformation f: SAC → SAD that encodes the desired distortion. One can apply any transformation one likes since the relativistic equations always maintain their form. This yields a new functional form for the geometric coefficients
using the transformation f: SAC → SAD that encodes the desired distortion. One can apply any transformation one likes since the relativistic equations always maintain their form. This yields a new functional form for the geometric coefficients 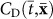 . Then, rename the new coordinates
. Then, rename the new coordinates 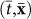 to (t, x).
to (t, x). -
Map the renamed equation back to laboratory space and obtain the new medium MR associated with CD(t, x) (Step 5). In MR, the change induced by f is “real”, i.e., the solutions in medium MR are related to those in medium MV by this transformation f.
Flowchart of the proposed analogue transformation method.
In the case of acoustics, the laboratory equations correspond to equation (2), which is not form-invariant, while the equations in abstract spacetime correspond to equation (3). The latter is form-invariant under any spacetime transformation (only the values of the metric components change depending on the coordinate system).
The reason why medium MR induces the desired change is that the solutions of the renamed equation (Step 4) are related to those of the original analogue equation (Step 2) by f. Since the solutions of the equations in Steps 1 and 2 and Steps 4 and 5 are identical, this correspondence is mapped to laboratory space, i.e., the solution  associated to medium MR is the desired distorted version of the solution Φ associated with medium MV. The advantage of the analogue method proposed here is that the transformation approaches can now be based on any symmetry that leaves the form of the analogue equations invariant in the abstract spacetime, rather than the restricted set which corresponds to the original equations in laboratory space. Since we ultimately map back to the original laboratory coordinates SC (step 5), it is guaranteed that we will also recover the original laboratory wave equation.
associated to medium MR is the desired distorted version of the solution Φ associated with medium MV. The advantage of the analogue method proposed here is that the transformation approaches can now be based on any symmetry that leaves the form of the analogue equations invariant in the abstract spacetime, rather than the restricted set which corresponds to the original equations in laboratory space. Since we ultimately map back to the original laboratory coordinates SC (step 5), it is guaranteed that we will also recover the original laboratory wave equation.
As in any transformational approach, the medium MR must be flexible enough to endow the laboratory equation with sufficient degrees of freedom (through flexible parameter fields) to reproduce the values of CD associated with the transformations of interest. This will typically require that the system includes moving media and metamaterials.
Let us now apply our new method to acoustics. The standard approach to transformation acoustics (STA) is based on the wave equation for the pressure perturbations p of a fluid medium

Here, B is the bulk modulus and ρij the anisotropic inverse matrix density of the background fluid. We use latin spatial indices (i, j) and Greek spacetime indices (μ, ν, with x0 = t). B and ρij are the parameter fields, while p is the dynamical field. From the transformational physics point of view, equation (1) has a set of drawbacks. i) Clearly, its form is non-invariant under coordinate transformations that mix space and time. ii) It cannot deal with fluids flowing with a non-zero background velocity, which however is the case in many interesting physical situations. iii) To derive equation (1), a necessary assumption is that the background (static) pressure is homogeneous22. Thus, it cannot be used for fluids with significant pressure gradients, such as when gravitational forces are relevant. iv) Three-dimensional transformations that require a local increase of the speed of sound in MR, also require an increase of its density. This is difficult to achieve with current metamaterials in airborne sound23,24.
The proposed method aims in the first place at overcoming the first drawback. Rather than starting from equation (1), one can look at the field of analogue gravity, where the formulation of a form-invariant equation has become a standard procedure. In terms of the velocity potential φ (the velocity perturbation is then vp = ∇φ), the equation for the acoustic perturbations of a barotropic and irrotational fluid is written as19,20,25

with ρ the mass density, c the speed of sound and v the fluid background velocity. This apparently innocent reformulation will already turn out to have several important side-benefits. However, so far, this equation is still not form-invariant under transformations that mix space and time. Therefore, we now apply one of the crucial insights of analogue gravity: equation (2) is structurally identical to the equation describing a relativistic massless scalar field over a curved spacetime19

with the (acoustic) metric

and g the metric determinant. Note that in this definition the choice of units can be considered irrelevant (see Supplementary Information). Equation (3) retains its form upon any coordinate transformation. Thus, using equation (2) as the laboratory equation and equation (3) as the analogue equation, we can apply the proposed procedure. The virtual medium MV in step 1 of Fig. 1 will be characterized by some parameters ρV, cV and vV and the real medium MR in step 5 by other parameters ρR, cR and vR. According to equation (3), the coefficients CC associated with MV are  , with equation (4) particularized for ρV, cV and vV. After applying all steps in Fig. 1, one obtains the relation between the parameter fields of MV and the new medium MR that reproduces the effect of the coordinate change.
, with equation (4) particularized for ρV, cV and vV. After applying all steps in Fig. 1, one obtains the relation between the parameter fields of MV and the new medium MR that reproduces the effect of the coordinate change.
As a result, many interesting transformations that involve mixing space and time, which could not be addressed in STA, now become possible (for instance, all those that mix time with one spatial variable – see Supplementary Information). A specific example consists of a time-dependent compression of space which acts only inside a three-dimensional box (the compressor). Such a compressor could be used, for instance, to select which rays are absorbed by a static omnidirectional absorber placed inside the box. The simulated performance of a specific configuration of the compressor-absorber device is shown in Fig. 2 (see the Methods section and the Supplementary Information for simulation details). It is based on the transformation  and
and  . According to the proposed method, this transformation can be implemented by a set of parameters given by cR/cV = ρV/ρR = f0(t) and
. According to the proposed method, this transformation can be implemented by a set of parameters given by cR/cV = ρV/ρR = f0(t) and  , with g(r, t) = r∂tf0(t) and
, with g(r, t) = r∂tf0(t) and  being the position vector. Both f0(t) and g(r, t) (normalized to cV) are depicted in Fig. 2.
being the position vector. Both f0(t) and g(r, t) (normalized to cV) are depicted in Fig. 2.
Time-dependent spatial compressor and omnidirectional absorber.
The absorber has a spherical shape with radius R = 0.29 m and is characterized by a static refractive index (relative to the background medium surrounding the compressor) given by n = 0.5R/r. The trajectories of two acoustic rays are simulated. After Ray 1 enters the box, the compression starts, according to the compression function f0(t). Ray 1 approaches the absorber, which traps it. Ray 2 feels no compression since f0(t) = 1 during the time it goes through the box. Thus, Ray 2 follows a straight line. See Supplementary Information for more details. (a) Simulated acoustic rays. (b) Compression function f0(t). (c) Function g(r, t).
Another example is the acoustic counterpart of the spacetime cloak reported recently for electromagnetic waves16. Unlike static invisibility cloaks, this device conceals only a certain set of spacetime events occurring during a limited time interval. To show how the proposed method allows for designing an acoustic spacetime cloak, we consider the transformation given by equations (20)–(23) in Ref. 16 (the transformation can also be found in the Supplementary Information). This transformation mixes time with one spatial variable. Therefore, the material parameters associated with the cloak can be obtained by substituting the mentioned transformation into equations (58)–(60) of the Supplementary Information. The resulting parameters are shown in Fig. 3. A set of acoustic rays propagating through such a medium were simulated and compared to the expected trajectories, finding an excellent agreement (see Fig. 3).
Acoustic spacetime cloak.
(a) Simulated acoustic rays. As can be seen, sound propagation is speeded up or slowed down in order to hide any acoustic event belonging to the cloaked region. Rays exit the cloak as if they had just passed through the background fluid. (b) Sound speed and (c) background velocity  of the cloak.
of the cloak.
As a side-benefit of the above procedure, we have automatically solved the other main drawbacks associated to equation (1): equations (2) and (3) do not require the background configuration to be of constant pressure and can deal with non-zero velocity background flows, making them much more generally applicable. Thus, we can now for example perform transformation acoustics with waves propagating in moving fluids, a common situation in aeronautics. Imagine, for instance, that we want to cloak a bump in an aircraft. In general, if the aircraft is moving with respect to the surrounding air, a traditional static cloaking device26,27 will fail to cloak the bump properly, because STA does not take into account that the background fluid velocity vR must also be adapted suitably. Instead, the proposed analogue transformation method allows us to obtain the required transformation of vR (see Fig. 4). Nonetheless, although we have theoretically solved the problem, the actual realization of the cloaking device should take into account other issues like, for example, aerodynamic constraints. It is worth mentioning that the designed carpet cloak does not introduce reflections, since the employed transformation is continuous at the boundaries. To further verify this fact, we calculated in COMSOL the ratio between the acoustic intensity (power) reflected to the left by the carpet cloak (Ir) and the intensity of the input wave (Ii), finding a value of Ir/Ii ≈ 10−4 (within numerical error). Note that, because one has a moving background, a Doppler effect on the acoustic wave is expected. This effect appears, however, equally in presence and absence of the carpet cloak, which does not further contribute to the evolution of the acoustic signal. The acoustic wave outside the carpet cloak is exactly the same as in the case in which it impinges onto a flat wall without carpet cloak. Thus, the frequency of the transmitted wave (i.e., reflected upwards by the wall with the bump surrounded by the cloak) is the same as the frequency of the input wave. Also note that the actual cloak will be made up of a certain microstructure that mimics the required density and sound speed. In general, the system bump-cloak will modify the original background velocity. However, the bump will be perfectly cloaked only if the background velocity is modified in a very specific way (the one corresponding to Fig. 4c) by this system. Any other background velocity will produce diffraction and thus static cloak designs cannot account for this situation. Since we are not considering any particular microstructure, as a simple example we have depicted in Fig. 4b the case in which the bump-cloak system is assumed not to change the background velocity. As a consequence, diffraction is obviously present.
Wave intensity around a carpet cloak for acoustic waves in moving fluids.
A Gaussian beam initially propagates along the positive x-direction. The wave is immersed in a fluid moving parallel to the aircraft wall (with speed 0.35cV) and thus suffers a dragging effect that deviates it from its original trajectory. (a) Wave impinging onto a flat wall. (b) Wave impinges onto a wall with a bump surrounded by a carpet cloak within which the background fluid flows with the same velocity as outside the cloak. The wave outside the cloak is significantly distorted compared to the flat-wall case. (c) As in (b), but now the background fluid flows with a modified velocity calculated with the analogue transformation method. Outside the cloak, the wave recovers the form it had in the flat-wall case: the bump is perfectly cloaked. See Supplementary Information for more details.
In addition, STA prescribes for the case of three-dimensional transformations that sound speed and density must be increased or decreased simultaneously at each point, while the opposite behavior is obtained with the analogue approach (see Supplementary Information). This latter requirement is more in line with current state-of-the-art acoustic metafluids. These are typically built by putting a lattice of rigid objects in air and (unlike in natural fluids) an increase of density corresponds to a decrease of the speed of sound and vice versa23,24. Thus, we expect the construction of metamaterial devices designed with the new method to be easier.
Finally, note that the equations used in the text do not contain any approximation apart from the ones necessary to obtain equations (1) and (2) from basic fluid dynamics principles. Therefore, the analogue transformations method works both in the wave and eikonal regimes. On the other hand, as mentioned above, in some cases the acoustic parameters transform differently depending on whether one works with equation (1) or equation (2). However, both values are correct as long as the assumptions used to obtain the corresponding wave equation are valid.
Discussion
Given that we have described our method in abstract terms, it is natural to ask how general this approach is. The answer depends on our ability to construct an analogue theory that mirrors the properties of the relevant equations. Two specific examples in this respect are the following. First, phonons in Bose-Einstein condensates provide an analogue model of a massless scalar field28,29. Second, graphene provides an analogue model of relativistic electrons30, so this method could become a powerful tool to control electronic propagation and confinement in a graphene sheet. In practice, the local manipulability of the propagating (meta)media will be crucial. In the case of graphene, the conductivity could be controlled by introducing curvature31 or by varying the chemical potential32. More in general, the method presented here can be applied to any system which provides an analogue model of a relativistic field, i.e. scalar fields, electromagnetic fields, Dirac and Weyl spinorial fields and even spin-2 (gravitational) fields (for a non-exhaustive list of examples of laboratory systems where a relativistic analogue has already been developed, see19). In all these examples, the problem of the non-form-invariance of the equations describing a given system can be circumvented through the construction of an analogue theory. All in all, our results indicate that the idea underneath transformation optics has an even far richer scope than initially foreseen.
Methods
Numerical simulations have been performed with the commercially available COMSOL Multiphysics simulation software, which is based on the finite element method. For full-wave simulations, the velocity potential wave equation has been numerically solved using COMSOL's acoustic module.
The trajectories followed by acoustic rays in the geometrical approximation have been calculated by solving Hamilton's equations:


In our case, the Hamiltonian equals the angular frequency, which can be obtained from the dispersion relation associated to the velocity potential wave equation under the assumption of plane-wave solutions of the form φ = φ0ej(k·r−ωt). Thus, it can be shown that the sought Hamiltonian is (k = |k|)

References
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).
Schurig, D. et al. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 314, 977–980 (2006).
Shalaev, V. M. Transforming Light. Science 322, 384–386 (2008).
Greenleaf, A., Kurylev, Y., Lassas, M. & Uhlmann, G. Invisibility and inverse problems. B. Am. Math. Soc. 46, 55–97 (2009).
Genov, D. A., Zhang, S. & Zhang, X. Mimicking celestial mechanics in metamaterials. Nat. Phys. 5, 687–692 (2009).
Chen, H., Chan, C. T. & Sheng, P. Transformation optics and metamaterials. Nat. Mater. 9, 387–396 (2010).
Leonhardt, U. & Philbin, T. Geometry and light. The science of invisibility (Dover Publications, 2010).
Pendry, J. B., Aubry, A., Smith, D. R. & Maier, S. A. Transformation Optics and Subwavelength Control of Light. Science 337, 549 (2012).
Post, E. G. Formal Structure of Electromagnetics: General Covariance and Electromagnetics (Interscience Publishers, New York, 1962).
Cummer, S. A. & Schurig, D. One path to acoustic cloaking. New J. Phys. 9, 45 (2007).
Chen, H. & Chan, C. T. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 91, 183518 (2007).
Norris, A. N. Acoustic metafluids. J. Acoust. Soc. Am. 125, 839 (2009).
Chen, H. & Chan, C. T. Acoustic cloaking and transformation acoustics. J. Phys. D: Appl. Phys. 43, 113001 (2010).
Zhang, S., Genov, D. A., Sun, C. & Zhang, X. Cloaking of Matter Waves. Phys. Rev. Lett. 100, 123002 (2008).
McCall, M. W., Favaro, A., Kinsler, P. & Boardman, A. A spacetime cloak, or a history editor. J. Opt. 13, 024003 (2011).
Fridman, M., Farsi, A., Okawachi, Y. & Gaeta, A. L. Demonstration of temporal cloaking. Nature 481, 62–65 (2012).
Cummer, S. A. & Thompson, R. T. Frequency conversion by exploiting time in transformation optics. J. Opt. 13, 024007 (2011).
Barceló, C., Liberati, S. & Visser, M. Analogue Gravity. Living Rev. Relativity 14, 3 (2011).
Visser, M. Acoustic black holes: Horizons, ergospheres and Hawking radiation. Class. Quant. Grav. 15, 1767 (1998).
Barceló, C. & Jannes, G. A Real Lorentz-FitzGerald contraction. Found. Phys. 38, 191 (2008).
Bergmann, P. G. The Wave Equation in a Medium with a Variable Index of Refraction. J. Acoust. Soc. Am. 17, 329 (1946).
Torrent, D., Håkansson, A., Cervera, F. & Sánchez-Dehesa, J. Homogenization of two-dimensional clusters of rigid rods in air. Phys. Rev. Lett. 96, 204302 (2006).
Torrent, D. & Sánchez-Dehesa, J. Effective parameters of clusters of cylinders embedded in a nonviscous fluid or gas. Phys. Rev. B 74, 224305 (2006).
Unruh, W. G. Experimental black hole evaporation? Phys. Rev. Lett. 46, 1351 (1981).
Li, J. & Pendry, J. B. Hiding under the Carpet: A New Strategy for Cloaking. Phys. Rev. Lett. 101, 203901 (2008).
Popa, B. I., Zigoneanu, L. & Cummer, S. A. Experimental acoustic ground cloak in air. Phys. Rev. Lett. 106, 253901 (2011).
Garay, L. J., Anglin, J. R., Cirac, J. I. & Zoller, P. Black holes in Bose-Einstein condensates. Phys. Rev. Lett. 85, 4643 (2000).
Lahav, O., Itah, A., Blumkin, A., Gordon, C. & Steinhauer, J. Realization of a sonic black hole analogue in a Bose-Einstein condensate. Phys. Rev. Lett. 105, 240401 (2010).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109 (2009).
Cortijo, A. & Vozmediano, M. A. H. Electronic properties of curved graphene sheets. Europhys. Lett. 77, 47002 (2007).
Vakil, A. & Engheta, N. Transformation optics using graphene. Science 332, 1291 (2011).
Acknowledgements
This work was developed under the framework of the ARIADNA contract 4000104572/11/NL/KML of the European Space Agency. A. M. and J. S.-D. also acknowledge support from Consolider EMET project (CSD2008-00066), A. M. from project TEC2011-28664-C02-02, J.S.-D. from US Office of Naval Research and C. B. and G. J. from the project FIS2008-06078-C03-01. We thank Reme Miralles for her help with Fig. 2.
Author information
Authors and Affiliations
Contributions
S.C. proposed to explore the combination of transformation acoustics and analogue gravity. C.G.-M. devised the final method, developed the main theory and performed the simulations. C.B., G.J. and S.C. contributed in several important theoretical aspects of this work. C.G.-M. and J.S.-D. analyzed the implementation advantages of the proposed method. A.M. assisted with the simulations. All authors participated in the manuscript preparation and discussed the results. S.C. and A.M. coordinated the work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
García-Meca, C., Carloni, S., Barceló, C. et al. Analogue Transformations in Physics and their Application to Acoustics. Sci Rep 3, 2009 (2013). https://doi.org/10.1038/srep02009
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02009
This article is cited by
-
Design of metacontinua in the aeroacoustic spacetime
Scientific Reports (2020)
-
Design method for an acoustic cloak in flows by topology optimization
Acta Mechanica Sinica (2019)
-
Effect of compressibility and non-uniformity in flow on the scattering pattern of acoustic cloak
Scientific Reports (2017)
-
Optical Surface Transformation: Changing the optical surface by homogeneous optic-null medium at will
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


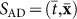 using the transformation f: SAC → SAD that encodes the desired distortion. One can apply any transformation one likes since the relativistic equations always maintain their form. This yields a new functional form for the geometric coefficients
using the transformation f: SAC → SAD that encodes the desired distortion. One can apply any transformation one likes since the relativistic equations always maintain their form. This yields a new functional form for the geometric coefficients 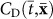 . Then, rename the new coordinates
. Then, rename the new coordinates 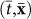 to (t, x).
to (t, x).


