Abstract
In this work, we present a theoretical method to determine the line tension of nanodroplets on homogeneous substrates via decomposing the grand free energy into volume, interface and line contributions. With the obtained line tension, we check the viability of Young equation and find that the chemical potential dependence (or equivalently, droplet curvature dependence) of the interface tensions is crucial for the viability of modified Young equation at the nanometer scale. In particular, the linear relationship between the cosine of contact angle and the curvature of the contact line, which is often used to determine the line tension, is found to be incorrect at the nanometer scale.
Similar content being viewed by others
Introduction
Understanding on the line tension becomes particularly important because of its relevance to a number of applications, such as soft lithography1,2, micro- and nanofluidics3 and nucleation4,5. Nevertheless, the contact line tension, well defined as the excess free energy of a solid-liquid-vapor system per unit length of a contact line, remains controversial6,7,8 largely because the direct measurement of the line tension of droplets has not been possible. There is no agreement among researchers with respect to both the sign and the magnitude of the line tension. Experimental values in the literature range from 10−11 to 10−5 J/m and both positive and negative signs for the line tension were reported7,9,10. In theoretical studies, however, most of the estimates for the magnitude of the line tension range from10−12 to 10−10 J/m, near the lower limit of the experimental values5,7,11. Recently, even the existence of the line tension is under debate in the literature12.
The uncertainty of the contact line tension also leads to controversy for the viability of modified Young equation12,13,14, which relate the apparent contact angle θ for a drop/bubble atop of solid substrates and the line tension τ as

with γij the interface tensions for different interfaces. Even though the modified Young equation is extensively applied, whether it can hold or not at the nanometer scale has been questioned in recent years, partly because the original Young equation is virtually impossible to prove experimentally14. For example, Ward and Wu12 suggested that it is not the line tension but the adsorption effect that can explain the dependence of the contact angle on the contact line curvature.
In this work, we present a method to determine the line tension accurately via decomposing the grand free energy of a nanodroplet on a homogeneous substrate into volume, interface and line contributions. By using the metastable vapor state at the same thermodynamic conditions as the initial state, the free energy cost for the formation of the nanodroplets can be written as

with Vl the volume of the droplet, Aij the area for different interfaces, L the length of the contact line, ωi the bulk free energy density of liquid or vapor. In this work, nanodroplets are modeled as critical nuclei for vapor-to-liquid phase transition on solid substrates to eliminate the non-equilibrium effect which cannot be neglected for microscopic droplets15. We chose lattice gas model to describe the systems and the normal lattice density functional theory (LDFT)16,17 was used here to determine the stable or metastable states. While for the unstable critical nuclei (nanodroplets), the constrained LDFT method18,19 was applied here to stabilize the nuclei and determine the corresponding energy barrier, namely ΔΩ in equation (2). The physical basis of the constrained LDFT and calculation details can be found in ref.19. Besides, the volume and interface contributions to the grand free energy can also be calculated separately through different systems using either normal LDFT or constrained LDFT (see below) and thus the line tension can be accurately determined through equation (2). With the accurately determined line tension, we also checked the viability of modified Young equation at the nanometer scale.
Results
Before we present our simulation results, we briefly show that the system with critical nuclei produced from our constrained LDFT is in thermodynamic equilibrium with the bulk phase (surrounding supersaturated vapor), therefore eliminating the evaporation effect of nanodroplets15. The thermodynamic equilibrium is also a prerequisite of the applicability of the free energy decomposition mentioned above: different thermodynamic phases coexist in equilibrium. Using homogeneous nucleation as an example, we obtained critical nuclei from constrained LDFT and then determined the Gibbs dividing interface (see Fig. 1a). The corresponding local density (ρ) and chemical potential (μ) distributions are shown in Fig. 1b and Fig. 1c, respectively. The radial profiles of μ in Fig. 1c indicate that thermodynamic equilibrium is achieved between the nanodroplets (critical nuclei) and the surrounding vapor. Therefore, nanodroplets studied in this work are modeled as critical nuclei at the given temperature and chemical potential, with advantages of bias free and free of non-equilibrium effect. Moreover, Fig. 1b indicates that at the same chemical potential, the local density of the vapor (liquid) region for a system with a critical nucleus is identical with that of the bulk vapor (liquid) phase13. This same density profile makes it possible to calculate separately the volume, interface and line contributions of the grand free energy from different systems, as shown below.
Thermodynamic equilibrium of critical nuclei with surrounding supersaturated vapor.
(a) Critical nucleus for homogeneous nucleation and the fitted Gibbs dividing interface at μ = −2.975. (b, c) Radial distribution of local chemical potential μ and density ρ for the critical nuclei of homogeneous nucleation. The small pictures on the right and left sides show the corresponding results in bulk vapor and liquid phases at the same chemical potential.
The volume terms of the grand free energy, ωland ωv, are first determined in bulk systems with normal LDFT calculations, separately (see Fig. 2a for schematic illustration). Fig. 2b shows the difference of the free energy density between liquid and vapor bulk phases obtained from ωl − ωv = (Ωl − Ωv)/V, with Ωl and Ωv the grand free energy for bulk liquid and vapor phases, respectively. The coexistence chemical potential for vapor-liquid phase transition was found to μc = −3.018,19, at which ωl = ωv(see Fig. 2b).
The determination of ωl − ωv and γvs − γlswith normal LDFT.
(a, c) Illustration of the systems used to determine (a) ωl − ωv and (c) γvs − γls with normal LDFT. (b) bulk free energy density difference between liquid and vapor phase, determined with ωl − ωv = (Ωl − Ωv)/V. (d) The interface tension difference between vapor-solid and liquid-solid interfaces (γvs − γls) determined at different εsf and μ.
By using normal LDFT, the value of γvs − γls in equation (2) was then calculated from the difference of interface tensions between planar vapor-solid and liquid-solid interfaces (see Fig. 2c). We first simulated adsorption and desorption isotherms for fluids in a simulation box with a planar inert substrate at (100) surface and obtained the free energy of the whole system (i.e. Ωls and Ωvs) at different chemical potentials. The values of γlsand γvs at different fluid-solid interactions were then determined from the excess grand free energy with respect to the corresponding bulk phases, namely γls = (Ωls − Vlωl)/Als and γvs = (Ωvs − Vvωv)/Avs. Finally, the variation of γvs − γls as a function of the chemical potential is given in Fig. 2d.
For the vapor-liquid surface tension, we first computed the surface tension for the planar vapor-liquid surface, which is in equilibrium state only at the coexistence chemical potential of μc = −3.0. With normal LDFT calculations, the free energy difference between this system and the bulk vapor phase at the same chemical potential ΔΩ was determined and thus the surface tension for the planar vapor-liquid interface is calculated from γlv = (ΔΩ− Vl(ωl − ωv))/Alv, with ωl − ωv determined before (see Fig. 2b). In lattice model, the surface tension is weakly direction dependent25. The small difference between two different orientations is caused by the lattice effect and would become negligible at the high temperature we adopted. The surface tension for the interface at (100) plane is γlv(100) = 0.1389 at T = 1.2 (Tc ~ 1.5).
Using the constrained LDFT, we then computed the vapor-liquid surface tension for nanodroplets (critical nuclei) in the absence of substrates (see Fig. 3a for schematic illustration). As the first step, we simulated critical nuclei at various chemical potentials and determined the corresponding nucleation barriers ΔΩ. Then the surface tension at a given chemical potential is determined by γlv = (ΔΩ − Vl(ωl − ωv))/Alv. Our simulation results show that at a constant temperature, there exists a one-to-one correspondence between the chemical potential (μ) and the radius of a critical nucleus (R) for the bulk vapor-to-liquid phase transition (see Fig. 3b), under the boundary condition of R- > ∞ at μc = −3.0. Therefore, chemical potential dependence of surface tension is equivalent to the droplet curvature dependence, at least in the cases of critical nuclei. For growing or evaporating droplets, which are in a nonequilibrium state, the one-to-one correspondence between μ and R breaks down. However, Moody and Attard20 show that the local supersaturation (namely local chemical potential) above a growing droplet can be determined by the Young-Laplace equation. It implies that the chemical potential, both global and local, depends on the droplet curvature.
The determination of critical nuclei for both homogenous and heterogeneous nucleation with constrained LDFT.
(a–c) Homogeneous nucleation to determine the vapor-liquid surface tension γlv with constrained LDFT: (a) illustration of the systems used; (b) The relationship between the chemical potential μ and radius of critical nucleus R; (c) γlv(R) versus R and γlv versus 1/R (inset). The full triangles in (c) represent R obtained from the equimolar method and open triangles from the method by Schrader et al13. (d–f) Heterogeneous nucleation on planar substrates: (d) illustration of the systems used and critical nucleus at (e) εsf = 0.30 and (f) 0.55. The red line in (e,f) shows the fitted Gibbs dividing interface and the blue line indicates the fluid-solid interface at the mid-point between solid substrate and the fluid particles closest.
With the one-to-one correspondence between μ and R, the surface tension γlv is given in Fig. 3c as a function of R. It is found that the relative deviation between γlv(R) and  increases with decreasing R, and reaches ~8% for R = 4. Note that in this work we used two methods to define the position of the vapor–liquid interface. One is the Gibbs dividing surface for the vapor-liquid interfaces with the fluid density equal to 0.519, from which we could fit the interface using a spherical hypothesis and obtain the radius of a droplet. The other is a method used by Schrader et al.13, in which the droplet radius R is calculated from the volume of a liquid droplet with Vl = 4/3πR3 and Vl = V(ρ − ρv)/(ρl − ρv). As shown in Fig. 3c, the two methods give the same results. The inset of Fig. 3c also shows the corresponding fitting results of γlv(R) from the equation originated from modified classical nucleation theory, γlv(R) = γlv(∞)(1 − 2δ/R + σ/R2)21,22, giving γlv(∞) = 0.1405, the Tolman length δ = −0.009 and the offset parameter σ = −1.3106. The small value of δ is in agreement with the fact that for the lattice gas the Tolman length is zero at the coexistence23,24. The observation of the value of
increases with decreasing R, and reaches ~8% for R = 4. Note that in this work we used two methods to define the position of the vapor–liquid interface. One is the Gibbs dividing surface for the vapor-liquid interfaces with the fluid density equal to 0.519, from which we could fit the interface using a spherical hypothesis and obtain the radius of a droplet. The other is a method used by Schrader et al.13, in which the droplet radius R is calculated from the volume of a liquid droplet with Vl = 4/3πR3 and Vl = V(ρ − ρv)/(ρl − ρv). As shown in Fig. 3c, the two methods give the same results. The inset of Fig. 3c also shows the corresponding fitting results of γlv(R) from the equation originated from modified classical nucleation theory, γlv(R) = γlv(∞)(1 − 2δ/R + σ/R2)21,22, giving γlv(∞) = 0.1405, the Tolman length δ = −0.009 and the offset parameter σ = −1.3106. The small value of δ is in agreement with the fact that for the lattice gas the Tolman length is zero at the coexistence23,24. The observation of the value of  close to the value of γlv(100) demonstrates that the temperature we chosen is sufficiently high to minimize the anisotropy effect of the lattice model25.
close to the value of γlv(100) demonstrates that the temperature we chosen is sufficiently high to minimize the anisotropy effect of the lattice model25.
Finally, using constrained LDFT we calculated the free energy costs for the formation of various critical nuclei on planar substrates (the vapor-to-liquid heterogeneous nucleation),  and determined the corresponding radius of the critical nuclei (see Fig. 3e,3f for typical snapshots of critical nuclei and the fitted vapor-liquid interfaces). It is found that droplet radii from heterogeneous nucleation are almost the same for those from homogenous nucleation at the same chemical potential and temperature (see Fig. 1a, 4e and 4f).
and determined the corresponding radius of the critical nuclei (see Fig. 3e,3f for typical snapshots of critical nuclei and the fitted vapor-liquid interfaces). It is found that droplet radii from heterogeneous nucleation are almost the same for those from homogenous nucleation at the same chemical potential and temperature (see Fig. 1a, 4e and 4f).
With the obtained results for the nucleation barrier for nanodroplet formations and the volume and interface contributions to the grand free energy (see Fig. 2 and Fig. 3), we could determine the line tension from equation (2). Fig. 4a–e show the obtained line energy τL as a function of the droplet circumference L = 2πr for different values of εsf. Good linear relationships are observed from the figures, indicating that the line tension is chemical potential independent, namely the line tension can be treated as a constant at a fixed temperature and fluid-solid interaction. The line tension determined from the slope of the linear regression line is shown in Fig. 4f as a function of the fluid-solid interaction. The figure shows that the line tension is always negative26 and reaches a minimal value at εsf = 0.50. Taking σ = 0.37 nm and εff = 7.9226 × 10−21 J27, the values of the line tension obtained in this work is about 10−11 J/m. The magnitude of those results is consistent with some theoretical predictions and experimental results28,29.
Discussion
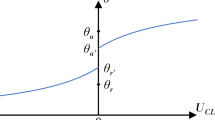
Above we showed that all quantities in modified Young equation, namely equation (1), including the three interface tensions and the line tension and the apparent contact angle, can be accurately determined from our calculations. Therefore, we can check the viability of Young equation at the nanometer scale. In Fig. 5a we give the contact angle calculated from modified Young equation and those direct ‘measured’ from our calculations (see, e.g., Fig. 3e). Fig. 5a shows that if and only if the chemical potential dependence of interface tension (see Fig. 2 and Fig. 3) is correctly taken into account, the contact angles of nanodroplets from modified Young equation (equation (1)) agree with those from direct ‘measurement’. If the chemical potential dependence of the three interface tensions are ignored (e.g., as in Fig. 5a, we set the three interface tensions constant to those at μc = −3.0), contact angles from modified Young equation would substantially deviate from the measured values from constrained LDFT and the deviation increases with the decrease of the radius of contact lines, r. Hence, the chemical potential dependence of interface tensions can not be ignored for the validness of Young equation at the nanometer scale. This also implies that the linear relationship between the cosine of a apparent contact angle and the curvature of a contact line, which was often used in experiments and simulations to determine the line tension9,11, is no longer valid at the nanometer scale.
The viability of Young equation and adsorption effect.
(a) Comparison of cosθ measured from our constrained LDFT calculation (symbols) and those calculated from the modified Young equation with (solid line) and without (dash line) considering the chemical potential dependence of the three interface tensions. (b) Obtained line tension from the linear regression of cosθ ~1/r. (c) The cosine of Young contact angle determined by original Young equation versus droplet curvature 1/R. (d) The difference in Young contact angle relative to the value θY at 1/R = 0 (i.e. μc = −3.00).
To confirm this point, we determined the line tension alternatively by using the linear regression line of cosθ ~1/r and the “apparent” line tensions obtained are shown in Fig. 5b. The “apparent” line tension is about one order of magnitude smaller than the line tension computed from the method of decomposing the grand free energy (Fig. 4). For most partial wetting situations, e.g., εsf = 0.40 or larger, the cosθ increases with increasing 1/r, indicating a negative “apparent” line tension. But for the case of εsf = 0.30, cosθ decreases with increasing 1/r, we therefore obtained a positive “apparent” line tension. The significant deviation of the line tensions from those for the method with free energy decomposition (see Fig. 5a,b) indicate that the linear relationship between the cosine of local contact angle and local curvature of contact line is incorrect at the nanometer scale.
The deviation from the linear relationship between cosθ and 1/r can be explained from the chemical potential dependence of the three interface tensions (Fig. 2d and Fig. 3c), namely the interface tension effect. As to the effect of vapor-liquid surface tension, the increase of the chemical potential, which induces smaller droplets and a smaller γlv (see Fig. 3c), tends to increase (decrease) the contact angle at negative (positive) γvs − γls. As to the effect of fluid-solid interface tensions, however, the increase of the chemical potential results in the decrease of γvs − γls (see Fig. 2d), giving rise in the increase of the contact angle. This fluid-solid interface effect in fact is an adsorption effect12,30: the fluid-solid interface tension depends on the fluid adsorption on the substrates, leading to different Young contact angles at different chemical potentials. The Young contact angle θY without considering the line tension effects calculated by the original Young equation,  , is given in Fig. 5c as a function of droplet curvature (also chemical potential), indicating that the interface tension effect make the contact angle larger. The deviation of Young contact angle θY(R) relative to θY(∞) (see Fig. 5d) also indicates the more significant influence of the chemical potential for smaller droplets.
, is given in Fig. 5c as a function of droplet curvature (also chemical potential), indicating that the interface tension effect make the contact angle larger. The deviation of Young contact angle θY(R) relative to θY(∞) (see Fig. 5d) also indicates the more significant influence of the chemical potential for smaller droplets.
The εsf dependence of cosθY(∞)− cosθY(R) in Fig. 5d also shows that the effect of chemical potential alone can not explain the dependence of the contact angle on the droplet size (also chemical potential). In other words, the line tension has to be considered. The apparent contact angle is in fact a result of competition between the chemical potential dependence of interface tension effect and the line tension effect: the interface tension effect increases the contact angle and the negative line tensions tend to decrease the contact angle. For example, for the cases of εsf > 0.30, the small values of cosθY(∞)− cosθY(R) indicate a weak interface tension effect (see Fig. 5d), while the line tension effect is strong (see Fig. 4f). Thus, the contact angle is lower for smaller droplets, exhibiting a negative “apparent” line tension, because the line tension effect overweighs the interface tension effect (see Fig.5b). But, in other cases (e.g., εsf = 0.30 or smaller) where the line tension effect becomes weaker than the interface tension effect, the contact angle may becomes larger for smaller droplets. That is why we got positive “apparent” line tension at εsf = 0.30 (see Fig. 5b). More importantly, it is the competitive mechanism that makes the linear relationship in modified Young equation no longer valid.
In summary, we presented a method to determine accurately the line tension for nanodroplets on homogeneous substrates via decomposing the grand free energy. The obtained line tension is found to be chemical potential independent and always negative, reaching a minimal value at a moderate fluid-solid attraction. We also checked the viability of Young equation at the nanometer scale and found that if the dependence of interface tensions on the chemical potential is correctly taken into account, the contact angles of nanodroplets from our method agree with those from modified Young equation. However, we show that the extensively used linear relationship between the cosine of contact angles and the curvature of contact lines suggested by modified Young equation is in fact incorrect at the nanometer scale. Detailed inspection shows that the contact angle is in fact a result of competition between the effects of the chemical potential dependent interface tension and the effect of the chemical potential independent line tension.
Methods
For a grand canonical (μVT) ensemble, the grand potential Ω in lattice model is expressed as a function of the fluid density distribution via16,17,18,19

where the sums are restricted to fluid sites on the lattice and a is the vector from a site i to a nearest neighbor site. In equation (3), ρi is the mean density at site i,  represents external field and εff and εsf represent the strength of fluid-fluid interaction and that for fluid-solid interaction, respectively. In order to obtain the information of transition states (critical nucleus), a volume constraint of
represents external field and εff and εsf represent the strength of fluid-fluid interaction and that for fluid-solid interaction, respectively. In order to obtain the information of transition states (critical nucleus), a volume constraint of  with NL0 the target number of liquid sites (the given volume of the nucleus) and NL its actual value in our calculations was added in equation (3) and thus the constrained grand potential
with NL0 the target number of liquid sites (the given volume of the nucleus) and NL its actual value in our calculations was added in equation (3) and thus the constrained grand potential  can be written as
can be written as  18,19. With
18,19. With  and
and  , we get the density profile via18,19
, we get the density profile via18,19

in which χi is defined as  . The local density
. The local density  and Lagrange multiplier
and Lagrange multiplier  were solved iteratively in our calculation19.
were solved iteratively in our calculation19.
References
Peters, R. D., Yang, X. M., Kim, T. K. & Nealey, F. Wetting behavior of block copolymers on self-assembled films of alkylchlorosiloxanes: effect of grafting density. Lanmguir 16, 9620–9626 (2000).
Lopes, W. A. & Jaeger, H. M. Hierarchical self-assembly of metal nanostructures on diblock copolymer scaffolds. Nature 414, 735 (2001).
Whitesides, G. M. & Stroock, A. D. Flexible methods for microfluidics. Phys. Today 54, 42 (2001).
Auer, S. & Frenkel, D. Line tension controls wall-induced crystal nucleation in hard-sphere colloids. Phys. Rev. Lett. 91, 015703 (2003).
Winter, D., Virnau, P. & Binder, K. Monte carlo test of the classical theory for heterogeneous nucleation barriers. Phys. Rev. Lett. 103, 225703 (2009).
Drelich, J. The significance and magnitude of the line tension in three-phase (solid-liquid-fluid) systems. Colloids Surf. A 116, 43–54 (1996).
Amirfazli, A. & Neumann, A. W. Status of the three-phase line tension. Adv. Colloid Interface Sci. 110, 121–141 (2004).
Schimmele, L., Napiórkowski, M. & Dietrichl, S. Conceptual aspects of line tensions. J. Chem. Phys. 127, 164715 (2007).
Stöckelhuber, K. W., Radoev, B. & Schulze, H. J. Some new observations on line tension of microscopic droplets. Colloids Surf. A 156, 323–333 (1999).
Checco, A. & Guenoun, P. Nonlinear dependence of the contact angle of nanodroplets on contact line curvature. Phys. Rev. Lett. 91, 186101 (2003).
Weijs, J. H., Marchand, A., Andreotii, B., Lohse, D. & Snoeijer, J. H. Origin of line tension for a Lennard-Jones nanodroplet. Phys. Fluids 23, 022001 (2011).
Ward, C. A. & Wu, J. Effect of contact line curvature on solid-fluid surface tensions without line tension. Phys. Rev. Lett. 100, 256103 (2008).
Schrader, M., Virnau, P. & Binder, K. Simulation of vapor-liquid coexistence in finite volumes: A method to compute the surface free energy of droplets. Phys. Rev. E 79, 061104–12 (2009).
Méndez-Vilas, A., Jódar-Reyes, A. B. & González-Martín, M. L. Ultrasmall liquid droplets on solid surfaces: production, imaging and relevance for current wetting research. Small 5, 1366–1390 (2009).
Butt, H. J., Golovko, D. S. & Bonaccurso, E. On the derivation of Young's equation for sessile drops: nonequilibrium effects due to evaporation. J. Phys. Chem. B 111, 5277–5283 (2007).
Kierlik, E., Monson, P. A., Rosinberg, M. L., Sarkisov, L. & Tarjus, G. Capillary condensation in disordered porous materials: hysteresis versus equilibrium behavior. Phys. Rev. Lett. 87, 055701 (2001).
Monson, P. A. Mean field kinetic theory for a lattice gas model of fluids confined in porous materials. J. Chem. Phys. 128, 084701 (2008).
Men, Y., Yan, Q., Jiang, G., Zhang, X. & Wang, W. Nucleation and hysteresis of vapor-liquid phase transitions in confined spaces: Effects of fluid-wall interaction. Phys. Rev. E 79, 051602 (2009).
Men, Y. & Zhang, X. Physical basis for constrained lattice density functional theory. J. Chem. Phys. 136, 124704 (2013).
Moody, P. M. & Attard, P. Curvature-dependent surface tension of a growing droplet. Phys. Rev. Lett. 91, 056104 (2003).
Dillmann, A. & Meier, G. E. A. A refined droplet approach to the problem of homogeneous nucleation from the vapor phase. J. Chem. Phys. 94, 3872 (1991).
Prestipino, S., Laio, A. & Tosatti, E. Systematic improvement of classical nucleation theory. Phys. Rev. Lett. 108, 225701 (2012).
Fisher, M. P. A. & Wortis, M. Curvature corrections to the surface tension of fluid drops: Landau theory and a sacling hypothesis. Phys. Rev. B 29, 6252–6260 (1984).
Anisimov, M. A. Divergence of Tolman's length for a droplet near the critical point. Phys. Rev. Lett. 98, 035702 (2007).
Saugey, A., Bocquet, L. & Barrat, J. L. Nucleation in hydrophobic cylindrical pores: a lattice model. J. Phys. Chem. B 109, 6520–6526 (2005).
Djikaev, Y. Histogram analysis as a method for determining the line tension of a three-phase contact region by Monte Carlo simulations. J. Chem. Phys. 123, 184704 (2005).
Jang, J., Schatz, G. C. & Ratner, M. A. Cappillary force in atomic force microscopy. J. Chem. Phys. 120, 1157–1160 (2004).
Pompe, T. & Herminghaus, S. Three-Phase Contact Line Energetics from Nanoscale Liquid Surface Topographies. Phys. Rev. Lett. 85, 1930–1933 (2000).
Errington, J. R. & Wilbert, D. W. Prewetting boundary tensions from monte Carlo simulation. Phys. Rev. Lett. 95, 226107 (2005).
Wang, C. et al. Critical dipole length for the wetting transition due to collective water-dipoles interactions. Sci. Rep. 2, 358 (2012).
Acknowledgements
This work is supported by National Natural Science Foundation of China (No. 21276007).
Author information
Authors and Affiliations
Contributions
Y.W.L. performed most of the numerical simulations. Y.W.L. and X.R.Z. carried out most the theoretical analysis. Y.W.L., J.J.W. and X.R.Z. contributed most of the ideas and wrote the paper. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Liu, Y., Wang, J. & Zhang, X. Accurate determination of the vapor-liquid-solid contact line tension and the viability of Young equation. Sci Rep 3, 2008 (2013). https://doi.org/10.1038/srep02008
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02008
This article is cited by
-
The Measurement of the Surface Energy of Solids by Sessile Drop Accelerometry
Microgravity Science and Technology (2018)
-
Adsorption energy as a metric for wettability at the nanoscale
Scientific Reports (2017)
-
The measurement of the surface energy of solids using a laboratory drop tower
npj Microgravity (2017)
-
Direct and accurate measurement of size dependent wetting behaviors for sessile water droplets
Scientific Reports (2015)
-
Anisotropy of Local Stress Tensor Leads to Line Tension
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.