Abstract
The investigation of regular and irregular patterns in nonlinear oscillators is an outstanding problem in physics and in all natural sciences. In general, regularity is understood as tantamount to periodicity. However, there is now a flurry of works proving the existence of “antiperiodicity”, an unfamiliar type of regularity. Here we report the experimental observation and numerical corroboration of antiperiodic oscillations. In contrast to the isolated solutions presently known, we report infinite hierarchies of antiperiodic waveforms that can be tuned continuously and that form wide spiral-shaped stability phases in the control parameter plane. The waveform complexity increases towards the focal point common to all spirals, a key hub interconnecting them all.
Similar content being viewed by others
Introduction
Since the realization that the century-old causal determinism of Boskovic and Laplace needed amendment due to the discovery of deterministic chaos, much effort was devoted during the last few decades to study the intricacies involving the interplay between regular and irregular oscillations produced by nonlinear systems. Traditionally, the emphasis has been in the study of the irregular chaotic oscillations. However, there is a whole class of remarkably regular oscillations that has so far escaped attention, namely antiperiodic oscillations. A quantity x(t) is said to evolve periodically when x(t + T) = x(t), where T is the period between repetitions. The less familiar class of antiperiodic oscillations that we study here obeys the relation x(t + T) = −x(t). Clearly, every antiperiodic pattern with antiperiod T is necessarily a periodic pattern with period 2T. Trivial examples of antiperiodicity are the trigonometric solutions of the harmonic oscillator  ,
,  , which satisfy the textbook identities sin(t + π) = −sin t, or cos(t + π) = −cos t, where π is the antiperiod and 2π is the period of the oscillations. The system of differential equations defining these trivial solutions is linear and too simple to be flexible enough for a number of applications: it generates only a single wave pattern and allows no changes to it other than rather uninteresting amplitude and/or frequency changes.
, which satisfy the textbook identities sin(t + π) = −sin t, or cos(t + π) = −cos t, where π is the antiperiod and 2π is the period of the oscillations. The system of differential equations defining these trivial solutions is linear and too simple to be flexible enough for a number of applications: it generates only a single wave pattern and allows no changes to it other than rather uninteresting amplitude and/or frequency changes.
Antiperiodicity is known in physics. For instance, Matsubara1,2 used this concept in the 1950s when calculating expectation values of physical observables of a quantum field theory at finite temperature, in the requirement that all bosonic and fermionic fields be periodic and antiperiodic, respectively. During the last two decades, antiperiodic problems were spotted and studied extensively in a number of fields. For example, for first-order ordinary differential equations, the classic criterion of Massera3 for periodicity was extended for antiperiodic boundary value problems by Y. Chen4,5. From antiperiodic boundary conditions, the interest shifted to the study of antiperiodic oscillations. Antiperiodicity was investigated for the heat equation6, for second-order Duffing-like7 and pendulum-like8 oscillators and several other systems9,10. Antiperiodic wavelets were discussed by T. Chen11. Antiperiodic solutions for higher-order nonlinear ordinary differential equations are known but for a few specific systems8,12. Smooth antiperiodic solutions are also known for quasi-linear partial differential equations13. These works contain references to additional papers dealing with antiperiodic solutions discovered for a plethora of nonlinear equations.
Results
So far, the knowledge accumulated about antiperiodic oscillations dealt substantially with providing existence proofs of isolated solutions for low-order equations under specific conditions, or for higher-order equations with somewhat contrived ad-hoc forms. Furthermore, the majority of flows studied involve driven (i.e. non-autonomous) systems. All this means that the study of antiperiodicity is still in its infancy and only a few sparse antiperiodic solutions are known for some particular equations.
Here, we report the experimental observation and numerical corroboration of apparently infinite sequences of such elusive antiperiodic oscillations in an autonomous electronic circuit (Fig. 1). Our key discovery is that the complexification of currents and voltages in the circuit occurs mediated by infinite families of self-sustained antiperiodic oscillations that can be tuned continuously as a function of the physical reactances involved. Nowadays, periodic waveforms are the rule in nonlinear systems while oscillators capable of supporting families of tunable antiperiodic waveforms with an unbounded number of peaks within an oscillation are completely unheard of. We detected tunable antiperiodicity while studying the complicated mechanisms underlying the progressive wave pattern complexification generated by the electronic circuit during period-doubling and period-adding cascades of bifurcations.
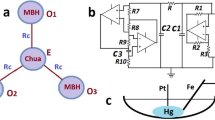
Schematic representation of the circuit used to measure the antiperiodic oscillations.
This circuit is governed by the differential equations C1dv1/dt = i1 − iR(v1), C2dv2/dt = −i1 − i2 − iG(v2), L1di1/dt = v2 − v1 − i1R1, L2 di2/dt = v2 − i2R2. The v-i characteristics of iR(v1) and iG(v2) are odd-symmetric functions given in the text.
As depicted in Fig. 1, our circuit involves two active elements, a nonlinear resistor R and a negative conductance G. It descends from a circuit considered by Chua and Lin14 and Stoupoulos et al.15. Our implementation contains a slight variation introduced to account for saturation effects of the real operational amplifier used in G. All phenomena observed with our modified circuit can be also observed in a circuit with ideal elements. For more details about the circuit, see Methods, below.
Figure 2 presents typical experimental signals obtained for the voltage v1(t) on the capacitor C1 as a function of the resistance R1 while maintaining all other parameters constant. From this figure we recognize the characteristic signature of antiperiodic oscillations, namely

where T/2 is the antiperiod and T is the period of the oscillation. From Fig. 2 it is easy to recognize that an antiperiodic function with antiperiod T is necessarily a periodic function with period 2T. Identical antiperiodicity is detected in measurements of v2, i1, or i2 (not shown). For all variables, we could follow the signal up to quite large number of spikes.
Experimental recordings of v1(t) (volts per ms) illustrating the successive complexification of antiperiodic wave patterns in the oscillator in Fig. 1, obtained when fixing L1 = 9.8 mH, L2 = 23.7 mH, R2 = 155 Ω and increasing R1 = 2143 Ω (3 peaks), 2175 Ω (5 peaks), 2224 Ω (7 peaks), 2288 Ω (9 peaks), 2298 Ω (11 peaks), 2313 Ω (13 peaks).
Note differences in time scales.
Figure 3 shows for v1, v2, i1, i2 the first few of an infinite sequence of antiperiodic oscillations. Such patterns were obtained from numerical integration when varying two parameters (given in the leftmost column) simultaneously. These oscillations have an odd number of spikes. Furthermore, the amplitude of the temporal evolutions of v2 (in the second column from the left) labeled s0, s2, is slightly smaller than the ones labeled s1 and s3. The same is true for i2 in the rightmost column.
Sequences of antiperiodic waveforms displaying the complexification of v1, v2, i1, i2 when two parameters are suitably tuned.
Voltages are measured in V, currents in mA, Ri in Ω and T in ms. The time scales, parameters and periods in the leftmost column apply to all panels in the same row. Labels si refer to the four parameter points marked by white dots in Fig. 4(a) and corresponds to turning points along the spiral phase shown in that figure.
To understand how antiperiodic patterns depend on R1 and R2 we performed an additional numerical experiment, studying the variation of the number of peaks systematically on a 2400 × 2400 = 5.76 × 106 rectangular grid of equally spaced parameter points. The circuit equations were integrated with a standard fourth-order Runge-Kutta algorithm with fixed time-step h = 10−6 s, starting computations always from a fixed initial condition v1 = 8 V, v2 = −5 V, i1 = −1 mA, i2 = 3 mA. The first 80 × 105 integration steps were discarded as transient. The chaotic/periodic/antiperiodic nature of solutions was determined and recorded in so-called isospike diagrams16: after the transient we integrated for an additional 80 × 105 time-steps and recorded extrema (maxima and minima) of a given variable of interest, up to 800 extrema, counting the number of peaks and checking whether for repetitions. Such high-resolution computations are numerically very demanding and, therefore, were performed on a SGI Altix cluster of 1536 high-performance processors running during a period of several weeks to compute many stability diagrams, three of them presented in Fig. 4.
(a) The spiral phase of self-sustained antiperiodic oscillations. Colors denote the number of peaks within one period of v2(t). Black denotes chaos, i.e. lack of numerically detectable repetitions. (b) Magnification of the box in (a) illustrating turning points with high odd-number of spikes (given by the numbers). Note the strong compression of the spiral phase embedded in the wide black background of chaos. (c) Magnification of the box in (b) showing the monotonous convergence towards the focal hub, the accumulation point approached when cycling the spiral anti-clockwisely, where periodic oscillations should have an infinite number of peaks within one period. Each individual panel displays the analysis of 2400 × 2400 = 5.76 × 106 parameter points. The resistances R1 and R2 are measured in Ω.
Figure 4 shows stability diagrams indicating how the number of peaks within one period of v2(t) self-organize in control space. As indicated by the colorbars, a palette of 17 colors is used to represent the number of peaks in one period of the oscillations. Patterns with more than 17 peaks are plotted by recycling the 17 basic colors modulo 17, namely assigning to them a color-index given by the remainder of the integer division of the number of peaks by 17. Multiples of 17 are given the index 17. Black represents “chaos” (i.e. lack of numerically detectable periodicity/antiperiodicity), white and gold colors mark constant (i.e. non-oscillatory) solutions, if any, having respectively non-zero or zero amplitudes of the variable under consideration.
The stability diagrams in Fig. 4 show that self-sustained non-chaotic (i.e. periodic or antiperiodic) oscillations manifest themselves by forming a main spiral phase converging to a focal hub and paving the control space with a multitude of colors. The colors indicate how the number of peaks increases and where exactly do they change along the spiral. From Fig. 4 one also sees that the number of peaks in v2(t) increases steadily by 2 after every turn towards the focal hub. Furthermore, while the period seems to accumulate to a definite limiting value, the number of peaks grows apparently without bound. From Fig. 4 it is also possible to recognize the presence of several additional secondary spirals sandwiched between every turn of the main spiral. From additional magnifications (not shown here) it is possible to recognize unambiguously an apparently unbounded hierarchy of such secondary spirals, that get thinner and thinner as one approaches more and more the focal hub. This hierarchical organization of spirals is similar to the one found recently in other physical oscillators17.
In Fig. 4(b) one sees that the edges, or legs, composing the main spiral display a certain angularity that becomes smoother and smoother near the hub, as it is clear from Fig. 4(c). This non-uniformity has to do, we believe, with the high-dimensionality of the parameter hypersurface defined by the flow: although motivated by experiments15, the parameters which were held fixed simply do not produce an optimal section of the hypersurface so as to reflect more regular and symmetric spirals. An optimization of all parameters involved would consume enormous amount of time and, therefore, was not attempted. It is important to mention, however, that in addition to the R2 × R1 control parameter plane, we also observed antiperiodic oscillations to induce similar spirals in other control planes, e.g. C1 × R1 and C1 × C2. Since resistances are easier to control experimentally than capacitances we preferred to focus here on the R2 × R1 plane. Antiperiodic patterns evolve continuously when parameters are suitably tuned along spirals. Furthermore, not only the period and the number of peaks but also the amplitude of the oscillations vary regularly when spiraling towards the hub.
Discussion
What is the mechanism responsible for the regular addition of peaks observed along the spiral? We find that such complexification occurs through continuous deformations of the wave patterns, analogously as described recently for a CO2 laser with feedback18 a system that, however, does not show antiperiodicity and has no spirals in its control space. For antiperiodicity to subsist indefinitely along the spirals as patterns get more and more complicated, it is necessary that wave pattern deformations occur in pairs, simultaneously. While odd-spiked antiperiodic oscillations were observed along the spiral, not all odd-spiked oscillations lead to antiperiodic oscillations. For instance, the wide one-spike phase seen on the top right corner of Fig. 4(a) is characterized by periodic oscillations (not by antiperiodicity). The same is true for the infinite peak-doubling cascades k × 2m issuing from a region of oscillations with k peaks.
Thus far our description was based on counting the number of peaks in the voltage v2(t). What happens when other variables are used to count peaks? Do the peaks of all four variables evolve in unison? Additional numerical work (not presented here) shows that, although each variable produces parameter sub-divisions, phases, having their own idiosyncrasies, the picture described for v2(t) remains basically unchanged. Changes in the number of peaks may, or not, require a complete turn along the spiral. Furthermore, the precise location where changes occur may vary slightly, depending on the variable considered. An attempt to uncover the systematics behind all possible changes would only make sense after solving the aforementioned parameter optimization problem. This optimization, of course, is not needed for our present purpose of reporting the discovery of infinite families of the elusive antiperiodic oscillations.
In what sort of systems can one expect to find antiperiodicity? The dissipative flow governing our circuit can be written compactly as dx/dt = f(x), where x = (v1, v2, i1, i2) and the four components of f(x) are given explicitly in the caption of Fig. 1. From these components we recognize that the flow is odd-symmetric, namely that f(−x) = −f(x). We have also observed similar antiperiodicity scenarios in another circuit, containing two diodes as a nonlinear resistance and in a few flows constructed ad-hoc to display this symmetry. This makes us believe that antiperiodicity should be present for a whole class of nonlinear oscillators having such symmetry. Thus, odd-symmetry of the flow seems to be a key ingredient for the onset of antiperiodic oscillations although, as already mentioned, not every regular oscillation with odd-number of peaks in odd-symmetric flows is necessarily antiperiodic. General mathematical conditions concerning periodicity are known19. It would be nice to extend them to take antiperiodicity into account, something that does not seem to be completely trivial to do. For a given set of parameters, the ability to predict whether oscillations will be antiperiodic or periodic seems to be a quite hard mathematical problem that needs to be investigated.
In conclusion, we presented experimental and numerical evidence of the existence of infinite families of tunable antiperiodic oscillations in a real-life physical oscillator and extended what is presently known about such remarkably interesting oscillations. We believe tunable families of antiperiodic oscillations to be a generic feature for an extended class of oscillators. Antiperiodicity remains unexplored in nonlinear dynamics, is potentially interesting for applications and certainly deserves further study.
Methods
The active nonlinear elements R and G of the circuit in Fig. 1 are represented by the following odd symmetric v-i characteristics


Here, parameters are functions of the electronic components. So, Eb depends of the output voltage swing, Vsat, of the operational amplifier and of its input voltage, Vcc. The slopes Ga and Gb also depend on the non-zero forward voltage Vγ of the diodes, modeled here as an ideal diode and a battery. Unless otherwise stated, we follow previous works14,15 and fix L1 = 9.8 mH, L2 = 20.6 mH, C2 = 2C1 = 12 nF, E1p = 2.5 V, E2p = 11 V, Eb = 7.5 V, Ga = −0.7 mS, Gb = −0.5 mS, Gc = 3.35 mS, Gaa = −0.5 mS and Gbb = 0.5 mS.
Our circuit uses fast commuting 1N4148 diodes and TL084 operational amplifiers. The chip of the op-amps consists of four amplifiers such that the circuit could be easily mounted on a board and the nonlinear resistances R and G implemented using nearly identical operational amplifiers. The 1N4148 has a maximum recovery time of 4 ns and is usually employed in high-frequency applications. The input voltage of the operational amplifier was maintained constant along the experiment at Vcc = 15.0 ± 0.6 V. The other relevant parameters are Vγ = 0.65 ± 0.06 V and Vsat = 12.7 ± 0.9 V.
References
Matsubara, T. A new approach to quantum-statistical mechanics. Prog. Theor. Phys. 14, 351–378 (1955).
Coleman, P. Many Body Physics (Cambridge University Press, Cambridge, 2013).
Massera, J. L. The existence of periodic solutions of systems of differential equations. Duke J. Math. 17, 457–475 (1950).
Chen, Y. Q. On Massera's theorem for antiperiodic solution. Adv. Math. Sci. Appl. 9, 125–128 (1999).
Liu, B. An antiperiodic LaSalle oscillation theorem for a class of functional differential equations. J. Comp. Appl. Math. 223, 1081–1086 (2009).
Okochi, H. On the existence of anti-periodic solutions to a nonlinear evolution equation associated with odd subdifferential operators. J. Func. Anal. 91, 246–258 (1990).
Pu, H. & Yang, J. Existence of antiperiodic solutions with symmetry for some high-order ordinary differential equations. Bound. Val. Prob. 108 (2012) and references therein.
Chen, T., Liu, W. & Yang, C. Antiperiodic solutions for Liénard-type differential equation with p-Laplacian operator. Bound. Val. Prob. 194824 (2010) and references therein.
Girardi, M. & Matzeu, M. Existence of periodic solutions for some second order Hamiltonian systems. Rend. Lincei Mat. Appl. 18, 1–9 (2007).
Cheng, Y., Cong, F. & Hua, H. Antiperiodic solutions for nonlinear evolution equations. Adv. Diff. Eq. 165, (2012) and references therein.
Chen, H. L. Antiperiodic wavelets. J. Comp. Math. 14, 32–39 (1996).
Chen, T. & Liu, W. Antiperiodic solutions for higher-order Liénard type differential equation with p-Laplacian operator. Bull. Korean Math. Soc. 49, 455–563 (2012) and references therein.
Nakao, M. & Okochi, H. Antiperiodic solution for ttt − (σ(ux))x − uxxt = f(x, t). J. Math. Anal. Appl. 197, 796–809 (1996).
Chua, L. & Lin, G. N. Canonical realization of Chua's circuit family. IEEE Trans. Circ. Syst. 37, 885–902 (1990).
Stoupoulos, I. N., Miliou, A. N., Valaristos, A. P., Kyprianidis, I. M. & Anagnostopoulos, A. N. Crisis induced intermittency in a fourth-order autonomous electric circuit. Chaos Sol. Frac. 33, 1256–1262 (2007) and references therein.
Freire, J. G., Pöschel, T. & Gallas, J. A. C. Stern-Brocot trees in spiking and bursting of sigmoidal maps. Europhys. Lett. 100, 48002 (2012).
Vitolo, R., Glendinning, P. & Gallas, J. A. C. Global structure of periodicity hubs in Lyapunov phase diagrams of dissipative flows. Phys. Rev. E 84, 016216 (2011) and references therein.
Junges, L. & Gallas, J. A. C. Frequency and peak discontinuities observed in self-pulsations of a CO2 laser with feedback. Opt. Commun. 285, 4500–4506 (2012).
Gallas, J. A. C. On the origin of periodicity in dynamical systems. Physica A 283, 17–23 (2000).
Acknowledgements
J.G.F. was supported by FCT, Portugal through the Post-Doctoral grant SFRH/BPD/43608/2008. C.C. and A.C.M. acknowledge support from CSIC and PEDECIBA, Uruguay. J.A.C.G. thanks support from CNPq, Brazil. This work was supported by the Deutsche Forschungsgemeinschaft through the Cluster of Excellence Engineering of Advanced Materials. All bitmaps were computed at the CESUP-UFRGS clusters.
Author information
Authors and Affiliations
Contributions
C.C., A.M. and J.A.C.G. conceived and designed the experiments. C.C. performed the experiments. J.G.F. and J.A.C.G. performed the simulations. J.A.C.G. wrote the main manuscript. All authors discussed the results and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Freire, J., Cabeza, C., Marti, A. et al. Antiperiodic oscillations. Sci Rep 3, 1958 (2013). https://doi.org/10.1038/srep01958
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01958
This article is cited by
-
Emergence and Dynamics of Short Food Supply Chains
Networks and Spatial Economics (2021)
-
Periodicity hubs and spirals in an electrochemical oscillator
Journal of Solid State Electrochemistry (2015)
-
Discontinuous Spirals of Stable Periodic Oscillations
Scientific Reports (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.