Abstract
Connectivity is the key process that characterizes the structural and functional properties of social networks. However, the bursty activity of dyadic interactions may hinder the discrimination of inactive ties from large interevent times in active ones. We develop a principled method to detect tie de-activation and apply it to a large longitudinal, cross-sectional communication dataset (≈19 months, ≈20 million people). Contrary to the perception of ever-growing connectivity, we observe that individuals exhibit a finite communication capacity, which limits the number of ties they can maintain active in time. On average men display higher capacity than women and this capacity decreases for both genders over their lifespan. Separating communication capacity from activity reveals a diverse range of tie activation strategies, from stable to exploratory. This allows us to draw novel relationships between individual strategies for human interaction and the evolution of social networks at global scale.
Similar content being viewed by others
Introduction
Many different forces govern the evolution of social relationships making them far from random. In recent years, the understanding of what mechanisms control the dynamics of activating or deactivating social ties have uncovered forces ranging from geography to structural positions in the social network (e.g. preferential attachment, triadic closure), to homophily1. These finding are pervasive in empirical analyses across cultures, communication technologies and interaction environments2,3,4,5,6,7,8,9,10,11.
However, the incorrect assumption that time, attention and cognition are elastic resources has blurred the study of how individuals manage their social interactions over time12,13,14. Understanding such social strategies is not only of paramount importance to make progress in the characterization of human behavior, but also to improve our current description of social networks as evolutionary objects against the (aggregated) ever-growing or static pictures of the social structure.
Several reasons have hampered the observation of tie activation/deactivation dynamics in social networks at large scale: on the one hand, studies of diffusion based on datasets from pre-electronic eras have safely assumed that tie activation/deactivation is a much slower process than interactions within a tie and thus their dynamics might be safely neglected15,16,17. However, the current ability to communicate faster and further than ever accelerates tie dynamics in an unprecedented manner to the point that tie activation/deactivation may rival in time with processes like information spreading. On the other hand, available data about how ties form or decay were restricted to egocentric, small social networks and/or short periods of time which made it difficult to assess the universality of the results obtained and their extension to other situations5. Finally, although in some online social networks there are explicit rules for the establishment of social ties, in most cases activity is the only way to assess the existence of the tie18,19. Online social networks are plagued with this problem due to the cheap cost of maintaining “friends” which are in fact already deactivated relationships20. However, using activity as proxy for tie presence is a problem in most communication channels like mobile phone calls, emails, electronic social networks etc., since tie activity is very bursty21 and so far there is no clear method to discriminate those social ties that are already inactive from large-inter even times within active relationships42.
Results
Detection of tie activation/deactivation
To study the formation and decay of communication ties, we study the Call Detail Records (CDRs) from a single mobile phone operator over a period of 19 months. The data consists of the anonymized voice calls of about 20 million users that form 700 million communication ties. After filtering out all the incoming or outgoing calls that involve other operators, we only consider users that are active across the whole time period and retain only ties which are reciprocated. We refer to Methods Section and the Supplementary Information (SI) Section 7 for further details about the processing and the sampling of the datasets and for the comparison with another (smaller) database of Facebook communication through wall posts.
In most studies of communication networks a tie is assumed to be present if it shows any activity in the observation window22. However, since communication is bursty21, large inter-event times between interactions are likely and thus they might be unobserved or mistaken as tie decay or formation, specially if the observation window is short (see Fig. 1 and SI Section 1 ). For example, in our call database we find that the average time between tie communication events is 〈δtij〉 = 14 days (with σ = 18 days) and thus we might get spurious effects if the observation window is of the order of months, as repeated interactions may fall outside the observation window23.
Detection of tie activation/deactivation.
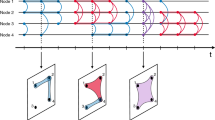
Schematic view of the time intervals considered in our database and the different situations of tie activation/deactivation and the interplay between the tie communication patterns and tie activation/deactivation for a given observation time window Ω of length T = 7 months (shadowed area). Each line refers to a different tie while each vertical segment indicates a communication event between i ↔ j and δtij is the inter-event time in the i ↔ j time series.
To overcome this we propose a different method to assess whether a tie has been activated/deactivated in the observation window Ω. The method is based on the observation of tie activity in a time window before/after Ω: if tie activity is observed in the 6 months before Ω then it is considered an old tie [cases (a) and (d) in Fig. 1]; on the other hand, if activity is observed in the 6 months after Ω we will assume that the tie persists [cases (b) and (d) in Fig. 1]. In any other case, we will consider that the tie is activated and/or deactivated in Ω [cases (a), (b) and (c) in Fig. 1]. Of course, it is possible that even if there is no communication before/after the observation window, the tie is still active after/before our database. This would require that the tie has an inter-event time δtij bigger than 7 months, i.e. case (e) in Fig. 1. However, in our database, only 3.5% of the links have such a long inter-event time which validates the accuracy of our definition of tie activation/deactivation. See Methods Section and SI Section 1 for details on our discrimination method.
Communication capacity and activity
The procedure described above allows us to determine the tie activation and deactivation events for each individual along the observation period of 7 months (see Fig. 2). With those events, we build her instantaneous communication capacity κi(t), defined as the number of active ties at any given instant t. In principle, κi(t) is very different from ki(t), the aggregated number of revealed ties up to time t, which is usually what is taken as a proxy for social connectivity23. Because of the bursty nature of interactions, ki(t) has a fictitious nontrivial time dynamics at the beginning of the observation period which is typically ignored in observations (see SI Section 1 for its implications). However, if we aggregate the number of activated (deactivated) ties up to time t, denoted by nα,i(t) [nω,i(t)], we get that at the end of Ω we have ki(T) = κi(0) + nα,i(T). Thus ki(T) is a combination of the communication capacity and communication activity in Ω. In our database we find a large heterogeneity in nα,i(T) and nω,i(T) [see Fig. 3a]: while on average people activate/deactivate about 8 (reciprocated) ties in a period of 7 months, 20% of users in our database activate/deactivate more than 15 ties in that period. Note that on average nα,i(T) and nω,i(T) almost equals ki(T)/2, (see Fig. 3a), which suggests that a large fraction of the revealed aggregated social connectivity ki(T) is given by newly activated or deactivated connections; similar ratio of activation/deactivation is found in the Facebook database (see SI Section 7). Thus, ki(T) usually overestimates the instantaneous human communication capacity of maintaining active social ties.
Communication capacity and evolution of activity.
Panel (A) shows the communication events of a given individual in our database with all her neighbors in the observation window Ω.For each tie id, a vertical line represents a call with the corresponding neighbor. Grey horizontal rectangles are drawn from the first to the last observed communication event in each tie, considering also events before and after Ω. Panel (B) shows vertical up/down arrows for each tie activation/deactivation events detected within Ω. Using those events, panel (C) shows the aggregated number of active ties as a function of time κi(0) + nα,i(t) and the aggregated number of deactivated ties nω,i. Dashed line is the apparent growth in the social connectivity ki(t) obtained by the cumulative number of observed activity in ties up to some time, while red line is the number of active connections at a given instant κi(t).
Characterization of communication capacity and activity.
(A) Probability distribution function (pdf) of the aggregated social connectivity ki, number of created ties nα,i and number of deleted ties nω,i at t = T, compared with the pdf for the average communication capacity  over the observation window. (B) Relationship between the number of formed nα,i and decayed nω,i ties in the observation window for the users in our database: the results form the PCA indicate that the 93% of the variation can be explained by the first component in the (0.70, 0.71) direction, i.e. almost the black line nα,i = nω,i in the plot. Furthermore, the box plot shows the 25% and 75% percentiles (filled box) and 5% and 95% percentiles (whiskers) and the blue curves correspond to the 5% and 95% percentiles of the corresponding Poisson null model for our data (see
Supplementary Section 5
). (C) Density plot ρ(log ωi, log αi) for users with more than 5 ties formed and decayed. Dashed line is the αi = ωi relationship and the curves correspond to the contour lines ρ = 0.01 for the density of actual values of rates (red) and the ones obtained in the Poissonian null model (blue, see
Supplementary Section 5
for further information).
over the observation window. (B) Relationship between the number of formed nα,i and decayed nω,i ties in the observation window for the users in our database: the results form the PCA indicate that the 93% of the variation can be explained by the first component in the (0.70, 0.71) direction, i.e. almost the black line nα,i = nω,i in the plot. Furthermore, the box plot shows the 25% and 75% percentiles (filled box) and 5% and 95% percentiles (whiskers) and the blue curves correspond to the 5% and 95% percentiles of the corresponding Poisson null model for our data (see
Supplementary Section 5
). (C) Density plot ρ(log ωi, log αi) for users with more than 5 ties formed and decayed. Dashed line is the αi = ωi relationship and the curves correspond to the contour lines ρ = 0.01 for the density of actual values of rates (red) and the ones obtained in the Poissonian null model (blue, see
Supplementary Section 5
for further information).
The imbalance between the number of activated and deactivated ties measures how communication capacity changes. At the end of the observation period the change is κi(T) − κi(0) = nα,i(T) − ni,ω(T). Interestingly, we find that for most users in our database we get  (see details in Fig. 3b). This means that there is a conservation principle in social communication, where the number of deactivated ties equals the number of activated ties in our observation window Ω such that the total number of active ties remains almost constant after T = 7 months. This conservation of communication capacity not only happens at this particular time scale T but also instantaneously: as seen in Fig. 2c for a particular user (and
SI Section 3
) we find that for around 90% of the users tie activation/deactivation happens linearly in time so that
(see details in Fig. 3b). This means that there is a conservation principle in social communication, where the number of deactivated ties equals the number of activated ties in our observation window Ω such that the total number of active ties remains almost constant after T = 7 months. This conservation of communication capacity not only happens at this particular time scale T but also instantaneously: as seen in Fig. 2c for a particular user (and
SI Section 3
) we find that for around 90% of the users tie activation/deactivation happens linearly in time so that  and
and  , where αi and ωi are the rates of tie activation/deactivation and
, where αi and ωi are the rates of tie activation/deactivation and  (see Fig. 3c and
SI Section 4
). These two facts have a remarkable consequence: despite ties are activated/deactivated continually, the communication capacity for each individual remains almost constant throughout the observation period
(see Fig. 3c and
SI Section 4
). These two facts have a remarkable consequence: despite ties are activated/deactivated continually, the communication capacity for each individual remains almost constant throughout the observation period  , signaling that people tend to balance the activation/deactivation of ties in such a way that the number of active relationships remains stable over time. The conservation of social capacity is the root of many observations in the literature (see for example4,24) that the distribution of connectivity in social networks seems to be stable in time but the neighbors of a given node change from one time window to another one. Specifically, we find that the average user social persistence pi, measured as the fraction of neighbors present at the beginning of the observation window Ω that remain active until its end, lies around 75%. This means that users renew their social circle slowly, in line with studies in off-line social networks2. This value is much larger than what is expected in a model where all ties have the same probability to be activated or deactivated, in which case we obtain
, signaling that people tend to balance the activation/deactivation of ties in such a way that the number of active relationships remains stable over time. The conservation of social capacity is the root of many observations in the literature (see for example4,24) that the distribution of connectivity in social networks seems to be stable in time but the neighbors of a given node change from one time window to another one. Specifically, we find that the average user social persistence pi, measured as the fraction of neighbors present at the beginning of the observation window Ω that remain active until its end, lies around 75%. This means that users renew their social circle slowly, in line with studies in off-line social networks2. This value is much larger than what is expected in a model where all ties have the same probability to be activated or deactivated, in which case we obtain  (see
SI Section 5
). Our results corroborates that the way in which people activate and deactivate ties from their social network is not random; instead, some existing ties are more probable to be deactivated than others.
(see
SI Section 5
). Our results corroborates that the way in which people activate and deactivate ties from their social network is not random; instead, some existing ties are more probable to be deactivated than others.
Thus, individual communication can be characterized in terms of his communication capacity  and his communication activity nα,i (or rate αi) in a time window. These two quantities give information about two related although not equivalent features of social communication. While the capacity is a measure of the number of relations that a user manages instantaneously, the activity is instead related to the number of relations a user establishes and at what rate. However, as shown in Fig. 4, we observe for a large part of the individuals that
and his communication activity nα,i (or rate αi) in a time window. These two quantities give information about two related although not equivalent features of social communication. While the capacity is a measure of the number of relations that a user manages instantaneously, the activity is instead related to the number of relations a user establishes and at what rate. However, as shown in Fig. 4, we observe for a large part of the individuals that  with β = 0.75, meaning that the number of created connections tends to be proportional to the communication capacity. This correlation resembles the preferential attachment process by which tie activation is more probable for more connected individuals. Note however that we find that tie activation is here proportional to a conserved quantity and thus grows linearly in time for
with β = 0.75, meaning that the number of created connections tends to be proportional to the communication capacity. This correlation resembles the preferential attachment process by which tie activation is more probable for more connected individuals. Note however that we find that tie activation is here proportional to a conserved quantity and thus grows linearly in time for  ; and on top of that, there is a corresponding preferential de-attachment mechanism meaning that individuals with large
; and on top of that, there is a corresponding preferential de-attachment mechanism meaning that individuals with large  are also more likely to deactivate ties. Although the dependence
are also more likely to deactivate ties. Although the dependence  explains most of the observed behavior (80% of variance in PCA), there is a still a large variability in our database so that tie evolution cannot be explained solely by
explains most of the observed behavior (80% of variance in PCA), there is a still a large variability in our database so that tie evolution cannot be explained solely by  . As shown in Fig. 3, for a given number of people contacted in the observation period ki(T) there are many possible combinations of social activity nα,i and capacity
. As shown in Fig. 3, for a given number of people contacted in the observation period ki(T) there are many possible combinations of social activity nα,i and capacity  which yield to the same ki(T).
which yield to the same ki(T).
Variability of communication capacity and activity.
(A) and (B) show different snapshots of the neighborhood of two different individuals (in red) at 4 equally spaced times in the observation time window t = 52, 105, 158 and 211 days. Each black (grey) line corresponds to an active (inactive) tie at that particular instant. (C) Log-density plot of the communication activity nα,i as a function of the communication capacity κi for each individual in our database. Solid line corresponds to the line  obtained through PCA. Dashed curves are the iso-connectivity lines
obtained through PCA. Dashed curves are the iso-connectivity lines  for ki = 10, 20, 50.
for ki = 10, 20, 50.
Lifetime evolution and sex differences
Although the communication capacity and activity remain mostly stable over the observation time window Ω, they tend to change gradually during the individual life course. Specifically, as shown in Fig. 5, we observe that as people get older the size of their social circle (ki = nα,i + κi) decreases. This decrease in both the communication capacity and activity observed in Fig. 5 is in line with previous studies on the lifetime evolution of the cognitive and communication capacity of individuals25,26,27. Specifically, changes in egocentric network size across the individual lifespan are usually associated to both experiencing age-specific life events and social goals28. Other studies relate the decrease in the social engagement (number of social contacts, interaction activity, frequency of communication) across the individual lifespan, to a decrease in the cognitive capacity27,28,29,30. Our decomposition of ki as a combination of nα and κi allows us to better understand the change in social network size across the individual lifespan and its relation with individual communication strategies.
Sociodemographic dependence of the capacity and activity.
(A) Average value of the social capacity  and the activity
and the activity  for groups of users with different age and gender. Dashed lines correspond to the average of κi and nα,i in the complete database and the solid line is the line nα,i = βκi obtained through the PCA in the complete database. (B) Average values for the activity and capacity of users grouped by gender.
for groups of users with different age and gender. Dashed lines correspond to the average of κi and nα,i in the complete database and the solid line is the line nα,i = βκi obtained through the PCA in the complete database. (B) Average values for the activity and capacity of users grouped by gender.
Although the trend in vital trajectories does not change significantly with the gender of the individual, interesting differences are observed between men and women social strategies (Fig. 5). First, in line with recent studies using mobile phone records31,43, we found that on average women maintain smaller social circles than men, which seem to happen regardless to their age. Interestingly, communication activity and capacity have a gradual change over the lifetime of men, with no significant drop before the 60 s. On the other hand, women have a clearly marked difference between adolescence (<16 years) and the rest of their lifetime.
Social strategy
As we show in Fig. 4, there are many different combinations of communication capacity  and activity nα,i which yield to the same number of tie activations/deactivations in the observation window ki. We encode that disparity in the ratio
and activity nα,i which yield to the same number of tie activations/deactivations in the observation window ki. We encode that disparity in the ratio  which we dub as social strategy and gives information about the balance between the communication capacity and the communication activity for a given node: for
which we dub as social strategy and gives information about the balance between the communication capacity and the communication activity for a given node: for  (the average behavior), users have a normal or balanced social strategy between their communication capacity and activity. Outside this group we find those users with
(the average behavior), users have a normal or balanced social strategy between their communication capacity and activity. Outside this group we find those users with  that activate/deactivate a small number of connections compared to their communication capacity, or users with
that activate/deactivate a small number of connections compared to their communication capacity, or users with  who have a large communication activity compared to their communication capacity. We refer to these two strategies as social keeping (
who have a large communication activity compared to their communication capacity. We refer to these two strategies as social keeping ( ), meaning that these individuals keep a very stable social circle and social exploring (
), meaning that these individuals keep a very stable social circle and social exploring ( ), meaning that these individuals activate new ties and deactivate existing ones at a high pace.
), meaning that these individuals activate new ties and deactivate existing ones at a high pace.
In the following we study how such different social strategies relate to topological properties and impact the local and global network dynamics as they operate in the time-scales relevant for viral information diffusion.
Relation to topological properties
We find a significant correspondence between social strategy and individuals' local network topology. As mentioned above, users show on average a 75% persistence in their ties in 7 months, where the persistence is measured as the fraction of initial ties that remain active during the whole Ω (see SI Section F ). However, as shown in the SI Section F this value rises up to 90% for social keepers with γi < 0.2 and is only 52% for social explorers with γi > 2. A similar dependency is found for the (aggregated) clustering coefficient ci: as shown in the SI Section F for a fixed ki, the clustering coefficient for social keepers doubles that of social explorers, meaning that for equal ki the former have less distinct social contexts or structural diversity34 than the latter. Finally, we find that along with the assortativity of ki in the social networks we get a large assortativity of social strategies with a Pearson coefficient ρ(γi, γnn,i) ~ 0.3 (see SI Section 6 for further details). This means that social explorers/keepers tend to gather. These findings render a dynamical picture of the network with very different evolution rhythms: highly clusterized and almost static areas of social keepers live together with extremely volatile groups of social explorers.
Our analysis of the Facebook communication dataset shows that these patterns also hold for users interacting online (see SI Section 7 ).
Information diffusion
Finally we investigate whether social strategies have an impact in an individual's capacity to access information being propagated in a network. To address this, we have run the Susceptible-Infected model on the real sequence of CDRs. In a way analogous to previous works32,33, we start the simulation by infecting a random node at a random time instant and considering all other nodes as susceptible. At each call, if either involved nodes is infected, the susceptible one will be infected too. This maximal spreading process generates a viral cascade which continues until all reachable nodes are in the infected state. We repeat the simulation for 104 randomly chosen seeds. For each individual we then measure the infection time tinf as the time difference between the time at which she received the information and the time at which the corresponding cascade was initiated. Obviously, for a given individual, the infection time decreases with her total connectivity ki and the total number of communication events wi: the more connections an individual has and the more she interacts, the sooner she receives the information. But when we control for ki and wi, we observe that on average there is a dependence between how stable the social strategy is and the infection time (see Fig. 6b). Interestingly, we observe that social explorers (γi > 2) have a relatively larger infection time (roughly 2–3 days of difference) compared to social keepers (γi < 0.2).
Infection time and social strategies.
(A) Relation between average infection time and γi for the different connectivity groups ki = 10, 20, 50 (the Pearson coefficient between tinf and log(γi) is 0.13 with confidence range [0.12,0.14]).(B) For the connectivity group ki = 20 we show the dependence of the average infection time on the total number of exchanged calls wi and the social strategy γi.
We observe that only some combinations of node strength and social strategy are possible. With low to moderate levels of exploration in social strategies ( ) it is possible to reach a wide range of node strengths, with a sweet spot in connectivity that allows individuals to lower their time to access information. However, with
) it is possible to reach a wide range of node strengths, with a sweet spot in connectivity that allows individuals to lower their time to access information. However, with  the number of nodes with high strength decreases exponentially: highly exploratory individuals display a very low level of communication events and therefore a very large time to receive information circulating in the network. This result suggests that the information access benefits of diverse ties are outweighted by their short time lifespan, resulting in a net delay in access to information from the individuals activating them.
the number of nodes with high strength decreases exponentially: highly exploratory individuals display a very low level of communication events and therefore a very large time to receive information circulating in the network. This result suggests that the information access benefits of diverse ties are outweighted by their short time lifespan, resulting in a net delay in access to information from the individuals activating them.
Discussion
Our insights can be seen, in essence, as the individual-level dynamical version of the tie-level static results reported by Onnela et al.22. The authors analyzed 18 weeks of mobile phone call records from 7 million people and showed that, in terms of information diffusion, ties with low cumulative communication time (strength in our context) are ineffective at information transfer. Our results clarify that these ties are disproportionally generated by social explorers and that they are mostly activated and deactivated in a short time span. In fact, we find that the average tie weight of each individual  (measured in terms of average number of exchanged calls per tie) is negatively correlated to the social strategy γi with a Pearson coefficient
(measured in terms of average number of exchanged calls per tie) is negatively correlated to the social strategy γi with a Pearson coefficient  , indicating that on average weak ties belong mostly to social explorers. Note that these highly time-localized communications differ from the conventional wisdom about weak ties. Typically, in fact, weak ties are seen as bridging connections that span remote parts of the network permanently, since they are considered active over the whole observation period36,37,38,39. In our dataset, instead, this happens with low frequency. Although a detailed analysis of what constitutes a weak ties is beyond our scope, we find that of all ties with less than 10 calls (corresponding to 50% of the whole population of ties), only almost 20% of them remain active during the entire observation window. This is also consistent with the ”Diversity-Bandwidth Tradeoffs” observed in corporate email communication datasets from two medium sized firms (107 people over 10 months; 214 over 12 months). The authors found empirical evidence that people who form ties to disparate parts of the social network at the cost of reducing their band-width of communication can have disadvantaged access to novelty they receive40,41. Our simulation results support this result for a large scale social network and connect it to measurable individual strategies.
, indicating that on average weak ties belong mostly to social explorers. Note that these highly time-localized communications differ from the conventional wisdom about weak ties. Typically, in fact, weak ties are seen as bridging connections that span remote parts of the network permanently, since they are considered active over the whole observation period36,37,38,39. In our dataset, instead, this happens with low frequency. Although a detailed analysis of what constitutes a weak ties is beyond our scope, we find that of all ties with less than 10 calls (corresponding to 50% of the whole population of ties), only almost 20% of them remain active during the entire observation window. This is also consistent with the ”Diversity-Bandwidth Tradeoffs” observed in corporate email communication datasets from two medium sized firms (107 people over 10 months; 214 over 12 months). The authors found empirical evidence that people who form ties to disparate parts of the social network at the cost of reducing their band-width of communication can have disadvantaged access to novelty they receive40,41. Our simulation results support this result for a large scale social network and connect it to measurable individual strategies.
Although, as we have seen, the adoption of social strategies does not seem to depend on the magnitude of activity and capacity, we have found them to be assortative. In addition, despite we cannot establish causality with our methodology and observational period, it is an interesting question whether social strategies can be behind the homophily in static topological properties, which has been observed in a wide range of real social networks35.
These findings document an important contrast between possible social dynamics: for almost any given ki we can find social explorers with that connectivity that navigate the network for new ties and thus have larger structural diversity, as well as social keepers, more conservative individuals who focus attention to their stable social neighborhood. In other words, individuals can exhibit exploratory or stable strategies at multiple scales of connectivity and these strategies have more important impact in the resulting network properties, ranging from cohesiveness to information diffusion, that the total number of contacts they are able to initiative or receive. This result is important as it provides conclusive evidence for the divergence between the static and dynamic characterizations human interaction. Fine-grained, longitudinal and cross-sectional data as the one presented in this study are then needed to fully understand processes such as navigation, influence and information diffusion as they happen concurrently and possibly entangled to the unfolding of social strategies in time.
Methods
We consider a large mobile phone communication database and for the sake of comparison a small (although rather long) communication database through wall posts in Facebook44. We refer the reader to the SI for the details and analysis on the Facebook data.
Mobile phone data
The data used in this study has been obtained from the Call Detail Records database of a unique mobile phone operator in a single country. We focused exclusively on voice calls records, filtering out short text messages, multimedia messages and operator calls. Each subscription is anonymized such that it is not possible to recover personal information of the users. We filtered out all the incoming or outgoing calls that involve other operators due to the partial access we have to the activity of other providers. To avoid business-like subscriptions, which usually appear as users with a huge number of connections and calls never returned, we only retain ties which are reciprocated, which leads to the removal of about the 50% of the total links in our database. This restriction also eliminates calls to wrong numbers, telemarketing-type calls, customer service lines, etc. Within this approach, we neglect the directionality of links and consider a call from i to j equivalent to a call from j to i22. The resulting mobile graph contains the communication of about 20 × 106 users over a period of 19 months from February 2009 to August 2010.
Data filtering
To disentangle the dynamics of ties creation/removal from their call activity, we split the 19-months period into 3 subintervals (Feb09 - Jul09, Aug09 - Feb10, Mar10 - Aug10), (see Fig. 1). We have only considered the evolution of the ties and nodes that show any activity in the 7 months observation window Ω (Aug09 - Feb10). The resulting graph in Ω contains 16 × 106 individuals and 130 × 106 ties. The intervals before and after are used to assess respectively whether the ties exist from before and/or persist after Ω. Fig. 1 shows the different situations that can occur for a given tie. In particular, in our database, the 12.5% of links belongs to the category (a), the 14.5% to (b), the 22.2% to (c) and the 47.3% to (d), while only the 3.5% of the links, which belong to category (e), will be missed in our analysis.
Since we are interested only in tie dynamics between individuals, we have to take into account the problem of subscription and churn of users in our database. For example, subscription of a new user and its communication with other users in our database results into formation of many new ties for the new subscriber. The same would happen for the decay of ties of a subscribe that churns from the company. To mitigate this problem, we only keep active users in our data set: in particular, we only consider those users who are involved (as calling or as called party) at least in one communication event in each of the three subintervals in the 19 months and also if they are present in the database at least one month before Ω and are still active one month after Ω. This latter filter prevents spurious effects in the analysis of tie dynamics just because individuals subscribe/unsubscribe just before/after Ω; for example, we could have observed an apparent rapid growth of their social network at the beginning of the observation window or a fast dissolution at its end45. This results in the removal of about the 17% of nodes and the 37% of reciprocated links within Ω.
Finally, we would like to notice that although our database contains a large fraction of mobile users in the country under consideration, there could be a potential bias in the population sampled, in common with other studies reliant on mobile phone networks4,5,22,23,31,32,33,37,42. However, since we obtain similar results also for the Facebook database, we are confident that our main findings are not affected by a potential sample bias.
Other information
In our database, we also have information on the age and gender of users of a random fraction (40%) of them. This dataset contains approximately the 35% of female and 65% of male users, while the age distribution has a significant higher mass in users between 20 and 60 than the country population, with a peak around 25 years old. Nevertheless, our analysis is performed for different groups of age/gender population, thus it is reasonable to assume that this sample bias does not affect the observed outcomes. The minimum and maximum values of age are respectively 0 and 97. However, we only keep users whose age lies between 16 and 70 years old in order to yield a more reliable dataset. This filtering led to the removal of the 0.5% of users which demographic data.
References
Rivera, M. T., Soderstrom, S. B. & Uzzi, B. Dynamics of Dyads in Social Networks: Assortative, Relational and Proximity Mechanisms. Annual Review of Sociology 36, pp. 91–115 (2010).
Burt, R. S. Deactivation functions. Social Networks 22, 1–28 (2000).
Martin, J. L. & Yeung, K.-T. Persistence of close personal ties over a 12-year period. Social Networks 28, 331–362 (2006).
Hidalgo, C. H. & Rodriguez-Sickert, C. The dynamics of a mobile phone network. Physica A 387, 3017–3024 (2008).
Raeder, T., Lizardo Chawla, N. V. & Hachen, D. Predictors of short-term deactivation of cell phone contacts in a large scale communication network. Social Networks 33, 245–257 (2011).
Kossinets, G. & Watts, D. J. Origins of homophily in an evolving social network. American Journal of Sociology 115, 405–450 (2009).
Crandall, D., Cosley, D., Huttenlocher, D., Kleinberg, J. & Suri, S. Feedback effects between similarity and social influence in online communities. In KDD'08: Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NY, USA, ACM pp. 160–168 (2008).
Romero, D. M., Meeder, B., Barash, V. & Kleinberg, J. Maintaining Ties on Social Media Sites: The Competing Effect of Balance, Exchange and Betweenness. Proceedings of ICWSM 2011: the fifth AAAI conference on Weblogs and Social Media, Barcelona, Spain (2011).
Wang, J., Suri, S. & Watts, D. J. Cooperation and assortativity with dynamic partner updating. Proc. Natl. Acad. Sci. USA 109, 14363–14368 (2012).
Apicella, C. L., Marlowe, F. W., Fowler, J. H. & Christakis, N. A. Social networks and cooperation in hunter-gatherers. Nature 481, 497–501 (2012).
Rand, D. G., Arbesman, S. & Christakis, N. A. Dynamic social networks promote cooperation in experiments with humans. Proc. Natl. Acad. Sci. USA, 108, 19193–19198 (2012).
Wu, F. & Huberman, B. A. Novelty and collective attention. Proc. Natl. Acad. Sci. USA 104, 17599–17601 (2007).
Hodas, N. O. & Lerman, K. How visibility and divided attention constrain social contagion. In 2012 International conference on Privacy, Security, Risk and Trust (PASSAT) and 2012 International Conference on Social Computing (SocialCom)., IEEE pp. 249–257 (2012).
Backstrom, L., Bakshy, E., Kleinberg, J., Lento, T. M. & Rosenn, I. Center of attention: How facebook users allocate attention across friends. Proc. 5th International Conference on Weblogs and Social Media (2011).
Hagerstrand, T. Innovation diffusion as a spatial process (Univ. Chicago Press., Chicago, USA) (1968).
Rogers, E. M. Diffusion of Innovations (Free Press, New York 1995).
Christakis, N. A. & Fowler, J. H. The spread of obesity in a large social network over 32 years. The New England journal of medicine 357, 370–379 (2007).
Huberman, B. A., Romero, D. M. & Wu, F. Social networks that matter: Twitter under microscope. First Monday 14, 1 (2009).
Grabowicz, P. A., Ramasco, J. J., Moro, E., Pujol, J. M. & Eguíluz, V. M. Social features of online networks: the strength of weak ties in online social media. PLoS ONE 7, e29358 (2011).
Sibona, C. & Walczak, S. Unfriending on Facebook: Friend request and online/offline behavior analysis. Proceedings of the 44th Hawaii International Conference on System Sciences (HICSS) pp. 1–10 (2011).
Barabási, A.-L. The origin of bursts and heavy tails in human dynamics. Nature 435, 207–211 (2005).
Onnela, J.-P. et al. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 104, 7332–7336 (2007).
Krings, G., Karsai, M., Bernharsson, S., Blondel, V. D. & Saramäki, J. Effects of time window size and placement on the structure of aggregated networks. EPJ Data Science 1, 4 (2012).
Kossinets, G. & Watts, D. Empirical analysis of an evolving social network. Science 311, 88–90 (2006).
Tilburg, T. G. Losing and Gaining in Old Age: Changes in Personal Network Size and Social. Support in a Four-Year Longitudinal Study. Journal of Gerontology: Social Sciences 53B, S313–S323 (1998).
Kahn, R. L. & Antonucci, T. C. Convoys over the life course: attachment, roles and social support., in Life-span Development and Behavior Baltes, P., Brim, O., eds., pp. 253–286 (Academic Press, New York, 1980).
Seeman, T. et al. Histories of social engagement and adult cognition in middle and late life: the midlife in the US study. Journal of Gerontology: Psychological Sciences, 66B, i141–i152 (2011).
Wrzus, C., Hänel, M., Wagner, J. & Neyer, F. J. Social Network Changes and Life Events Across the Life Span: A Meta-Analysis. Psychological Bulletin 139, 53–80 (2013).
Carstensen, L. L., Isaacowitz, D. M. & Charles, S. T. Taking time seriously: A theory of socioemotional selectivity. American Psychologist 54, 165–181 (1999).
Carstensen, L. L. Socioemotional selectivity theory: social activity in life-span context. Annual Review of Gerontology and Geriatrics 11, 195–217 (1991).
Frías-Martinez, V., Frías-Martinez, E. & Oliver, N. A Gender-centric Analysis of Calling Behavior in a Developing Economy Using Call Detail Records. Proceedings of AAAI Artificial Intelligence for Development (2010).
Miritello, G., Moro, E. & Lara, R. Dynamical strength of social ties in information spreading. Phys. Rev. E 83, 045102 (2011).
Karsai, M. et al. Small But Slow World: How Network Topology and Burstiness Slow Down Spreading. Phys. Rev. E 83, 025102 (2011).
Ugander, J., Backstrom, L., Marlow, C. & Kleinberg, J. Structural Diversity in Social Contagion. Proc. Natl. Acad. Sci. USA 109, 5962–5966 (2012).
Newman, M. E. J. Assortative mixing in networks. Phys. Rev. Lett. 89, 208701 (2002)
Granovetter, M. The Strength of Weak Ties. American Journal of Sociology 78, 1360–1380 (1973).
Eagle, N., Macy, M. & Claxton, R. Network diversity and economic development. Science 328, 1029–1031 (2010).
Centola, D. & Macy, M. Complex contagions and the weakness of long ties. American Journal of Sociology 113, 702–734 (2007).
Centola, D. The spread of behavior in an online social network experiment. Science 329, 1194–1197 (2010).
Aral, S. & Van Alstyne, M. The Diversity-Bandwidth Trade-off. American Journal of Sociology 117, 90–171 (2011).
Aral, S. & David, V. The Anatomy and Dynamics of Vision Advantages. Proceedings of the 33rd International Conference on Information Systems (2012).
Song, C., Wang, D. & Barabasi, A.-L. Joint Scaling Theory of Human Dynamics and Network Science. arXiv:1209.1411v1 (2012).
Palchykov, V. et al. Sex differences in intimate relationships. Scientific Reports 2, 370 (2012).
Viswanath, B. et al. On the evolution of user interaction in facebook. Proceedings of the 2nd ACM workshop on Online social networks pp. 37–42 (2009).
Gaito, S., Zignani, M., Rossi, G. P., Sala, A., Zhao, X., Zheng, H. & Zhao, B. Y. On the bursty evolution of online social networks. In Proceedings of the First ACM International Workshop on Hot Topics on Interdisciplinary Social Networks Research,. ACM pp. 1–8, arXiv:1203.6744v1 (2012).
Acknowledgements
We would like to thank Telefónica for providing access to the anonymized data. E.M. and G.M. acknowledge funding from Ministerio de Educación y Ciencia (Spain) through projects i-Math, FIS2006-01485 (MOSAICO) and FIS2010-22047-C05-04. M.C. acknowledges support from the National Science Foundation under grant 0905645, from DARPA/Lockheed Martin Guard Dog Program PO# 4100149822 and the Army Research Office under Grant W911NF-11-1-0363.
Author information
Authors and Affiliations
Contributions
G.M., R.L., M.C. and E.M. designed research; G.M. and E.M. analyzed the data. All authors wrote, reviewed and approved the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Miritello, G., Lara, R., Cebrian, M. et al. Limited communication capacity unveils strategies for human interaction. Sci Rep 3, 1950 (2013). https://doi.org/10.1038/srep01950
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01950
This article is cited by
-
The stability of transient relationships
Scientific Reports (2023)
-
Micro-level social structures and the success of COVID-19 national policies
Nature Computational Science (2022)
-
Turnover in close friendships
Scientific Reports (2022)
-
Communication now and then: analyzing the Republic of Letters as a communication network
Applied Network Science (2022)
-
The network limits of infectious disease control via occupation-based targeting
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.