Abstract
We have developed an algorithm for recording multiple gradated two-dimensional projection patterns in a single three-dimensional object. When a single pattern is observed, information from the other patterns can be treated as background noise. The proposed algorithm has two important features: the number of patterns that can be recorded is theoretically infinite and no meaningful information can be seen outside of the projection directions. We confirmed the effectiveness of the proposed algorithm by performing numerical simulations of two laser crystals: an octagonal prism that contained four patterns in four projection directions and a dodecahedron that contained six patterns in six directions. We also fabricated and demonstrated an actual prototype laser crystal from a glass cube engraved by a laser beam. This algorithm has applications in various fields, including media art, digital signage and encryption technology.
Similar content being viewed by others
Introduction
The image projected by a three-dimensional object varies depending on the projection method and the angle of the projection axis. Figure 1 shows that a single central object can project three distinct patterns, the characters “X”, “Y” and “Z”. In this example, parallel projection is used and the three projection axes are mutually orthogonal. A similar object that contains the projection patterns of the characters “G”, “E” and “B” is depicted on the cover of the book, “Gödel, Escher, Bach: An Eternal Golden Braid”1. We see, therefore, that three two-dimensional information patterns can be recorded in a single three-dimensional object. Multiple patterns can be thus recorded in a three-dimensional object by solving the relevant eigenvalue problems. It is possible to project different binarized images on three axes by this technique2. However, the combination and the number of patterns that can be recorded are limited and each pattern is a binarized image. For example, this method cannot record the combination of characters “I”, “I” and “I” in a single three-dimensional object.
The algorithm proposed in this paper allows any number of patterns and almost any pattern to be recorded in a single three-dimensional object. The most significant characteristic of this algorithm is that the projection patterns are not required to be binary, but are allowed to have gradation. A projected pattern is recognizable because its signal is stronger than the extraneous information, which is treated as background noise.
Results
Numerical simulation
We performed computer simulations for two laser crystals: an octagonal prism with four patterns and four projection axes and a regular dodecahedron with six patterns and six projection axes. Each pattern consisted of 64 × 64 pixels and the voxel values were given by the crack density at each point. In the prism, the volume included a total of 493,169 cracks and for the dodecahedron it was 494,464. In both cases, we determined that no meaningful information could be seen outside of the projection directions, i.e., when the object was viewed from an angle that was not in line with a projection axis. Also, in both cases, although the projected patterns were a little noisy, nevertheless, they were quite recognizable as the intended patterns.
Figure 2 shows the results of a computer simulation for a laser crystal made from an octagonal prism with four projection axes. Figure 2(a) shows the prism from an angle that is not in line with a projection axis and this illustrates that no meaningful information can be seen outside of the projection directions. Figure 2(b) shows the four patterns that were used. Figure 2(c)) shows the patterns that were reconstructed by projections from the volume. Figure 2(d) shows the results of a computer simulation for a laser crystal made from a regular dodecahedron with six projection axes. Figure 2(e) shows the dodecahedron from an angle that is not in line with a projection axis. Figure 2(f) shows the six patterns that were used. Figure 2(g) shows the patterns that were reconstructed by projections from the volume.
Computer simulations for two laser crystals (three-dimensional glasslike volumes): an octagonal prism with four patterns and four projection axes and a regular dodecahedron with six patterns and six projection axes.
(a) View of the octagonal prism from an angle that is not in line with a projection axis. (b) Four original patterns, each consisting of 64 × 64 pixels. (c) Four images reconstructed by the octagonal prism and obtained from views normal to the direction of the surface. (d) View of the regular dodecahedron from an angle that is not in line with a projection axis. (e) Six original patterns, each consisting of 64 × 64 pixels. (f) Six images reconstructed by the regular dodecahedron and obtained from views normal to the direction to the surface.
The images used in the simulations were original and the pictures which were from a standard test image database.
Prototype of a three-dimensional laser crystal
Figure 3 shows the actual prototype of cubic three-dimensional laser crystal with three projection axes. Figure 3(a) is the view from an angle not in line with a projection axis. We can observe no meaningful information outside the appropriate axis direction. Figure 3(b) presents the three original patterns, each of which consists of 64 × 64 pixels. Figure 3(c) shows the photographs obtained from views normal to the surface. The cubic laser crystal has side of 6 cm and contains 492,719 cracks. The patterns are recognizable as the original pattern. Note that this is an example of a volumetric display3,4.
Cubic three-dimensional prototype laser crystal with three projection axes, sides of 6 cm.
(a) View of the three-dimensional laser crystal from a direction not in line with a projection axis. (b) Original patterns, each consisting of 64 × 64 pixels. (c) Photographs of images reconstructed by the laser crystal and obtained from directions normal to the surface. (This is linked to the accompanying animation.)
Discussion
We developed an algorithm for recording multiple two-dimensional projection patterns in a single three-dimensional object, although work still needs to be done to improve the quality of the resulting images. We have already begun this work. Specifically, we have added steps to the proposed algorithm for both preprocessing and postprocessing the images. The most important information is usually in the centre of the screen. Although it is desirable that the background noise be uniformly random, irregularities will occur in practice. In the preprocessing step, we make the noise distribution uniform in the centre of the image by sacrificing the quality at the edges. First, we calculate the volume containing multiple two-dimensional patterns. Secondly, we rearrange the pixel values in each reconstructed pattern so that each pattern becomes clearer in the centre at the expense of clarity at the edges. Then, we calculate the volume again. In the postprocessing step, the noise signals are overlapped in the direction of the axes. Each voxel value is obtained from the density of points in the laser crystal. In the original algorithm, the points are placed at random in each voxel. In the postprocessing step, we rearranged the points within the voxel so that the noise points are lined up with the projected pattern. By applying these steps, the peak signal-to-noise ratio (PSNR) improved from 10 dB to 30 dB.
We think that this technology is applicable to digital signage5. Since computerization is important if this is to be used as a display system, we have also developed some electronic systems that make use of the proposed algorithm. One is a cubic display consisting of full-colour light-emitting diodes (LEDs) in an 8 × 8 × 8 array. Figure 4(a) shows the system from a view that is not in line with an axis and thus there is no recognizable pattern information. However, from the front view of the system shown in Fig. 4(b), we observe “20” and “13” (this year is 2013) can be seen in the side view shown in Fig. 4(c). We made another volumetric display system, this one based on a 7 × 7 array of threads6, in which a laser illuminates each thread. Figure 4(d) shows the system from a view that is not in line with an axis. Figure 4(e) shows the front view and Fig. 4(f) shows the side view.
An electronic display system such as this can project an image in any direction and the proposed algorithm limits the range in which the image is seen. In other words, it can determine the direction in which the image is projected. Using this property, it is possible to send visual information to only one specific person. As shown in Fig. 5, the system can track a specific person and project information that will be visible only in that direction. The proposed algorithm allows this to be done for multiple people and multiple images. In practice, this may work in situations where movement is controlled, e.g., airplanes, escalators, moving sidewalks, or trains.
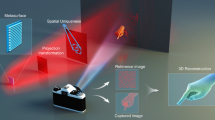
Our method can also be used for encryption. Here, the most important feature of the proposed algorithm is that we cannot recognize meaningful images when we observe the volume from other than the image-projection axes. To take advantage of this feature, we have applied the proposed algorithm to double-random-phase optical encryption7. Figure 6 shows the proposed encryption system that includes our algorithm. In the typical double-random-phase approach, the input image is two dimensional. However, we can regard the laser crystal as a point cloud and instead of a two-dimensional image, we use the proposed algorithm to record images at random positions and at a random angle on the laser crystal. We treat as keys the position and angle of the image on the laser crystal/point cloud. In this way, we have a system that is more secure than the typical double-random-phase approach.
This proposed algorithm can expect to find applications in many fields, including media art, digital signage and encryption technology. In the near future, we hope to report further developments in the applications mentioned above.
Methods
One volume containing three patterns
We begin by describing the method for recording three projection patterns, as shown in Fig. 7. In Fig. 7(a), we see that three original patterns, A, B and C, are located on different axes and are incorporated in a single three-dimensional object. The patterns can be obtained as images in, for example, a bitmap image file (BMP format). The parameters aij, bjk and cki are the pixel values of the respective patterns. The recording space consists of P × Q × R voxels. The blue lines in Fig. 7(b) represent lines from the voxel centre perpendicular to the original patterns. Each voxel value V is defined by

where λ is a constant used to adjust the total intensity. Three original patterns are recorded by calculating all the voxel values in the volume. The densities of the projected patterns from the volume constructed by equation (1) can be represented by



The values in parentheses are changed by varying the indices i, j and k in the above equations. When the changes of the values in parentheses are relatively uniform, they can be treated as constants on the level of perception. Thus, the projected patterns are recognizable as the original patterns due to visual processing in the brain that compresses the image by removing high-frequency components8.
A concrete way of calculating of λ is explained with the aid of Fig. 7(c). Suppose there are three pictures, A, B and C, each of which consist of four pixels. The numbers in the figure show the pixel value of each picture. The values of Aij, Bjk and Cki are then calculated as follows from equations (2) to












When  , the image of aij is in agreement with the original picture. However, it is difficult to obtain a value of λ for which
, the image of aij is in agreement with the original picture. However, it is difficult to obtain a value of λ for which  for all i and j. Thus, instead, λ is set to the reciprocal of the average of all the pixel values. Consequently, the variation in the pixel values is decreased and the high-frequencies can be deleted. The value of λ in this example is as follows:
for all i and j. Thus, instead, λ is set to the reciprocal of the average of all the pixel values. Consequently, the variation in the pixel values is decreased and the high-frequencies can be deleted. The value of λ in this example is as follows:

One volume containing N patterns
The above algorithm can be easily extended to N dimensions  . The green lines in Fig. 8 represent projection axes. If the projection axes are not parallel, the original patterns
. The green lines in Fig. 8 represent projection axes. If the projection axes are not parallel, the original patterns  are recorded in the central volume consisting of voxels. As there are an infinite number of nonparallel axes, in principle, it is possible to record an infinite number of original patterns.
are recorded in the central volume consisting of voxels. As there are an infinite number of nonparallel axes, in principle, it is possible to record an infinite number of original patterns.
As in the general case, the value of each voxel V is defined by

where  represent the pixel values of the points at which lines from the voxel centre perpendicularly intersect the original patterns. As above, λ is a constant used to adjust the total intensity. The N original patterns are recorded by calculating all the voxel values in the volume.
represent the pixel values of the points at which lines from the voxel centre perpendicularly intersect the original patterns. As above, λ is a constant used to adjust the total intensity. The N original patterns are recorded by calculating all the voxel values in the volume.
As an example, we will consider pattern P(1) (see Fig. 8). The projected pattern density is the summation of the voxel values in the normal direction:

When the values in parentheses in equation (6) are relatively uniform, they can be treated as constants on the level of perception. Thus, the projected patterns are recognizable as the original patterns, just as in the three-dimensional (N = 3) case.
Change history
27 June 2013
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Hofstadter, D. R. Gödel, Escher, Bach: an Eternal Golden Braid. xiv (Basic Books, New York, 1979).
Mitra, N. J. & Pauly, M. Shadow Art. ACM T. Graphic. 28, Article No. 156 (2009).
MacFarlane, D. L. Volumetric three-dimensional display. Appl. Optics 33, 7453–7457 (1994).
Blundell, B. & Schwartz, A. Volumetric Three-Dimensional Display Systems (Wiley-IEEE Press, New Jersey, 1999).
Muller, J. et al. Display Blindness: The Effect of Expectations on Attention towards Digital Signage. Lecture Notes in Computer Science 5538, 1–8 (2009).
Parker, M. Lumarca. ACM SIGGRAPH ASIA 2009. Art Gallery & Emerging Technologies 77 (2009).
Alfalou, A. & Brosseau, C. Optical image compression and encryption methods. Adv. Opt. Photon 1, 589–636 (2009).
Acharya, T. & Ray, A. K. Image processing: principles and applications (Wiley-Interscience, New Jersey, 2005).
Author information
Authors and Affiliations
Contributions
H.N. and T.I. suggested this technique. A.S. and N.M. wrote the main manuscript text. R.H. and T.S. prepared Figs. 4,5,6. All authors reviewed the manuscript.
Two types of electronic volumetric display systems.
(a) A system made of full-colour LEDs seen from a view not in line with an axis. (b) Front view of (a). (c) Side view of (a). (d) A system made of threads seen from a view not in line with an axis. (e) Front view of (d). (f) Side view of (d). (These are linked to the accompanying animations.)
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Nakayama, H., Shiraki, A., Hirayama, R. et al. Three-dimensional volume containing multiple two-dimensional information patterns. Sci Rep 3, 1931 (2013). https://doi.org/10.1038/srep01931
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01931
This article is cited by
-
Survey on computational 3D visual optical art design
Visual Computing for Industry, Biomedicine, and Art (2022)
-
Inkjet printing-based volumetric display projecting multiple full-colour 2D patterns
Scientific Reports (2017)
-
Optical Addressing of Multi-Colour Photochromic Material Mixture for Volumetric Display
Scientific Reports (2016)
-
Aerial projection of three-dimensional motion pictures by electro-holography and parabolic mirrors
Scientific Reports (2015)
-
Design, Implementation and Characterization of a Quantum-Dot-Based Volumetric Display
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

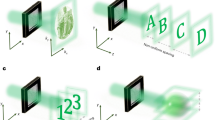





 can be recorded if the projection axes are not parallel.
can be recorded if the projection axes are not parallel.

